中继网络中不准确信道状态信息下抗多窃听者的物理层安全方案

雷维嘉 左莉杰 江 雪 谢显中

1 引言

信息传输的安全性是通信中的重要问题，而无线通信由于传输的开放性使得安全性更为复杂和困难。研究表明，除通过高层的加密外，无线通信中实现信息的安全传输也可在物理层通过物理层安全技术[1]来解决，且系统的安全性可用保密容量[2]、保密中断概率等指标来量化。从信号处理角度，一般通过多发射天线技术，利用无线信道的随机衰落特性获得对合法用户有利的波束赋形来提高物理层安全性能。但前提条件是需要获得各节点间的完整信道状态信息（Channel State Information, CSI）。在许多文献的研究中都假设所有CSI都是已知的[3,4]，这时可以充分利用多天线技术和协作通信技术来改善安全性。文献[3,4]在放大转发（Amplify-and-Forward, AF）中继波束赋形的网络模型下，提出了在总功率或中继功率约束下的增强物理层安全性能的方案，并利用半定松弛方法来解决凸半定规划（Semi-Definite Programs, SDP）问题，获得最优的系统保密速率。然而，在实际中所有CSI都可获得是一种理想情况，因此一些文献也对只能获得部分CSI时的物理层安全问题进行研究。在文献[5]中，给出中继-窃听端的CSI在一定范围具有不确定性的情况下保密速率最大化的设计方案。文献[6]在中继-窃听端的CSI未知的情况下，从用户服务质量的角度提出了一种两阶段的模拟网络编码方案，通过中继加入人工噪声的方法改善了双向中继传输系统的安全性能。

在考虑存在多个窃听者的情况时，一种是认为窃听者之间没有关联，最大保密速率取决于接收信噪比最大的那一个窃听者。另一种是多个窃听者之间可能存在相互勾结的情况。窃听者间的勾结一般指窃听者之间能够交换或者合并它们窃听得到的信息，这样窃听者能获得更多的信息，再经过处理后可提高接收信息速率，相应保密速率会受到更大的影响。文献[7]基于三节点系统模型，讨论存在多个相互勾结的窃听者时的保密通信问题。文献[8,9]假设存在分散的勾结窃听者，其位置分布服从空间泊松过程，在已知全部CSI的情况下，将多个分散的勾结窃听者看作是一个多天线的窃听者。文献[10]在协作无线网络中假设已知全部CSI并且窃听者的位置分布服从齐次泊松过程，中继采用随机转发协议时，对多窃听者勾结的安全性问题进行研究。文献[11]在有多个天线、非勾结窃听者的AF中继网络中，基于窃听端CSI不准确的情况，提出了一个联合协作波束赋形和协作干扰的鲁棒性设计方案，以求得最大保密速率的下界。本文考虑多个单天线窃听者能相互勾结的情况，并将这些相互勾结的单天线窃听者等效为一个多天线的窃听者[7]。由于不易获得窃听者准确的 CSI，本文考虑在仅能获得不准确的窃听者CSI时，在CSI误差最大的情况下保密速率最大化的鲁棒性方案。该方案利用零空间人工噪声和 AF中继波束赋形方法，对中继的波束赋形权值和人工噪声协方差进行联合优化，尽可能地提高信息传输的安全性。

与现有进行类似研究的文献相比，本文工作考虑多个窃听者相互勾结，同时窃听者的CSI不能准确地获得的情况。这两种情况下，物理层安全性的处理和分析都较为困难。现有的文献中，有些考虑了无中继节点的三节点系统模型中窃听者勾结的问题，但假设能获得完整、准确的CSI，如文献[8,9]；有些考虑了中继网络中已知全部CSI情况下窃听者勾结的情况，但没有考虑窃听者的CSI不能准确获得的情况，如文献[10]；有些虽然考虑了CSI不完整或不准确的问题，但没有考虑中继网络中窃听者勾结的问题，如文献[5]。本文研究的模型更符合实际的情况，方法和结论具有更大的实际意义。

本文使用的特殊符号说明如下：dd（A）表示以矩阵A的对角线元素为对角线元素的对角矩阵；A≥0表示A是一个Hermite正半定矩阵；AF是矩阵A的F-范数；v（A）表示矩阵A的非零特征值个数。

2 系统模型

考虑包括一个源节点（Source）,N个中继节点（Relays）、一个目的节点（Destination）和J 个窃听节点（Eavesdroppers）的无线网络模型，如图1所示。在此网络中，源节点距目的节点较远，因此认为不存在直接链路 S-D。假设源节点不知道窃听节点的确切位置，但知道其距离源节点较远，因此可以认为不存在直接链路 S-E。每个节点均安装单天线。假设所有节点处的噪声均是均值为 0、方差为2σ的复高斯白噪声。将多个单天线的勾结窃听者看作一个多天线的窃听者来处理。S-R, R-D, R-E的信道增益分别用f, c, G表示。

图1 系统模型

本文采用放大转发中继辅助的两阶段线性波束赋形方案。在第1阶段，源节点向中继节点发送信息；在第2阶段，中继对信号进行处理，并转发给目的节点，同时窃听节点也会接收到信号。在一个传输时隙内，源节点发送m个编码符号到中继节点。不失一般性地，我们用标量x表示在一个传输时隙内传输的符号。符号x具有单位功率，即 E { |x |2}= 1 。另外，为了符号的书写方便，省略时间下标。

在第1阶段，中继接收到的信号矢量为

式中，yR≜ [ yR,1yR,2… yR,N]T, yR,N表示在第N个中继节点处接收到的信号， PS是源节点的发送功率。

在第2阶段，N个中继节点对接收到的信号进行放大转发，并加入人工噪声，发送的信号为

在此阶段，中继转发消息信号和人工噪声所消耗的总功率为

目的节点和窃听节点接收到的信号分别为根据式（7），式（8）可以得出在目的接收端和窃听端所能达到的信息传输速率分别为

因此，系统可获得的最大保密速率[12]可以表示为

这里，保密速率是关于中继波束赋形加权矩阵W和人工噪声协方差矩阵Σ的函数。在源端发送功率和中继总功率固定的情况下，通过中继优化波束加权矩阵和人工噪声方差矩阵，可以使保密速率最大。

3 联合波束赋形和人工噪声的鲁棒性设计方案

3.1 设计方案的数学表述

假设已知R-E信道的CSI的不准确范围，利用零空间人工噪声和放大转发的中继波束赋形方法，基于半定规划理论，对中继的波束赋形加权矩阵和人工噪声协方差矩阵进行联合优化，以使在CSI误差最大的情况（称之为“最差情况”）下，减少可能勾结的多个窃听者获得的信息速率，使系统保密速率达到最大。这种最差情况下的优化方案称为零空间人工噪声辅助的保密速率最大化的鲁棒性设计（null-AN-aided Worst-Case Robust Secrecy Rate Maximization, null-AN-aided WCR-SRM）。假设

其中，G表示R-E链路的实际CSI,G表示获得的R-E链路的CSI估计值，ΔG表示信道的CSI误差，且该误差在一个范围内，可表示为[13]

其中，K=（1/ε）I是正定的J×J阶矩阵，ε＞0决定了窃听信道不准确范围的大小。式（15）可以等效为

因此，WCR-SRM设计问题可以表述为

3.2 优化问题的求解

由于 REws（W, Σ ） 的复杂度比较高，本文引入一个松弛变量β，以简化优化问题的目标函数。假设窃听端所获得的信息速率有一个上限（1/2）lgβ，则式（17）的 null-AN-aided WCR-SRM 优化问题可以写为

可以看出，由于变量G包含于一个集合Ω中，因此约束条件式（18a）对应于多个不等式。为了对优化问题进行简化，可以利用强化松弛的方法对式（18a）进行等效变换。

命题1 当W ≥ 0, Σ ≥0时，由式（18a）可以推导出式（19）

特殊地，当 v （ W ） = 1时，式（18a）与式（19）是等价的（证明可参考文献[5]）。

令X=ΔG，则G = G + X, GfH=GHdiag（f）= （ G + X ）Hdiag（f ），式（19）又可写为

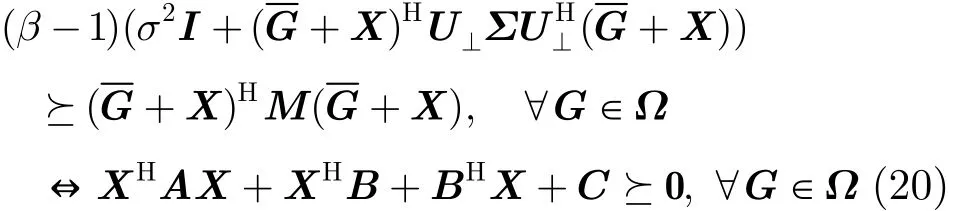
这里，A = （ β - 1 ）U⊥ΣU⊥H- M , B = [（β - 1）U⊥ΣU⊥H-M ]G,C= （ β - 1 ）（σ2I + GHU⊥ΣU⊥HG ） -GHMG ,M=PSdiag（f ）W d i ag（fH） - σ2（β - 1）dd（W ） 。

引理 1[14]令 f （ X ）= XHA X+XHB +BHX+C ,D≥0，则有式（21）成立。

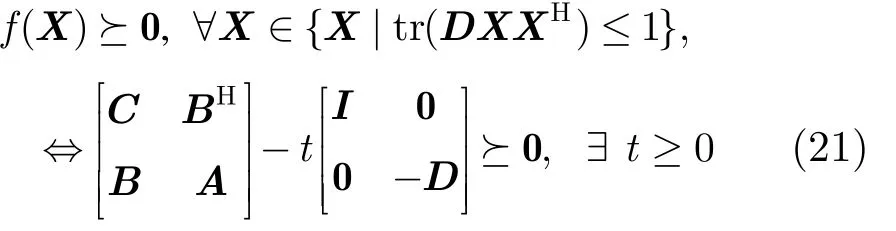
由于 ΔGF=XF≤ ε，即 t r（XXH） ≤ ε2。令D =（1/ε2）I，满足tr（DXXH）≤1。将引理1应用到式（20）可得

用式（22）代替约束条件式（18a）得到优化问题式（18）的一个紧松弛问题，可以表示为

其中，RS是问题式（23）的最优目标函数值。式（23）是式（18）的一个紧松弛问题，即RS= RS（证明过程参考文献[5]）。

另外，由于在实际的无线通信系统中保密速率RS≥ 0 ，则β 应满足

由于β 在范围 [1 , α0-1]内变化，α0=1/（1 + PSP||cf||2/σ4），式（23）的优化问题可以转换为1维变量优化问题，通过1维线性搜索方法来求解。

这里，α=1/β,lgγ=2RS, φ（ α）是优化问题式（23）在β给定的情况下的另外一种形式。式（26）的目标函数为拟凸函数，为了把式（26）转化为凸优化问题[15]，我们采用半定松弛方法[16]，并忽略隐含的约束条件 v （W ） = 1。同时根据 Charnes-Cooper 变换[17]，令 ξ = α （ σ2+ σ2t r（W Rcc））-1, Q=ξW, F=ξΣ, λ=ξt，从而式（26）的优化问题等价于

容易看出，式（27）中的目标函数为线性函数，且其约束条件均为线性矩阵不等式[18]，从而该问题是一个 SDP[15]问题，可利用已有的CVX工具箱[19]求解出全局最优解。由于变量α位于区间0[,1]α内，问题式（25）是一个关于单变量α的优化问题，可通过 1维线性搜索方法进行求解。这样，对于区间内任意一个固定的αi，都可以利用CVX工具箱解决式（27）的优化问题，从而计算出对应的 φ（ αi） 。然后可以得出最大的那个φ（ α），对应的α 值即为问题式（25）的最优解。由于不需求导的1维线性搜索方法一般仅限于优化函数单谷（峰）函数的情况，而本文中的优化函数为多峰函数，无法应用常用的1维搜索算法进行求解。因此在本文中外层采用全局搜索的方法求得其最优解。求解出问题式（25）的最优解后，对应地就可从式（27）的SDP问题中输出（Q*, F*, ξ*） ，从而得出 W*和Σ*。另外，由于使用了半定松弛方法，在问题转化过程中忽略了约束条件 v （W ） = 1。可通过拉格朗日法验证优化问题的 Karush-Kuhn-Tucker（KKT）条件[15]，证明最优解W*一定满足约束条件非零特征值个数等于 1，证明过程可参考文献[11]和文献[20]，限于篇幅，这里不再给出。

3.3 算法总结

由于本文方案的推导过程比较复杂，因此这里再对优化步骤总结如下：（1）根据信道系数f, c,G，计算出1维变量α的线性搜索区间[α0,1]；（2）外层采用全局搜索的方法。首先初始化搜索变量α0，并给出搜索步长δ。然后针对每一个 αi=αi-1+δ , αi≤ 1 ，内层利用CVX工具箱解决SDP问题式（28），可求解出对应的最大保密速率值 R （αi） = （1/2）⋅lg φ （ αi）。其中，δ为一小正数，决定优化结果的精度；（3）根据步骤（2）可得到不同α下的多个保密速率值 的 最 大 值 Rmax（ αo）= max{R （ α1）,R （ α2）,…,R （αi）,…} ，即是可获得的最大保密速率，相应的 1维变量最优值 αo对应的 W*和Σ*就是中继波束赋形加权矩阵和人工噪声协方差矩阵的最优解。

4 仿真结果及性能分析

在仿真中，假设信道是瑞利信道，增益服从均值为 0、方差为 1的独立复高斯分布，所有节点的噪声功率均为20 dBW σ= ，并且只考虑小尺度衰落。仿真中使用CVX[19]工具箱来解决SDP问题。

4.1 算法的搜索性能仿真

图2是算法的外层使用全局搜索的1维搜索方法，内层使用SDP方法时，不用搜索步长下可达到的最大保密速率的仿真曲线图。仿真中设置源端的发送功率为 PS= 1 0 dBW，中继发送总功率为 20 dBW 和 40 dBW，中继个数 N = 6 ，窃听者个数J= 2 。共进行了500次独立的蒙特卡洛仿真。从仿真结果曲线可以看出，当外层搜索次数越多，即搜索步长越小，得到的中继波束赋形加权矩阵和人工噪声协方差矩阵越准确，获得的保密速率越高。当外层搜索次数达到10次以上，即外层的全局搜索使用的搜索步长δ=0.1以下时，系统可获得的保密速率值就已经很接近最大值，而搜索次数在 16次以上，搜索次数再增加，保密速率的增加已不明显。本节的后续仿真中的搜索次数均设为20，即搜索步长为 δ = 0 .05。

4.2 不同方案下的保密速率性能仿真及分析

以下所有仿真均是进行 2000次独立的蒙特卡洛仿真，并对仿真结果取平均得到保密速率。

图3是不同窃听者个数、不同的窃听端CSI不准确性范围的情况下，中继消耗总功率与平均保密容量的关系曲线。仿真中固定设置源端的发送功率为PS= 1 0 dBW ，中继个数 N = 6 。从仿真结果可以看到，对于固定的中继总功率P，窃听者数量 J增加，使得窃听端所获得的保密速率增大，导致平均保密容量会减少。但是，随着中继总功率P的增加，不同窃听者个数下的平均保密容量的差距减少，这是因为P增加时，就有足够的功率用于发送人工噪声，从而减少信息的泄漏量。CSI不准确性范围ε越小，得到的平均保密容量越大。这是因为ε越小，表示设计W和Σ时所使用的信道 CSI估计值越接近真实值，最终得到的保密速率值越高。本文的方案具有很好的鲁棒性，CSI的误差对最终性能影响并不严重。如图所示，当 ε =0.01和ε=0.2时，后者的CSI不准确度是前者的20倍，而两种情况下应用本方案获得的保密速率值差距并不明显；同时，ε= 0 .01时本方案的性能与完美 CSI时的方案的性能基本一致，体现了本方案较好的抵抗不准确 CSI的能力。与没有人工噪声的 WCR（noAN-WCR）方案相比，随着中继消耗总功率P的增加，两种方案得出的保密速率曲线均是先增加，后趋于平行。这是因为当P较小时，较多的功率用于放大转发信号，没有多余的功率用来产生人工噪声，因此二者的性能基本一致。当P增大时，本文方案的保密速率继续上升，而WCR方案则增长缓慢。这是因为中继有更多的功率发送零空间人工噪声，能有效减少信息泄漏；当P增大到一定程度时，保密的速率增长趋于平缓，这是因为源端的发送功率固定，限制了信息的速率。

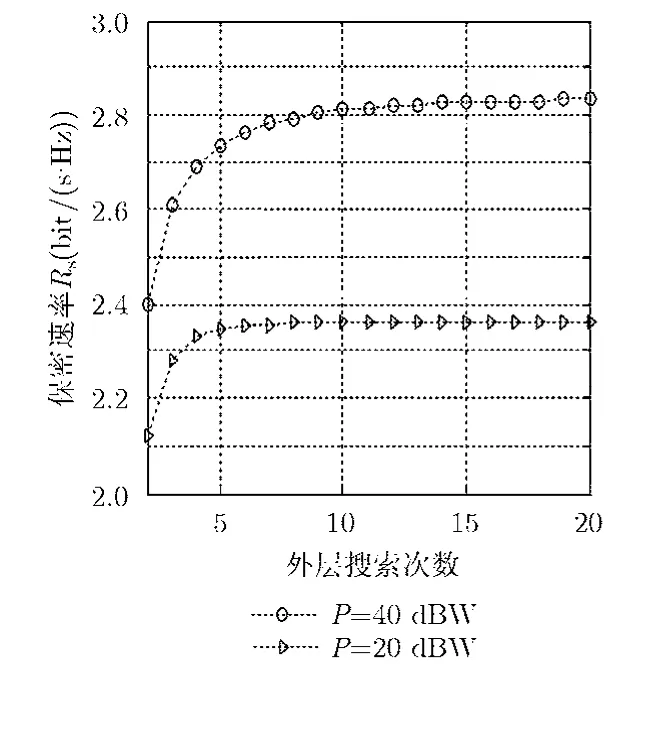
图2 搜索次数对保密速率的影响

图3 不同方案下中继消耗总功率对平均保密容量的影响

图4 null-AN-aided WCR-SRM方案 下中继个数与保密速率的关系

图4 中设置中继总功率 P = 4 0 dBW, CSI不准确性范围ε=0.2。在中继总功率足够大、CSI不准确性范围固定的情况下，给出不同中继数量、不同源节点发送功率、不同窃听者个数时保密速率的仿真结果。从仿真结果可知，随着源节点发送功率的增加，保密速率也会增大，因为源端发送的信息速率增加了。从横轴方向看，随着中继个数的增加，保密速率不断增大，这是因为增加中继节点相当于增加发送天线，相应可增加阵列增益，目的端接收到的信息量多于信息的泄漏量，并且两者的差距逐渐增大，使得总的保密速率相应增大。但是当中继个数增加到10个时，保密速率基本不再增加。这是因为中继数量达到一定程度时，阵列增益已经相当可观，再增加中继数量时，阵列增益的增加已不明显。从纵轴方向看，当中继个数 N = 2 时，中继处的发送天线数过少，基本上没有阵列增益，不能将人工噪声波束准确指向窃听者，而传输信息的信号的波束也不够窄，因此无论是窃听者数目 J = 2 或J= 6 ，窃听端都能获得较大的信息量，这样能获得的保密速率都很低， 6J= 时保密速率更低一点。当中继个数增加时，中继天线数增多，阵列增益逐渐增大，人工噪声波束能更准确地指向窃听者。但是窃听者越多，需要的干扰波束越多。而波束数量增加，则每个波束的指向性能会相应下降，对窃听者的干扰效果会有所下降。因此窃听者数量越多，其可窃取到的信息量就越大，故 6J= 时的保密速率要低于 2J= 时的保密速率。但当中继个数增加时，多干扰波束的性能持续改善，因此 2J= 和 6J= 的性能差距在逐渐减小。到 11N= 时，阵列增益已经相当可观，即使是在多个干扰波束的情况下，每个波束的效果也较好，因而在 2J= 和 6J= 时泄露的信息量差别已不大，相应能获得的保密速率值也趋近于相同。

5 结束语

本文对不存在直接链路的中继网络中的物理层安全传输技术进行研究。针对窃听端CSI不准确的情况，给出了一种中继波束赋形加人工噪声的传输方案，并采用全局搜索和半定规划方法对最差情况下的人工噪声的协方差和中继波束赋形矢量进行联合优化。同时也给出了相应的WCR-SRM保密速率的理论值。对于不同中继个数、不同窃听者个数、不同中继总功率、不同源节点发送功率以及不同的窃听信道CSI的不准确性范围等情况的保密速率进行了仿真和分析。仿真结果表明，采用本文的传输方案，即使在无法获得准确的窃听端CSI的情况下，系统的保密速率也能得到明显的改善。在实际运用中，可能会存在S-E间的直连链路，此情况下本文方案不再适用。在下一步的研究工作中，可针对S-E间存在直连链路的情况，对算法进行改进，对第 1阶段传输中窃听者的接收性能进行抑制，提高保密传输速率。

[1] Shannon C E. Communication theory of secrecy system[J].Bell System Technical Journal, 1949, 28（4）: 656-715.

[2] Leung-Yan-Cheong S K and Hellman M E. The Gaussian wiretap channel[J]. IEEE Transactions on Information Theory, 1978, 24（4）: 451-456.

[3] Yang Ye, Li Qiang, Ma W K, et al.. Cooperative secure beamforming for AF relay networks with multiple eavesdroppers[J]. IEEE Signal Processing Letters, 2013, 20（1）:35-38.

[4] Zhang Jun-wei and Gursoy M C. Collaborative relay beamforming for secrecy[C]. IEEE International Conference on Communications, Cape Town, 2010: 1-5.

[5] Li Qiang and Ma W K. Spatially selective artificial-noise aided transmit optimization for MISO multi-eves secrecy rate maximization[J]. IEEE Transactions on Signal Processing,2013, 61（10）: 2704-2717.

[6] Wang Hui-ming, Yin Qin-ye, and Xia Xiang-gen. Distributed beamforming for physical-layer security of two-way relay networks[J]. IEEE Transactions on Signal Processing, 2012,60（7）: 3532-3545.

[7] Goel S and Negi R. Secret communication in presence of colluding eavesdroppers[C]. IEEE Military Communications Conference, Atlantic City, NJ, 2005, Vol.3: 1501-1506.

[8] Pinto P C, Barros J, and Win M Z. Secure communication in stochastic wireless networks-part II: maximum rate and collusion[J]. IEEE Transactions on Information Forensics and Security, 2012, 7（1）: 139-147.

[9] Pinto P C, Barros J, and Win M Z. Wireless physical-layer security: the case of colluding eavesdroppers[C]. IEEE International Symposium on Information Theory, Seoul, 2009:2442-2446.

[10] Cai Chun-xiao, Cai Yue-ming, Yang Wei-wei, et al.. Secure connectivity using randomize-and-forward strategy in cooperative wireless networks[J]. IEEE Communications Letters, 2013, 17（7）: 1340-1343.

[11] Wang Chao and Wang Hui-ming. Robust joing beamforming and jamming for secure AF networks: low complexity design[OL]. http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=6847741, 2015.

[12] Liang Ying-bin, Gerhard K, Vincent H, et al.. Compound wiretap channels[J]. EURASIP Journal on Wireless Communications and Networking, 2009, 3（1）: 53-56.

[13] Li Quan-zhong, Zhang Qi, and Qin Jia-yin. Robust beamforming for cognitive multi-antenna relay networks with bounded channel uncertainties[J]. IEEE Transactions on Communications, 2014, 62（2）: 478-487.

[14] Luo Z Q, Sturm J F, and Zhang S. Multivariate nonnegative quadratic mappings[J]. Society for Industrial and Applied Mathematics Journal on Optimization, 2004, 14（4）:1140-1162.

[15] Boyd S and Vandenbeighe L. Convex Optimization[M]. UK:Cambridge University, 2004: 69-71, 168-169, 655.

[16] Luo Zhi-quan, Ma W K, So A M C, et al.. Semidefinite relaxation of quadratic optimization problems[J]. IEEE Signal Processing Magazine, 2010, 27（3）: 20-34.

[17] Charnes A and Cooper W W. Programming with linear fractional functionals[J]. Naval Research Logistics Quarterly,1962, 9（3）: 181-186.

[18] Boyd S, Ghaoui L E, Feron E, et al.. Linear Matrix Inequalities in System and Control Theory[M]. Philadelphia:Society of Industrial and Applied Mathematics, 1994: 7-9.

[19] Grant M and Boyd S. CVX: Matlab software for disciplined convex programming[OL]. http://cvxr.com/cvx/, 2013.

[20] Liao Wei-cheng, Chang T H, Ma W K, et al.. QoS-based transmit beamforming in the presence of eavesdroppers an artificial-noise-aided approach[J]. IEEE Transactions on Signal Processing, 2011, 59（3）: 1202-1216.