时空非均匀采样下双基地MIMO雷达收发角及多普勒频率联合估计方法

郑志东 方 飞 袁红刚 于彦明 陶 欢

1 引言

随着MIMO通信的快速发展、以及现代雷达研究的不断深入，多输入多输出（MIMO）雷达[13]-应运而生。其中，双基地MIMO雷达[412]-是将双基地雷达与MIMO技术相结合而形成的一种MIMO雷达体制，它不仅兼具了MIMO雷达在参数估计方面和双基地雷达在“四抗”方面的优势，还有效降低了双基地雷达在“三大”同步（空间、时间、频率）方面的要求，因而受到了广泛地关注。双基地MIMO雷达只需从接收信号中估计出目标的发射角（Direction Of Departure, DOD）和接收角（Direction Of Arrival, DOA），便可以实现对目标的定位，无需复杂的三大同步技术以及额外的收发通信链路支持，极大地简化了雷达的系统设备。

对未知目标的参数估计是雷达信号处理的一个关键内容，现有关于双基地MIMO雷达参数估计算法大都是针对静止目标或者假设目标多普勒频率已知，仅是对目标的发射角和接收角进行估计[48]-。目前，对于双基地MIMO雷达的收发角以及多普勒频率联合估计的研究很少，文献[9]给出了发射波束域-平行因子分析（PARAFAC）的目标角度和多普勒联合估计方法，通过对发射功率的充分聚焦，提高了接收端的信噪比，从而改善目标的参数估计性能；文献[10]利用相邻时刻接收的信号，提取出含有多普勒频率的旋转不变因子，再对接收数据进行重构，利用最小二乘算法估计出目标的DOD和DOA，并实现了自动配对；文献[11]利用收发阵列间的空间相位差以及多级延迟器之间的时间相位差，提取旋转不变因子，实现了目标的收发角度及多普勒频率联合估计，但该算法需要额外的配对算法，增加了计算量，而且文献[9-11]都只能用于收发阵列为均匀配置的情况，当收发阵列采用非均匀配置时，上述算法的性能将急剧下降；文献[12]将时域多级延迟器的输出作为第4维，提出了基于平行因子四线性分解的DOD, DOA以及多普勒频率联合估计算法，并实现了参数之间的自动配对，该方法本质上与平行因子三线性方法相一致。众所周知，双基地MIMO雷达具有阵列孔径扩展的优势，同时，采用合适的非均匀配置，也能扩展时域和空域的自由度，因此，如果能够将两者结合起来，将进一步扩展MIMO雷达的时域和空域自由度，从而获得更好的目标参数估计性能。

本文考虑发射、接收阵列以及多级延迟器皆为非均匀配置时的双基地 MIMO雷达联合参数估计问题。首先在接收端引入时域多级延迟器，建立双基地MIMO雷达时空信号模型，利用矩阵Khatri-Rao积的性质，对数据矩阵实施行置换运算，实现了MIMO雷达空域和时域虚拟二次自由度扩展，而后对所得数据进行时空“滑窗”处理，利用ESPRIT算法估计出目标的DOD, DOA和多普勒频率，并实现参数的自动配对。

2 时空信号模型

双基地 MIMO雷达的收发阵元采用非均匀配置，记 λ tm/2 （ m = 1 ,2,… , M ） 为M个发射阵元的位置， λ rn/2（n = 1 ,2,… , N ）为N个接收阵元的位置，分别以发射1号和接收1号阵元作为各自的参考阵元，即 t1= 0 ,r1= 0 。假设P个点目标位于收发阵列远场，第p个目标的DOD, DOA和多普勒频率分别为 θp, φp和 fdp。发射阵列发射不同的正交编码脉冲信号，在第 q（ q = 1 ,2,… , Q ）个发射脉冲下，接收端的匹配滤波输出为[11,12]

式 中 Ck=diag（ ej2πkτfd1T, ej2πkτfd2T, … ,ej2πkτfdPT） ∈CP×P,wk（q ） = w （ q + kτ）, k =0,1,…,K -1为延迟级数。将接收数据经过K级延时，并将所有的输出表示为列向量形式：

图1 K级非均匀延迟器

其中Y∈CMNK×P, D =[d （1）,d （2）,… ,d （Q）]∈ CP×Q为散射系数和多普勒信息构造的矢量，N为MNK×P维的噪声项。

3 基于二次自由度扩展的ESPRIT算法

由式（4），可求得接收数据的协方差矩阵为其中Λ=diag（h），由于各目标间互不相关，因此Λ为对角阵，且 h =[, …]T。

由式（4）可知，双基地 MIMO 雷达通过匹配滤波处理之后，本身具有空时孔径扩展的功能，即M发N收K级延迟的配置，将产生MNK个接收数据（一次自由度扩展）。以下通过对 RY的变换处理，使得在发射阵列、接收阵列、以及延迟器为最小冗余配置时，双基地MIMO雷达的空时孔径自由度进行再次扩展，得到大于 MNK维的虚拟接收数据，本文将其称为时空二次自由度扩展。

3.1 时空二次自由度扩展

进一步，对式（5）进行列向量化操作可得其中符号vec（.）和“*”分别表示向量化、共轭运算，1=[e1T,e2T, …]T∈R（MNK）2×1, ei∈RMNK×1表示第i（ i = 1 ,… , M NK）个元素为1，其他元素为0的列向量。在对式（6）进行数据变换之前，首先给出矩阵Khatri-Rao的计算规则。

122⊙D1，其中⊗表示Kronecker积，表示：仅矩阵的第（i, j）元素为1，其余元素项为0。同时矩阵的 Khatri-Rao积满足交换律 （D1⊙D2） ⊙ （F1⊙F2）=D1⊙ （ D2⊙ F1）⊙ F2。

利用上述性质 1，构造如下 （M N K ）2×（M N K）2的置换矩阵：

在式（8）的推导过程中，利用了矩阵Khatri-Rao的交换律性质。进一步，构造维数为（M N K）2×（ M N K）2的置换矩阵：

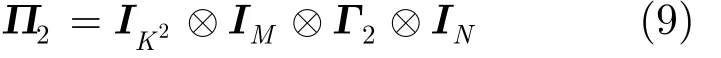
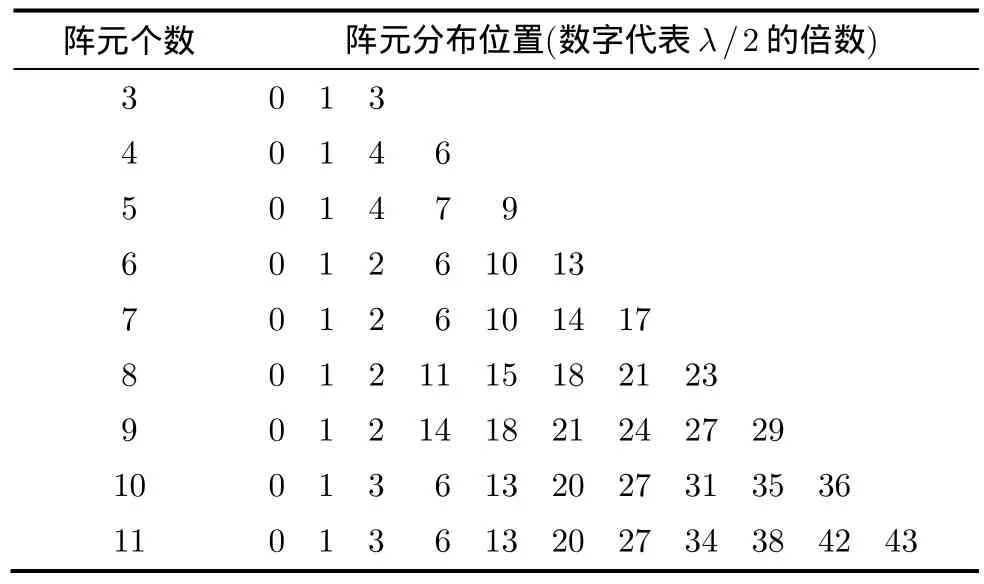
表1 最小冗余阵列

由式（11）可知，4元最小冗余阵的差分同置结构将获得位置为{-6:1:6}λ/2的虚拟阵元，并且只有在位置0处有4个冗余，其余位置均不存在冗余现象。由此便实现了由4个实体非均匀阵列，扩展成为13个虚拟孔径自由度的目的。

综上分析可知，为了得到最大的二次孔径扩展自由度，并获得最小的孔径冗余自由度，可以对发射阵列、接收阵列以及延迟器采用最小冗余配置方式（空域和时域均为非均匀采样）。这样既可以获得最大的二次孔径扩展自由度，也节约了收发阵列和延迟器配置的硬件成本。

与此同时，从式（11）进一步可知，尽管采用了最小冗余阵列配置，使得形成的扩展阵列具有最小的冗余度，但在个别阵元位置仍存在冗余。因此，首先应通过构造去冗余矩阵，对式（10）中的数据r进行去冗余处理。由于不同的最小冗余阵列配置下，经过差分同置结构的孔径扩展后，其冗余项的位置不同。因此，所需构造的去冗余矩阵也不相同，但对于某一固定的冗余阵列，可以预先离线设计好去冗余矩阵的结构。下面以式（11）中的结构为例，设计如下去冗余矩阵Γ：

将式（11）两边左乘去冗余矩阵Γ，可得新的方向矢量：

由式（13）可知，新的方向矢量中不再存有冗余项，它等效为13个均匀实阵元构成的方向矢量。上述仅以4个最小冗余阵为例来说明去冗余矩阵的构造，不失一般性，对于任意的最小冗余配置，都可以经过类似的方法实现去冗余处理。对式（10）左乘去冗余矩阵（空域和时域去冗余），则新的数据向量为

由式（14）可知，通过对协方差数据的一系列变换处理，实现了空域和时域孔径的二次自由度扩展，使得 MNK维数据扩展成（2M + 1 ）（2N + 1 ）（2K +1）维数据。这里将M发N收K级延迟所形成的MNK个接收数据称为一次自由度扩展（由 MIMO雷达的自身性质完成）。

3.2 数据矢量的时空“滑窗”处理

由于经过变维处理之后，数据r为列矢量，为此，本文基于文献[15]中多维频率估计的方法，对数据r进行空-时“滑窗”处理，将其转换为类似于协方差结构的数据矩阵。令M~= M +1, N~ = N +1,K~ = K + 1 ， 构 造 如 下M~N~K~ × （ 2M + 1 ）（2N +1）⋅（2K+1） 维的选择矩阵：

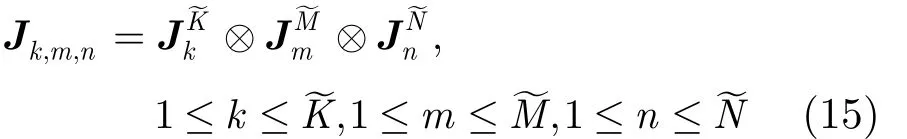
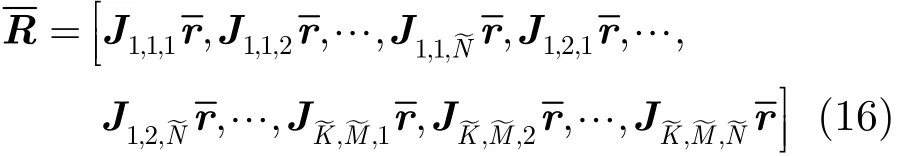
式（17）的化简过程可根据文献[15]中的附录 B推导~得到，在此不再详述。其中K= C（K~）⊙ B（M~）⊙A（N）为时空扩展导向矢量， （⋅ ）（i）表示取矩阵的后i行运算。

由式（17）可知，新得到的数据R具有与传统协方差相同的结构，因此，可以利用现有的多种算法[10-12]进行求解。为了方便计算，以下给出基于ESPRIT的求解方法。对R进行特征分解，可得由P个大特征值所对应的特征矢量构成的信号子空间Es∈，它与时空扩展导向矢量K张成相同的子空间，因此，存在可逆矩阵U使得 Es=KU-1。令 Es1和 Es2为 Es的前行，则根据导向矢量K的结构，有

其中 Φ （ fd） 为多普勒旋转不变因子。由式（18）可知，Us与U均为的特征矢量，两者之间满足：

其中Δ为列比例因子矩阵，H为列置换矩阵。由式（19）可知，Us和U之间仅是列的排列顺序和比例系数不同，并不会影响到 Us中行与行之间的比例关系。因此，可直接根据K︿= EsUs得到扩展导向矢量的估计值。当得到K︿之后，根据扩展导向矢量的内部结构，可进一步获得目标的发射角、接收角及多普勒频率的估计值。

由于收发角度以及多普勒频率均从同一列导向矢量中估计得到，因此所得三参量能够实现自动配对，虽然上述滑窗处理，对孔径自由度有一定的损失，但是由以下分析可以看出，本文算法的总孔径自由度仍然优于传统的算法。

对比式（5）和式（17）两个协方差矩阵可知，M发N收K级延迟的非均匀配置双基地MIMO雷达，利用本文算法可以将其等效为发收级延迟的均匀配置双基地 MIMO雷达，由于,M＞＞ N ,＞ K ，因此，本文算法极大地扩展了空域和时域的孔径自由度。例如：对于4发4收4级延迟的非均匀配置MIMO雷达（64维孔径自由度），最终可扩展为7发7收7级延迟的均匀配置MIMO雷达（7×7×7=343维孔径自由度）。与此同时，为了保证参数唯一可识别性，信号子空间 Es1和 Es2都应满足列满秩，即P ≤ K （ M + 1 ）（N + 1 ） ，因此，本文算法的最大可识别目标数目为K（ M + 1 ）（N + 1 ），而对于发射、接收、延迟器采用均匀配置的双基地MIMO雷达，其最大可识别目标数为MN（ K- 1 ），因此，本文算法极大地提高了目标的最大可识别数目。

4 实验仿真和数据分析

本节首先验证所提算法的有效性，并与文献[11]中的多维 ESPRIT算法、文献[12]中的四线性分解算法（QALS）的参数估计性能进行比较。假设目标处于复高斯白噪声背景下，其散射系数服从复高斯分布，发射端发射相互正交的Hadamard编码信号，且在每个重复周期内的相位编码个数 256，分别进行如下实验。

实验 1 算法的有效性验证 考虑 4发 4收 4级延迟的双基地MIMO雷达配置情况，利用本文算法进行参数估计时，发射阵列、接收阵列以及多级延迟器均采用最小冗余配置方式，即 { tm}m4

=1=0.5λ [ 0 , 1,4,6], { rn= 0 .5λ [0 , 1,4,6]，延迟器组的各级延时为[0 , 1,4,6] τ。利用多维ESPRIT算法时，收发阵列采用半波长均匀配置，延迟器采用等均匀延时。假设存有 3个不相关目标，其位置为：（60°,1 5°,1 0 0 Hz）,（10°,- 4 0°,2 0 00 Hz）,（- 4 0°,- 5°,1300 Hz），脉冲数 Q = 1 00，重复周期为 T = 1 0-4s。

图 2（a）和 图 2（b）分 别 为 本 文 算 法 与 多 维ESPRIT算法下目标的定位结果。实验时 Monte-Carlo次数为200, SNR=0 dB。由图2可知，本文算法能够实现对多目标的发射角、接收角和多普勒频率的联合估计，且实现了参数间的自动配对。比较图 2（a）和图 2（b）可知，在 SNR=0 dB 时，本文算法的估计精度优于多维ESPRIT算法。

实验 2 不同算法间的估计性能比较 比较本文算法、QALS算法以及多维ESPRIT算法的估计性能。目标的个数以及位置参数同实验 1。当利用本文算法进行求解时，仿真条件与实验1相同（空域和时域均采用最小冗余配置 M=N=K=4），当利用QALS算法和多维ESPRIT算法时，发射、接收阵列以及多级延迟器采用均匀配置，且参数设置为M=N=K=5。图 3（a）, 3（b）和 3（c）分别为 3 种不同算法下目标参数估计的RMSE随SNR的变化曲线。

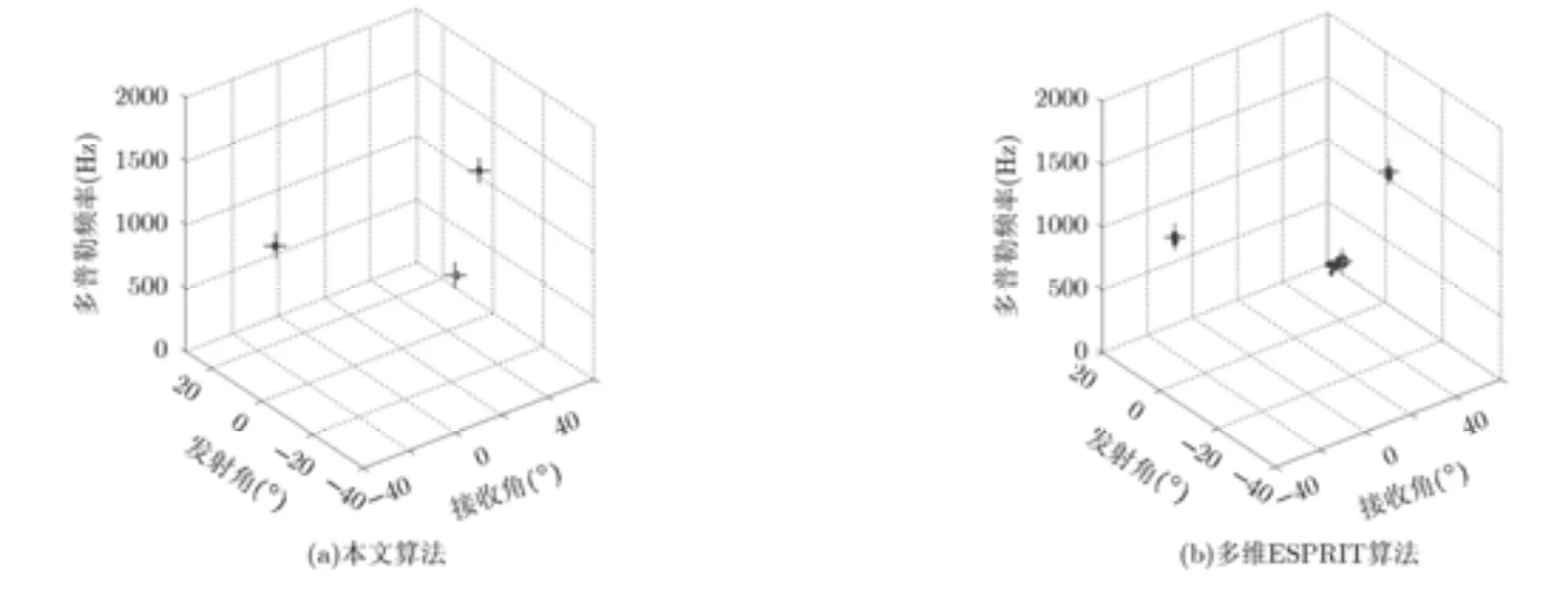
图2 两种算法的目标定位结果

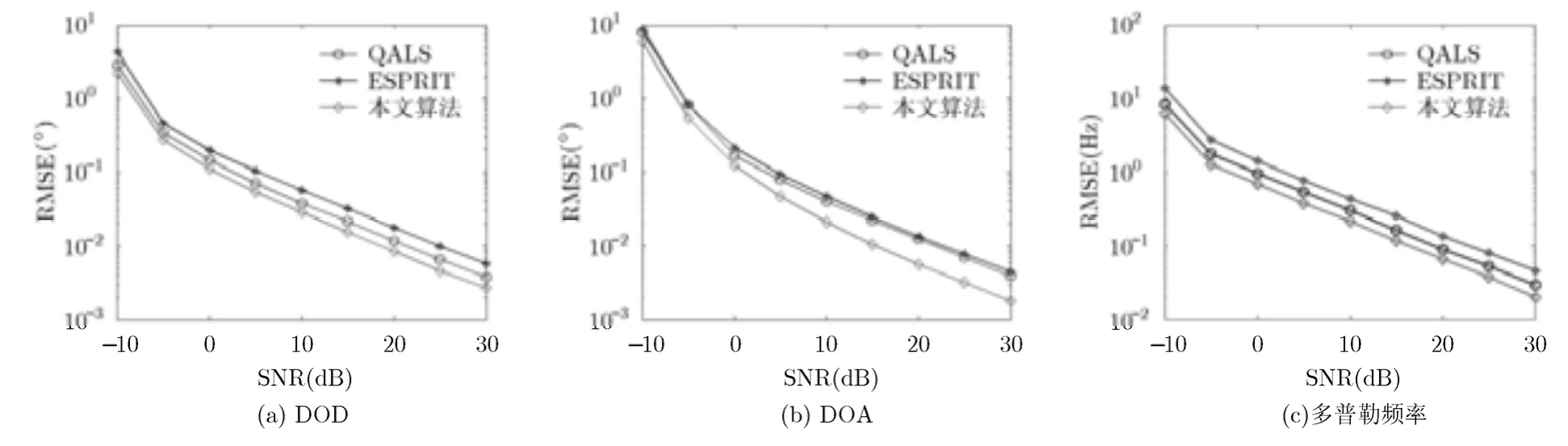
图3 目标DOD, DOA及多普勒频率的RMSE随SNR变化曲线

由图3可知，不论在高SNR还是低SNR条件下，本文算法的参数估计精度最优，QALS算法性能次之，而多维ESPRIT的3个参数估计性能均差于上述两种算法。这主要是由于：虽然在设置仿真条件时，本文算法所用到的实体阵元数和延迟级数少于QALS算法和多维ESPRIT算法，但由于空域和时域孔径的二次虚拟扩展，使得虚拟扩展后的总孔径维数为M~ × N~ × K~ =7 × 7×7 =343，而QALS算法和多维 ESPRIT算法扩展的虚拟孔径数为M×N×K=5 × 5 × 5 =255，因此，经过二次虚拟孔径扩展，使得本文算法所能利用的孔径自由度大于QALS算法和多维ESPRIT算法，因此，本文算法均有最高的估计精度。与此同时，由于多维ESPRIT算法存在一定的阵元孔径损失，而QALS算法利用了全部的输出信息，且经过每次迭代都有精确的最小二乘闭式解，因此QALS算法的估计性能优于多维ESPRIT算法。

5 结论

针对发射、接收阵列和多级延迟器皆为非均匀配置的MIMO雷达，本文提出了基于空域和时域二次自由度扩展的 ESPRIT新算法。首先利用矩阵Khatri-Rao积的性质，对接收数据进行行置换和去冗余运算，实现了最小冗余配置下空域和时域孔径自由度的二次扩展，然后将数据进行矩阵换维操作，利用ESPRIT算法分别估计出目标的收发角及多普勒频率，并实现了各参数的自动配对。理论和仿真实验表明：通过时空虚拟孔径的二次自由度扩展，能够将非均匀配置阵列等效为收发阵元数及延迟级数均大于实体数目下的均匀配置形式，极大地扩展了空域和时域的孔径自由度。在同等实体阵元和延迟级数情况下，本文算法的估计精度优于四线性分解算法和多维ESPRIT算法，较传统双基地MIMO雷达，本文算法能够识别出更多的目标。此外，通过最小冗余配置，减少了阵列中的冗余信息，极大地降低了阵列和延迟器的配置需求，更利于实际工程应用。

[1] Dionysios S K and Athina P P. Matrix completion in collocated MIMO radar: recoverability, bounds & theoretical guarantees[J]. IEEE Transactions on Signal Processing, 2014,62（2）: 309-321.

[2] 唐波, 张玉, 李科, 等. 杂波中MIMO雷达恒模波形及接收机联合优化算法研究[J]. 电子学报, 2014, 42（9）: 1705-1711.Tang Bo, Zhang Yu, Li Ke, et al.. Joint constant-envelope waveform and receiver design for MIMO radar in the presence of clutter [J]. Acta Electronica Sinica, 2014, 42（9）: 1705-1711.[3] Haimovich A M, Blum R S, Lenard J, et al.. MIMO radar with widely separated antennas[J]. IEEE Signal Processing Magazine, 2008, 25（1）: 116-129.

[4] Chen Duo-fang, Chen Bai-xiao, and Qin Guo-dong. Angle estimation using ESPRIT in MIMO radar[J]. Electronics Letters, 2008, 44（12）: 770-771.

[5] 孙中伟, 张小飞, 吴海浪, 等. L型阵列双基地MIMO雷达的传播算子多维角度估计[J]. 应用科学学报, 2014, 32（4）: 57-64.Sun Zhong-wei, Zhang Xiao-fei, Wu Hai-lang, et al..Multi-dimensional angle estimation in bistatic MIMO radar for L-shaped array with propagator method[J]. Journal of Applied Sciences, 2014, 32（4）: 57-64.

[6] Chen Chen, Zhang Xiao-fei, and Ben De. Coherent angle estimation in bistatic multi-input multi-output radar using parallel profile with linear dependencies decomposition[J].IET Radar, Sonar & Navigation, 2013, 7（8）: 867-874.

[7] 孙理, 朱晓华, 贺亚鹏, 等. 双基地稀疏阵列MIMO雷达快速多目标定位方法[J]. 电子与信息学报, 2013, 35（5）: 1142-1148.Sun Li, Zhu Xiao-hua, He Ya-peng, et al.. Fast multi-target localization with sparse array in bistatic MIMO radar[J].Journal of Electronics & Information Technology, 2013, 35（5）:1142-1148.

[8] 李小波, 梁浩, 崔琛. 基于四元数和增广矩阵束的 MIMO 雷达角度估计算法[J]. 数据采集与处理, 2014, 29（4）: 579-583.Li Xiao-bo, Liang Hao, and Cui Chen. Angle estimation in bistatic MIMO radar based on quaternion and MEMP[J].Journal of Data Acquisition and Processing, 2014, 29（4）:579-583.

[9] 郑志东, 张剑云, 杨瑛. 基于发射波束域-平行因子分析的MIMO雷达收发角度估计[J]. 电子与信息学报, 2011, 33（12）:2875-2880.Zheng Zhi-dong, Zhang Jian-yun, and Yang Ying. Joint DOD-DOA estimation of MIMO radar based on transmit beamspace-PARAFAC[J]. Journal of Electronics &Information Technology, 2011, 33（12）: 2875-2880.

[10] Cao Y H. Joint estimation of angle and Doppler frequency for bistatic MIMO radar[J]. Electronics Letters, 2010, 46（2）:170-172.

[11] 刘帅, 张弓, 刘文波. 基于时空结构的双基地 MIMO 雷达多维参数联合估计[J]. 航空学报, 2010, 31（6）: 1196-1203.Liu Shuai, Zhang Gong, and Liu Wen-bo. Multi-dimensional parameter joint estimation of bistatic MIMO radars based on temporal-spatial structure[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31（6）: 1196-1203.

[12] 李建峰, 张小飞. 基于四线性分解的双基地 MIMO 雷达的角度和多普勒频率联合估计[J]. 航空学报, 2012, 33（8）:1474-1482.Li Jian-feng and Zhang Xiao-fei. Joint estimation of angle and Doppler frequency in bistatic MIMO radar based on quadrilinear decomposition[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33（8）: 1474-1482.

[13] Pal P and Vaidynanthan P P. Nested arrays: a novel approach to array processing with enhanced degrees of freedom[J]. IEEE Transactions on Signal Processing, 2010,58（8）: 4176-4181.

[14] Moffer A T. Minimum-redundancy linear arrays[J]. IEEE Transactions on Antennas and Propagation, 1968, 16（2）:172-175.

[15] Liu J and Liu X Q. An eigenvector-based approach for multidimensional frequency estimation with improved identifiability[J]. IEEE Transactions on Signal Processing,2013, 54（12）: 4543-4556.