基于时间-调频斜率分布的多普勒调频率估计

汪金真 宿绍莹 陈曾平

1 引言

在ISAR成像中，尤其在高分辨成像中，正确估计出目标回波线性调频（Linear Frequency Modulated, LFM）信号的多普勒调频斜率后对成像结果进行补偿，可以有效提高成像质量。最大似然法[1]基于2维搜索具有最优的性能，但是运算量大。为了克服这个问题。文献[2]提出基于相位域的调频斜率估计算法，简化了运算。文献[3]采用相位线性拟合的方法大大提高了计算效率。文献[4]提出了短时傅里叶变换调频直线线性拟合的方法，较精确地估计出LFM信号的调频斜率；但是它们都只能用于单分量LFM信号的场合。在多分量LFM信号应用场合，Wigner-Ville分布[5]对各分量LFM信号具有最佳的时频聚集性，但存在交叉项的影响，通过Hough变换[6,7]可以一定程度上抑制交叉项。分数阶傅里叶变换（Fractional Fourier Transform, FrFT）[8]和离散chirp傅里叶变换[9]都是比较有效的方法，但它们都需要 2维搜索。离散多项式变换[10,11]计算量小，但要求较高的信噪比。文献[12,13]提出时间-调频斜率分布（Time Chirp Distribution, TCD）的定义并作了改进，文献[14,15]将TCD应用在多分量线性调频信号的检测与参数估计当中并提出了多分量线性调频信号交叉项的抑制方法。文献[16]改进了三次相位函数计算方法，较快实现了多分量LFM信号参数估计，但它们都是直接针对线性调频信号进行研究的，对目标回波线性调频信号则研究甚少。

本文建立了单散射点和多散射点目标回波模型并分析其瞬时相位特点，提出了基于 TCD的多普勒调频斜率估计算法。针对多散射点目标回波的TCD的自项和交叉项均在多普勒调频斜率处取得极值的特点，采用垂直调频斜率轴投影积分有效抑制非多普勒调频斜率交叉项和噪声，增强多普勒调频斜率项，通过二次搜索投影积分的最大值位置估计多普勒调频斜率，减少了计算耗时。仿真表明，该方法具有很好的单散射点和多散射点目标回波多普勒调频斜率估计性能。

2 目标回波模型

在高斯白噪声环境下目标回波模型可表示为

式中，t是时间；P是散射点数； { sm（t） }1是与目标 P个散射点相对应的回波线性调频信号；w（t）是与信号无关的均值为0、方差为 δ2的高斯白噪声。

距离雷达为Rm的散射点回波LFM信号经距离压缩后的信号为

式中，A为幅度；fi为起始频率；Tp为脉宽；k为调频率；c为电磁波传播速度；散射系数为σm; λ为波长。对于单散射点回波，记瞬时相位为 θm（t），

从式（3）可以看出，瞬时相位 θm（t）是时间t的二次函数，对 θm（t）进行多项式拟合可以估计出多普勒调频斜率k。对于多散射点目标回波 ∑ sm（t ），虽然各分量相位的二次项系数均为 k的π倍，但回波相位是各分量的合成相位，不等于各分量相位的线性叠加，因此，必须采用新方法估计多普勒调频斜率k。

3 时间-调频斜率（TCD）分布

3.1 TCD分布及自项分析

类似WVD定义，信号x（t）的TCD分布定义[12]为

考虑距离雷达 R、散射系数为σ的单散射点的回波 LFM 信号 x（t），将 x（t）代入式（4），可得

从式（5）可以看出，对于任意时刻t，当u=k, T C （ t, u）均具有极大值，并且以极值点为中心沿着调频斜率轴急剧下降，而加性高斯白噪声不具有这种特性。

图 1（a）是单散射点目标模型，图 1（b）是该单散射点目标回波LFM信号的TCD，采样点数2501，采样频率为 10 MHz，调频斜率为 - 1.6 × 10-4MHz/μs，信噪比为1 dB。从图1（b）可以看出，单散射点回波LFM信号的TCD在时间-调频斜率平面投影为一条垂直于调频斜率轴的直线，任意时刻的极大值位置均落在该直线上。

3.2 交叉项分析

考虑多散射点目标上任意两个散射点的回波LFM 信号 sm1（t）, sm2（t）, sm1（t）与 sm2（t）之间的 TCD的交叉项为

将式（2）代入式（6），计算可得

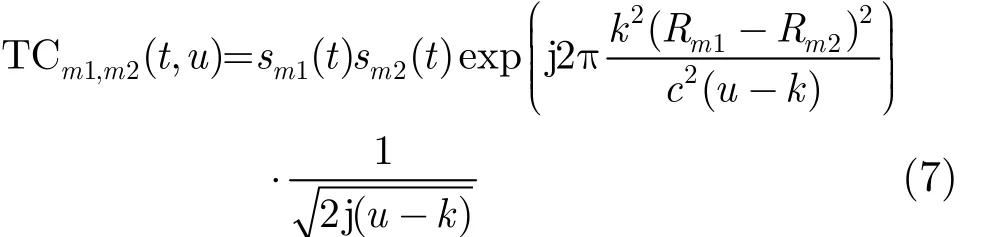
图1 单散射点目标模型及回波LFM信号的TCD

由式（7）可以看出，任意时刻 t，当 u=k 时，sm1（t）与sm2（t）之间的TCD的交叉项绝对值TCm1,m2（t, u）将取得极大值。式（7）取绝对值可得

记多散射点目标回波LFM信号的TCD交叉项为 T Ccross（t, u），有

将式（7）代入式（9）中，可得

由式（10）可知，在任意时刻 t，多散射点目标回波LFM信号的 TCD交叉项TCcross（t, u）也将在u=k处取得极大值。

3.3 多散射点目标回波LFM信号的TCD

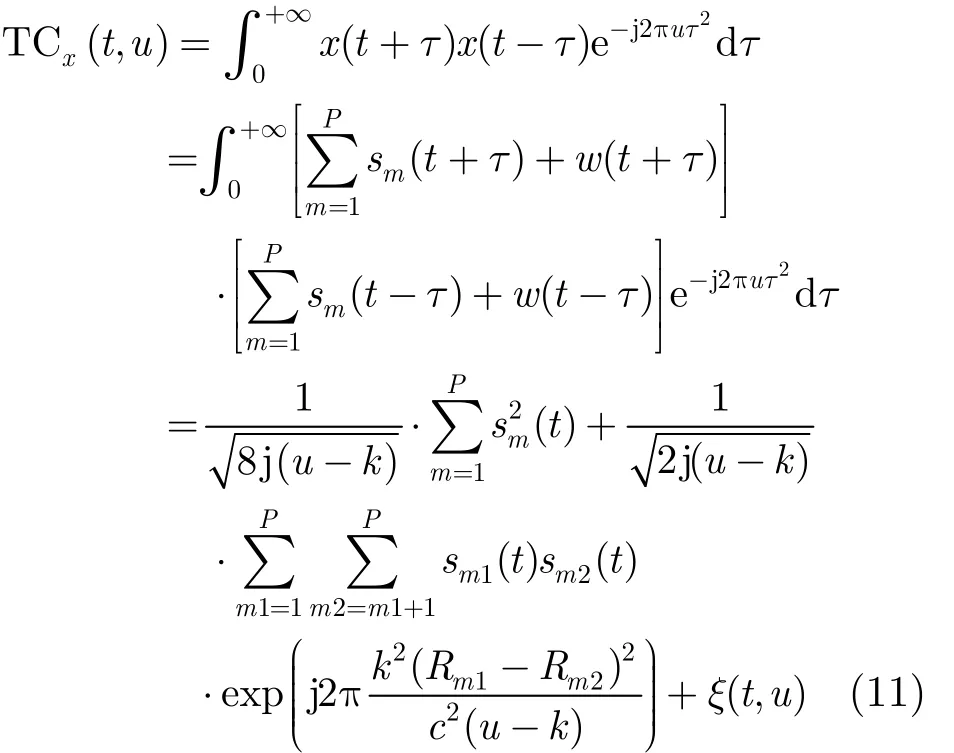
综合3.1节和3.2节的分析，可以得到多散射点目标回波 LFM 信号 x（t）的 TCD，记为 TCx（t,u） ，如式（11）所示。式中，噪声w（t）的TCD 自项以及噪声 w（t）与各散射点回波 LFM 信号sm（t）的交叉项一起记为（,）t uξ。从式（11）可以看出，对于无噪的多散射点目标回波LFM信号，其TCD分布将没有与噪声有关的最后一项，任意时刻t, T Cx（t, u）将在u = k 处取得峰值；对于含噪情况，噪声项 ξ（t, u）出现，会使得x（t）的TCD噪底增强，峰值相对不再尖锐，此外，还有可能出现一些虚假伪峰。

图 2（a）是多散射点飞机目标模型，图 2（b）是该多散射点目标回波的TCD，采样频率为10 MHz，采样点数 2501，调频斜率为 - 1 .6× 1 0-4MHz/μs，信噪比为5 dB。从图2（b）可以看出，在多散射点目标模型下，交叉项TCcross（t, u）在LFM信号调频斜率值处取得极大值，该极大值位置与自项极大值位置大致重叠在一起，TCD在时间-调频斜率平面投影仍然为一条近似垂直于调频斜率轴的直线，受噪声和交叉项的影响，该直线不是很紧凑，极值点不是严格地分布在该直线上，而是分布在该直线具有一定邻域的条带内，该直线上各点的分布强度显然不如图 1（b）中单散射点情况的分布强度均匀，但从统计学上，该直线条带的中心线为 k =-1.6 × 10-4MHz/μs，任意时刻的极值点对应的调频斜率都将趋近 1 .6×10-4MHz/μs。

4 多普勒调频斜率估计

4.1 参数估计

记 x（t）的 TCD 分布为离散形式为 TCx（n,u），定义垂直调频斜率轴投影积分累积量（）uΛ

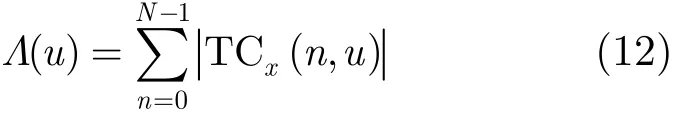
由于多散射点目标回波LFM信号的TCD的交叉项和自项均在u=K处取得极值，且以极值点为中心沿着调频斜率轴急剧下降，通过式（12）可以很好累积多普勒调频斜率处的自项和交叉项，即增强多普勒调频斜率项，同时抑制非多普勒调频斜率处的交叉项和噪声。 Λ（u）相当于TCx（n, u ） 对整个时间轴进行积分，可看作 T Cx（n, u ） 在零度角上的离散Radon变换[17]，由于只在一个角度上进行Radon变换，因而运算量小。

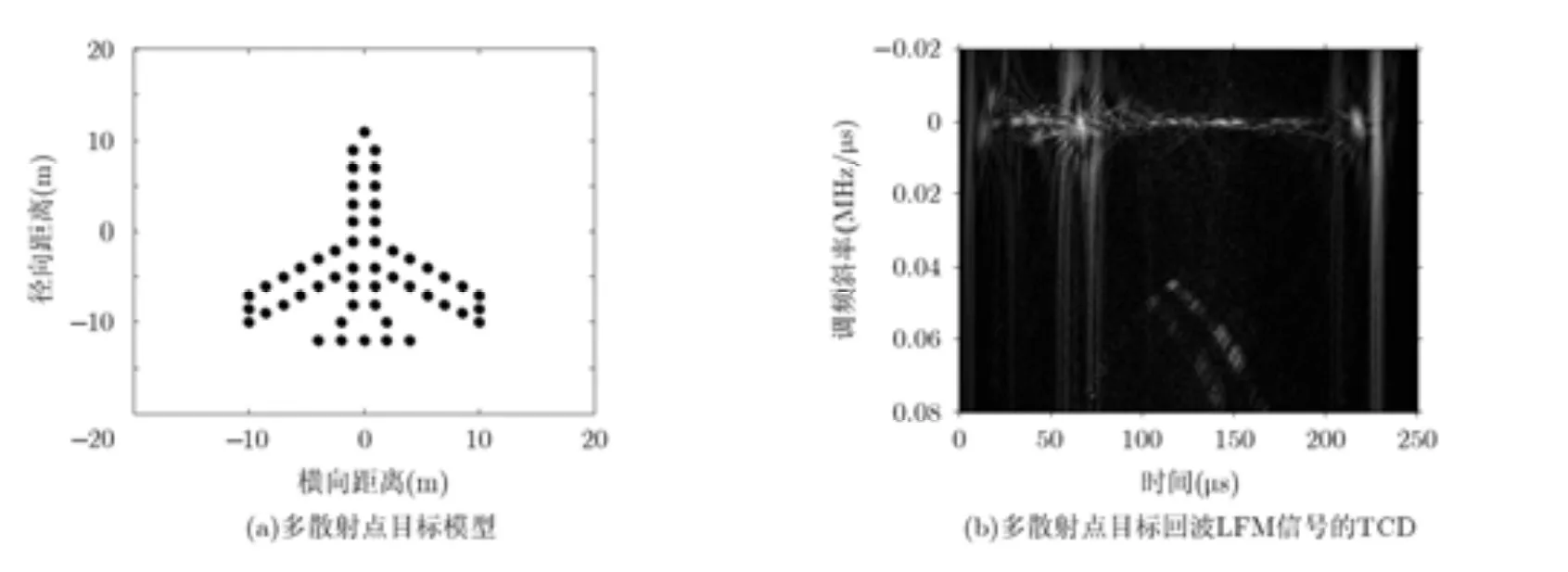
图2 多散射点目标模型及回波LFM信号的TCD

图3 给出了单散射点和多散射点目标回波TCD在垂直调频斜率轴上进行投影积分的情况，单散射点和多散射点目标回波TCD分别如图1（b），图2（b）所示。从图3中可以看出，经过垂直调频斜率轴投影积分累积后，多普勒调频斜率项得到了有效增强，非多普勒调频斜率项得到了有效抑制，因此，可通过搜索（）uΛ最大值位置估计出多普勒调频斜率。为了较少计算耗时，本文采用一次粗搜索方法获取积分累积量（）uΛ最大值粗略位置基础上进行二次精搜索的方法来精确估计多普勒调频斜率，具体方法为：

（1）根据式（11）计算 x（t）的 TCD 分布 TCx（t, u），其离散形式记为 TCx（n,u）；

（2）根据式（12）计算 TCx（n,u）的垂直调频斜率轴投影积分，得到（）uΛ；

（3）设置 u的初级搜索步长 Nstep1，在u的离散取值范围 - 1 / N + Nstep1, 1/N - Nstep1内搜索 Λ（u）的最大值以及相邻的次最大值、次次最大值的位置M1, M2, M3；

（4）取M2, M3中较小值赋给 Mmin，较大值赋给Mmax，设置 u的精细步长 Nstep2, u =Mmin, Mmin+Nstep2, Mmin+ 2 Nstep2, … ,Mmax，重新计算 TCx（n,u），重复步骤（2），在u的离散取值范围[Mmin, Mmax]内搜索Λ（u）的最大值的精细位置M︿；

（5）根据数字多普勒调频斜率公式 K = k Ts2，得到多散射点目标回波 LFM 信号多普勒调频斜率精估计值ˆk 为

4.2 计算量分析

表1，表2分别分析了N为奇数和偶数情况下计算TCD的所需的复数乘法和复数加法量，Λ（u）计算所需的复数加法量以及 Λ （ u ）最大值搜索总次数，最大值搜索次数包括第1次搜索次数和第2次搜索次数，均与Nstep1, Nstep2有关。

表1 TCD计算量分析（N为奇数）

表2 DCD计算量分析（N为偶数）

其中复数乘法最耗时，记复数乘法次数为N*，在N一定的情况下，N为奇数时，

图3 单散射点和多散射点目标回波TCD在垂直调频斜率轴上的投影积分

N为偶数时，

当 且 仅 当 1 /（N Nstep1） = （ Mmax- Mmin） /Nstep2， 即Nstep2=NNstep1（ Mmax- Mmin） 时，式（21）和式（22）取得最小值，此时 N*min= 2 （N + 1 ）（N - 1）/（N Nstep1）或 N*min= 2 （N + 2 ）/Nstep1。取 Nstep1=1/（100N ） ，则Nstep2= （ Mmax- Mmin）/100, N*min= 2 00（N + 1）⋅（N-1）或N*min= 2 00（N + 2 ）N。

5 实验结果与分析

为了验证本文算法的有效性，对不同模型的数据进行仿真实验。单散射点目标模型和多散射点目标模型分别如图 1（a），图 2（a）所示，回波 LFM 信号采样点数 N=2501，采样频率 fs=10 MHz，调频斜率均为 k =-1 .6× 1 0-4MHz/μs 。

图4给出了单散射点情况下的多普勒调频斜率估计性能曲线，并与二次相位拟合法（Quadratic Phase Fitting, QPF）、平滑二次相位拟合法（Smoothed Quadratic Phase Fitting, SQPF）, FrFT法进行了比较。实验中TCD法中 Nstep1=1/（100N ）,Nstep2= （ Mmax- Mmin）/100，平滑二次相位拟合法的平滑窗选用点数为11的中值滤波器。从图中可以看出，QPF在较高的信噪比下具有较好的性能，当SNR≥11 dB时，QPF的性能优于FrFT；但当SNR减小时，二次相位关系变差，QPF的性能急剧恶化，明显次于FrFT。SQPF在一定信噪比范围内能够改善二次相位关系，SNR≥9 dB时，SQPF的性能优于FrFT，当SNR降低时，对相位的平滑也无济于改善二次相位关系，SQPF失效。FrFT具有较稳定的性能，RMSE与SNR近似成线性 dB关系。当SNR ≥ -8 dB 时，本文 TCD法的性能明显优于QPF, SQPF, FrFT，而且当SNR ≥ -5 dB ，均方根误差保持在一个很低的稳定水平。

图4 单散射点目标回波LFM信号多普勒调频斜率估计性能

图5 给出了多散射点情况下的多普勒调频斜率估计性能曲线，并与 FrFT法进行了比较。从图中可以看出，SNR在-7～0 dB范围内时，本文TCD法的性能优于FrFT法的性能；当SNR≥1 dB时，本文TCD法的性能趋于稳定。在-7～15 dB范围内，本文算法较 FrFT法具有更好的抗噪性能，这主要是因为多散射点目标回波LFM信号的TCD分布在调频斜率处进行时间上的累积可以有效抑制噪声和非多普勒调频斜率处的交叉项，而多散射点目标回波LFM信号的FrFT峰值受噪声影响很大。

6 结束语

本文针对单散射点和多散射点目标回波相位自身的特点，提出了基于 TCD的多普勒调频斜率估计算法，采用垂直调频斜率轴投影积分可以有效抑制 TCD的非多普勒调频斜率交叉项及噪声、增强多普勒调频斜率项，计算量分析表明，通过改变数字调频斜率的步长，可以调节总计算量，使得复数乘法次数在一定条件下达到最小。仿真实验验证了该算法的有效性，单散射点情况下，SNR 3 dB≥-时，该算法的性能优于FrFT, QPF, SQPF；多散射点情况下，该算法的整体抗噪性能优于FrFT。虽然TCD计算量较大，然而，随着计算机的发展，其处理能力提升，该问题非常容易得到解决，因此，本文算法具有较好的工程指导意义。

图5 多散射点目标回波LFM信号多普勒调频斜率估计性能

[1] Tao R, Feng Y, and Wang Y. Theoretical and experimental study of a signal feature extraction algorithm for measuring propeller acceleration in a port surveillance system[J]. IET Radar, Sonar & Navigation, 2011, 5（2）: 172-181.

[2] 金胜, 王峰, 邓振淼, 等. 一种 LFM 信号相位域快速高精度参数估计算法[J]. 系统工程与电子技术, 2011, 33（2）: 264-267.Jin Sheng, Wang Feng, Deng Zhen-miao, et al.. Fast and accurate estimator on parameters of chirp signals in phase domain[J]. Systems Engineering and Electronics, 2011, 33（2）:264-267.

[3] 牛萌, 李钊, 朱晓光, 等. LFM信号参数估计的最大似然改进算法[J]. 无线电通信技术, 2009, 35（3）: 59-61.Niu Meng, Li Zhao, Zhu Xiao-guang, et al.. Improved maximum likelihood estimation algorithm to estimate parameters of LFM signal[J]. Radio Communications Technology, 2009, 35（3）: 59-61.

[4] Wang J Z, Su S Y, and Chen Z P. Parameter estimation of chirp signal under low SNR[J]. Science China Information Sciences, 2015, 58: 020307（13）.

[5] Chen G H, Ma S W, Qin T H, et al.. Geometryinformation-aided efficient motion parameter estimation for moving-target imaging and location[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12（1）: 155-159.

[6] Zeng D, Zeng X, and Tang B. Automatic modulation classification of radar signals using the Rihaczek distribution and Hough transform[J]. IET Radar, Sonar & Navigation,2012, 6（5）: 322-331.

[7] Jia S Y, Wang G H, and Tan S C. Radial acceleration estimation of multiple high maneuvering targets[J]. Journal of Systems Engineering and Electronics, 2014, 25（2）: 183-193.[8] Miah K and Potter D. Geophysical signal parameterization and filtering using the fractional Fourier transform[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7（3）: 845-852.

[9] Wu L, Wei X Z, Yang D G, et al.. ISAR Imaging of targets with complex motion based on discrete chirp Fourier transform for cubic chirps[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50（10）: 4201-4212.

[10] 高春霞, 张天骐, 金翔, 等. 基于离散多项式变换的宽带线性调频信号波达方向估计[J]. 计算机应用, 2011, 31（10）:2872-2875.Gao Chun-xia, Zhang Tian-qi, Jin Xiang, et al.. Arrival direction estimation of wideband linear frequency modulation signal based on DPT[J]. Journal of Computer Application,2011, 31（10）: 2872-2875.

[11] 庞存锁. 基于离散多项式相位变换和分数阶傅里叶变换的加速目标检测算法[J]. 电子学报, 2012, 40（1）: 184-188.Pang Cun-suo. An accelerating target detection algorithm based on DPT and fractional Fourier transform[J]. Acta Electronica Sinica, 2012, 40（1）: 184-188.

[12] Peter O. A fast algorithm for estimating the parameters of a quadratic FM signal[J]. IEEE Transactions on Signal Processing, 2004, 52（2）: 385-393.

[13] Maree F and Peter O. Extending the performance of the cubic phase function algorithm[J]. IEEE Transactions on Signal Processing, 2007, 55（10）: 4767-4774.

[14] 杜雨洺, 杨建宇. 基于时间-调频斜率分布的多线性调频信号检测与参数估计[J]. 电子与信息学报, 2007, 29（3）: 631-634.Du Yu-ming and Yang Jian-yu. Superimposed LFM signals detection and parameter estimation based on time-frequency rate distribution[J]. Journal of Electronics & Information Technology, 2007, 29（3）: 631-634.

[15] 杜雨洺, 杨建宇. LFM 信号时间调-频斜率分布交叉项抑制方法[J]. 系统工程与电子技术, 2010, 32（2）: 229-231.Du Yu-ming and Yang Jian-yu. Elimination of cross terms of time-frequency rate of LFM signals[J]. Systems Engineering and Electronics, 2010, 32（2）: 229-231.

[16] 李利, 司锡才, 张雯雯, 等. 改进的多分量 LFM 信号参数估计算法及快速实现[J]. 系统工程与电子技术, 2009, 31（11）:2560-2562.Li Li, Si Xi-cai, Zhang Wen-wen, et al.. Improved estimation algorithm of multi-component LFM signal parameters and its fast implementation[J]. Systems Engineering and Electronics,2009, 31（11）: 2560-2562.

[17] 于媛. 基于Radon变换的LFM信号检测与参数估计[J]. 现代防御技术, 2014, 41（1）: 136-141.Yu Yuan. Detection and parameter estimation of linear frequency modulated signals based on Radon transform[J].Modern Defense Technology, 2013, 41（1）: 136-141.