托卡马克等离子体极向转动对带状流的影响

余江妹 余 俊 龚学余 谢宝艺 张 能

1（南华大学 数理学院 衡阳 421001）

2（南华大学 核科学技术学院 衡阳 421001）

托卡马克等离子体极向转动对带状流的影响

余江妹1余 俊1龚学余2谢宝艺1张 能1

1（南华大学 数理学院 衡阳 421001）

2（南华大学 核科学技术学院 衡阳 421001）

采用理想磁流体力学模型，利用绝热近似方法，推导出托卡马克等离子体极向转动体系中带状流的色散方程，分析了极向转动对带状流产生的影响。结果表明，等离子体极向转动体系下，测地声模频率和声波频率都会随极向转动马赫数而增大。带状流的频率与采用等温近似时有一定的数值差别；测地声模的密度扰动量形式也发生变化，由静态体系中纯驻波的形式，变为由一个驻波和一个小振幅行波叠加的形式。

托卡马克，带状流，频率，等离子体极向转动

在托卡马克等离子体中，带状流是一种环形和极向都对称的静电势涨落结构[1–2]。带状流有两个分支：低频带状流和测地声模。低频带状流的频率接近0，因此又称零频带状流。测地声模是带状流的高频分支，其频率ω～cs/R，其中cs为声速。广泛的理论与实验研究表明，带状流是由漂移波湍流的非线性作用激发而产生，可以从湍流中获得能量，并通过流剪切来抑制湍流所导致的反常输运[3–5]。因此带状流的研究对托卡马克聚变装置的稳态运行有着重要意义。

在带状流抑制湍流的过程中，经常会伴随着等离子体的转动，可以说，转动在托卡马克等离子体中是一种普遍存在的本质现象。对于等离子体环向转动，王少杰等[6]理论研究了等离子体环向转动对带状流的模特征的影响，结果表明，测地声模的频率和低频带状流的频率都随着环向转动马赫数而增大，且密度扰动量的形式也与静态等离子体中有所不同，由静态等离子体中的驻波变为转动体系中行波的形式。对于等离子体极向转动，其产生原因主要是强径向电场、stringer自旋加快效应以及外部动量注入等[2,7]，目前国内外的研究热点主要集中在等离子体转动对各种等离子体模的影响上[7–10]。周登[7]采用等温近似，理论研究了托卡马克等离子体极向转动体系中，带状流的频率随极向转动马赫数的变化情况。Pamela等[10]研究了等离子体极向转动体系下的边界局域模，得出了等离子体极向转动对边界局域模稳定性的影响。

本文采用理想磁流体力学模型，利用绝热近似方法，推导出带状流在极向转动体系下的色散方程。通过对色散方程的求解，得出低频带状流和测地声模频率的解析式，以及带状流频率随极向转动马赫数的变化情况，并分析得出托卡马克等离子体极向转动对带状流的影响。

1 理论模型

采用理想磁流体模型，基本方程组为：

式中，ρ、P和u分别是等离子体质量密度、压力和速度；Φ、B和j分别是电势、磁场强度和电流密度；γ是绝热系数。

在磁流体力学中，托卡马克等离子体速度的一般形式为[7]：

式中，K(ψ)和Φ'都是磁面ψ的函数。将平衡速度分成极向速度和环向速度，即，其中ˆθ和 ˆφ分别为极向方向单位矢量和环向方向单位矢量。则环向速度uT=ρ–1KBT+RΦ'，极向速度up=ρ–1KBp，这说明当等离子体极向速度存在时，环向速度必然也存在，即单纯的等离子体极向转动是不存在的，环向转动必然会伴随着极向转动而存在。本文采用文献[7]所提出的转动体系，即在环向速度中的ρ–1KBT项被另外一项RΦ'几乎抵消掉的情况下，考虑极向转动对带状流所产生的效应。

假设ρ0、p0、u0、Φ0、j0为平衡量，当体系处于静态时，式(2)可写作：

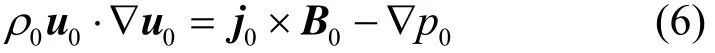
将式(2)分别乘以磁场B0和▽φ，可以得到：

将密度ρ0写作的形式，由式(7)和(8)可得：

式中，Mp=BTup/Bpcs为极向转动马赫数，cs为声速；，q为安全因子。

引入等离子体质量密度扰动量ρ1、压力扰动量p1、温度扰动量T1、速度扰动量v、静电势扰动量Φ1、电流密度扰动量j1，假设压力扰动量，等离子体比压β～ε2。

其中，式(16)为动量方程式(12)平行磁场方向的分量方程，式(17)由动量方程作磁面平均而得到。

式(15)–(18)可简化为：

2 结果分析

对式(15)进行求解，可以得出色散方程：

方程的解为：

式(28)，10ω=，为低频带状流。式(29)是由低频带状流衍生出的模，其频率随极向转动马赫数而增加，且与极向转动马赫数成简单的正比关系。式(30)中的两个解，分别表示极向转动情况下的测地声模(+)和声波(–)。

图1为绝热系数γ=5/3时，不同的安全因子下，测地声模的归一化频率随极向转动马赫数的变化情况。由图1，测地声模的频率随极向转动马赫数而逐渐增大。图2为绝热系数γ=5/3时，声波的归一化频率随极向转动马赫数的变化情况，与测地声模相类似，声波的频率也随着极向转动马赫数而逐渐增大。

由图1和图2可看出，在等离子体极向转动体系中，测地声模的频率和声波的频率与静态等离子体中有所不同，都会随着极向转动马赫数而增大。本文采用绝热近似方法，所得结果与文献[7]采用等温近似所得结论相类似，说明不论采用绝热近似，还是等温近似，在极向转动体系中测地声模和声波的频率都会随着极向转动马赫数而增大。

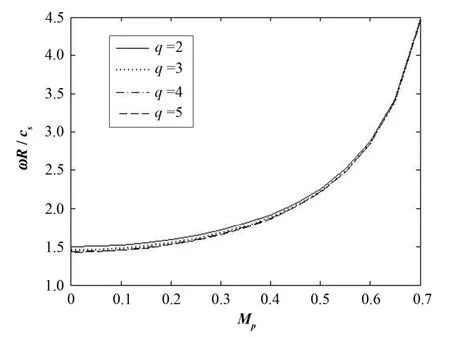
图1 GAM频率随极向转动马赫数的变化Fig.1 Frequencies of GAM plotted with respect to the poloidal Mach number.

图2 SW频率随极向转动马赫数的变化Fig.2 Frequencies of the sound wave plotted with respect to the poloidal Mach number.

但采用不同的近似方法，带状流的频率会有不同的数值结果。图3为安全因子q=5时，绝热系数γ=1和γ=5/3的情况下，测地声模归一化频率随极向转动马赫数的变化情况。图4为安全因子为5时，绝热系数取不同数值情况下，声波的归一化频率随极向转动马赫数的变化情况。由图3和图4可以看出，当绝热系数取不同数值时，即采用不同的近似方法时，测地声模频率和声波的频率都会有一定的数值差别。

图3 GAM频率变化比对Fig.3 Frequency comparison of GAM.

图4 SW频率变化比对Fig.4 Frequency comparison of the sound wave.

测地声模密度扰动量形式也发生一定的变化，与静态等离子体中有所不同。将测地声模密度扰动量写作cos部分和sin部分，这两部分之间的比值与呈一定的关系：

图5表示测地声模密度扰动量cos部分与sin部分的比值，随着极向转动马赫数的变化情况。当时，即体系处于静态时，式(31)的值为0，这表明测地声模的密度扰动量为纯驻波的形式。在等离子体极向转动体系中，由图5可看出，式(31)为一个极小的值，这与在静态等离子体体系中值为0有所不同，表明测地声模的密度扰动量为一个驻波和一个小振幅行波相叠加的形式。

图5 GAM密度扰动量cos部分和sin部分的比值Fig.5 Ratio between the cos and sin components of density perturbation for GAM.

3 结语

本文采用磁流体力学模型，绝热近似方法，理论研究了托卡马克等离子体极向转动对带状流的影响。结果表明在等离子体极向转动体系下，测地声模频率和声波频率都随极向转动马赫数而增大。采用绝热近似方法时，压力扰动量的形式与采用等温近似时的并不完全相同，因此得到的带状流频率会有数值上的差别。此外，测地声模的密度扰动量形式也与静态等离子体时有所不同，在静态等离子体中，测地声模的密度扰动量为驻波的形式，而在极向转动等离子体体系中，测地声模的密度扰动量是一个驻波和一个小振幅行波相叠加的形式。

1 Diamond P H, Itoh S I, Itoh K, et al. Zonal flows in plasma- a r eview[J]. P lasma Physics and Controlled Fusion, 2005, 47(5): R35–R50

2 Hassam A B, Drake J F. Spontaneous poloidal spin-up of tokamak plasmas: reduced equations, physical mechanism, and sonic regimes[J]. Ph ysics Plasmas, 1993, 5(11): 4022–4029

3 Yu J, Gong X Y. Geodesic acoustic mode excitation by drift waves in tokamak plasmas with toroidal rotation[J]. Nuclear Fusion, 2013, 53(12): 123027

4 Yu J, Gong X Y, Chen Y. Lo w frequency zonal flow excitation by drift waves in tokamak plasmas with toroidal rotation[J]. Nuclear Fusion, 2015, 55(2): 023015

5 Guo W F, Wang S J, Li J G. Damping effects of finite parallel thermal conductivity o n zonal f lows[J]. Plasma Physics and Controlled Fusion, 2008, 50(9): 095006

6 Wang S J. Zonal flows in tokamak plasmas with toroidal rotation[J]. Physical Review Letters, 2006, 97(8): 085002

7 Zhou D. Zon al flow modes in a tokamak plasma with dominantly poloidal mean f lows[J]. Phy sics Pla smas, 2010, 17(10): 102505

8 Elfimov A G, Galvao R M O, Sgalla R J F. Rotation effect on geodesic and zonal f low modes in tokamak plasmas with isothermal magnetic surfaces[J]. Plasma Physics and Controlled Fusion, 2011, 53(10): 105003

9 Elfimov A G. Alfvén continuum deformation by kinetic geodesic ef fect in rotating tokamak plasmas[J]. Ph ysics Plasmas, 2010, 17(2): 022102

10 Pamela S, Huysmans G, Benkadda S. Influence of poloidal equ ilibrium rotat ion i n MHD simulations of edge-localized modes[J]. Plasma Physics and Controlled Fusion, 2010, 52(7): 075006

CLC TL61+2.4

Effects of poloidal rotation on zonal flows in tokamak plasmas

YU Jiangmei1YU Jun1GONG Xueyu2XIE Baoyi1ZHANG Neng1
1(School of Mathematics and Physics, University of South China, Hengyang 421001, China)
2(School of Nuclear Science and Technology, University of South China, Hengyang 421001, China)

Background: Zonal flows are the electrostatic modes with structures of toroidal symmetry and poloidal symmetry, which play an important role in restraining turbulences. In the process of turbulence suppression, the poloidal rotation widely exists in tokamak plasmas. Purpose: In this study, the effects of the poloidal rotation on zonal flows in tokamak plasmas are concluded. Methods: With the dispersion relation derived by using ideal MHD model with the adiabatic approximation, the frequencies of zonal flows are deduced. Results: Firstly, the frequency of the geodesic acoustic mode (GAM) increases with respect to the poloidal Mach number when adiabatic coefficient is 5/3. Secondly, the frequency of the sound wave (SW) increases with respect to the poloidal Mach number when adiabatic coefficient is 5/3. Third ly, the frequency of GAM with γ=1 i s dif ferent from th at when γ=5/3. Th e fourth, the frequency of SW with γ=1 is different from that when γ=5/3. The last, the ratio between the cos and sin components of density perturbation for GAM is a very small value in the poloidally rotating plasma. Conclusion: It is shown that the frequencies of the zonal flows with the adiabatic approximation, increase with respect to the poloidal Mach number, but differ in numerical value of the frequencies of the zonal flows with the isothermal approximation. In contrast to the pure standing wave form in static plasmas, the density perturbations consist of a standing wave superimposed with a small amplitude traveling wave in the poloidally rotating plasma.

Tokamak, Zonal flows, Frequency, The poloidal rotation of plasmas

TL61+2.4

10.11889/j.0253-3219.2015.hjs.38.100602

No.11105071、No.11375085、No.11475083、No.41104094、No.11405082)、南华大学核聚变与等离子体物理创新团队(No.NHXTD03)资助

余江妹，女，1989年出生，2012年毕业于洛阳师范学院，现为南华大学硕士研究生，研究领域为核聚变与等离子体物理

2015-06-19，

2015-08-23