复杂孔隙结构储层变岩电参数饱和度模型研究

罗少成，成志刚，林伟川，姜微微，肖飞，唐冰娥

（1．中国石油集团测井有限公司油气评价中心，陕西 西安710077；2．中国石油集团测井有限公司长庆事业部，陕西 西安710021）

0 引 言

饱和度评价是油气储集层定量评价的核心［1］，饱和度求取最常用的方法是测井解释法，其基本依据为Archie公式［2］，其中重要参数岩性系数、胶结指数和饱和度指数的取值对于饱和度的计算结果有很大影响，合理选择这组参数至关重要，对于复杂孔隙结构储层更是如此［3］。传统Archie公式在复杂孔隙结构的低孔隙度低渗透率储层适应性差，区域固定的岩电参数计算含油饱和度偏低，需重新建立与之适应的饱和度方程，难度很大［4］。在已有饱和度方程大致适应复杂孔隙结构的低孔隙度低渗透率储层的基础上，仅对其中参数进行适应的修正，可以较好地控制饱和度计算精度。

××油田复杂砂岩储层的岩性为岩屑长石砂岩和长石岩屑砂岩；储层类型以长石溶孔为主，粒间孔相对不发育；储层孔隙度主要分布在3%～10%，平均孔隙度7．69%，渗透率主要分布在（0．01～0．1）×10－3μm2，平均为0．093×10－3μm2。储层非均质性强，物性变化大，14口井130块岩心岩电分析实验统计结果表明，岩性系数a、胶结指数m和饱和度指数n值的变化范围大。为了更准确地定量评价储层，本文对Archie公式中的参数进行了深入分析，建立了变岩电参数a、m和n的饱和度修正模型，提高了解释精度。

1 地层因素F与孔隙度φ的关系

复杂孔隙结构砂岩储层的F－φ关系较中高孔隙度渗透率储层复杂。图1为研究区14口井130块岩样的地层因素F与孔隙度φ的关系图。测量条件：岩样饱和50g／L的CaCl2溶液，测量温度25℃，湿度70%。对测量数据进行拟合，拟合关系为：F＝5．2397／φ1．1099，R＝0．8992，具有低m高a的特征，与理论值相差很大，表明了目的层地层因素模型的复杂性。从图1可见，F与φ在双对数坐标系下在孔隙度为9%时具有明显的分段性，不能简单地用阿尔奇公式描述。孔隙度大于9%时

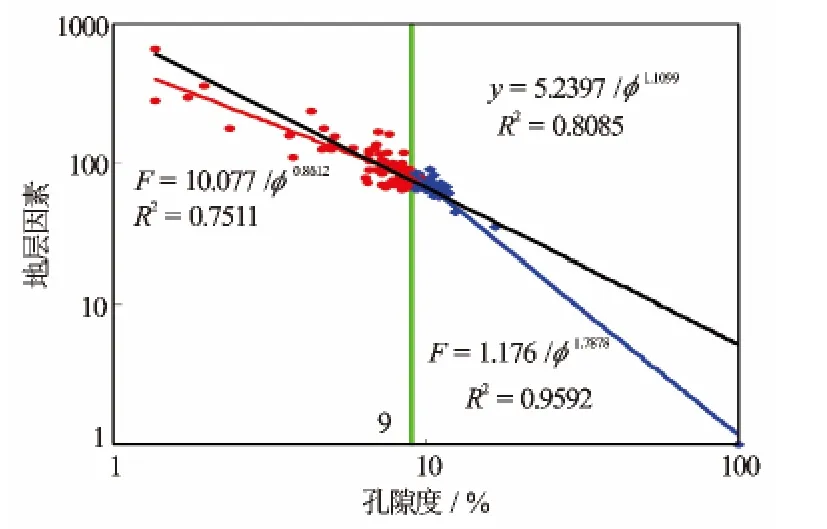
图1 地层因素与孔隙度关系图

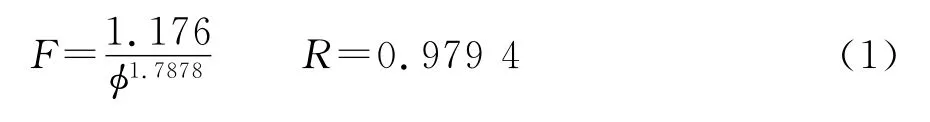
孔隙度小于9%时

1．1 岩性系数a和胶结指数m的关系

对研究区14口井130块岩心岩电实验资料进行分区统计，确定了不同井区岩性系数a和胶结指数m值，对a和m值进行统计分析，发现a与m具有很好的相关性，呈幂函数关系（见图2），其表达式为

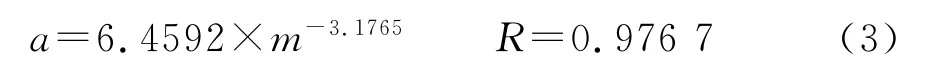
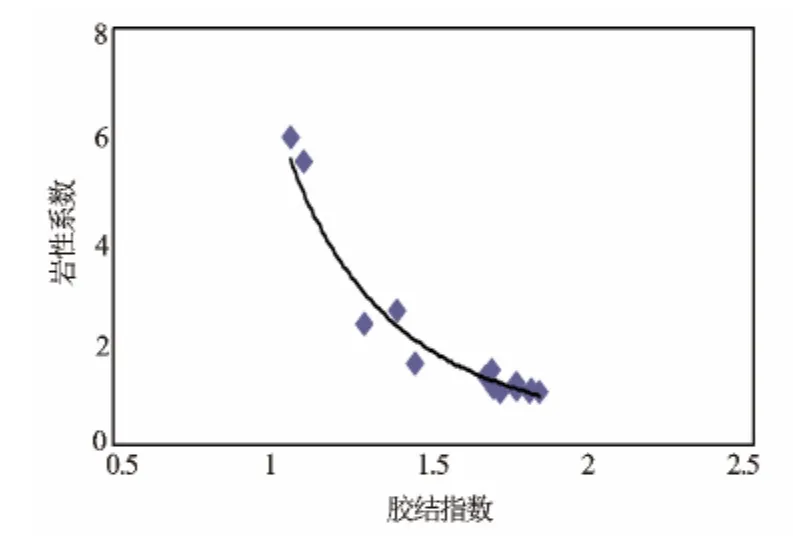
图2 岩性系数与胶结指数关系

从图2可见，a和m不是2个孤立的值，两者之间相互制约。即当m增大时，a值减小；m减小时，a值增大。且m和a值的变化范围较大，m值集中在1．05～1．83之间，a值集中在1．0～5．92之间。只有当m＝1．7左右时a接近于1，表明将a近似为1，与实验分析结果不符。

1．2 m值的确定

联立式（1）和阿尔奇公式F＝a／φm可确定单块岩心的a和m，但由于两式均为非线性方程，求解不具备唯一性。已有实验证明在双对数坐标系下地层因素F是孔隙度φ的二次函数的，F与φ存在普遍的非线性关系［5］。对实验点进行不同数理统计分析，地层因素与孔隙度在lgF－lgφ坐标系下，用三次函数关系拟合可以将整套实验数据统一起来，其相关性最好，曲线走向更符合实验点的趋势（见图3），其三次函数关系式为

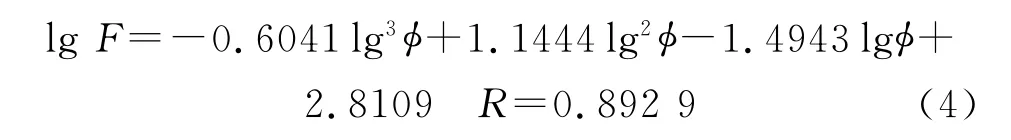
式中，φ为孔隙度，%。

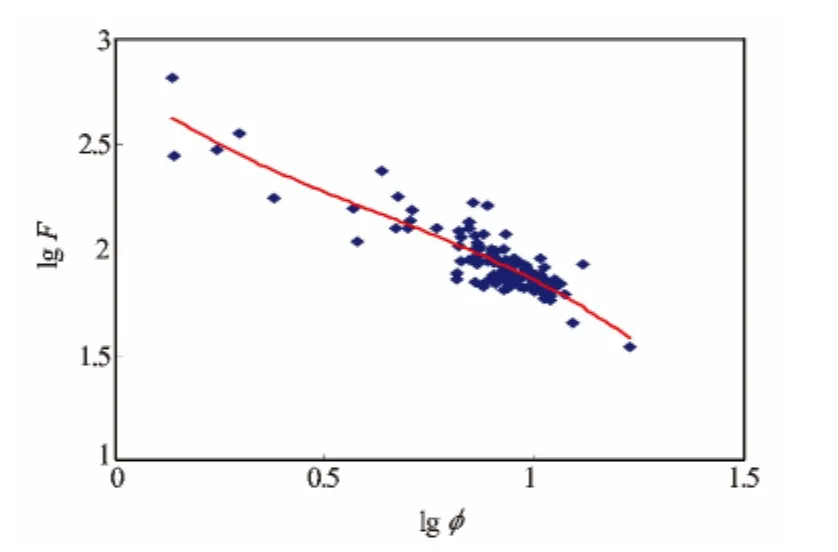
图3 lg F与lgφ的关系

式（2）的一般形式为

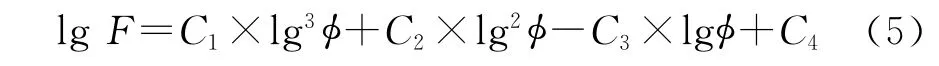
对式（3）进行变形得

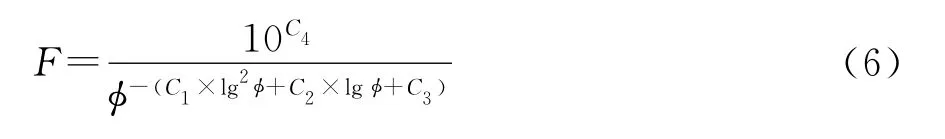
将式（6）和F＝a／φm对比，a值可通过图2所揭示的关系求得，m为

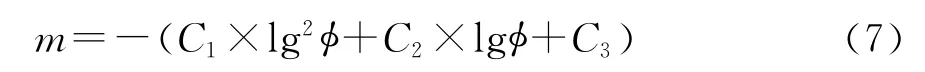
式（7）表明，m和φ之间存在相互制约的关系，即通过式（7）可确定随储层变化而变化的m值。对图1所示实验数据，联立式（3）和式（7），结合阿尔奇公式，以岩石导电效率为约束条件［6］，采用最小二乘法求得式（7）中的待定系数C1、C2和C3，建立变m模型

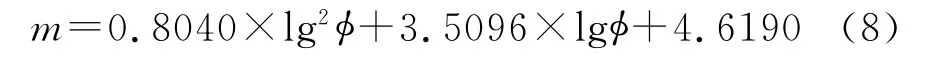
式中，φ为孔隙度，%。从模型表达式的结果看，孔隙度主要分布在3%～10%，m值分布在1．1410～1．9143，m值的分布是合理的。

2 电阻率增大率I与含水饱和度Sw关系及n值的确定

2．1 电阻率增大率与含水饱和度的关系

图4为研究区电阻率增大率与含水饱和度关系图。实验数据点在Sw＝90%存在明显的拐点，说明通过同一区块岩电数据回归的饱和度指数n值并不是唯一的一个值，n值的固定只适用于Sw在一定的范围内。对所有实验样品点采用阿尔奇模型进行回归，误差较大，表现为非阿尔奇岩石特征。以Sw＝90%为界限，当Sw分别小于90%和为90%～100%时，lgI和lgSw均表现出很好的线性相关性，其表达式为，当Sw＜90%时

当Sw≥90%时

从式（9）和式（10）看，2条直线的特征明显不同，该现象说明高含水饱和度和中低含水饱和度情况下，岩石的导电特征有差异。岩电实验中，随着含水饱和度的降低，岩石中的大孔隙喉道逐渐被几乎不导电的物质取代，导电流体主要存在于小的喉道中，此时岩石电阻率主要受孔隙曲折性的控制。岩石的非均质性越强，孔隙结构越复杂，岩石电阻率越高。孔隙结构的非均质性特点导致Rt／Ro不随Sw呈简单的函数变化，反映到lgI和lgSw交会图上，二者不再是简单的线性关系。

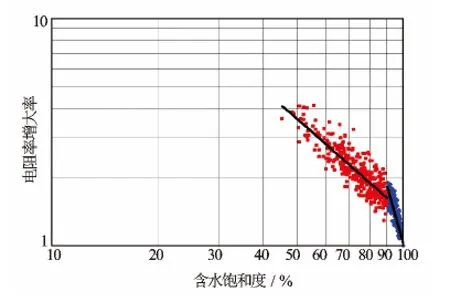
图4 电阻率增大率和含水饱和度关系图

2．2 n值的确定

通过I－Sw之间的数学关系对研究区130块岩样进行单样品的拟合求取130组b和n值。在不同孔隙度渗透率条件下，绝大部分岩样的b值基本趋近1。从理论上讲，岩石完全含水时（Sw＝100%）相应的电阻率增大率I等于1，由岩石电阻率Rt与含水饱和度Sw的关系I＝Rt／Ro＝b／Snw知，b值都应等于1。为此，令b＝1，对130块岩样的电阻率增大率I与含水饱和度Sw实验数据重新进行拟合确定出每块岩样的饱和度指数n。

岩石的非均质性越强，孔隙结构越复杂，岩石电阻率越高。已有实验证实，储层岩石的孔隙结构是影响饱和度指数n的最主要因素［7］。核磁共振测井是确定储层孔隙结构最有效的测井方法［8］。饱和度指数n可由核磁共振实验数据分析确定。

T2截止值将总孔隙度对应的T2谱分布分成小孔径和大孔径2部分，即不可动流体和可动流体。不可动流体孔隙度φb为小于截止值所对应的T2孔隙度分量的累加；可动流体孔隙度φm为大于截止值所对应的T2孔隙度分量的累加。φb／φm值越大，说明储层孔隙中小孔隙所占比例越多，储层的孔隙结构越复杂。建立了饱和度指数n和不可动流体孔隙与可动流体孔隙比值的统计关系，饱和度指数n随φb／φm的增大而增大，即孔隙结构越复杂，n值越大，其统计关系为

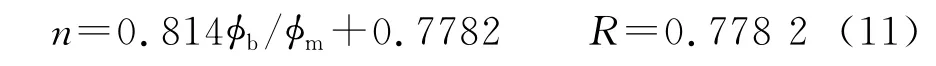
式中，n为饱和度指数，无因次；φb为不可动流体孔隙度，%；φm为可动流体孔隙度，%。

T2几何平均值（T2，gm）与储层孔隙结构密切相关，随孔隙结构变化而变化，是刻画孔隙结构十分有效的参数。在不考虑油气对T2谱影响的前提下，由核磁共振测井与岩电的配套实验可建立饱和度指数n与T2几何平均值T2，gm之间关系

岩石的孔隙结构制约着储层的孔隙度和渗透率。由于致密储层很难准确计算渗透率，建立了饱和度指数n与孔隙度φ的关系。从统计结果显示，饱和度指数n与孔隙度φ存在一定的相关性，其表达式为

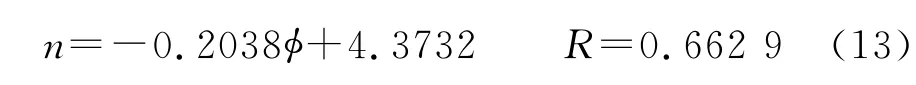
根据上述实验数据分析，油藏条件下的含水饱和度指数n值与任一单因素的相关性都不是特别好，即用单因素进行回归，必定存在较大的误差。因此，提出采用多因素对饱和度指数n进行拟合（见图5），精度得到了提高，其模型公式为

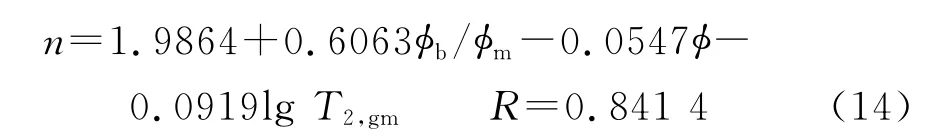
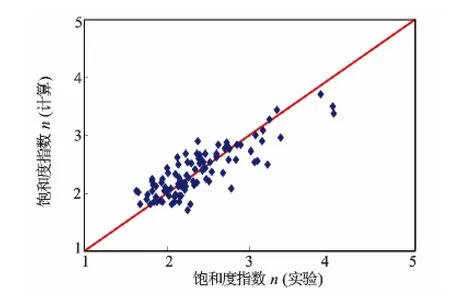
图5 计算n值与测量n值对比图

3 实例及应用效果评价

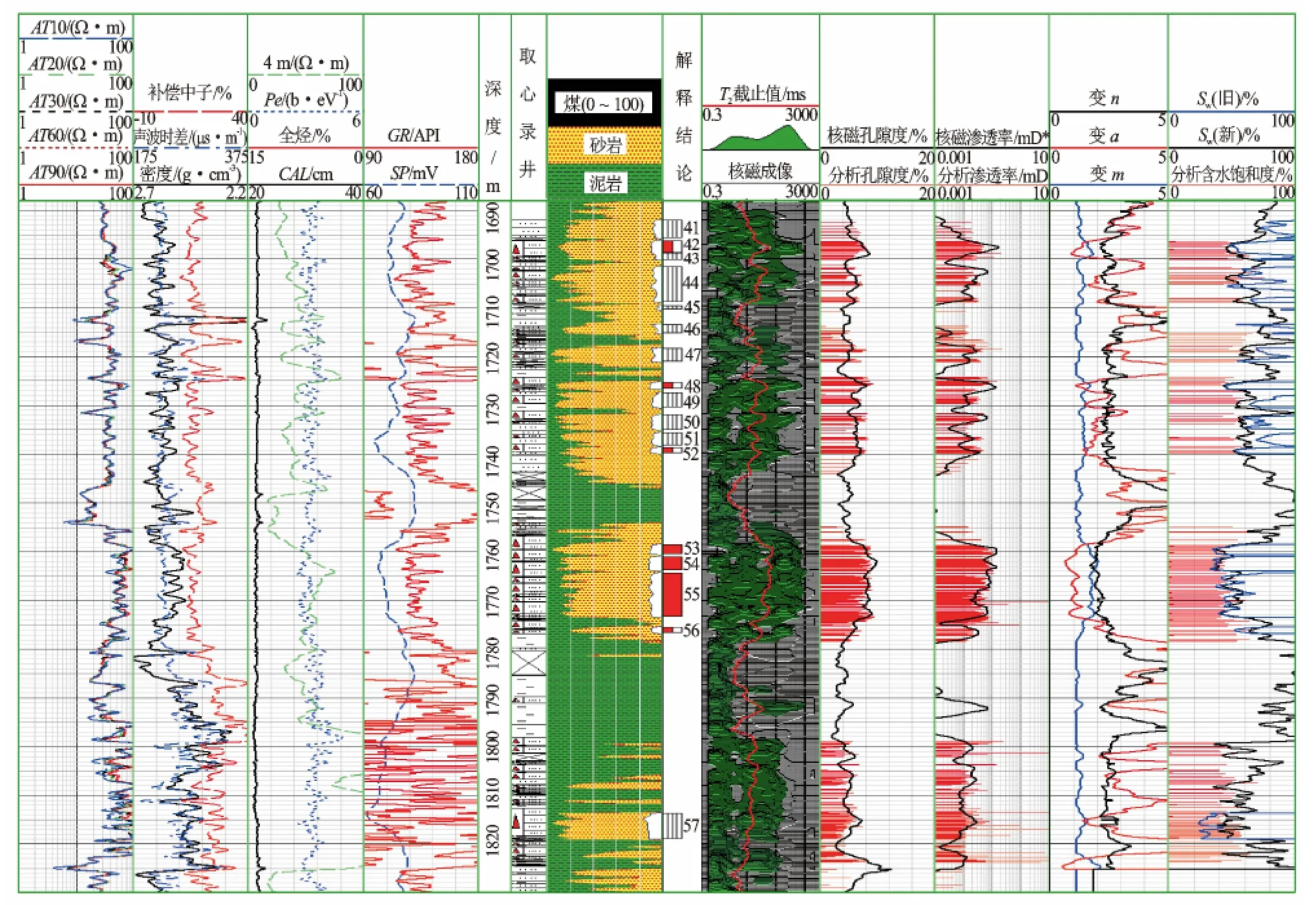
图6 A井计算含水饱和度与分析含水饱和度对比图

图6为A井计算含水饱和度与岩心分析含水饱和度对比图。图6中第9道为核磁共振测井T2谱和计算的变T2截止值，第10道和11道红色杆状条为岩心分析孔隙度和渗透率，黑色线为计算的孔隙度和渗透率，第12道为计算的变岩电参数a、m和n，第13道红色杆状线为岩心分析校正后的含水饱和度值，蓝色曲线为传统阿尔奇公式（区域固定的a、b、m和n）计算含水饱和度，黑色曲线为变a、m和n计算含水饱和度。

从图6可见，传统阿尔奇公式计算含水饱和度偏高，变岩电参数饱和度修正模型计算含水饱和度与岩心分析值一致性好。为了更加形象地说明饱和度计算的准确性，按取心段分段计算了饱和度的绝对误差和相对误差（见表1），利用传统阿尔奇公式计算含水饱和度总的平均相对误差达到了17．24%，利用变岩电参数饱和度修正模型计算含水饱和度总的平均相对误差为6．63%，解释精度提高了10%，满足了储量计算的误差要求。

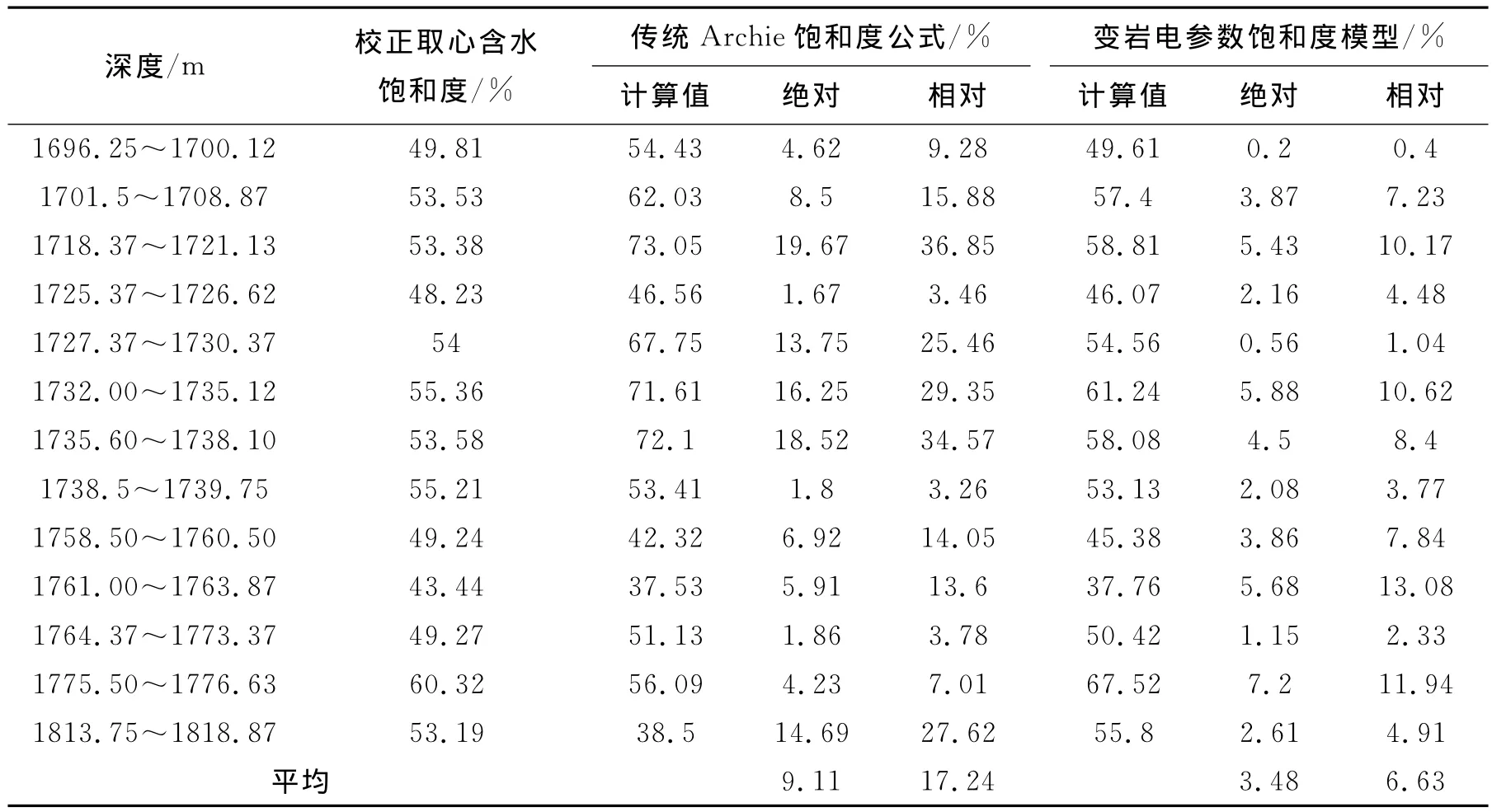
表1 饱和度计算误差的对比分析表

4 结 论

（1）研究区实际资料表明，地层因素与孔隙度关系复杂，具有低m高a的特征，与理论值相差很大。不同井区的a和m值分布范围广，且两者之间相互制约，呈幂函数关系，m与lgφ存在一元二次函数关系。

（2）储层岩石的孔隙结构是影响饱和度指数的最主要因素，孔隙结构越复杂，饱和度指数n越大。结合岩心核磁共振T2谱，采用多因素拟合方法建立饱和度指数n值计算公式。

（3）采用的变岩电参数a、m和n修正了饱和度解释模型，实际应用效果比较好，解释精度比传统的阿尔奇方法提高了10%以上，满足了储量计算误差要求，有效克服了传统阿尔奇模型在复杂孔隙结构储层中的不适应性。

［1］孙建孟，王克文，李伟．测井饱和度解释模型发展及分析［J］．石油勘探与开发，2008，35（1）：101－107．

［2］Archie G E．The Electrical Resistivity Log as an Aid in Determining Some Reservoir Characteristics［J］．Trans AIME，1942，146：54－61．

［3］孙小平，石玉江，姜英昆．复杂孔隙结构储层含气饱和度评价方法［J］．天然气工业，2000，20（3）：41－44．

［4］中国石油勘探与生产分公司．低孔低渗油气藏测井评价技术及应用［M］．北京：石油工业出版社，2009．

［5］毛志强．油藏条件下饱和度测井解释基础实验、理论和应用研究［D］．北京：中国石油勘探开发研究院，1995．

［6］HerrickD C，Kennedy W D．Electrical Efficiency——A Pore Geometric Theory for Interpreting the Electrical Properties of Reservoir Rocks［J］．Geophysics，1994，59（6）：918－927．

［7］李奎周，葛新民，汪海龙，等．基于实验条件下的低孔低渗岩心饱和度指数影响因素研究［J］．特种油气藏，2011，18（3）：35－38．

［8］肖立志．核磁共振成像测井与岩石核滋共振及应用［M］．北京：科学出版社，1998．