独立评分考生成绩统计量模型的构造

2015-12-11田俊忠

湖南师范大学学报·自然科学版 2015年6期

通讯作者，Email：hn_syb@126.com（北方民族大学基础教育学院，中国银川750021）

摘要如何综合阅卷教师的独立评分，科学合理地确定考生的成绩，是主观性评价网上阅卷的关键问题之一.提出了考生获得各个分数值的难度系数的新概念，认为考生试卷成绩的确定不能是简单的平均值，应该是考虑分数值难度系数的加权平均，根据随机独立专家评分构造了高考作文网上阅卷考生成绩的统计量模型.该模型对于各种类型的主观性评价网上阅卷的成绩确定具有广泛的应用.

关键词难度系数;成绩统计量;一致最小方差无偏估计;数学模型

中图分类号O212.2文献标识码A文章编号10002537（2015）06006805

On the Construction of Statistical Estimation

of the Teachers Independent Score

TIAN Junzhong*

（College of General Education， Beifang University of Nationalities， Yinchuan 750021， China）

AbstractHow to calculate teachers independent score scientifically and reasonably determine the examinees score， is a key issue in the subjective evaluation of the online marking. The new concept of the difficulty coefficient that the examinee obtain each score was proposed. It is considered that the examinees score can not be a simple average， it should be the weighted average of the difficulty coefficient. Based on its randomness and independence， the statistical estimation model of the examinees score of online marking was constructed. The model has a wide practical application for all kinds of subjective evaluation of online marking.

Key wordsthe coefficient of the difficulty; statistical estimation of the score; uniformly minimum variance unbiased estimation; mathematical model

主观性评价网上阅卷（如高考作文网上阅卷）的工作流程与计算机技术日益成熟，使用范围不断地扩大，目前全国各个省份都实行了网上阅卷[1].阅卷系统向阅卷教师随时随机分发评阅试卷，电子化的试卷完全消去了考生的个人信息.在整个评分过程中，阅卷教师在时间上和空间上是分离的，工作上都相互独立，他们互不影响，工作流程的管理办法保证了阅卷老师独立自主地认真评阅，所以任何一位评卷人员对任何一篇电子化评阅作文的评分都是相互独立的.

由于电子试卷的随机分发，每一份试卷在整个阅卷期限内、在任何时间上都有同等的概率分发到每位阅卷教师; 电子化的评阅作文还可以多次分发，可以在同一时间发给不同教师，也可以在不同时间分发给不同的教师.不同的阅卷人员在评阅同一份电子化的评阅作文是有差异的，为了消除阅卷教师在对评分标准的理解、对叙述问题方式的喜好、评阅时的工作态度与心理倾向等方面的系统偏差，在组织管理中对阅卷教师进行严格选拔，他们都是长期从事本专业教学和研究的高级教师，多次参加此类型试题的网上阅卷，在评卷之前认真组织培训，充分讨论评分标准，模拟评卷，规范评卷行为，统一基调，使阅卷评分更加趋同[25].

由于评阅作文是一种主观性评价，阅卷专家的评分受个人的知识业务水平、教学工作经验积累、对评分标准的理解把握、对叙述问题方式的喜好、评阅时的工作态度、对题材的心理倾向以及持续工作的抗疲劳能力等等方面的影响较大，使得不同的评卷人员在经过培训之后仍然对同一篇作文主观性评价的评分往往有一定的差距[67].所以主观性评价网上阅卷在数学上存在着一个关键性的问题：那就是如何确定一份试卷的考试成绩，如何综合各位阅卷老师的独立评分，本文以高考作文网上阅卷为背景，研究构造给出主观性评价网上阅卷独立评分考生成绩统计量的数学模型.

1问题的提出

设X=^一份电子化的评阅作文的评分.由于评阅专家是随机抽取的，则X是随机变量，E（X）=μ是评阅试卷水平的真值，是未知待估的.若在全体阅卷老师专家集合中随机抽取n个专家对同一篇作文进行网上独立评分，得样本X1，X2，…，Xn，由辛钦大数定理可知，其算术平均值=1n∑nk=1Xk以概率收敛到其真值μ上，且是μ的一致最小方差无偏估计[89]，所以，只要n充分大，在大样本下，一般取作为μ的估计量，就可以作为该试卷的成绩.

湖南师范大学自然科学学报第38卷第6期田俊忠：独立评分考生成绩统计量模型的构造然而在实际工作中n不可能充分大，由于阅卷时间、阅卷人数和阅卷强度等方面的限制，一份试卷往往进行两评、三评（为了验证某些疑点，在特殊情况下极少量的电子作文才有四评），在这种情况下如何根据一份试卷的两评或三评的评分来确定它的考试成绩.十几年来，实际工作中为了简便易行便于操作，凭经验确定了一个误差控制限A，设X1与X2分别是随机的两位评卷教师对同一评阅材料的评分，若|X1-X2|≤A，则该试卷的成绩为Y=X1+X22，若|X1-X2|>A，则由阅卷系统自动随机地从评卷教师专家集合中再随机地抽取一位专家进行独立的评阅，设评分为X3，若|X1-X3|<A，则该试卷的成绩为Y=X1+X32，若|X2-X3|<A，则该试卷的成绩为Y=X2+X32.否则，由阅卷组长负责另行集体讨论处理.

这种确定成绩的方法实际上是在评阅专家集合中随机搜寻相近的两位专家，取他们评分的简单平均值作为考生的成绩.由于试卷随机地分发，等可能地分发到每一位专家的手中，如果两位专家的意见有较大的不一致性，那么随机碰到的第三位专家的评分基本上左右了该试卷成绩的高低.比如：为了使得三评量不要太大，取误差控制线A等于10，如果对于一份试卷的两评评分分别为X1=56与X2=36，那么就有|X1-X2|>A，于是随机分发到第三位专家进行三评，当碰到的一个专家独立评分给出的三评评分X3=50时，则该试卷的成绩为Y=X1+X32=53，当碰到的是另一个专家独立评分给出的三评评分X3=30时，则该试卷的成绩为Y=X2+X32=33，所以，该份试卷的成绩的高低基本上是由进行三评时究竟遇到什么样的专家水平来决定，这样，不论该份试卷的水平如何，这种确定方法使得该份试卷的考生要么吃亏，要么占便宜，总之是不公平的，也是不公正的，而且随着误差控制线A的缩小，三评的试卷份数将会增加，这种情况形成的不公平的数量也随着增加，扩大了不公平的考生数量，本来缩小误差控制线A，应该有利于缩小不公平的数量，但适得其反，成绩的这种计算方法是有问题的，更何况取算术平均作为真值的估计，其基本前提是大样本才行，因此需要深入研究网上阅卷成绩确定这一世界性难题.

2分值的难度系数

根据两评的成绩X1与X2或三评的成绩X1，X2，X3来计算考生的得分成绩时，考生成绩Y不仅取决于评阅教师的评分Xi（i=1，2 或i=1，2，3），而且也应该注意到这样一个因素，由于种种原因，阅卷教师评分的趋中现象是个不合理的常态，是难以避免的评阅现象[1011].越是给出很高分或者很低分，评阅教师越是很慎重，所以，考生获得此分值的难度就越大，若要获得较高的评分，说明考生的综合素质水平比较高、综合能力比较强，在确定考生成绩时应该加大其权重;反之，一般性的综合素质水平与能力，其基本要求绝大多数考生容易做到，阅卷教师给出评分很低的分值也是比较困难的，意味着考生获得很较低的难度系数也较高.因而处在不同的分数段则有不同的难易程度度，阅卷教师评分的分值不同，则其得分的难度程度也是不同的.

我们假定阅卷教师队伍几年来相对稳定和成熟，这可以通过组织领导、组织管理与工作总结讨论学习在实际工作中能够实现，那么，可以通过几年的数据来测定各个分值的难度程度.

设f（x）是分值x的考生人数占全部考生人数的比重，由于说明高考作文试卷设定的满分为60.则 0≤x≤60，实际上，f（x）是分值x的统计频率.如果设考生总数为N，即评阅试卷的总份数为N，那么分值为x的考生人数为Nf（x） .

定义1对于任意的分值x， 0≤x≤60，则称

F（x）=11+f（x）（1）

为分值x的难度系数，其中，f（x）=分值x的考生人数N .

从中可以看出，考生获得分值x的难度系数与分值为x的考生人数所占总人数的比例成反比，那个分值上的试卷份数最多，或考生人数最多，则该分值的难度系数最小.从统计的意义上看，一般来说，考生获得高分的难度较大，获得低分的难度也较大，同时，在长期的阅卷工作实践中，从阅卷的主观性评价上看，阅卷教师给出高分的难度较大，给出低分的难度也较大，如果一个阅卷教师确实给出了高分或低分，它是经过斟酌评分标准尺度与作文内涵水平，慎重评阅给出的，其评分更加接近于该作文的实际水平.显然，难度系数F（x）是有界的，且0<F（x）<1 ，它反映了一个考生获得阅卷教师评分分值x的难易程度， F（x）越大，说明获得分值x的难度较大，反之亦然.

3考生成绩统计量模型的构造

由于阅卷教师精心挑选、长期实践培养、严格培训与不断总结经验，每一位阅卷教师都能把握标准，能够做出准确判断，同时在评分时互不影响，相互独立，所以每一位阅卷教师的评分都反映了考生的某些信息，无论是两评还是三评，考生的成绩不应该是简单的算术平均，应该更为全面，取它们的加权平均比较合理.权重以获得该分值的难度系数为依据，来进行考生成绩统计量的构造.

设X1，X2，X3是随机抽取的三位阅卷教师的网上阅卷的评分，X1，X2，X3是独立同分布的随机变量，且都服从正态分布[12]，考虑构成考生成绩的数学结构是线性的.设βi（i=1，2，3）为Xi的系数，于是确定考生成绩的数学结构为

Y=β1X1+β2X2+β3X3，（2）

其中，β1+β2+β3=1.

考虑系数大小βi（i=1，2，3）只与它们各自的难度系数F（Xi）有关，

若Xi的难度系数F（Xi）越大，则βi应该越大，即Xi对于考生成绩Y的贡献较大，反之亦然.于是令 βi=kF（Xi），且 β1+β2+β3=1，

于是得： k=1F（X1）+F（X2）+F（X3），

那么，考生成绩的表达式结构为

Y=F（X1）F（X1）+F（X2）+F（X3）X1+F（X2）F（X1）+F（X2）+F（X3）X2+F（X3）F（X1）+F（X2）+F（X3）X3.（3）

由于X1，X2，X3是随机变量，是阅卷教师评分X（它是一个正态总体）的一个样本，Y是样本X1，X2，X3的一个函数，不含有任何未知参数，所以Y是一个统计量，它是考生成绩的一个估计量.

如果 |X1-X2|≤A，则没有三评评分，即X3与F（X3）都不存在，

所以两评条件下考生成绩统计量为

Y=F（X1）F（X1）+F（X2）X1+F（X2）F（X1）+F（X2）X2. （4）

4模型的应用

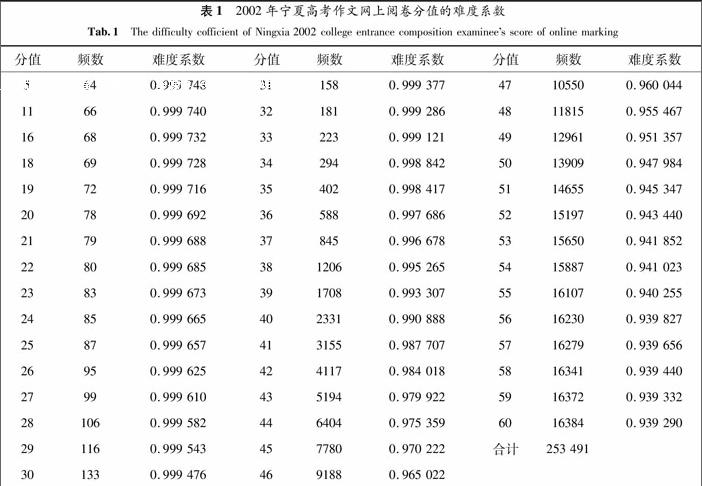
根据难度系数式（2），利用2002年宁夏高考作文网上阅卷数据，经计算得到不同分值x的难度系数F（x）的值，

表12002年宁夏高考作文网上阅卷分值的难度系数

Tab.1The difficulty cofficient of Ningxia 2002 college entrance composition examinees score of online marking

分值频数难度系数分值频数难度系数分值频数难度系数5640.999 748 311580.999 377 47105500.960 044 11660.999 740 321810.999 286 48118150.955 467 16680.999 732 332230.999 121 49129610.951 357 18690.999 728 342940.998 842 50139090.947 984 19720.999 716 354020.998 417 51146550.945 347 20780.999 692 365880.997 686 52151970.943 440 21790.999 688 378450.996 678 53156500.941 852 22800.999 685 3812060.995 265 54158870.941 023 23830.999 673 3917080.993 307 55161070.940 255 24850.999 665 4023310.990 888 56162300.939 827 25870.999 657 4131550.987 707 57162790.939 656 26950.999 625 4241170.984 018 58163410.939 440 27990.999 610 4351940.979 922 59163720.939 332 281060.999 582 4464040.975 359 60163840.939 290 291160.999 543 4577800.970 222 合计253 491301330.999 476 4691880.965 022 由于相邻两年全省的高考分数值的难度系数变化很小，我们以上年的难度系数作为当年的难度系数，比较合理的难度系数应该取近三年全省难度系数的平均值作为当年的难度系数.根据成绩确定的数学模型（3）和（4），由招办随机抽取2003年宁夏高考作文网上阅卷的16份样本试卷，分别计算两评与三评时考生成绩的模拟值，并与历史成绩进行对比，分析说明其数学模型的合理性.

随机抽取16份样本试卷，两评与三评样本试卷各8份，将根据（3）和（4）来计算其模拟成绩，并与历史成绩进行对比，其结果由表2和表3给出.

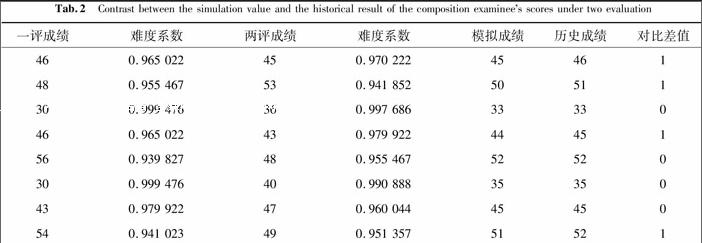
表2两评时考生成绩的模拟值与历史成绩对比

Tab.2Contrast between the simulation value and the historical result of the composition examinees scores under two evaluation

一评成绩难度系数两评成绩难度系数模拟成绩历史成绩对比差值460.965 022450.970 22245 46 1480.955 467530.941 85250 51 1300.999 476360.997 68633 33 0460.965 022430.979 92244 45 1560.939 827480.955 46752 52 0300.999 476400.990 88835 35 0430.979 922470.960 04445 45 0540.941 023490.951 35751 52 1

表3三评时登录成绩的模拟值与历史成绩对比值

Tab.3Contrast between the simulation value and the historical result of the composition examinees scores under three evaluation

一评成绩难度系数两评成绩难度系数三评成绩难度系数模拟成绩历史成绩对比差值350.998 417530.941 852430.979 92243 39 4 500.947 984380.995 265490.951 35746 50 4 520.943 440360.997 686480.955 46745 50 5 360.997 686490.951 357420.984 01842 39 3 440.975 359550.940 255400.990 88846 42 4 530.941 852360.997 686550.940 25548 54 6 520.943 440400.990 888400.990 88844 40 4 540.941 023400.990 888370.996 67843 39 5 当时根据经验判断，评分误差控制限A取为10分，当 |X1-X2|<A时，不再进行三评，两评样本试卷的历史成绩是凭经验使用简单平均公式Y=X1+X22来计算的.从表2、表3中可以看出：二评时，考生成绩的模拟值与历史成绩相比，当|X1-X2|越小，则模拟值与历史成绩越接近，或者相等.在这种情况下，考虑或者不考虑这两个评分的难度系数F（X1）与F（X2），对考生成绩影响不大，即：根据公式（3）及其推论（4）计算模拟值与历史成绩值相比较，是基本一致的，这说明了公式（3）与（4）的合理性.三评时，样本试卷的模拟成绩与历史成绩相比较，暴露了经验做法的不合理性.历史成绩的计算是招办凭经验给出，由于 |X1-X2|≥A，若|X1-X3|≤|X2-X3|成立，则使用简单平均公式Y=X1+X32来计算.反之，则使用简单平均公式Y=X2+X32来计算，可以看出上述计算公式不妥，尤其是X1，X2，X3当中有一个大于50，更为不妥，在大量的阅卷工作中，由主观经验给出的考生成绩计算公式所产生比较广泛的不公平性没有被发现，建议主观性评阅网上阅卷成绩的计算公式应采用（3）给出的计算公式，使考生的成绩更加合理化.

参考文献：

[1]罗友花，刘铁明.网上阅卷研究述评[J].中国考试，2009（11）：3437.

[2]贾志先.基于谱聚类的网上阅卷质量控制研究[J].智能计算机与应用， 2014，4（5）：7679.

[3]曹建莉，张强.评卷质量监控模型及其统计分析[J].统计与决策， 2012，18（1）：2931.

[4]肖广. 大规模教育考试中网上阅卷的实施与思考[J].考试研究， 2009，9（1）：4850.

[5]葛丽萍，李传智. 基于Web的网上阅卷系统的研究[J].科技信息， 2007，11（2）：126127.

[6]刘素梅. 俄语测试网上阅卷系统与主观题的误差控制[J].中国俄语教学， 2007，26（2）：5356.

[7]仲轶宏. 基于B/S模式的网络阅卷系统的设计与实现[D].成都：电子科技大学， 2013.

[8]陈希孺.高等数理统计学[M].合肥：中国科学技术大学出版社， 1999.

[9]LEHMANN E L， ROMANO J P. Testing statistical hypotheses （third edition）[M]. New York： Springer， 2005.

[10]彭恒利，俞韫烨.主观性试题网上评阅趋中评分控制研究初探[J].中国考试.测量与评价， 2013，（6）：39.

[11]王海. 基于Web Services 的网上阅卷系统的设计与实现[D].上海：华东师范大学， 2006.