浅述离子交换动力学模型及其机理

高教成 徐兰云

摘 要：离子交换是一种属于单元传质分离、可逆的等量交换反应过程。该文浅述了离子交换动力学模型（拟均相扩散模型、缩核模型和其他模型）考虑的因素及其应用范围，并介绍了离子交换机理（包括离子交换膜选择透过性理论和离子交换过程控制步骤）。离子交换膜选择透过性理论可采用双电层理论或Donnan膜平衡理论来解释，离子交换过程控制步骤取决于液膜扩散和颗粒扩散过程，可采用准数法或中断接触法来分析判断。

关键词：离子交换 动力学模型 交换机理

中图分类号：TQ0.03 文献标识码：A 文章编号：1672-3791（2015）08（a）-0021-02

膜分离是利用膜的选择透过性，在溶液两侧压力差、浓度差或电位差等推动力的作用下，分离溶液中分子、离子或某些微粒的过程。离子交换属于膜分离过程的一种，其借助于离子交换剂中的固定离子基团，与溶液中的离子发生交换，从而分离去除溶液中某些离子的过程。离子交换是一种可逆的等量交换反应，属于单元传质分离过程。

1 离子交换动力学模型

离子交换速率的快慢，可采用离子交换动力学模型来评价。按照不同的区分性质，离子交换动力学模型有多种类型。离子交换动力学模型较常见的类型有：拟均相扩散模型（包括Fick模型、Nernst-Planck模型和Maxwell-Stefan模型）、缩核模型、其他模型（大孔型动力学模型、非均相扩散模型等）。

1.1 拟均相扩散模型

Fick模型为离子交换最基本的一种模型，其假定离子在颗粒介质交换中的扩散过程符合Fick第一定律。离子扩散通量与离子浓度的梯度成正比，其扩散系数为常数。Fick离子交换动力学模型较简单，由于该模型对进行交换的离子无选择性，且要求离子扩散系数相同，从而导致Fick离子交换动力学模型在应用方面存在一定的局限性。只有在交换离子浓度微量（痕量离子）、浓度的变化值较小时，方可使用Fick模型。

Nernst-Planck模型是在Fick模型僅考虑离子在颗粒介质交换中的离子浓度梯度的基础上，同时考虑离子交换的电势梯度，也是一种较常用的离子交换动力学模型。Nernst-Planck模型未考虑同离子、活度系数、对流效应等因素对离子交换过程的影响，仍是一种简化的离子交换动力学模型。同时，由于Nernst-Planck模型近似假定离子在颗粒介质交换过程中的单独扩散系数不变（为常数），因此该模型适用范围仅限于稀溶液中的颗粒离子交换过程。

Maxwell-Stefan模型是在Nernst-Planck模型考虑离子浓度梯度和电势梯度的基础上，同时考虑了在颗粒介质交换中离子之间的相互作用力，并引入了离子相互扩散系数。其中，离子相互扩散系数与产生相互作用力的离子、固定离子基团以及离子交换的介质溶液有关。

1.2 缩核模型

缩核模型是由拟均相扩散模型发展而成的。其假定离子在颗粒介质中的交换过程刚开始在颗粒表面进行，离子交换反应随后逐步向颗粒的内部迁移，即待交换的离子通过颗粒介质反应层后，离子交换反应过程在未反应的核表面进行。离子交换反应包括颗粒表面和颗粒内部扩散过程，因此离子交换总速率是由颗粒介质反应层至未反应核的离子迁移扩散反应所决定。

1.3 其它模型

大孔型动力学模型较为复杂，在大孔介质中交换离子的扩散包括离子在微球内的扩散。大孔型动力学模型可分为并行扩散模型和连续扩散模型。其中，并行扩散模型假定交换离子在微球和大孔介质内进行并行扩散，并保持两者的平衡；而连续扩散模型假定交换离子先后依次经过微球和大孔进行连续扩散。

非均相扩散模型认为，反离子在颗粒介质中没有完全解离，而且以双电层的形式分布于孔道中。

2 离子交换机理

2.1 离子交换膜选择透过性理论

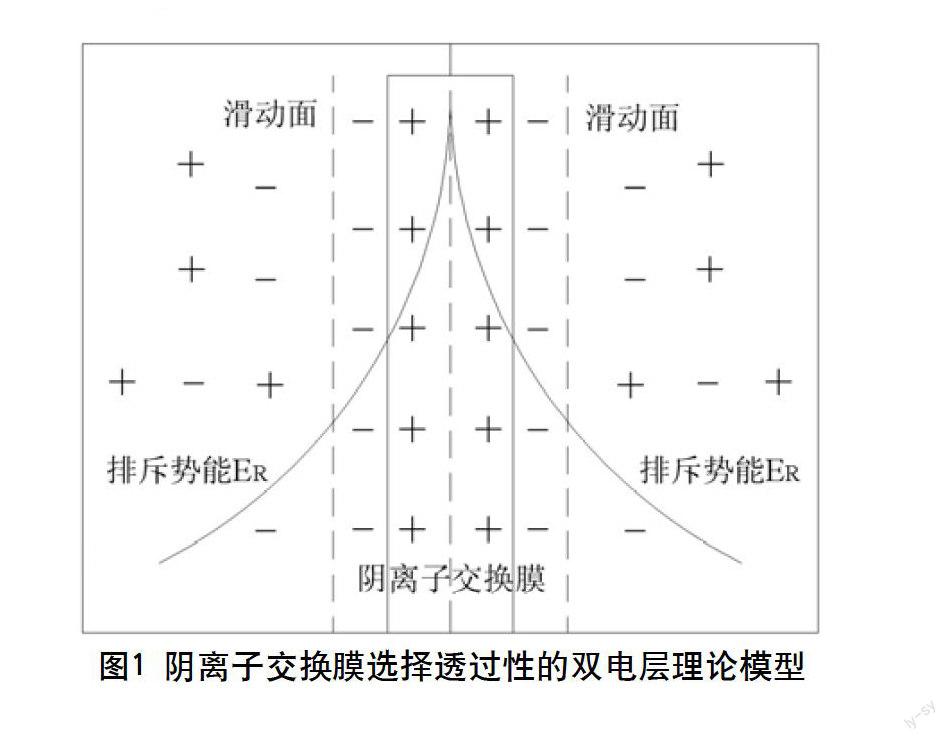
离子交换膜的选择透过性直接影响着膜对离子的分离效果和迁移交换，是离子交换膜最基本的性能之一。离子交换膜的选择透过性常采用双电层理论或Donnan膜平衡理论来解释[1]。

以阴离子交换膜为例，双电层理论认为，在溶液中发生电离后，阴离子交换膜内的固定离子基团带正电，从而在固定基团周边与溶液中带负电的离子形成双电层结构，如下图所示。此时，阴离子交换膜内的固定离子基团形成正电场，使得膜外溶液中的阳离子不能进入而阴离子容易进入膜内，这就是阴离子交换膜的选择透过性。（见图1）

Donnan膜平衡理论认为，在溶液中发生交换过程的离子和膜内离子基团会达到平衡。以阴离子交换膜为例，在达到平衡条件下，膜内的阴离子浓度大于溶液中阴离子浓度，膜内阳离子浓度小于溶液中阳离子浓度。因此，溶液中的阳离子不容易进入膜内，而阴离子则容易进入膜内，使得阴离子交换膜对离子具有选择透过性。

2.2 离子交换过程控制步骤

在溶液介质中的离子交换过程包括4个步骤，分别为对流扩散、液膜扩散、颗粒扩散和化学反应。这4个步骤中对流扩散和化学反应过程速率很快，因此离子交换过程速率控制步骤取决于液膜扩散和颗粒扩散过程，通常采用准数法或中断接触法来分析判断，并进行确定离子交换过程速率的控制步骤。

Helfferich（He）准数法可根据液膜扩散与颗粒扩散离子交换过程中半交换周期之比来确定，即离子的交换率达到一半时所需的离子交换时间之比。若He远大于1，表明液膜扩散过程的半交换周期远大于颗粒扩散过程的半交换周期，离子交换过程为液膜扩散控制；若He等于1，表明液膜扩散控制过程和颗粒扩散控制过程控制作用相同，并同时存在；若He远小于1，表明颗粒扩散过程的半交换周期远大于液膜扩散过程的半交换周期，离子交换过程为颗粒扩散控制。此外，还可以采用Biot（Bi）准数法、Vermeulen（Ve）准数法等，来分析确定离子交换过程速率的控制步骤。

准数法在一定程度上可定量分析确定离子交换过程速率的控制步骤，但是准数公式中的某些参数取值存在一定的误差和不确定性，这会影响准数计算的准确性。因此，往往可采用中断接触法，即通过试验方法测定，直观判断离子交换过程速率的控制步骤。中断接触法通过暂时中断正在进行的离子交换反应，经过一定时间后，再重新继续离子交换过程，通过测定该过程中的离子交换率与时间的变化曲线，则可分析确定离子交换过程速率的控制步骤[2]。

3 结语

拟均相扩散模型（Fick模型、Nernst-Planck模型和Maxwell-Stefan模型）、缩核模型和其他模型（大孔型动力学模型、非均相扩散模型等）各自考虑的因素及其应用范围不同。离子交换机理可通过离子交换膜选择透过性理论和离子交换过程控制步骤来分析判断。

参考文献

[1] 孟洪，彭昌盛，卢寿慈.离子交换膜的选择透过性机理[J].北京科技大学学报，2002，24（6）：656-660.

[2] 董殿权.离子交换剂的合成及交换机理研究[D].天津：天津大学，2006，92-103.