多尺度滤波器的瑞利波提取和验证

唐银国，任　波，张　健

(沈阳理工大学 装备工程学院，辽宁 沈阳 110159)



多尺度滤波器的瑞利波提取和验证

唐银国，任波，张健

(沈阳理工大学 装备工程学院，辽宁 沈阳 110159)

摘要：通过分析瑞利波的特性，提出了基于多尺度滤波器提取瑞利波的方法，主要应用于地面目标探测。在此应用背景下，通过实际的震动系统采集数据，设计出实验中需要的多尺度滤波器，分析处理并提取出瑞利波。通过其频率分布、相速度、振幅衰减规律与实际参数的对比来验证多尺度滤波器提取方法的有效性。结果与实际各项参数一致，证明此方法是可行的。

关键词：多尺度；瑞利波；提取

目前瑞利波主要用于地震勘探，在一次地震动中，包含各种波的信息，但只有瑞利波是有效波。利用瑞利波的基本特性，通过FFT变换法，将时间空间域变换为频率波数域，使用特征窗口提取出面波，消除干扰，再重构出原始时域波形[1]。本文主要把瑞利波应用在目标探测上，由于地震动信号非平稳性的特点，FFT变换不能有效地检测到地震动信号中的尖峰从而获取时间延迟，在此背景下，基于多尺度滤波器的性质，提取并验证地震动信号中的瑞利波，实验结果表明多尺度提取瑞利波的方法是可行的。

1　瑞利波的基本特性

1) 瑞利波只分布在自由界面附近并沿自由界面传播，传播时，质点在通过传播方向的铅锤面内沿着椭圆轨迹逆转运动。

2) 横波和纵波的波前相对激发点呈球面扩散，而瑞利波的波前是呈圆柱状扩散，所以其在深度方向衰减非常快，仅存在约一个波长深度内。但在沿着水平的传播方向上，其能量密度随着传播距离r按照r-1规律衰减。这比球面扩散的体波能量密度按照r-2衰减的规律要慢得多。在一次较强的地震动信号中，瑞利波的能量约占70%。

3)在均匀弹性半空间存在的瑞利波，其传播速度与横波的波速具有密切相关性，它以低于横波速度沿着自由表面传播，即纵波波速Vp、横波速度Vs和瑞利波相速度Vr满足如下关系：

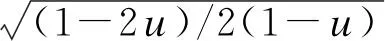
Vr/Vs=(0.87+1.12u)/(1+u)

u为泊松比，表征地下介质的软硬程度。可知，Vr约为0.92Vs，瑞利波的波速较低。

4)在一次地震动中，在时域上最先达到的直达纵波的频率约在40～120Hz；反射波和多次反射波由于其时域的特性，可以从时域区分开来，其频率范围也处于70～200Hz；干扰波的能量主要集中在高频范围内300Hz及以上。而瑞利波由于其波态特性，在公路系统中，5～40Hz频带范围内基阶波能量占主导地位；在40～70Hz频带范围内第一高阶波占主导地位；在70～100Hz频带范围内第二高阶波能量占主导地位[1]，瑞利波在所有地震动信号中频率较低。

2　瑞利波的捕获与提取方法研究

2.1　多尺度分析的基本原理

多尺度的信号分析是近年来发展起来的一种数学分析方法，是一种有效的非平稳信号的时频分析方法，其所使用的滤波器组的支撑轴可以是有限的，且能量集中在某一个带通的范围内。当尺度值a较大时，时间轴上观察范围小，而在频域上相当于用较高频率做分辨率较高的分析，即用高频做细致观察；当a值较小时，时间轴上考察范围大，而在频域上相当于用低频做概貌观。用于分析信号的频率可高可低，但在各个分析的频段内品质因素Q[即(中心频率/带宽)]却保持一致。这种性质与非平稳的地震动信号表现出的性质相吻合，其在低频分量持续时间较长，在高频分量持续时间较短[3]。

2.2　多尺度滤波器的提取原理

由于所提取的瑞利波用来获取震源的位置信息，要求滤波器具有线性相位，否则由于各个频率成分到达检波器的延迟时间不一致，很难捕获到位置信息。

图1为典型的二通道滤波器组的基本关系。

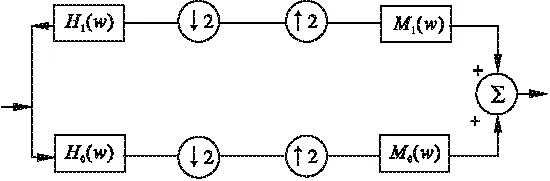
图1　二通道滤波器组的基本关系

抗混叠：H0(-z)M0(z)+H1(-z)M1(z)=0；

純延迟：H0(z)M0(z)+H1(z)M1(w)=cz-k；

式中：H1(z)、H0(z)为分解高通、低通滤波器;M1(w)、M0(z)为重构高通、低通滤波器。

抗混叠条件：1)M0(z)=+z-1H1(-z)； 2)M1(z)=-z-1H0(-z)。

可得到系统的传递函数为(令c=1,k=0,l=0)

H0(z)H1(-z)-H1(z)H0(-z)=1

则纯延迟条件为

H0(z)M0(z)+H1(z)M1(z)=1

与此相应的冲激响应关系是两支路间交叉的双正交关系：

式中：h1(n)、h0(n)为对应的冲激响应函数;m1(n)、m0(n)为对应的冲激响应函数。

和同一支路上分解和重构滤波器间的正交归一关系：

考虑到重构信号的稳定性的要求有如下公式：

若原始信号的采样率为Fs，通过H0(w)和M0(w)滤波器系数的多尺度的分解和重构，在尺度值为n时，(n,k)节点所在的通带范围为(Fs·k/2n,Fs·(k+1)/2n)。

由于地质情况的差异性和随机性，以及仪器本身所带来的影响，都不可避免地有噪声干扰，但是地震动信号本身具有非平稳的特性，突发性较强。多尺度阈值滤波法是在非线性小波阈值滤波法基础上的一种改进，会在多个尺度下选择不同的滤波阈值对信号进行滤波。由于多尺度滤波器的品质因素在各个尺度下保持一致，可以有效地克服低尺度上会去除部分有用信号和高尺度上会保留部分噪声的缺点。

在多尺度分解滤波器对信号进行分解后，在每一个尺度下都采用不同的阈值进行滤波，然后再对信号所在频率段的节点进行重构，即可得到所需要的信号。

通过分析瑞利波的振幅衰减规律、瑞利波的相速度、及其所在的频率范围，并与实际参数对比，可以验证瑞利波提取的有效性。

2.3　多尺度滤波器的参数设计

图2　滤波器参数

3　数据分析与处理

3.1　数据采集

实验器材和实验场地参数如下：

实验场地为市郊某城际公路，长度为500m，桩号为220～230；采集卡的型号为nextkitS，最高采样率为51.2KS/s，动态范围为102dB；传感器的型号为泛华的垂直方向加速度震动传感器；放大器型号为YE3821，放大倍数为X10；使用20g左右的炸药作为震源；采样频率Fs为25600Hz；记录长度为20s。上位机：华硕A43S型号笔记本，CPU为i5core，内存为8G，数据采集及处理所使用的软件为Labview2012，界面如图3所示。

图3　Labview2012界面图

观测系统的示意图如图4所示：震动传感器距离爆炸点的距离分别为50m、75m、100m、125m、150m、200m、250m、300m、350m、400m。

3.2　数据处理

3.2.1　原始数据波形图

图5a～d分别是50m、75m、100m、125m处的原始数据波形。

图4　震动系统观测示意图

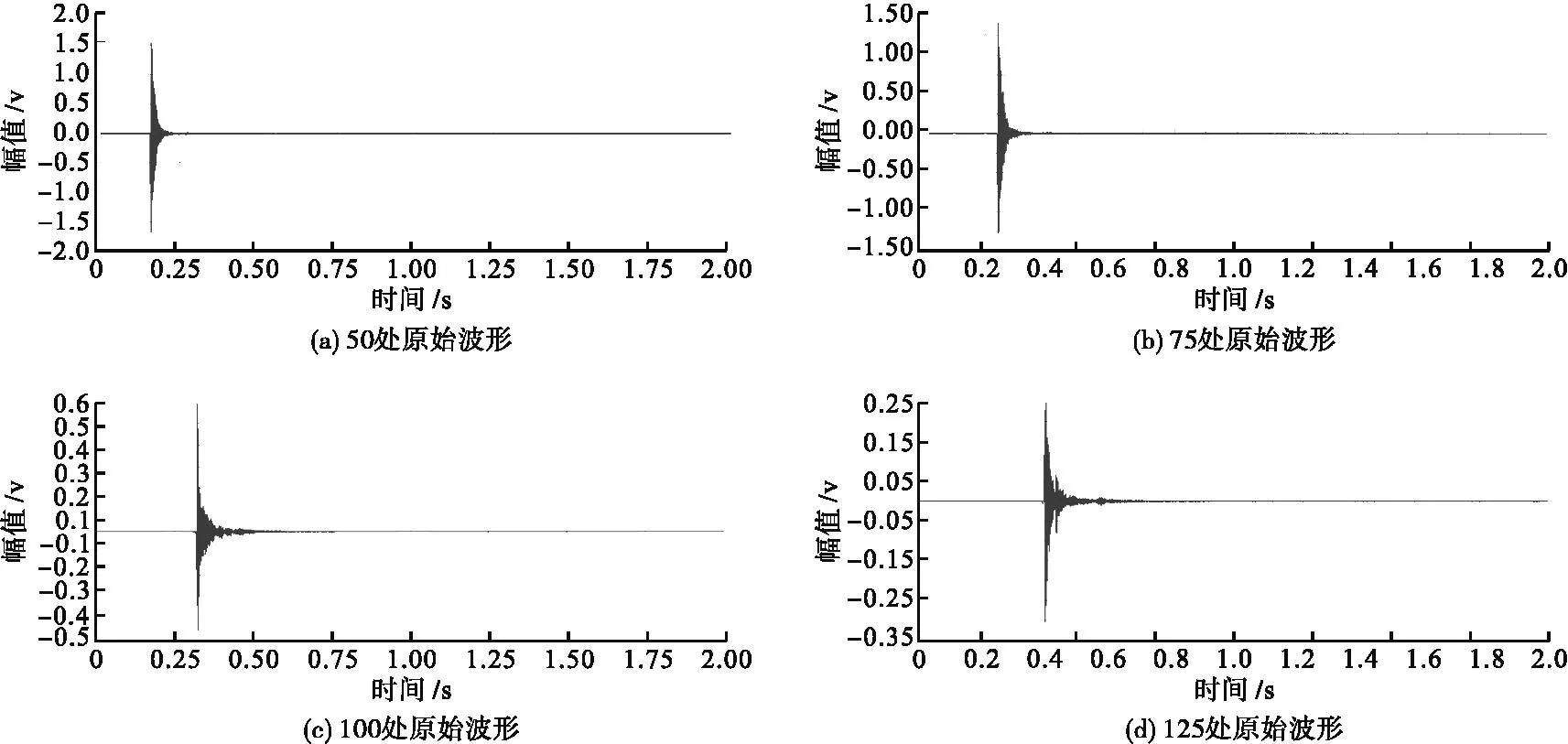
图5　各处对应的原始波

3.2.2　去除零点漂移

由于传感器本身的器件特性，野外工作的时候，采集进来的数据明显存在基线和斜率零点漂移的现象。为了获得更好的时域波形，以及时间所对应的幅值关系，对每个通道采集到的数据做了处理，用来消除漂移所带来的影响，图6a是在125m处震动传感器所观测到的零点漂移现象，图6b是使用去除漂移之后的效果。

3.2.3　多尺度滤波

图8为50m处经过多尺度去噪滤波后的波形，其中W1为初至波，W2和W3为反射波和多次反射波，也可能是通过底层介质传播过来的折射波，W1、W2、W3由于其传播特性和时域特性很容易从波形图中辨别出来，W4为瑞利波[5-7]。

图6　去除零点漂移的对比

图7　去噪信号的对比

图8　50m处去噪滤波后的波形

3.2.4　信号的重构及其与FIR数字器滤波的对比

图9a为100m处去噪滤波后采用(7,0)节点重构的波形图，重叠部分的波形凸显出来，可以观察到W所指波形有一层包络，文献显示瑞利波有以包络形式衰减的特征，下面通过验证W处所指向的波形的各种特征[8]，可知该处即为瑞利波。

图9　尺度滤波器和FIR滤波器滤波后的对比

图9b为100m处原始信号经过order数为200的FIR线性数字滤波器。窗口指定为bartlett-Hanning窗，截止频率为100Hz，阻带衰减为6dB。可以很明显地观察到，虽然振幅与多尺度滤波器信号重构之后的波形在同一量级，但是信号更加平滑，从时间域已经不能辨别出信号W处所指向的包络，对于需要用地震动信号中瑞利波与直达波的时间延迟来计算距离的作用小。

3.3　瑞利波的验证

在地形参数、传感器布置和爆破点距离已知的情况下，计算出W处所指向的瑞利波的频率范围、相速度、振幅衰减规律，通过与实际参数的对比，验证瑞利波提取的有效性。

3.3.1　瑞利波的频率分析及验证

图10a、b、c分别为50m、75m、100m处经过滤波去噪，并且重构后W处所指向瑞利波的功率谱。可以发现其所处的频率范围为20～60Hz，功率谱幅值逐渐减小，符合实际情况。并且在100m处80Hz～120Hz波段出现二次波峰，这是由于发生了某种程度的频散现象，各频率段与瑞利波基本特性分析中所说明的频率段一致。

图10　多尺度滤波器提取出的波形W处瑞利波的功率谱

3.3.2　瑞利波的相速度分析及验证

已测本地形初至波速度约为330m/s±15m/s，在已知初至波的波速情况下，推算出50m处W所指向的瑞利波的峰值处波速约为124m/s。表1为尺度滤波器去噪滤波并使用(7，0)节点重构之后各处瑞利波对应的峰峰值和相速度。

表1　尺度滤波器(7，0)节点滤波后所对应的峰峰值和相速度　m/s

3.3.3　瑞利波振幅衰减的分析及验证

图11　拟合出的幅值和距离对应的关系

4　结论

在各项参数已知的情况下，分析信号中各种震动信号的时域特性，利用尺度滤波器组提取出地震动信号中的瑞利波。通过验证其所在的频率段、相速度以及振幅衰减规律与实际参数的对比，说明此研究方法可以有效地提取出瑞利波。若震源未知，地形参数已知的情况下，可以确定瑞利波

的频率成分以及初至波的速度，通过多尺度滤波器处理之后所得到的瑞利波，分析其与初至波到达传感器的时延差可以确定震源的位置。另外分析其振幅衰减，可以得到震源处所产生瑞利波的振幅以确定震源处振动的量级，需要进一步实验研究分析。

参考文献：

[1]单娜琳,程志平,刘云祯.工程地震勘探[M].北京：冶金工业版社，2006:122，126-127.

[2]宋先海,李瑞有,顾汉明.瑞利波勘探理论及其应用[M].北京：中国水利水电出版社,2010：2,38,54.

[3]杨福生.小波变换的工程分析与应用[M].北京：科学出版社,2000:3-4,102-104.

[4]张德丰.MATLAB小波分析[M].北京：机械工业出版社,2012:223-224.

[5]李响,颜冰,周穂华.基于直达波与地声界面波时延的目标定位方法[J].探测与制导学报，2012,32(6):51-52.

[6]刘强.基于瑞雷波理论的公路无损检测方法研究[D].西安：长安大学，2009:14-16.

[7]熊章强,周竹生,张大洲.地震勘探[M].长沙：中南大学出版社，2010：39-40.

[8]Szendrei ME.The frequency content and attenuation of seismic wavelets along the surface of different types of soil[J].Pure and Applied Geophysics，1960,46(1):47-48.

(责任编辑：马金发)

Extraction and Validation of Rayleigh Waves Based on Multi-scale Filter

TANG Yinguo,REN Bo,ZHANG Jian

(Shenyang Ligong University,Shenyang 110159,China)

Abstract：Raleigh wave characteristics are analyzed and extracted based on multi-scale filter,which is mainly applied to the detection of ground targets.Data is collected by actual vibration system and the multi-scale filter is designed,which is required in the experinent.Finally，the Raleigh wave is extracted to process and analyze，which verifies the feasibility of method to multiscale extraction filter by comparing the frequency distribution,the phase velocity and the amplitude attenuation law.Simulation results are consistent with actual parameters,which show that the proposed method is feasible.

Key words：multi-scale;Rayleigh wave;extraction

中图分类号：TP391

文献标志码：A

文章编号：1003-1251(2015)01-0040-06

通讯作者：

作者简介：唐银国(1989—)，男，硕士研究生；任波(1962—)，男，教授，研究方向：信号处理、导航制导等.

收稿日期：2014-03-04