二维离散系统的H∞滤波仿真研究

姜　静，董丽鑫

(沈阳理工大学 信息科学与工程学院，辽宁 沈阳 110159)



二维离散系统的H∞滤波仿真研究

姜静，董丽鑫

(沈阳理工大学 信息科学与工程学院，辽宁 沈阳 110159)

摘要：基于Roesser模型对二维离散系统的H∞滤波问题进行研究，讨论了二维H∞滤波器的设计方法。针对任意能量范围内的噪声输入，二维H∞滤波器能保证噪声衰减的水平。应用LMI(线性矩阵不等式)方法和黎卡提不等式方法处理二维H∞滤波问题。设计基于观测器的H∞滤波器，最后通过图像处理的相关实例进行结果仿真验证。仿真结果表明，滤波误差系统的频率响应低于指定的H∞噪音衰减水平，滤波效果明显。

关键词：二维离散系统；Roesser模型；H∞滤波器；线性矩阵不等式；黎卡提不等式

工程上常用的滤波算法是Kalman滤波算法，但是Kalman滤波器计算较为复杂，并且它要求精确已知系统的数学模型和噪声统计，当这些条件不能很好满足时，Kalman滤波的性能将遭到破坏。随着鲁棒控制理论的发展，提出了H∞优化设计的鲁棒滤波技术，其设计思想是使得噪声能量和估计误差能量的最大比值小于某一正数，从而确保在任意有限能量干扰下所得到的估计误差能量最小[1]。二维有界实引理可以应用LMI[2]和Riccati不等式解决二维H∞滤波问题[3]。本文主要完成基于观测器的H∞滤波器设计。

1　二维离散系统模型

各种线性离散二维状态空间模型中，Roesser模型是最常见的也是最有用的模型之一，它在图像处理等领域有十分重要的应用。

Roesser模型为

(1)

(2)

(3)

式中：xh∈Rn1、xv∈Rn2分别是横向状态，纵向状态；ω∈Rq是属于l2{(0，∞)，(0，∞)}的噪音信号；y∈Rl是测量输出；z∈Rp是待估信号；A、B、C、D和L为适当维数的常值实数阵。

2　二维系统有界实引理

线性系统的一个基本属性是有界实性，它与线性系统的稳定性和有限增益(即H∞范数)有关。在状态空间设置中的一维 H∞控制和滤波问题的解决方案很大程度上依赖于所谓的有界实引理，它涉及到系统的有界实性质。

根据一维系统的H∞噪音衰减的概念，定义二维系统的H∞噪音衰减如下：

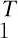
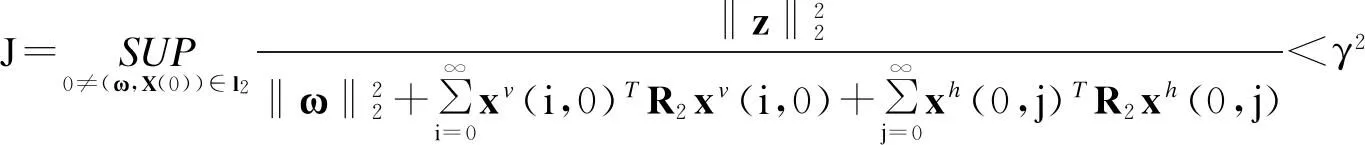
(4)

则称二维系统式(1)～(3)有H∞噪音衰减γ。

当已知边界条件为0时，即X(0)=0，式(4)可以写成

(5)

考虑二维Roesser模型：

(6)

(7)

定理1给定一个正标量γ，如果满足下面任意的等价条件，则称未知边界条件二维系统式(6)～(7)有H∞噪音衰减γ。

(1)如果存在块对角矩阵P=diag{Ph,Pv}>0，其中Ph∈Rn1×n1，Pv∈Rn2×n2满足Ph<γ2R1和Pv<γ2R2,则使得

ATPA-P+γ-2(ATPB+HTL)[I-γ-2(BTPB+LTL)]-1(BTPA+LTH)+HTH<0

(8)

并且I-γ-2(BTPB+LTL)>0。

(2)存在一个针对LMI块对角矩阵，

Y=diag{Yh,Yv}>0,

(9)

3　基于观测器的H∞滤波器设计

应用定理1设计基于观测器的H∞滤波器。

3.1　基于观测器的H∞滤波器形式

根据二维状态观测器理论，基于观测器的二维滤波器形式适用于系统(1)～(3)研究二维H∞滤波问题：

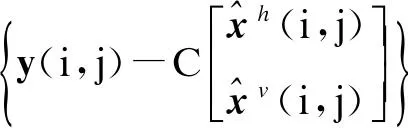
(10)

(11)

记状态估计误差为

(12)

从式(1)～(3)和式(10)～(12)，可以得到误差系统：

(B-KD)ω(i,j)

(13)

(14)

这样就找到了如同式(10)形式的滤波器，使其误差系统渐进稳定，并且满足式(4)。

3.2　黎卡提不等式方法

假定DDT>0，即所有的测量受噪声干扰。

定理2为系统(1)～(3)提供一个黎卡提不等式方法实现H∞滤波。

对于ARI

(15)

在这种状况下，可以得到一种合适的滤波增益：

K=(AVCT+LTDT)(CVCT+DDT)-1

(16)

式中，V=Q+γ-2QBΩ-1BTQ。

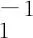
(A-KC)TQ(A-KC)-Q+γ-2(A-KC)TQB

(I-γ-2BTQB)-1BTQ(A-KC)+LTL<0

(17)

公式(17)重新给定如下条件

ATQA-Q+LTL+γ-2ATQBΩ-1BTQA

+K(DDT+CQCT+γ-2CQBΩ-1BTQCT)KT

-K(CQA+DL+γ-2CQBΩ-1BTQA)

-(ATQCT+LTDT+γ-2ATQBΩ-1BTQCT)KT<0

(18)

并且，令LA=γ-1BTQA，CA=COA+DL,LC=γ-1BTQCT,

(19)

根据定理2中的假设DDT>0，X1>0，可以得到

(20)

因此，在公式(15)和(18)中的Q和K满足不等式(17)，可以实现H∞滤波。

3.3　LMI方法

文中应用LMI方法来计算滤波器得到式(10)中的K。

定理3针对未知边界条件时考虑二维系统(1)～(3)，给定噪音衰减γ>0，且常数加权矩阵R1>0,R2>0如果存在一个实对称矩阵P=diag{Ph,Pv}>0，其中Ph∈Rn1×n1,Pv∈Rn2×n2满足Ph<γ2R1和Pv<γ2R2且有秩为(n1+n2)×l的矩阵S，则存在一个形式为式(10)的滤波器来解决二维 H∞滤波问题[6-10]。

对于LMI满足

(21)

这里，通过K=P-1S对式(10)给出一个合适的滤波器。

证明考虑滤波器的误差系统(11)～(12)。由定理1(2)，如果存在一个实对称矩阵P=diag{Ph,Pv}>0，满足Ph<γ2R1，Pv<γ2R2则系统有H∞噪音衰减γ，所以

(22)

当S=PK时，式(21)成立，所以可得K=P-1S。

4　实例验证

文中设计一个图像处理中固定随机场的二维 H∞滤波器。通常，平稳随机场可以用如下二维系统模型表示：

η(i+1,j+1)=a1η(i,j+1)+a2η(i+1,j)

-a1a2η(i,j)+v1(i,j)i=0,1,…,j=0,1,…

(23)

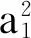
记xh(i,j)=η(i,j+1)-a2η(i,j)，并且xv(i,j)=η(i,j)。方程(23)可以转换成形式为式(1)的二维Roesser模型：

令a1=0.2,a2=0.1，假定测量输出和待估信号如同式(2)、(3)所示。

C=[01]，D=1，L=[01]

并且，系统是零边界条件。

首先，应用定理2黎卡提方法设计H∞滤波器，通过计算机仿真，噪音衰减的最优标准是γ=1.16。

其中，滤波器的增益为

其次，考虑一个基于观测器的二维滤波器(10)～(11)，并且用定理3来为随机场系统(23)设计一个H∞滤波器。通过计算机仿真，得到噪音衰减的最优标准是γ=1.16。

根据式(21)给出相一致的解决方法为

得到滤波器的增益为

扰动ω到估计误差系统的传递函数为

G(z1,z2)=L[diag{z1In1,z2In2}-(A-KC)]-1(B-KD)

滤波前系统的频率响应图如图1所示。

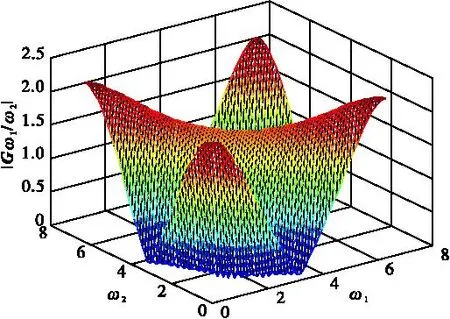
图1　滤波前系统的频率响应图

在Matlab仿真环境下，|G(ejω1,ejω2)|，令0<ω1<2π，0<ω2<2π，滤波误差的频率响应如图2所示。

图2　滤波误差的频率响应图

可以看出滤波误差系统的频率响应低于指定的H∞噪音衰减水平γ=1.16，滤波效果明显。

5　结论

讨论了设计基于观测器的二维H∞滤波器的中的黎卡提不等式和LMI方法，给出了用Roesser模型描述的二维系统的H∞滤波器的设计过程。针对一个图像处理中的实例进行了计算机仿真，验证了LMI方法的滤波效果。采用Roesser模型解决二维离散系统H∞滤波问题的LMI方法不同于黎卡提方法，LMI方法的优点是它的计算功能。

参考文献：

[1]ChunlingDu,LihuaXie,CishenZhang.H∞control and robust stabilization of two-dimensional systems in Roesser models[J].Automatica,2001,37(2):205-211.

[2]俞立.鲁棒控制—线性矩阵不等式处理方法[M].北京:清华大学出版社,2002.

[3]王瑜.基于LMI方法的2-D鲁棒H2/H∞滤波器的设计与研究[D].长春:吉林大学,2007.

[4]郝鹏,刘维亭.基于Riccati法和LMI法的系统鲁棒控制器比较研究[J].电气传动自动化，2004,26(4):8-9.

[5]张明,施鼎汉.代数Riccati不等式与H∞滤波器[J].厦门大学学报,1997,36(6):825-828.

[6]ChunYanGao,GuangRenDuan,XianYuMeng.RobustH∞Filter Design for 2-D Diserete Systems in Roesser Model[J].International journal of automation and computing,2008,5(4):413-418.

[7]AmitDhawan,HaranathKar.AnLMIapproachtorobustoptimalguaranteedcostcontrolof2-DdiscretesystemsdescribedbytheRoessermodel[J].Signalprocessing,2010,90(9):2648-2654.

[8]XianweiLia,HuijunGao.RobustfinitefrequencyH∞filtering for uncertain 2-D Roesser systems[J].Automatica,2012,48(6):1163-1170.

[9]MaoWeihua,DengFeiqi,WanAnhua.RobustmixedH2/H∞filtering for uncertain stochastic systemswith interval time-varying delays[C].Proceedings of the 31st Chinese Control Conference,2012:1676-1683.

[10]AmitDhawan,HaranathKar.AnimprovedLMI-basedcriterionforthedesignofoptimalguaranteedcostcontrollerfor2-Ddiscreteuncertainsystems[J].SignalProcessing,2011,91(4):1032-1035.

(责任编辑：马金发)

H∞Filtering Simulation Based on 2-D Discrete Systems

JIANG Jing，DONG Lixin

(Shenyang Ligong University,Shenyang 110159,China)

Abstract：H∞filtering problem of 2-D discrete state systems is investigated by Roesser model，and a linear 2-D filter is designed.2-D filter guarantees a prescribed level of H∞noise attenuation for any energy bounded noise input.The 2-D H∞filtering problem is solved by Riccati inequality and LMI approach.Observer-based 2-D H∞filter is designed,which verifies the related examples image through simulation results.The simulation result shows that the filtering error system frequency response is below the level of H∞noise attenuation and filtering effect is obvious.

Key words：2-D Discrete State system;Roesser model;H∞filter;LMI;riccati inequality

中图分类号：TP29

文献标志码：A

文章编号：1003-1251(2015)01-0029-05

作者简介：姜静(1973—)，女，副教授，博士，研究方向：复杂系统的建模、优化、控制及仿真。

收稿日期：2014-04-11