基于灰色残差马尔可夫模型的郑州市旱涝灾害预测
2015-12-11罗党林培源李钰雯
罗党,林培源,李钰雯
(华北水利水电大学,河南 郑州 450045)
我国农业的综合抗灾能力不强,每年的旱涝灾害都会给我国农业造成不小的损失. 郑州市位于华北平原中部,属北温带大陆性季风气候,旱涝灾害较为频繁,特大旱灾时有发生,这给生态环境和人民财产造成了无可挽回的重大损失.因此,合理预测郑州市旱涝灾害的发生,做好防范措施,对保障人民的生命财产安全有着重要的现实意义.
灰色系统理论中的GM(1,1)模型主要用于某一主导特征因素的拟合和预测,从而揭示其变化规律及未来发展态势[1].针对GM(1,1)模型在对非光滑序列数据的处理和预测中拟合较差的问题,DGM(1,1)模型从由离散直接到离散的角度解决了预测不稳定的问题,然而DGM(1,1)模型对随机波动大的数据仍然存在预测精度较低的问题[2-3]. 本文采用马尔可夫模型来弥补DGM(1,1)模型的局限,并选取郑州市1955—2014 年的降水量数据,建立干旱和雨涝的灾变日期序列,运用灰色残差马尔可夫预测模型对郑州市旱涝灾害进行趋势预测.
1 灰色残差马尔可夫预测模型
1.1 建模机理
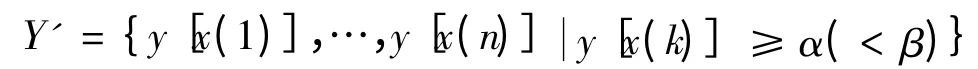
非负序列X(0)经一次累加,生成序列为
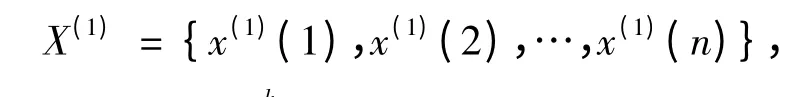

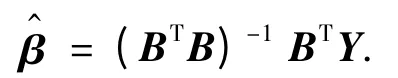
取x(1)(1)= x(0)(1),则递推函数为

因还原值为

得时间响应式为

式中k = 1,2,…,n -1.
由于模型(3)只适用于序列为非负的数据列,故可对残差序列的绝对值建立DGM(1,1)模型. 应用马尔可夫模型判断残差预测值在k >n 时的符号,以提高预测精度.

将式(4)与式(3)合并,建立灰色残差模型:
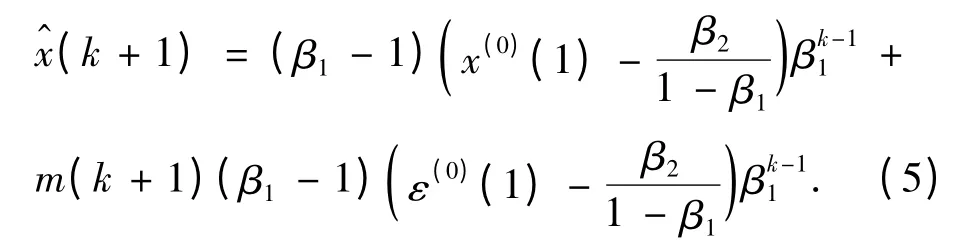
其中
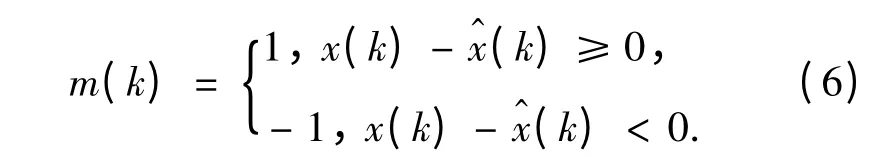
由此可见,提高灰色预测精度的关键是准确预测k >n 时m(k)的值.为了准确预测m(k),这里引入马尔可夫模型.
马尔可夫模型是一种研究事物的状态及其转移的统计分析方法.其特点是无后效性,即系统当前所处状态只与之前所处状态有关,与之后状态无关[4-6].对DGM(1,1)残差的符号序列建立马尔可夫模型,其步骤如下:
1)确定状态.残差为正时状态记为+1(E1),残差为负时状态记为-1(E2).
2)根据残差状态求出状态转移矩阵P(m).

其中pij(m)= Mij/Mi;i,j = 1,2;Mij(m)为由状态Ei经过m 步转移到状态Ej的原始数据的个数;Mi为处于状态Ei时原始数据的个数.
3)确定初始状态向量π(0).
4)根据状态转移公式π(0)π(t)= π(0)Pt,求出第t 期状态转移的结果,取概率大的状态.如果正负号概率相等,取上期确定的符号[7-8].
1.2 建模步骤
步骤1 运用均值- 标准差旱涝等级划分法对降水量划分等级.
步骤2 取定灾变点,分别建立干旱和雨涝灾变日期序列.
步骤3 通过式(3)对干旱和雨涝灾变日期序列建立DGM(1,1)模型.
步骤4 计算平均相对误差.
步骤5 建立残差绝对值的DGM(1,1)模型.
步骤6 通过式(7)对残差符号建立马尔可夫状态转移矩阵.
采用SPSS 20.0统计学软件进行数据分析,计量资料用(±s)表示,采用 t检验,计数资料用[n(%)]表示,采用χ2检验,P<0.05为差异有统计学意义。
步骤7 结合DGM(1,1)模型与马尔可夫状态转移矩阵结果得到最终预测值.
2 实例分析
郑州是我国农业大省河南省的省会城市,旱涝灾害不仅是影响其粮食生产的主要因素,而且还会引发其他自然灾害.因而预测灾害发生,防患于未然尤为重要.依据郑州市1955—2014 年年降水量数据(来源于河南省统计年鉴),建立模型预测2014 年之后的干旱和雨涝灾害发生年份.步骤如下:
步骤1 根据郑州市60 a 年降水量数据,计算得年降水量序列均值x-= 640.19 mm,标准差s =158.17 mm.取α1= 1.1,α2= 0.5,运用均值-标准差旱涝等级划分法[5-6],将郑州市降水量划分为干旱、偏旱、正常、偏涝和雨涝5 个状态,见表1.

表1 降水量的分级标准mm
依据郑州市1955—2014 年年降水量数据和干旱、雨涝的降水量临界值绘制降水量图,如图1 所示.
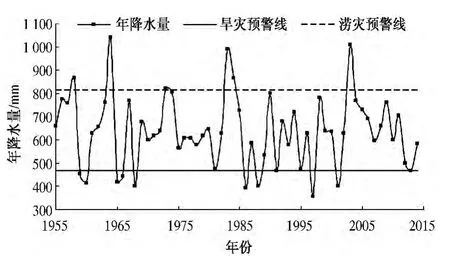
图1 郑州市1955—2014 年年降水量变化图
由于干旱和雨涝均是自然现象中的非常态,准确预测干旱和雨涝发生的时间具有重要的实际意义.郑州市1955—2014 年年降水量异常状态汇总见表2.
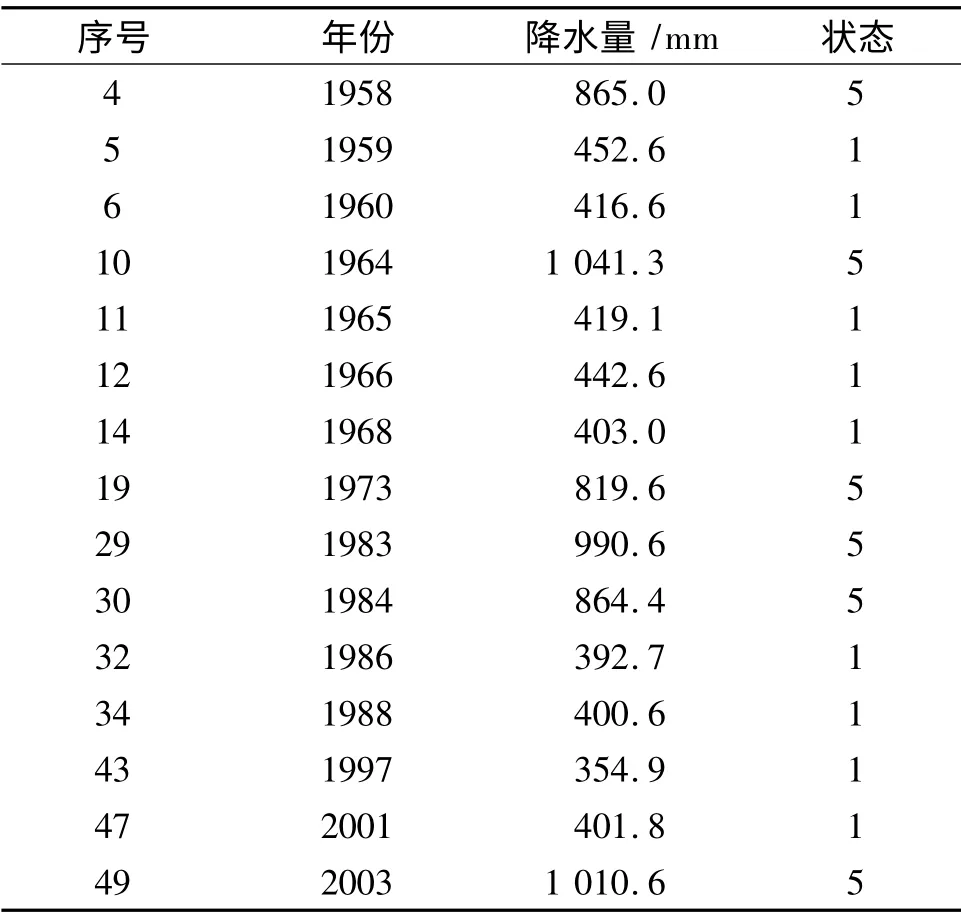
表2 1955—2014 年年降水量异常状态汇总
步骤2 状态1 的灾变日期序列为

状态5 的灾变日期序列为
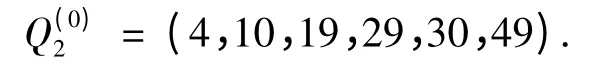
步骤3 对干旱和雨涝灾变日期序列建立DGM(1,1)模型,求解可得到干旱和雨涝灾变日期序列的DGM(1,1)模型的时间响应式.
干旱:
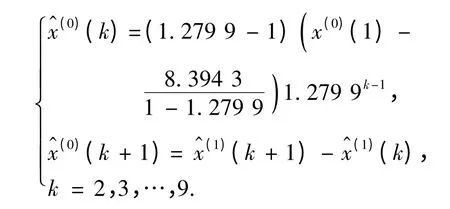
雨涝:

对应的平均相对误差分别为

步骤4 依据干旱和雨涝灾变日期序列的时间响应式,分别计算得灾变日期序列的残差序列,见表3.分别对残差绝对值序列建立DGM(1,1)模型,对应的时间响应式分别为
干旱:
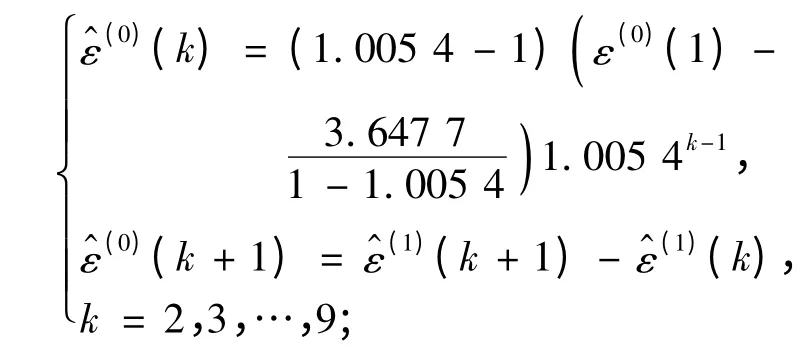
雨涝:
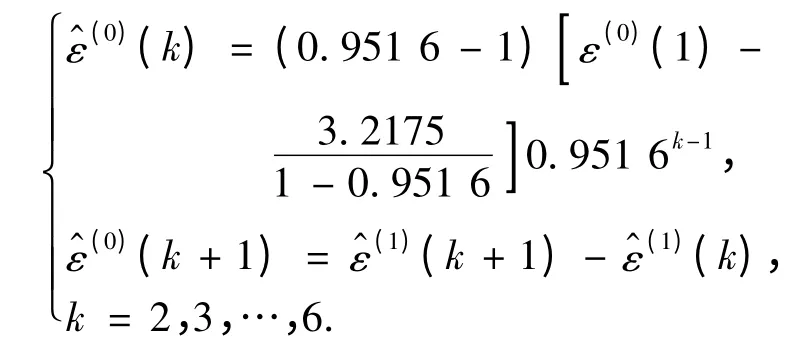
对应的平均相对误差为:

干旱和雨涝灾变日期序列的计算结果见表3.

表3 干旱和雨涝灾变日期序列的计算结果

续表
步骤5 以干旱灾变日期序列为例,确定其残差符号.类似地,可预测雨涝灾变日期序列的残差符号.
建立马尔可夫模型预测m(k +1)在k =9 时的值,即预测第10 次干旱灾变日期序列的残差符号.由表2 计算可得马尔可夫转移概率矩阵:

解得m(10)= +1.
步骤6 类似地,可得到干旱和雨涝灾变日期序列的向后两步预测值,见表4.

表4 干旱和雨涝灾变日期序列的向后两步预测
干旱和雨涝灾变日期序列的原始值与预测值拟合情况分别如图2 和图3 所示.
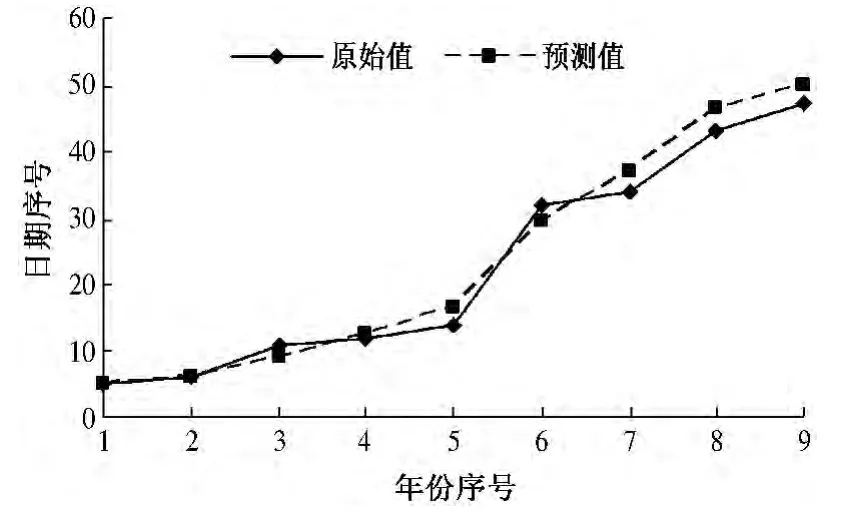
图2 干旱灾变日期序列原始值与预测值拟合

图3 雨涝灾变日期序列原始值与预测值拟合
由表4 可知,2018 年和2038 年前后会发生严重旱灾,2022 年和2048 年前后会发生严重涝灾,应提前做好防范措施.由图2 和图3 可知,对干旱和雨涝的拟合精度均较好.
3 结 语
灰色残差马尔可夫模型兼具DGM(1,1)模型与马尔可夫模型的优点,增强了模型的适应性,提高了预测精度,是一种方便、可靠的预测方法.
该模型对旱涝灾害的预测结果可以为研究郑州地区今后的旱涝灾害等级提供理论依据,从而有效地指导今后的防灾减灾工作,对郑州市目前储水量的开发、利用、配置、保护等方面也具有实用价值.
[1]刘思峰,杨英杰,吴利丰,等. 灰色系统理论及其应用[M].北京:科学出版社,2014:140 -151.
[2]连世伟,薛磊,王宪栋,等. 基于残差递推的自适应GM(1,1)模型[J]. 系统工程与电子技术,2013,35(10):2141 -2144.
[3]钱吴永,党耀国.基于振荡序列的GM(1,1)模型[J].系统工程理论与实践,2009,29(3):149 -154.
[4]Xiao X P,Guo H,Mao S H.The modeling mechanism,extension and optimization of grey GM(1,1)model[J].Applied Mathematical Modelling,2014,38(s5):1896 -1910.
[5]何一鸣,蒲英霞,王结臣,等.基于马尔可夫链的四川省产业结构时空演变[J].中国人口·资源与环境,2011,21(4):68 -75.
[6]彭世彰,魏征,窦超银,等.加权马尔可夫模型在区域干旱指标预测中的应用[J].系统工程理论与实践,2009,29(9):173 -178.
[7]赵玲萍,王俊,张凤娥,等.基于灰色残差马尔可夫藕合模型的农业需水量预测研究[J].节水灌溉,2010(11):4 -6.
[8]邱林,安可君,王文川,等.基于Bayes 分类的Markov 径流量预测模型[J]. 水利科技与经济,2011,17(12):1 -4.
