数学期望几个公式的证明
2015-12-11朱诗红
朱诗红
(铜陵学院,安徽 铜陵 244000)
数学期望几个公式的证明
朱诗红
(铜陵学院,安徽 铜陵 244000)
《概率统计》教学中,在讲授数学期望这一节时,许多学生认为连续型随机变量或连续型随机向量的几个计算公式给出比较突然,不易理解.因此在已知离散型随机变量数学期望的计算公式的前提下,利用微积分的极限思想,说明了这几个公式是如何成立的。不仅有助于学生理解掌握这几个公式,而且使学生领略极限在解决问题时的妙用。
数学期望;随机变量;极限;连续型
在国内,许多本科院校学生使用的《概率论与数理统计》教材中,离散型随机变量的数学期望往往是通过计算通常意义下平均数引入,然后再从随机变量角度考察这个平均数并且推广而得出离散型随机变量的数学期望的定义。而连续性随机变量的数学期望的计算公式几乎都是在介绍离散型随机变量的数学期望之后直接给出,因此很多同学都难以接受。“为什么是这种形式?”“怎么得到的这个公式的?”学生们这样的疑问不绝于耳。老师往往由于课时的限制,只能解释说“这个公式只要会运用即可,特别是对于我们经管类的学生”。尽管有些好奇心特别强的同学下课时和我们一起探讨了这个问题,而大多数同学由于种种原因搁置了这个问题或者“心甘情愿”地接受它们。所以,想借助此文以消除这些同学对这些问题的困惑。
一、随机变量的数学期望
先看随机变量数学期望的定义



对于(1)式,大多数老师在讲授时都是用一个求平均值得实例引入,然后将这个实例一般化推广而得到.而对于(2)时却不作说明地直接给出.这给许多同学造成疑惑,甚至囫囵吞枣.
实际上,我们可以按如下几步得到公式(2):

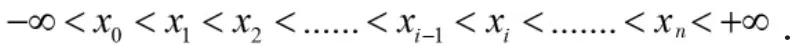
且相邻的两点相差一个很小的常数,即这些点将x轴划分成无数个小区间.

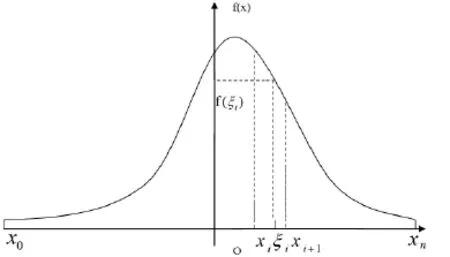
图1 区间△xi曲边梯形图
区间△xi所对应的曲边梯形如图所示.



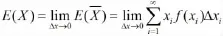
再由定积分的定义可得:
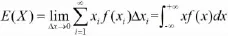
二、连续型随机变量函数Y=g(X)的数学期望

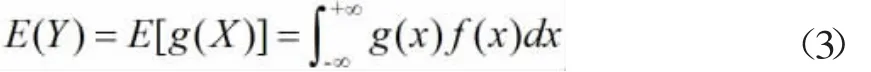
下面给予简单的证明。
证明:
1.同上(略)。
2.同上(略)。
3.近似.考虑最简单的情形:

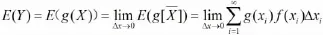
再由定积分的定义可得:

若Y=g(X)不是单调连续的,则需分段考虑,也可得到相同的结论。
三、连续型随机向量函数的数学期望



图2 △Vi曲顶柱状图
下面给予简单的说明.

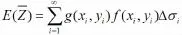
O212
C
1672-0547(2015)05-0105-02
2015-09-18
朱诗红(1972-),男,安徽芜湖人,铜陵学院数学与计算机学院教师,研究方向:调和分析。
