Matlab平台下遥感影像的北方岸线提取研究——以大连长兴岛为例<br/>

Matlab平台下遥感影像的北方岸线提取研究——以大连长兴岛为例

2015-12-11魏东岚曹晓晨

测绘通报 2015年5期

魏东岚，曹晓晨

(辽宁师范大学城市与环境学院，辽宁大连116029)

一、引言

海岸带处于海洋与陆地交界处，其自然资源丰富，地理位置优越，是人类竞争和开发海洋的重要区域。海岸线作为海陆分界线，是研究海岸带动态变化最重要的标准之一。同时，海岸线也是沿海滩涂面积、湿地生态系统衰退与否的重要标志，其变迁反映了全球环境变化、海岸环境变化及人类活动相互作用的结果。因此，对海岸线地理位置确定的研究具有十分重要的意义。

近年来，随着卫星遥感技术的发展，海岸线提取技术逐渐向多时空多元化的方向发展。遥感技术具有多时空多尺度多平台等特点，数据来源广，覆盖面积大，可以对研究区域进行宏观、详细的检测，得到的海岸线信息更加精确，时效性更强。因此，利用卫星遥感图像进行海岸线提取逐渐成为获取海岸线数据的主要手段。

目前通过遥感数据对海岸线进行提取的方式主要分为两大类:目视解译和自动解译［1］。传统的目视解译仅仅利用GIS软件对遥感原始图像进行手工矢量化。该方法操作简单，但工作量大，准确性差。随着GIS与遥感技术及图像处理软件的逐步发展，自动解译逐渐代替传统的目视解译。自动解译是对原始遥感图像进行数据分析处理，使用自动或半自动的方式将海岸线作为图像中的特征地物提取出来，该方法的核心是对原始遥感图像的处理与分析。自动解译的优势在于其提高了准确性的同时，具有较高的效率。目前使用较多的自动解译方式主要有阈值分割法、边缘提取法、小波变换法等。

近年来，国内外研究人员从各个方面对海岸线提取方法进行了逐步的完善。国外方面，Andreas Niedermeie将区域跟踪法、小波变化法及海岸线的Snake算法3种方法进行综合使用，实现了对水线的提取。国内方面，陈明泉等利用Matlab采用局部阈值法对海岸线进行的提取，验证了Matlab在海岸线提取中具有方便、易用的优点［2］;崔步礼、常学礼等在对黄河口海岸线动态监测时，使用了阈值分割法对海岸线进行了提取［3］;庄翠蓉等根据不同海岸类型的地貌特点，综合Robert算子、Sobel算子和小波多尺度边缘检测等提取解译方法，对厦门地区海岸线的变迁进行了研究［4］;李秀梅等在对渤海湾海岸带遥感监测及时空变化时，使用Canny算子对海岸带进行了提取［5］;马小峰、赵冬至等应用Canny算子、中值滤波和腐蚀算子对大连营口海岸带进行了位置的校正［6］;郭衍游、卢霞、邵飞卿等利用小波变换法对连云港海岸线进行提取，通过GPS对海岸线实地观测，验证了小波变换对遥感图像的增强效果明显，而且增强后提取的海岸线位置准确度较高［7］。

本文选择大连长兴岛作为研究区，分别使用边缘检测法、阈值分割法及小波变化法进行海岸线提取，并对结果进行对比分析，获取最适合该区域岸线的提取方式。研究区域位于中国辽东半岛中西部，大连瓦房店市西侧，四面环渤海。全岛东西长30 km，南北宽11 km，环岛岸线91.6 km。全岛面积252.5 km2，为长江以北第一大岛，具有北方岛屿的典型特征，对研究长江以北岛屿岸线的提取有着重要的参考价值。

二、数据源及数据预处理

本文使用的数据源为大连长兴岛2008年4月15日的Landsat7 TM遥感影像数据，UTM投影，地面分辨率为30 m。使用同时段同区域高分辨率遥感航片作为基础图片，对提取结果的准确性进行比较验证。

为了排除在遥感影像获取过程中受到的各种因素的干扰，需要对遥感图像进行辐射定标、大气校正等预处理操作。同时，为了尽可能准确清晰地获得海岸线的地理信息，须对图像进行降噪、滤波及几何配准处理。

三、海岸线提取方法

1.阈值分割法

阈值分割法是一种最简单实用的影像特征提取方法，适用于要分割的物体与其背景有较强对比度的图像［8］。该方法的核心为图像的二值化。根据海洋与陆地在遥感影像中所呈现出的像素值差异，选取一个适当的特征阈值T，然后通过该阈值T与图像中逐个像素值进行对比，规定:若f(x，y)＜T，则g(x，y)=0，否则 g(x，y)=1。因此，阈值的选取成为该方法的关键点。

常用的阈值确定方式有直方图分割法及最大类间方差法等。其中最大类间方差法对于单一阈值的计算具有简单高效的方式，本文选择该方法，使用Matlab软件中graythresh函数及im2bw函数，确定图像的相应阈值并进行图像的二值化。同时，为了更有效地对海岸线进行提取，在二值化的过程中对图像进行边缘锐化。

2.边缘提取法

图像边缘指图像中灰度值急剧变化的像素集合，图像边缘处存在明显的灰度不连续性，变化情况可以用灰度分布梯度来反映。边缘检测法正是利用这种灰度值的差异，通过辨别每个像素与其邻域的状态，构建边缘提取算子，通过对邻域梯度进行计算来判断该像素是否在边缘上［9］。目前使用的经典的边缘提取算子主要有Roberts算子、Sobel算子、Prewitt算子和Canny算子等。

(1)Roberts算子

Roberts算子是根据任意一对相互垂直方向上的差分可用来计算梯度的原理，采用对角线方向相邻两像素灰度之差，即利用局部差分算子计算边缘。若输入图像为f(x，y)，输出图像为 g(x，y)，则利用Roberts算子进行边缘提取的过程可以表示为［10］

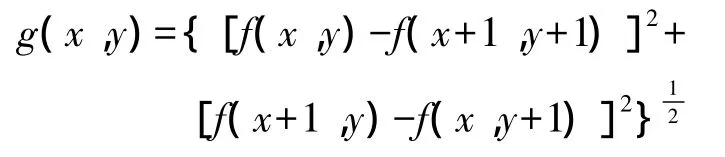
Roberts算子是一种较为简单的边缘提取算子，使用2×2模板，仅计算对角线上的梯度幅度，具有较高的精确度，但抗噪声能力较差。

(2)Sobel算子

Sobel算子计算每个像素值上下左右方位邻点的灰度加权差，以此确定像素点的梯度值，最后根据特定的阈值来进行取舍。

Sobel算子将2×2的模板扩展至3×3的模板，具有两个卷积核，受噪声影响比较小，当使用大的领域时，抗噪性能会更好，较容易在空间上实现，但同时也会产生许多伪边缘，边缘定位精度不高［11］。

(3)Prewitt算子

Prewitt算子与Soble算子类似，是一个含有两个卷积核的3×3的算子。中心像素梯度值利用周围8个点的像素值进行确定:在图像空间利用两个方向模板与图像进行邻域卷积，这两个方向模板一个检测水平边缘，一个检测垂直边缘［12］。具体表达式为

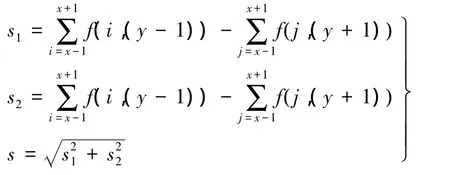
式中，s1、s2分别为Prewitt算子2个模板的卷积;s为所求像素的梯度值。

该算子在处理低噪声的图像时有较为明显的优势，但在处理混合多复杂噪声的图像时，效果较差。

(4)Canny算子

1986年Canny提出了边缘检测性能的3个准则:信噪比准则、定位精度准则和单边缘响应准则，基于这3个标准，一个多级边缘检测算法——Canny算子被提出，这是目前最优的边缘提取算子［13］。

Canny算子主要分为4个步骤:

1)利用高斯滤波对图像进行平滑处理。利用二维高斯函数的一阶导数对原始图像f(x，y)进行平滑去噪，得到平滑图像I(x，y)。在具体实现时，需要根据实际情况选择高斯滤波参数。

2)在2×2的邻域内进行差分运算，对平滑后的图像灰度梯度进行运算，像素点大小M和方向θ的计算公式为

式中，P、Q分别为该点x、y方向偏微分的一阶近似值，即

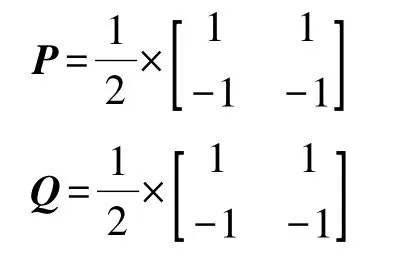
3)对梯度幅值进行非极大值抑制，只保留幅值局部变化最大的点。图像的梯度值与图像阵列的M(i，j)值成正比例关系，为确定边缘，必须通过抑制梯度方向上所有非屋脊峰值的幅值来细化幅值图像中的屋脊带。

4)边缘检测及边缘连接。这个过程使用双阈值法，选用高、低两个阈值对经过非极大值抑制后的图像作进一步处理，即凡是像素点的梯度幅度大于高阈值的一定是边缘点;凡是梯度幅度小于低阈值的一定不是边缘点。

Canny算子是目前边缘提取法中最为有效的一种算子，其提出的边缘提取准则在实际应用中获得了显著的效果，为今后的边缘提取工作提供了极大的参考价值。Canny算子自身具有很高的综合性，在提取边缘时可以很精确地计算出边缘像素。但由于Canny算子采用的是2×2的模板，在垂直邻域内对噪声较为敏感，容易造成假边缘，存在失真情况。同时，高低阈值限定无法顾及局部特征信息，致使边缘不连续的情况出现，且阈值的参数只能人为设定，使得Canny算子的自适应性不强，自动化程度低［14］。

3.小波变换法

小波变换法在数学领域中发展迅速，是1974年由法国工程师J.Morlet提出的，是一个时间和频率的局域变换，能够对信号进行多尺度的细化与分析，从而有效地从信号中提取信息。

设 f∈L2(R)，则其小波变换表示为［7］

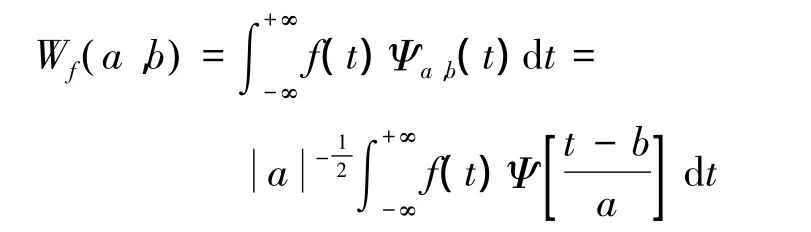
其重构公式为

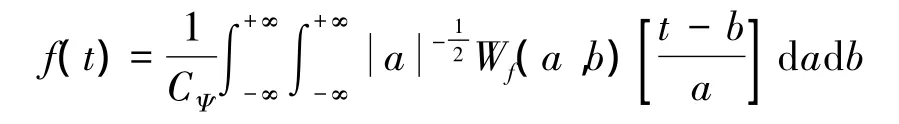
式中，ψ(t)∈L2(R)为母小波，其傅里叶变换φ(x)满足条件

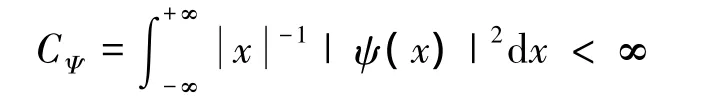
a、b分别为伸缩因子与平移因子，即母小波ψ(t)通过伸缩和平移后得到的小波序列为

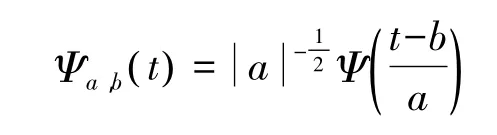
近年来，随着小波变换在边缘提取技术方面不断发展和完善，利用小波变换提取海岸线成为了一种新兴的水边缘提取方法。这种方法首先将海洋和陆地的灰度值转化为数字信号，在海陆交界处数字信号会有明显的奇异性(不连续性)，利用小波技术对这种数字信号进行分析，找出奇异点的位置，并把它们依次连接起来，确定海岸线［15］。

由于小波变换技术的时间频率局部精确化及空间多尺度的特性，小波变换在对图像水边缘检测时，一方面可以在小尺度范围内细化岸线，对岸线进行精细处理;另一方面，又可以在大尺度下粗化岸线，对在大尺度范围产生的假边缘有很好的处理效果，在保证岸线连续性的同时，极大地提高了海岸线的精确度。

四、结果与分析

1.研究结果

为验证几种试验结果的不同效果，本文使用ArcGIS软件对结果进行比较分析，利用与遥感影像同时段同区域的高分辨率遥感航片，与提取结果进行拟合对比。由于航片影像具有高分辨率性，地物特征表现得较为明显，能够清晰地观察出海陆界限，因此，通过对比航片影像图中海陆分界线与试验结果的重合效果，可以较为直观地看出几种不同方式的优劣性。拟合效果图如图1所示。

图1

通过试验结果拟合对比图可以得到如下结论:

1)阈值分割法对于海岸线的提取结果与真实地物差别最大，提取结果最粗糙。

2)边缘提取法中Roberts算子、Sobel算子及Prewitt算子的提取结果几乎相同。

3)小波变换法与Canny算子均能较为准确地提取出海岸线，与真实地物拟合程度较大。与其他方式的差异部分多为人工围海形成的养殖圈。在复杂海岸线处，小波分析法相较Canny算子呈现明显优势。

4)由于填海区域的灰度值与陆地灰度值差距较大，与海域灰度值差距较小，在对其海岸线确定时，存在较大的误差。几种提取方法中只有小波变换法与Canny算子能够对填海区域的海岸线进行提取。其中，Canny算子提取的结果精度更高，更适合研究人工围填海区域。

2.结果分析与展望

本文采用了ETM遥感影像对海岸线进行研究，利用多种方式对大连长兴岛海域海岸线进行提取，使用同一时期研究区域航片作为评估标准，对不同的海岸线提取方法进行了对比，结合ENVI、Matlab及ArcGIS等软件进行了研究分析与对比。研究结果显示，大连长兴岛海域最适宜使用小波变换法对其海岸线进行提取，而在对填海区域进行研究时，则适宜使用边缘提取法中的Canny算子。