基于相关系数迭代法的水下地形测量时间延迟探测方法研究

桂 新，秦海波，王胜平，陈晓勇

(1.江西省基础测绘院，江西 南昌330001;2.东华理工大学测绘工程学院，江西 南昌330013)

一、引 言

GPS定位技术的发展，尤其是高程定位精度的提高，使得借助GPS RTK及GPS PPK技术进行无验潮模式水下地形测量成为可能，近年来国内外在该方面的研究和实践取得了一定效果［1-2］。基于GNSS的无验潮模式水下地形测量，除了受仪器本身的测量精度影响外，GPS信号在传输及数据处理过程中的时间延迟也是影响其精度的一项重要因素。在后期数据处理时，时间配准的缺失或采用精度不高的时间延迟量值，都有可能导致融合结果达不到预期效果，从而导致水下地形点均存在一定的位置滞后性。现有文献在对水下测量中时间延迟的探测主要采用特征点往返测量法。该方法主要依赖水底特征点往返观测的距离差除以往返船速之后获得，而实际测量中难以保证两次观测为同一特征点，从而导致时延探测精度及稳定性不高。为此，本文研究了一种基于相关系数迭代法的水下地形测量时间延迟探测方法，采用两种信号序列一致性判断，以期进一步提高时延探测的稳定性。

二、时间延迟理论

1.理论基础

无验潮模式水下地形测量常采用GPS RTK技术，RTK的高程解可以监测船体的垂直运动。另外，IMU还可以提供监测船体垂直运动的涌浪参数(Heave)。尽管Heave的采样率较高(5 Hz、10 Hz、50 Hz)，GPS的采样率较低(通常设置为1 Hz)，但两者除存在时间偏差外，所呈现的船体垂直运动仍具有非常好的一致性(如图1所示)。

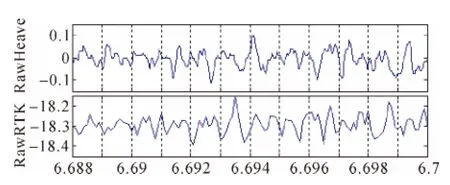
图1 Heave信号与GPS RTK信号垂直方向具有形态相似性

基于上述物理原理，根据HGPS及HHeave所反映的测量船在垂直方向上的运动波形的吻合程度，可以计算出时间延迟量。此时吻合程度的判断成为解决问题的关键。

本文选择相关系数ρ作为计算两种信号最吻合指标，来判断波形的吻合程度。

2.相关系数

在概率论与数理统计中，对于二维随机变量(X，Y)，如果两个随机变量X和Y是相互独立的，则E{［X－E(X)］［Y－E(Y)］T}=0;如果 X 和 Y不相互独立，而是存在一定的关系，则 E{［X－E(X)］［YE(Y)］T}≠0。

随机变量X与Y的协方差为

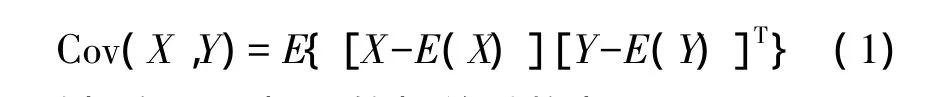
随机变量X与Y的相关系数为

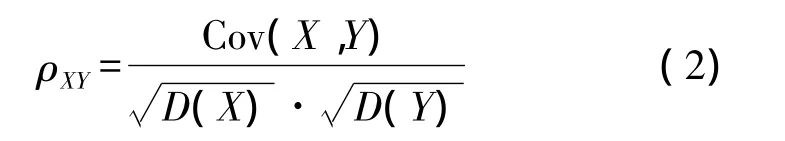
式中，D(X)、D(Y)分别是随机变量X与Y的方差，D(X)=E{［X－E(X)］2}，D(Y)=E{［Y－E(Y)］2}。

HGPS与HHeave同时反映了船体在垂直方向的运动状态，因此二者不是相互独立的，而是存在一定的关系。根据上述理论，由式(1)和式(2)可以得出随机变量HGPS与HHeave的相关系数

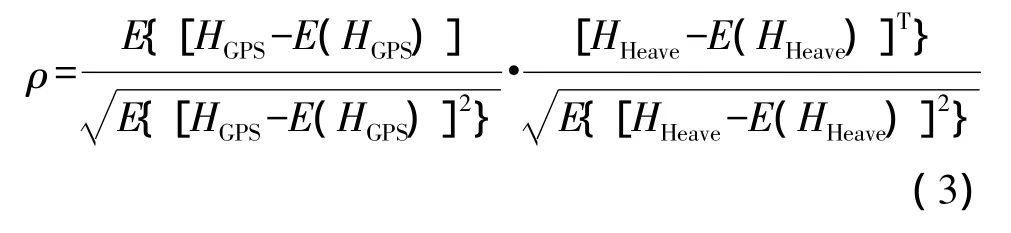
根据相关系数的特性可知，当|ρ|较大时，HGPS与HHeave的线性相关程度较好，特别当|ρ|=1时，HGPS与HHeave之间以概率1存在着线性关系;当|ρ|较小时，HGPS与HHeave的线性相关程度较差，特别当|ρ|=0时，HGPS与 HHeave不相关。事实上，随机变量HGPS与 HHeave的相关系数|ρ|≤1，当 |ρ|越趋近于 1时，HGPS与HHeave相关程度越好。

3.相关系数迭代法原理及流程

GPS RTK数据和IMU数据有各自的时间标志，分别记作TGPS和THeave，由于存在时间延迟，记作Δt，TGPS和THeave之间的关系为

时刻TGPS对应的GPS高程为HGPS，时刻THeave对应的IMU的涌浪(Heave)值为HHeave。利用相关系数法，求取时间段(t1，t2)内的随机变量HGPS和HHeave的相关系数ρ，根据|ρ|向1的趋近程度，判断HGPS和HHeave的相关程度。为了求解最佳的时延量Δt，需要赋给Δt一个初值并计算其对应的相关系数|ρ|，然后迭代计算比较相邻两次|ρ|，每次迭代给Δt累加一个时延步长，直至|ρ|最接近于1，迭代结束。利用迭代方法计算最佳的时延量Δt时，记时延步长为t。假设迭代次数为n时，|ρ|与1最接近，HGPS和HHeave的相关程度最好，此时时延量Δt与时延步长t存在如下关系

利用迭代方法求取时延量Δt的流程如图2所示。

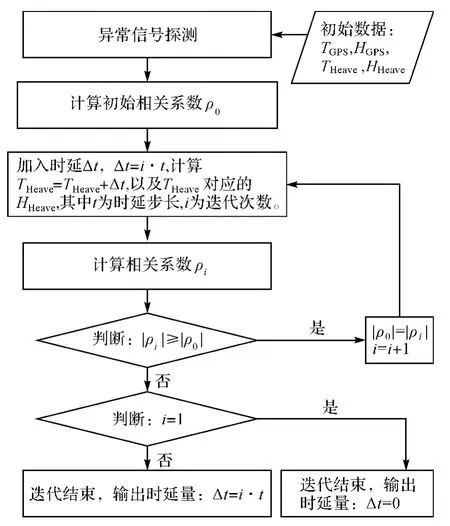
图2 迭代求取时延量Δt流程

三、试验结果及可靠性分析

为了论证本文所述理论的准确性与可靠性，在珠海海域进行了试验，试验中用GPS RTK模式测量瞬时水面高程，RTK模式采用人为架设基准站，其接收机为 Trimble SPS852。流动站接收机为1台Trimble SPS882，采样频率为1 Hz，数据采集期间，严格监视Trimble手簿，确保其始终处于“固定”状态。天线固定在测船上方开阔位置，易于观测且可以避免多路径效应的影响。IMU姿态传感器安置在船体中央位置(即测船重心位置)，IMU的采样频率设置为10 Hz。压力传感器安置在测船底部，采样频率设置为5 Hz。试验期间，姿态传感器和压力传感器数据通过自主编写的数据采集软件采集和存储。

基站架设在深圳湾航道站附近的航道站控制点，测量开始前将测船锚定(认为测船处于静止状态)，在岸边架设徕卡全站仪TCR802，用棱镜模式测定姿态传感器(位于船体重心处)和GNSS接收机，获得船体坐标系下测船初始姿态坐标，见表1。

表1 传感器在船体坐标系下的坐标 m

试验中采用高斯投影坐标系，中央子午线为114°，投影比例因子为1。水尺验潮时，由已知水准点通过水准观测引测至岸边临时验潮站，观测期间进行人工验潮数据采集。

通过本文所述方法对试验数据进行了时延探测，原始数据中RTK高程信息HGPS和TSS的涌浪参数HHeave在垂直方向的运动波形如图3所示。由于原始数据数据量过大，不利于分析试验效果，因此截取了运动波形有明显变化的时间段内的数据来计算时延量，截取的数据如图4所示。

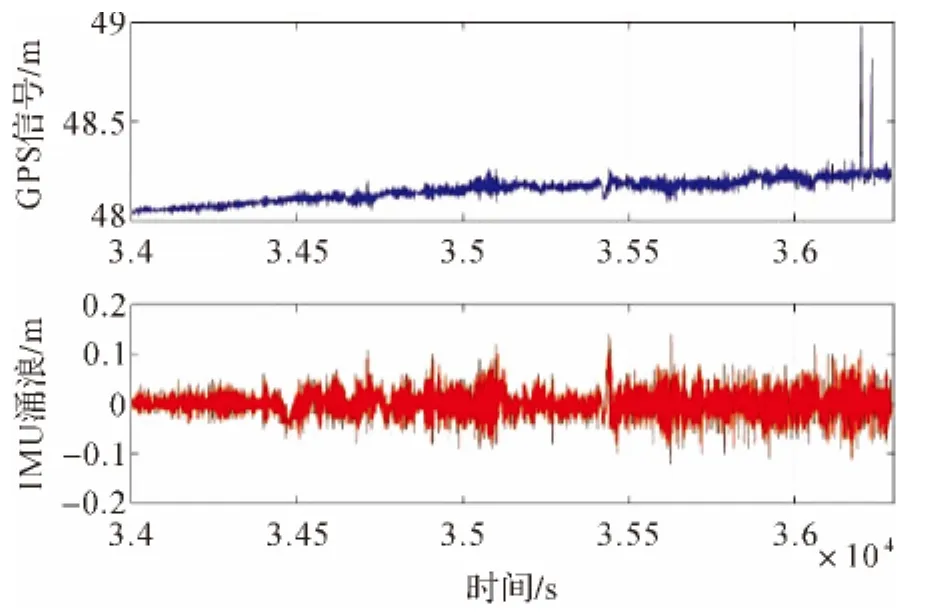
图3 原始RTK高程数据和IMU涌浪数据

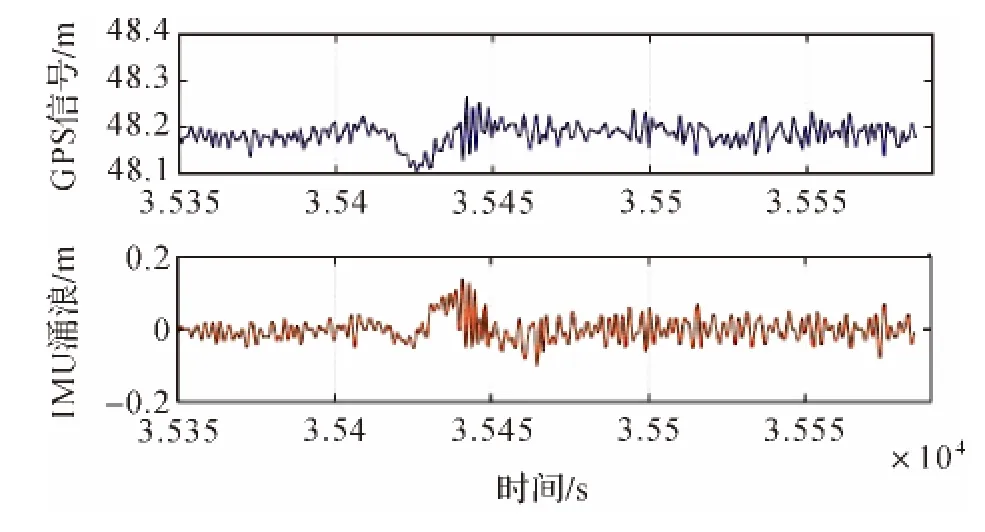
图4 截取的运动波形有明显变化的数据

试验时延步长设置为0.1 s，最终计算得到的时延量为0.8 s，对应相关系数为 0.684。时延量和对应的相关系数见表2和图5。

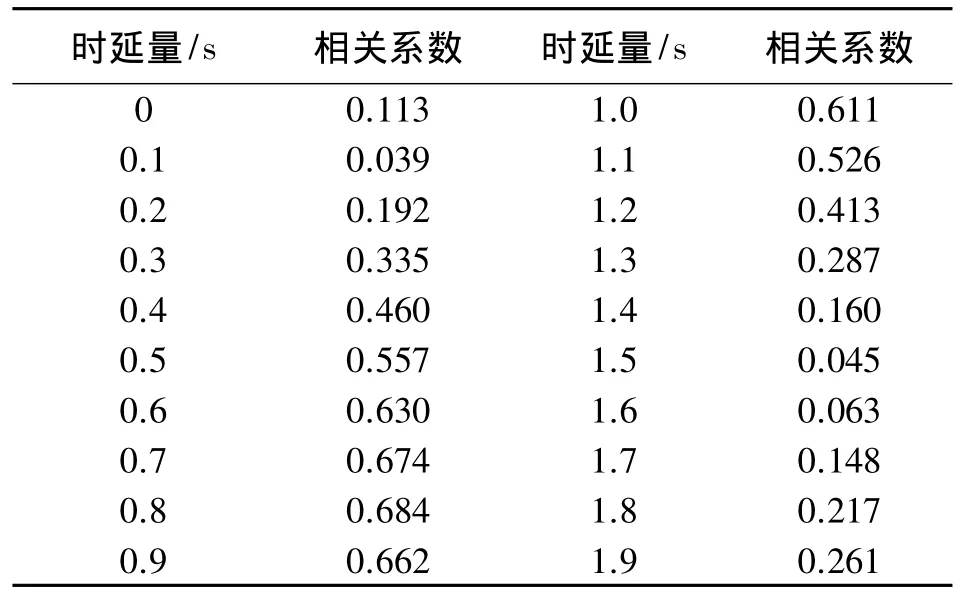
表2 时延量及其对应的相关系数列表

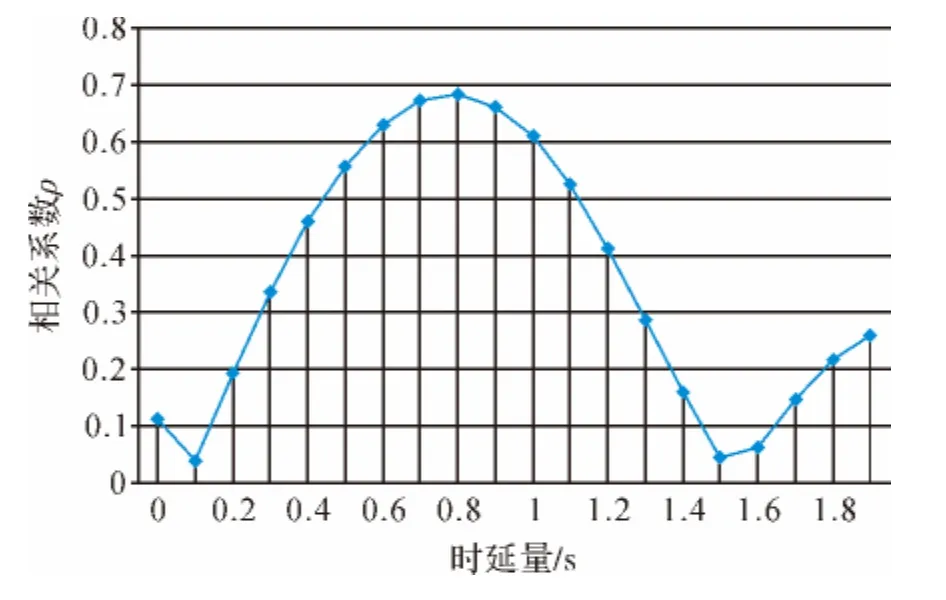
图5 时延量及其对应的相关系数列表

经过时延改正后RTK高程和IMU涌浪的运动波形吻合程度较好，如图6所示。

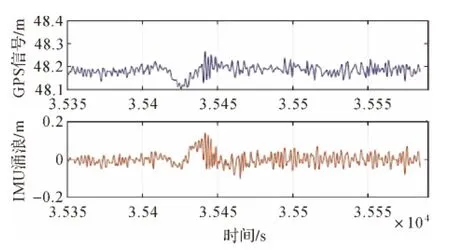
图6 时延改正后RTK高程数据和IMU涌浪数据

四、结束语

经过时延改正后，RTK高程信息和IMU涌浪信息所反映的船体垂直方向运动波形得到了很好的吻合。本文采用相关系数连续迭代计算求解最佳时延量，可以根据不同情况，选择不同的时延步长，时延步长值越小，最终获得的时延量越精确。通过对RTK高程信息和IMU涌浪信息所反映的船体垂直运动波形分析比较，证明了本文所述方法的正确性。

［1］董江，王胜平.GPS PPK远距离在航潮位测量及其在航道的实现［J］.测绘通报，2008(5):51-53.

［2］ZHAO Jianhu，HUGHES J E C，BRUCKER S，et al.Onthe-fly GPS Tide Measurement along Saint John River［J］.International Hydrographic Reviewer，2004，5(3)，48-58.

［3］赵建虎，周丰年，张红梅.船载GPS水位测量方法研究［J］.测绘通报，2001(S1):1-3.

［4］MANN D.GPS Techniques in Tidal Modeling［J］.The International Hydrographic Review ，2007，5(2):59-71.

［5］赵建虎，刘经南，周丰年.GPS测定船体姿态方法研究［J］.武汉测绘科技大学学报，2000，25(4):353-357.

［6］赵建虎，张红梅，HUGHES J E C.测船处瞬时潮位的GPS精密定位［J］.武汉大学学报:信息科学版，2006，31(12):1067-1070.

［7］张振军，谢中华，冯传勇.RTK测量精度评定方法研究［J］.测绘通报，2007(1):26-28.

［8］阳凡林，赵建虎.GPS验潮中波浪的误差分析和消除［T］.海洋测绘，2003，23(3):1-4.

［9］桑金.基于GPS技术的水深归算法［J］.测绘通报，1999(8):23-25.

［10］赵建虎，王胜平，张红梅，等.基于GPS PPK/PPP的长距离潮位测量［J］.武汉大学学报:信息科学版，2008，33(9):910-913.