超宽巷组合下的北斗三频TurboEdit方法研究

邵 奎，白征东

(清华大学土木工程系地球空间信息研究所，北京100084)

一、引 言

在采用载波相位进行数据处理时，周跳的探测一直是数据预处理中比较棘手的问题。如果周跳未能被准确探测或未得到有效恢复，势必影响模糊度的确定及定位的精度。周跳的探测与修复可为后续的数据处理提供高质量的数据源。一种正确、高效的周跳探测与修复方法可以为正确地求解模糊度，进而得出高精度的定位结果奠定基础。周跳探测与修复的基本思路就是通过合理的数据处理，得出精确反映周跳变化的检测量序列，从检测量序列中探测出周跳发生的位置和大小并修复，最后将周跳改正后的数据序列参与解算［1］。目前比较常用的周跳探测与修复方法主要有差分法、电离层组合法、多项式拟合法、线性拟合法等。本文在Blewitt提出的TurboEdit方法［2］的基础上，结合北斗三频观测数据的特点，提出了一种基于超宽巷组合的TurboEdit方法，并利用实测数据对此方法作进一步的分析。

二、宽巷TurboEdit方法

宽巷TurboEdit方法根据双频观测值的组合特性，选取两组周跳检验量，分别是宽巷组合检验量和无几何距离组合检验量，可以有效地探测和修复周跳。

伪距和载波相位的基本观测方程为

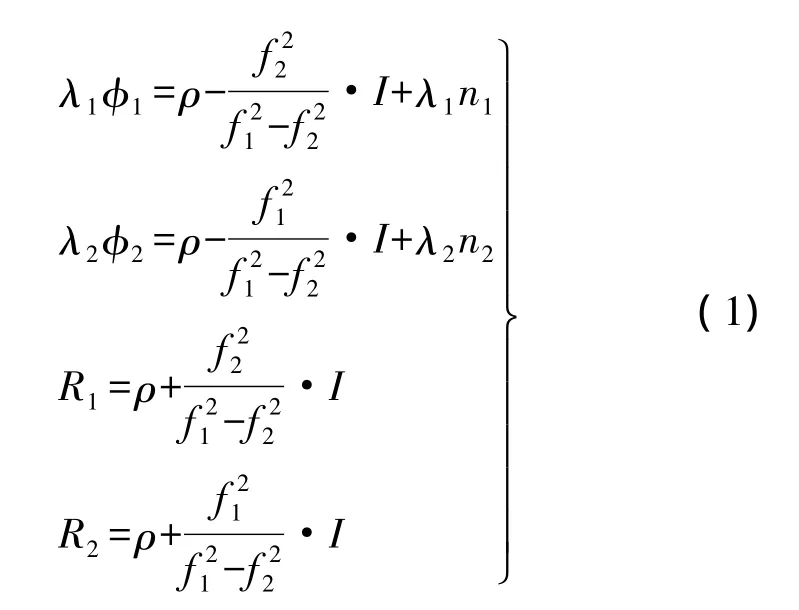
式中，ρ为卫星到接收机的几何距离;I为B1载波上的电离层延迟;n为整周模糊度。

Melbourne-Wübbena(M-W)宽巷组合公式及其整周模糊度可表示为

式中，L表示以m为单位的相位观测量;λmw表示组合波长;c表示光速。

通常情况下，对于一个无周跳的观测时段，bw表示宽巷组合的整周模糊度项，应接近于常数，并且随机分布，一旦发生宽巷周跳，则bw的分布曲线会出现相应的跳变。为此可构建周跳检验量ΔN4

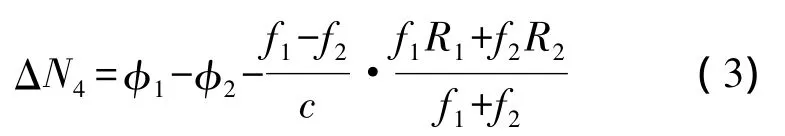
在单历元算法中，采用递推公式计算每一历元i的周跳检验量预测值〈ΔN4〉i及其方差

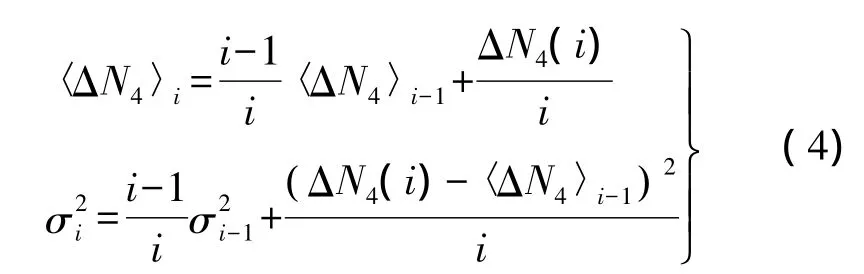
对第1个历元取σ1=0，若4σi，则认为i+1历元可能发生周跳;继续判断i+2历元的状态，若，则认为历元i+1有周跳;若，则认为历元i+1为野值。

当两个频率同时发现相同的周跳时，利用MW方法无法有效地进行周跳的探测。因此还需要构建一组有别于宽巷组合的双频组合观测值，通常采用无几何距离组合观测值［3］

即电离层残差法对应的组合公式，根据式(3)和式(5)计算出ΔN4和ΔL，联立方程可求解B1和B2载波上各自的周跳值。

对于北斗三频数据，构建3组宽巷组合(1，－1，0)、(1，0，－1)和(0，－1，1)，对应的波长分别为 0.847 m、1.025 m 和 4.884 m，可采用 TurboEdit方法依次进行周跳的探测与修复。数据使用2013年5月10日的北斗三频观测数据，采样间隔1 s，取观测开始2 h后的1000个历元的观测数据进行试验。

图1、图2、图3分别给出了 3组宽巷组合的TurboEdit检验量的时间序列，在第50—80历元的B1、B2、B3上分别增加5周、1周、1周的周跳。

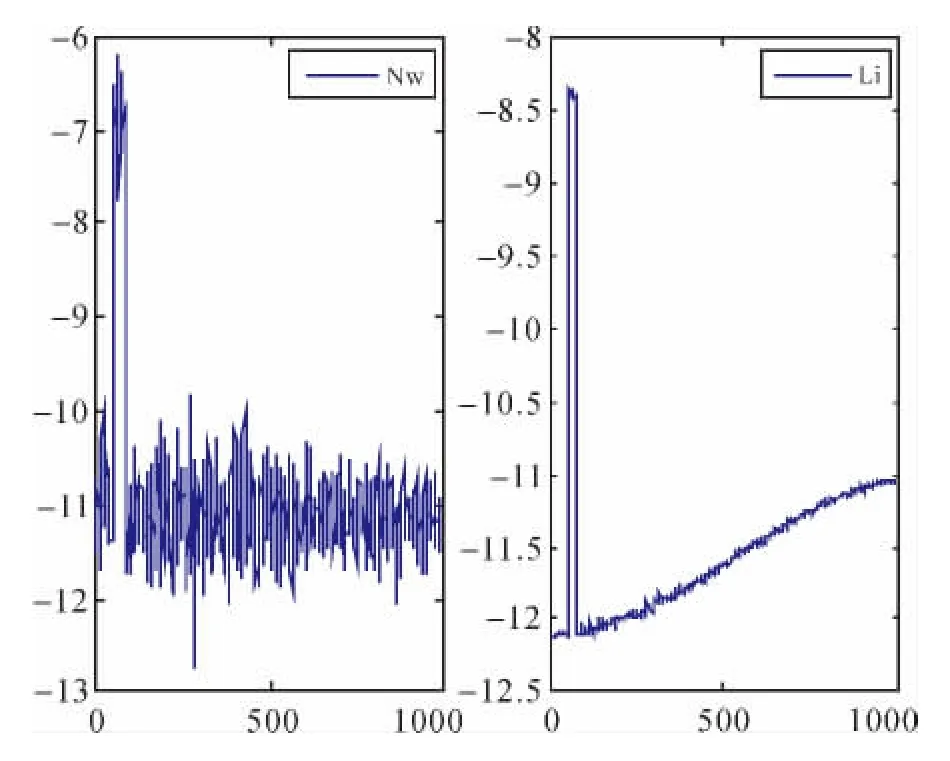
图1 N1-N2的TurboEdit检验量

从图1和图2中的周跳检验量ΔN4和ΔL分布图中可以明显看出，第50—80历元的检验量有明显的突变，利用TurboEdit方法可探测并解出B1、B2、B3 上的周跳值分别为 5、1、1。

从图3中的周跳检验量ΔN4和ΔL分布图中无法明显地看出第50—80历元的检验量有明显的突变，而且利用TurboEdit方法也无法探测出B1和B2上各自1周的周跳值。分析3个频率的伪距观测噪声(对伪距观测值作三次差)［4］，如图4所示。

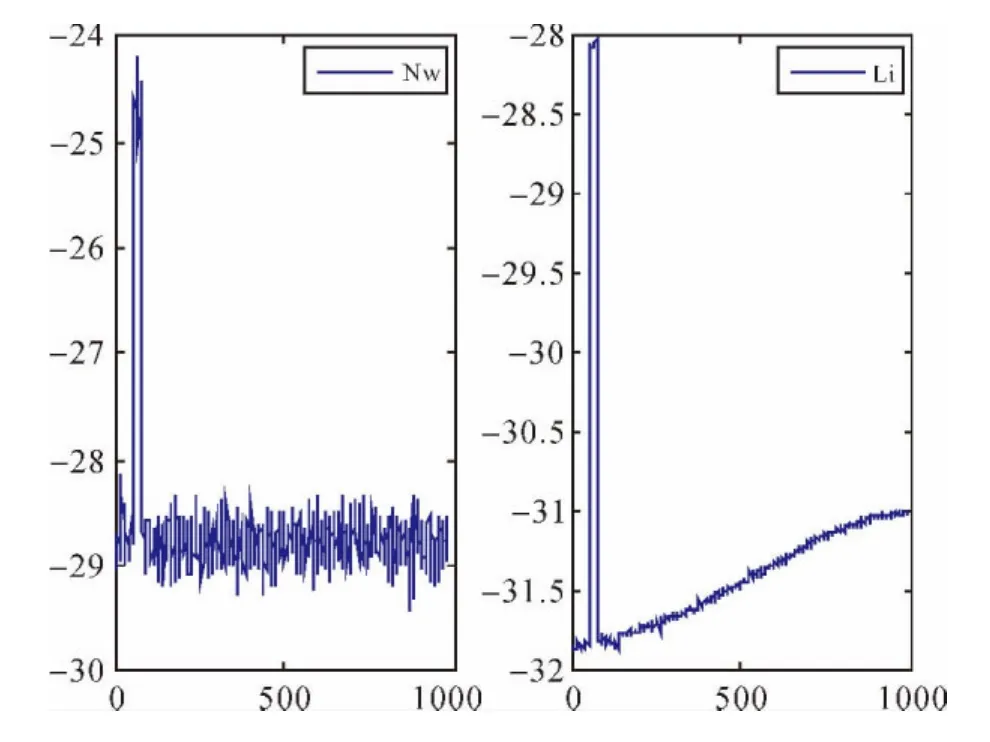
图2 N1—N3的TurboEdit检验量

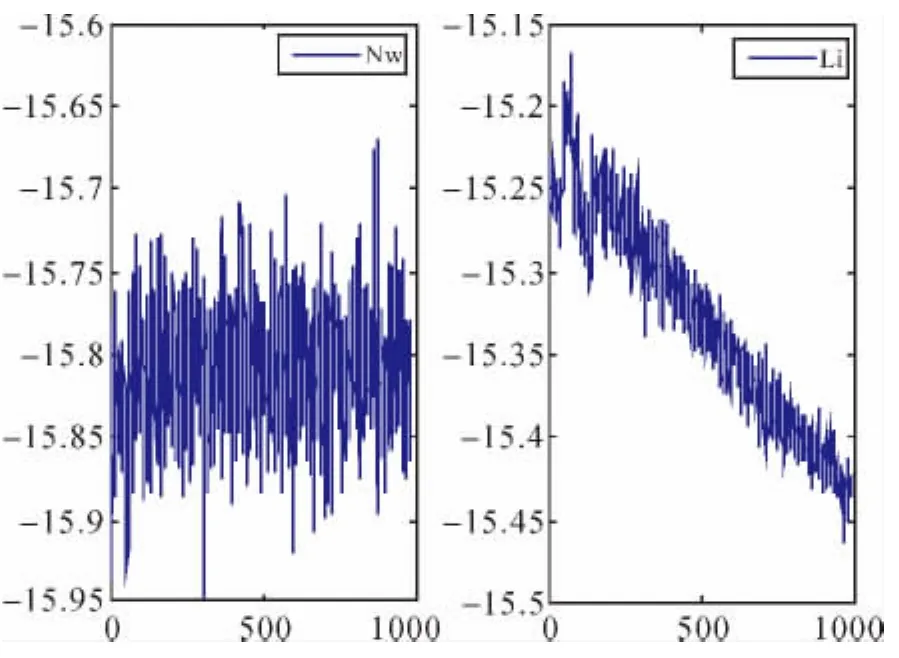
图3 N2—N3的TurboEdit检验量

图4 3个频率上的伪距观测噪声分布

从图4中可以看出，B2的伪距观测噪声为1.053 4 m，明显高于 B1 和 B3，此时在 TurboEdit方法中构建带有B2和B3伪距的(0，－1，1)宽巷组合时，由于B2伪距较大误差的影响，B2和B3载波上1周的周跳被伪距噪声所掩盖，结果导致无法利用TurboEdit方法有效地进行周跳的探测与修复。

综上所述，利用基于宽巷组合的TurboEdit方法进行北斗三频数据的周跳探测与修复时，需要进行3次数据处理，而且若某一个频率的伪距噪声较大时，无法有效地进行周跳的探测。

三、基于超宽巷组合的北斗三频TurboEdit方法

为了降低单一频率上伪距噪声的影响，并减少重复的数据处理，本文结合三频组合观测值的长波长特性，提出了一种基于超宽巷组合的TurboEdit方法，其原理如下:

针对北斗观测数据，选取两组属性较好的超宽巷组合 LE(0，－1，1)和 LF(1，4，－5)［5］，构造相应的周跳检验量ΔNE和ΔNF

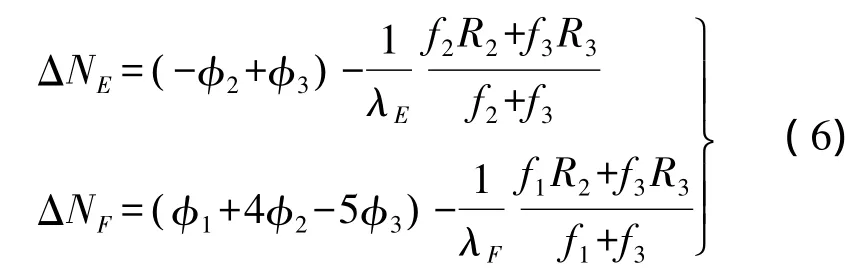
在单历元算法中，采用递推公式计算每一历元i的周跳检验量预测值及其各自的方差

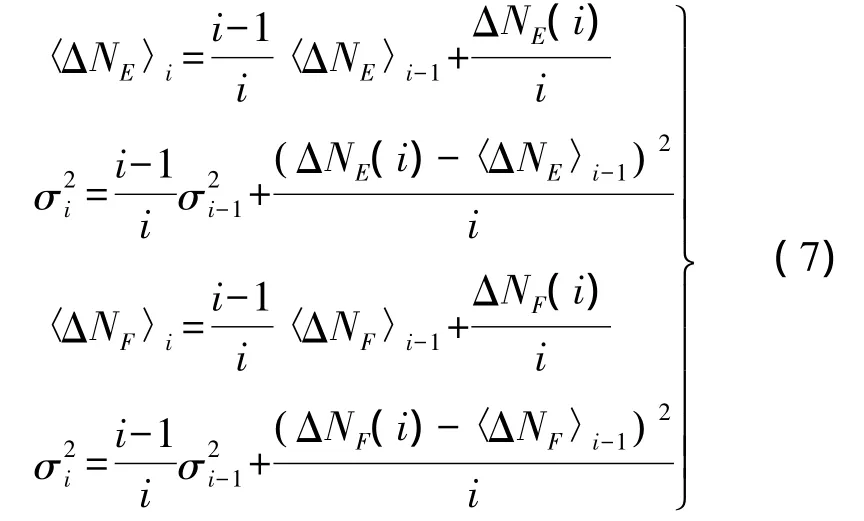
对第1个历元取 σ1=0，若4σi且，则认为 i+1 历元发生周跳或粗差。

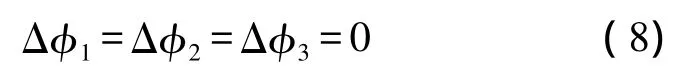
即，当3个频率中有两个频率出现相同的周跳时，利用两组超宽巷组合无法进行周跳的探测，此时需要增加无几何距离组合。只要进行任意两个频率的检验后，第3个频率的周跳存在情况可直接确定，因此无几何距离组合周跳检验量可构建为

这种基于两组超宽巷组合的TurboEdit方法只需一次处理即可探测3个频率的周跳值，一个频率的伪距噪声较大时仍能进行周跳的探测与修复，有效地增强了算法的可靠性。为了验证算法的准确性，仍然采用上述宽巷TurboEdit方法的北斗数据，在第50—80历元的3个频率上分别增加5、1、1周的周跳，周跳检验量的分布如图5所示。

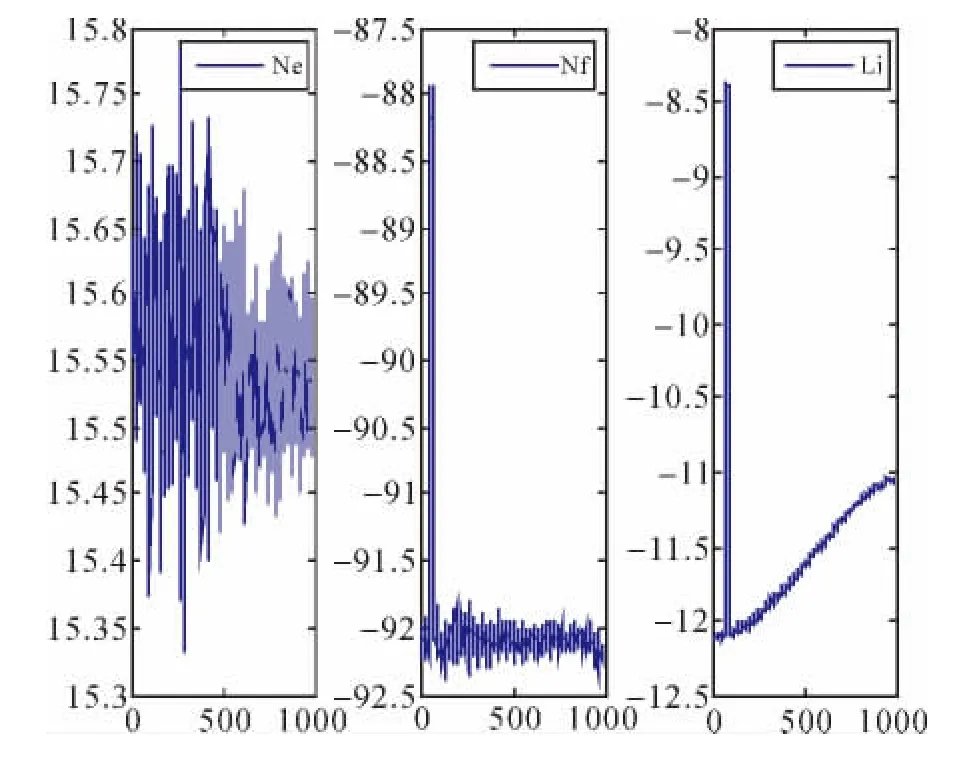
图5 基于超宽巷组合的TurboEdit检验量序列

从图5中的周跳检验量NF和L分布中可以明显看出，在第50—80历元的检验量有明显的突变，计算可得3组周跳检验量的结果分别为ΔNE=0，ΔNF=4，ΔL=3.707 6，联立方程组解得 3 个频率上的周跳分别为 ΔN1=5，ΔN2=1，ΔN3=1。

从实例结果中可以看出，基于超宽巷组合的TurboEdit方法可以准确地探测出3个频率上的周跳，而且处理三频数据只需要进行一次运算，同时超宽巷方法综合利用了3个频率的数据，有效地降低了单个频率伪距噪声的影响，增强了算法的可靠性。

四、结束语

本文在宽巷TurboEdit方法的基础上，结合北斗三频超宽巷组合的长波长、弱电离层延迟特性，设计了针对超宽巷组合的周跳检验量，综合利用3个频率的伪距和相位数据，不仅能准确地探测并修复周跳，而且有效地降低了单个频率伪距噪声的影响，增强了周跳探测的可靠性。

［1］雒卫民，陈义.用TurboEdit方法对GPS观测数据进行周跳探测［J］.铁道勘察，2006，32(4):3-5.

［2］BLEWITT G.An Automatic Editing Algorithm for GPS Data［J］.Geophysical Research Letters，1990，17(3):199-202.

［3］王维，王解先，高俊强.GPS周跳探测的方法研究［J］.武汉大学学报:信息科学版，2010，35(6):687-690.

［4］王应东.GPS误差分析和精度控制［J］.测绘与空间地理信息，2011，34(6):235-236.

［5］FENG Y.GNSS Three Carrier Ambiguity Resolution U-sing Ionosphere-reduced Virtual Signals［J］.Journal of Geodesy，2008，82(12):847-862.