机动飞行器三维运动制导误差计算方法研究*

郝 颖，周 华，陈升泽

(中国运载火箭技术研究院研发中心，北京 100076)

0 引言

为降低被拦截的概率，新概念飞行器的弹道模式呈现纵向和侧向机动的特性，气动外形也由轴对称向面对称转化。例如，以美国FALCON计划中的CAV(common aero vehicle，CAV)为例，非常规的助推-滑翔-跳跃飞行轨迹，以及远距离的横纵向机动能力，使其较难以预测、跟踪及拦截。针对此类型飞行器，传统的基于射面内、侧向运动与偏航、滚动程序角为零的环境函数法不再适用于此类飞行器制导误差的计算分析。鉴于此，文中引入弹道求差法的概念，针对捷联惯导系统的误差模型，进行了机动弹道模式下，制导工具误差计算的推演并对其应用结果进行了讨论。

1 环境函数法与弹道求差法

对于常规弹道模式而言，在质点弹道计算过程中将偏航与滚转方向的程序角ψ、γ设定为零，对应着姿态角速度在弹体系下的投影量ωy1与ωx1的值很小。对于采用光学陀螺捷联惯导系统而言，其陀螺仪误差模型的激励仅由俯仰方向的角速率构成;此外，ψ=γ=0还直接导致了由弹体系到发射惯性系方向余弦矩阵的大幅简化;对于石英加速度计误差模型而言，弹体上轴向的视加速度由于推力的作用，远大于纵向与侧向的视加速度，因此的值亦可忽略，加速度计误差模型的激励也仅与轴向视加速度有关。在上述的多种简化条件下，才得以求出由单位惯性器件误差系数引起的速度与位置误差的环境函数，并利用其结果进行落点偏差的计算［2］。其计算过程的原理框图如图1(a)所示。

但是，上述的简化形式仅适用于助推+自由抛物线的传统弹道形式，其制导系统仅在主动段发挥作用;对于AHW类的机动弹道形式，制导系统几乎需要全程工作，可能在非主动段中，惯性器件的误差模型在纵向与横、侧向均要受到线加速度与角速度的激励(例如需要完成BTT机动控制动作)，那么在进行制导误差的估计过程中，惯导系统的误差模型各项系数和方向余弦矩阵各元素均不可以简化，需要进行复杂的矩阵相乘过程，导致无法提炼出位置、速度误差与单位误差系数间的环境函数表格，不能采用式(1)的形式进行制导误差的估计，因此，需要通过在瞬时三维标准弹道视加速度基础上叠加加速度计与陀螺仪产生的加速度误差，通过产生的偏差弹道落点与标准弹道落点相比较来获得飞行器落地的横纵偏差。弹道求差法计算射程与横向偏差的基本原理如图1(b)所示。

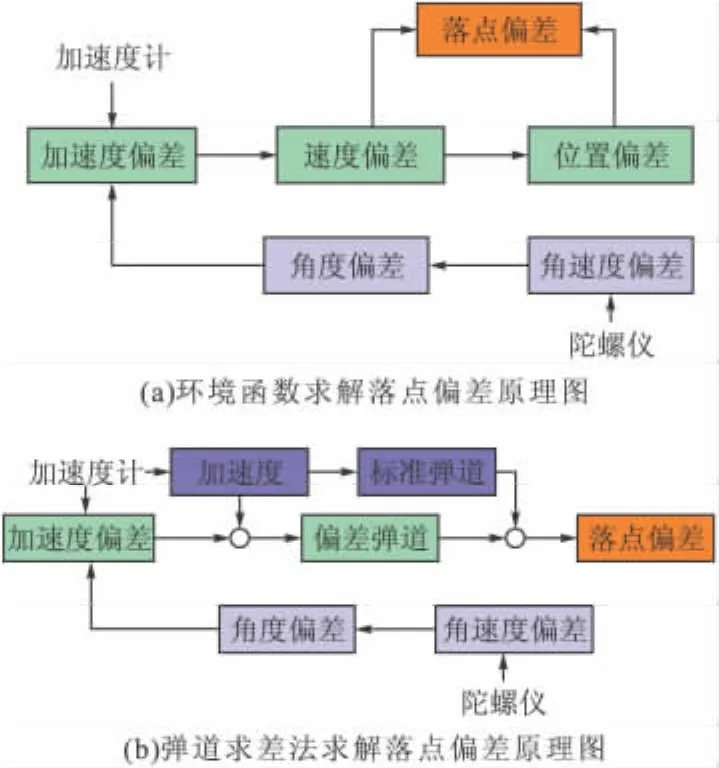
图1 环境函数法与弹道求差法求取落点偏差的方法

2 机动弹道制导工具误差模型

以飞行器控制系统采用的捷联惯性测量组合为例，在机动弹道模式下，与弹体相捷联安装的加速度计产生的视加速度偏差为:

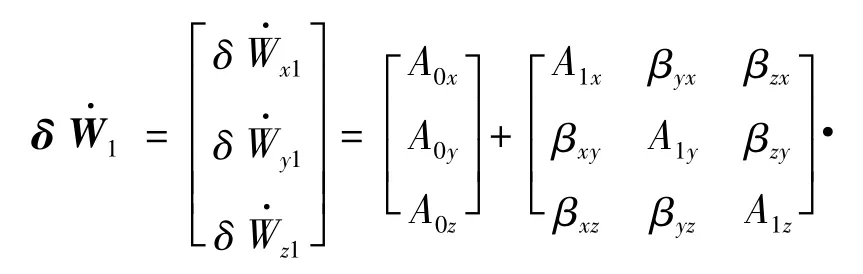
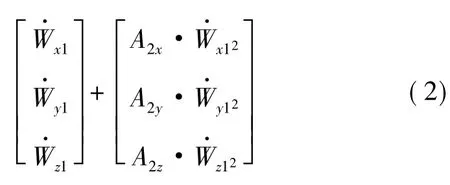
其中:A0i、A1i、A2i(i=x，y，z)分别为加速度计的常值漂移项和与视加速度有关的一次、二次项误差系数;βij(i，j=x，y，z，i≠j)为 3 个加速度计分别沿弹体3个轴的轴向安装误差角系数。

在制导误差计算过程中，将式(2)转换到发惯系下:

A即为由弹体系到惯性系转换的方向余弦矩阵。

惯测组合中，光学陀螺测量角速度的误差模型为:

进而得出发惯系下的角速度偏差为:

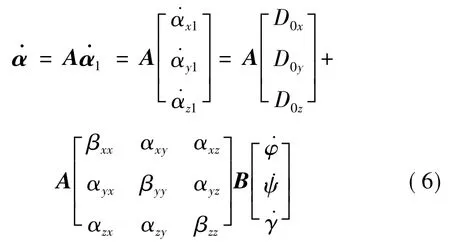
惯性系下的角度偏差(姿态失调角)为:

根据失调角(αx，αy，αz)按式(8)来计算惯性系视加速度偏差:

综合加速度计与陀螺仪的作用，视加速度的偏差可以定性表示为:

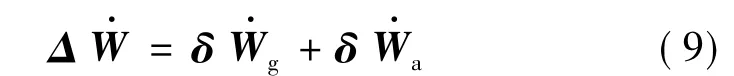
在进行与制导工具误差有关的偏差弹道计算过程中，需要把飞行器的运动方程写成如下形式:

3 仿真计算示例

3.1 算例1

以某飞行器再入段无机动弹道数据为计算依据，利用已经具有的“射面内运动制导工具误差计算方法”(简称一维算法)和上文推导的“机动弹道制导工具误差计算方法”(简称三维算法)进行惯性器件随时间累计的误差计算，以校核后者的准确性。对于计算程序而言，需要在一维计算的基础上，增加并处理法向、侧向的视加速度和相对于发射惯性系的偏航、滚转姿态角数据;由于不涉及弹道设计的中间过程，因此计算方法与倾侧角、侧滑角和侧向力等与产生机动的特殊变量无关。

设定飞行器采用固态陀螺仪构成的捷联惯组，陀螺仪及加速度计精度优于惯性级水平。根据一维、三维算法得出的再入段惯组累积的与陀螺仪有关基准误差和与加速度计有关的测速误差如表1、表2所示。

从表1、表2所示的计算结果可见，在一维的再入段弹道输入基础上，一维和三维的误差计算方法所得的横向偏差ΔH、纵向偏差ΔL的结果略有差异。一方面，表1中，两种方法对于由陀螺仪漂移产生的基准误差计算结果完全相同，一维算法下忽略的误差项由于一维运动无偏航与滚转角的激励而在三维算法下的计算结果为零，这说明对于基准误差的计算，一维算法是一种无损的简化。另一方面，通过对表2中由加速度计产生的测速误差计算结果对照可以看出，先前的一维计算方法是一种有损的简化，对于常规的主动段制导分析来说，由于轴向大推力的显著作用，使法向视加速度输入完全可以忽略，但是对于再入段来说，由于轴法向视加速度量值相当(如图2所示)，因此即使飞行器再入也不偏离射面，一维的计算方法由于忽略了法向视加速度对 A1y、A2y、Byx、Byz等误差系数项的激励，其算法是不精确的。由上述对照分析可以得出，三维的算法不仅适用于飞行器的三维机动弹道，也适用于不偏离射面内的弹道，且其算法计算结果更趋严谨。

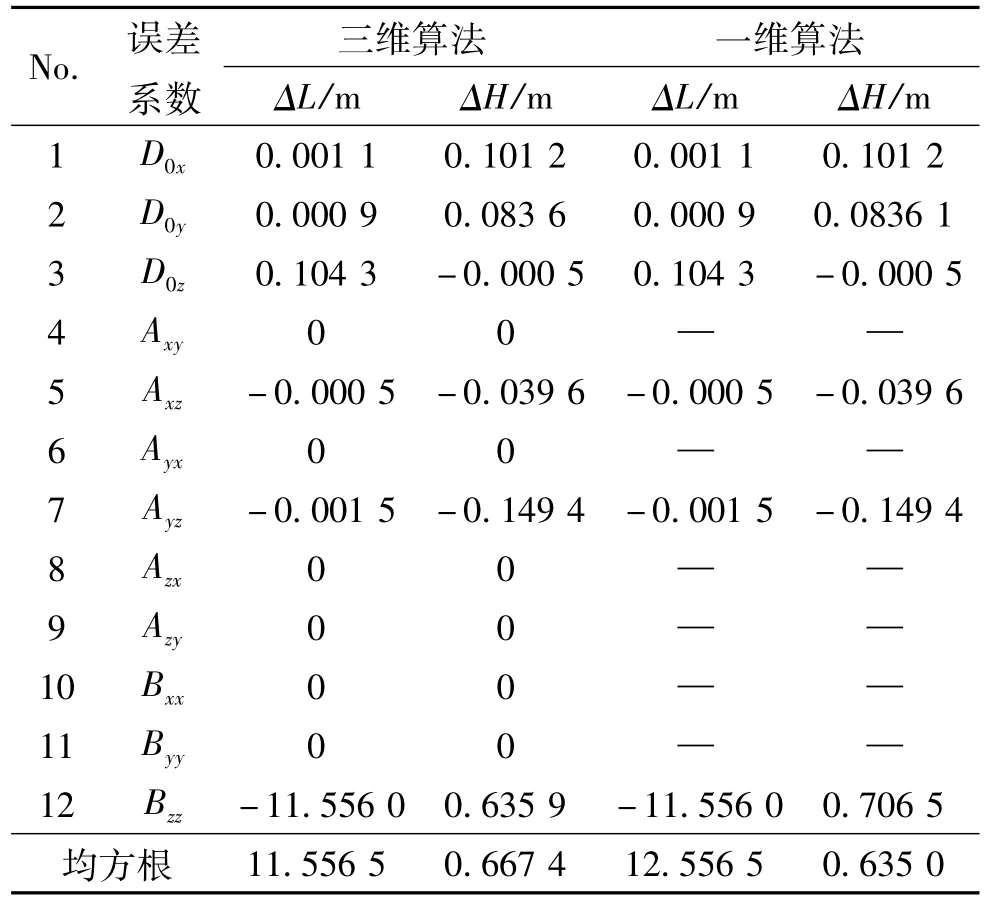
表1 再入段惯组的基准误差

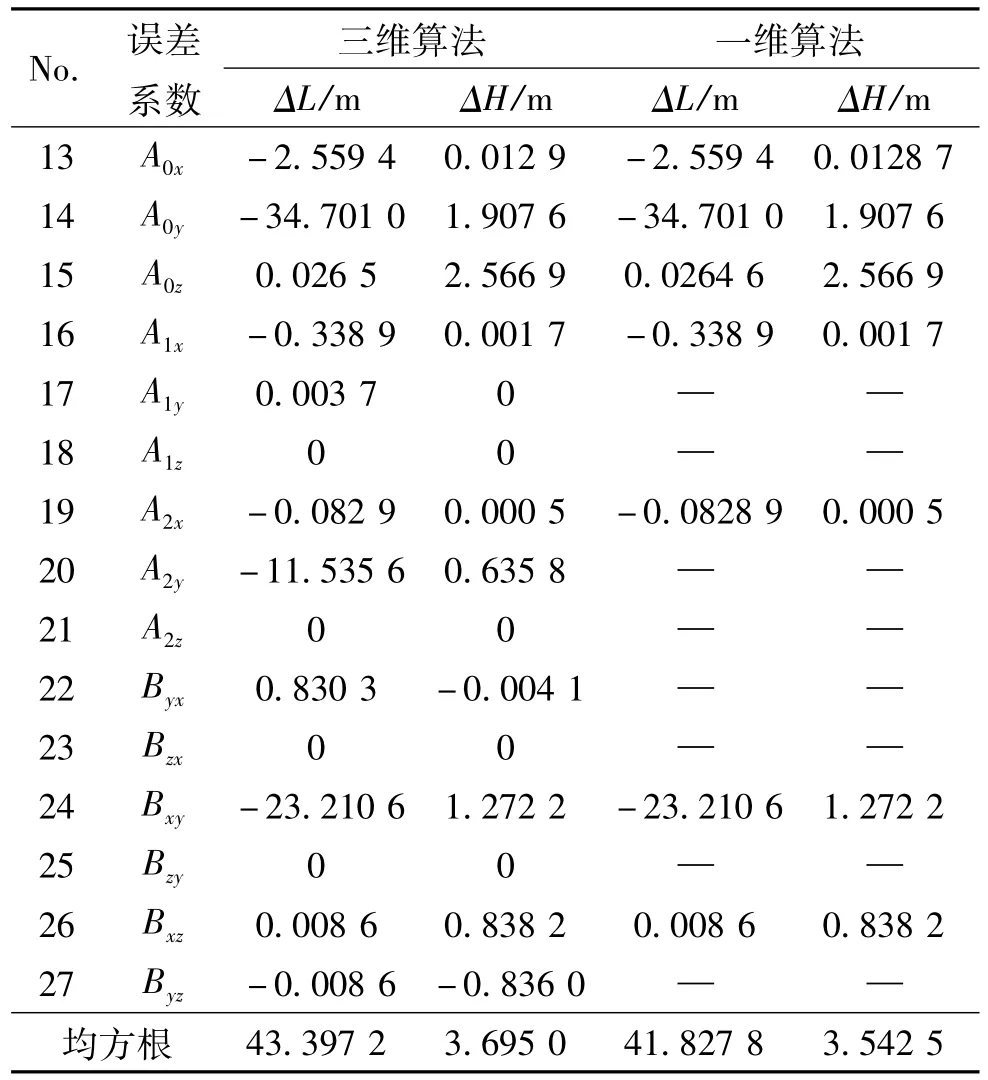
表2 再入段惯组的测速误差

3.2 算例2

利用经上述检验的制导系统误差三维算法对下面全程机动的飞行轨迹进行计算。图3、图4中所示的非零侧向视加速度和偏航与滚转程序角体现了显著的机动特征。

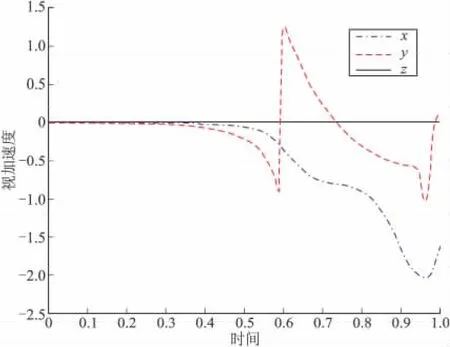
图2 再入段归一化视加速度分量曲线

图3 全程机动飞行器归一化视加速度分量曲线

图4 全程机动飞行器归一化姿态角分量曲线

设定飞行器采用与上文精度水平相同的捷联惯组，根据三维算法得出的全程机动飞行器制导系统累积的误差如表3、表4所示。

将表3中的第4、6、8～11项与表1相应项相对照，可以明显地看到滚转和偏航角速度对 Axy、Ayx、Azx、Azy、Bxx、Byy误差系数的激励作用，且其作用效果对基准误差的贡献显著。同理，将表4中第18、21、23、25项与表2相对照，也可以反映出侧向视加速度对加速度计误差模型中的A1z、A2z以及安装误差Bzx、Bzy误差系数的激励，由于z向视加速度幅值较小(如图3)，其对测速误差的最终计算结果影响较小。

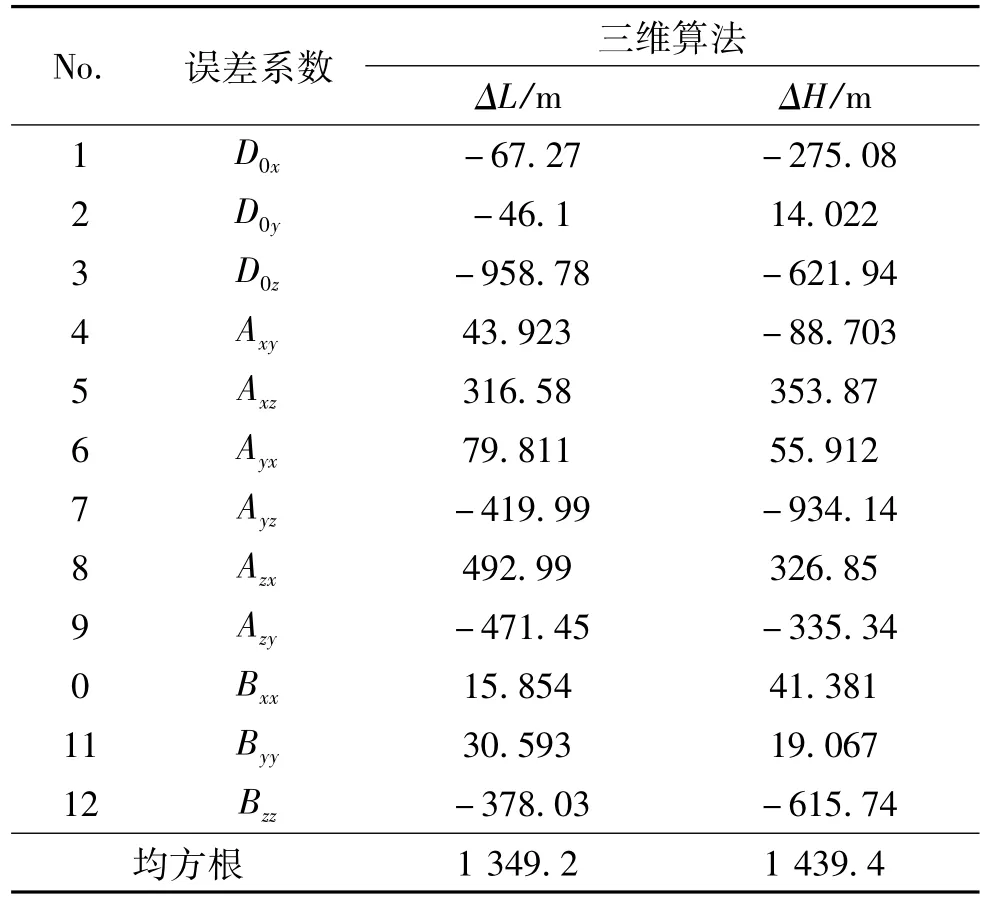
表3 基于三维算法全程惯组基准误差

表4 基于三维算法全程惯组测速误差

4 结论

针对基于常规弹道惯组累积误差计算方法中存在的过度简化等不足，提出利用弹道求差的思路进行三维制导误差计算的方法，实现了对机动弹道所产生的侧向视加速度、滚转与偏航角速度与相应惯组误差模型系数项相互作用结果的准确估计;利用某飞行器再入段无机动弹道数据进行了传统一维算法与三维算法计算结果的比对，一方面校核了新方法的正确性，另一方面也恢复了传统算法在计算加速度计测速误差过程中的忽略项。对全程机动的飞行过程进行惯组累积误差的计算结果说明，该三维算法具有一定的工程实用价值。

［1］Moses P L，Rausch V Z，Ngugen L T，et al.NASA hypersonic flight demonstrators:Overview，status and future plans［J］.Acta Astronautica，2004，55(3－ 9):619-630.

［2］徐延万.控制系统［M］.北京:中国宇航出版社，2009:384-424.

［3］徐军辉，郑玉航，汪立新，等.提高捷联惯组使用精度的方法研究［J］.宇航学报，2010，31(2):404-409.

［4］李刚，鲜勇.纯惯导中制导误差分析［J］.飞行力学，2007，25(2):50-52.

［5］杨希祥，张为华.速率捷联惯导系统工具误差计算与补偿研究［J］.弹箭与制导学报，2009，29(6):1-5.