小天体自主附着多滑模面鲁棒制导方法研究

袁旭,朱圣英,崔平远

(1.北京理工大学深空探测技术研究所,北京100081;2.飞行器动力学与控制教育部重点实验室,北京100081)

小天体自主附着多滑模面鲁棒制导方法研究

袁旭1,2,朱圣英1,2,崔平远1,2

(1.北京理工大学深空探测技术研究所,北京100081;2.飞行器动力学与控制教育部重点实验室,北京100081)

小天体形状不规则及缺乏观测信息的特点使得小天体附近的动力学环境较为复杂,附着动力学模型存在较大不确定性。通过引入多滑模面鲁棒制导方法,分别设计2个滑模面,使探测器状态先后到达这2个滑模面,可实现指定时刻精确附着小天体的目标。通过选取参数的分析总结了制导律中相关参数的选取对燃料消耗的影响,给出了制导律相关参数选取原则。在存在外界环境扰动、初始状态误差和导航误差条件下,蒙特卡洛仿真结果表明:多滑面制导方法能够在小天体的不确知环境中实现高精度附着,且具有很好的鲁棒性。多滑模面制导方法精度高、鲁棒性好,且无需设计参考轨迹,实时性好,适合小天体自主精确附着的任务需求。

小天体;自主附着;多滑模面制导;鲁棒性;参数选取

0 引 言

小天体探测是人们认识和研究太阳系起源与演化的重要手段,是21世纪深空探测活动的重要内容。随着小天体探测活动的不断发展,探测形式从飞越探测等简单形式逐渐向撞击、附着和采样返回等更为复杂;科学成果更加丰富的形式转变[1]。迄今,人类已成功地完成了3次小天体表面附着任务,分别为:2001年2月,NASA发射的NEAR探测器成功附着于433 Eros小行星,实现了首次小天体附着探测[2];2005年11月,日本JAXA发射的Hayabusa探测器附着于25143 Itokawa小行星并采样返回[3];欧洲空间局(ESA)发射的Rosetta探测器于2014年11月在67P/Churyumov-Gerasimenko彗星表面附着,实现了彗星表面的首次附着探测[4]。

由于小天体形状极不规则,小天体附近的动力学环境非常复杂,难以建立精确的动力学模型且弱引力环境下太阳光压等空间扰动的影响较大。所以在这种复杂不确定环境下,小天体附着制导控制方法需要具有良好的鲁棒性。滑模控制是一种重要的鲁棒控制方法,能够在系统具有模型不确定性且存在未知干扰的情况下达到控制的目标。Harl等(2004)首先在再入飞行器返回末端制导中应用了高阶滑模控制方法[5],此后多滑模面制导方法被引入到行星际着陆研究领域[6-7]。本文利用多滑面控制方法设计小天体自主附着制导律,通过设计2个滑模面并使探测器状态先后到达这2个滑模面,在指定时间精确附着的目标。

文章首先建立小天体附着问题的动力学模型;然后基于多滑面控制方法设计多滑模面鲁棒制导律并给出相应的稳定性分析;最后以433 Eros小行星为目标小天体进行蒙特卡洛仿真,验证制导方法的有效性和鲁棒性,并分析制导律中相关参数的选取对燃料消耗的影响,给出这些参数的选取原则。多滑模面制导方法在实现精确附着的前提下,算法简单,灵活性强,无需提前设计参考轨迹,并且具有良好的鲁棒性。

1 动力学模型

小天体固联坐标系内探测器的附着动力学方程为

设预定附着时间为tf,目标附着点为r(tf)=rd,且软着陆的末端速度需为零,即,初始时刻探测器的位置、速度分别为r(t0)=r0,v(t0)=v0.

2 滑模面与制导律设计

多滑模面制导方法通过设计2个滑模面来达到在指定时间精确附着的目标。在制导指令的导引下,探测器状态首先在有限时间内到达滑模面s2,然后沿着s2运动,这将保证探测器状态在预设的附着时刻到达滑模面s1,从而使探测器在该时刻到达目标附着位置,同时三轴速度均为零。

首先设计滑模面s1

其导数为

要实现定时定点软着陆,即要满足

若满足以下条件

其中:Λ=diag[Λ1Λ2Λ3],元素均为正实数,则设李雅普诺夫函数

于是李雅普诺夫函数稳定。事实上,系统状态不但可以到达滑模面,而且可保证在预定的tf时刻到达。式(4)可写为

当t→tf探测器将在预定时刻实现定点附着。于是只要设计制导律使式(4)得以满足,则设计滑模面

其中:Φ=diag{ϕ1ϕ2ϕ3},元素均为正实数。李雅普诺夫函数

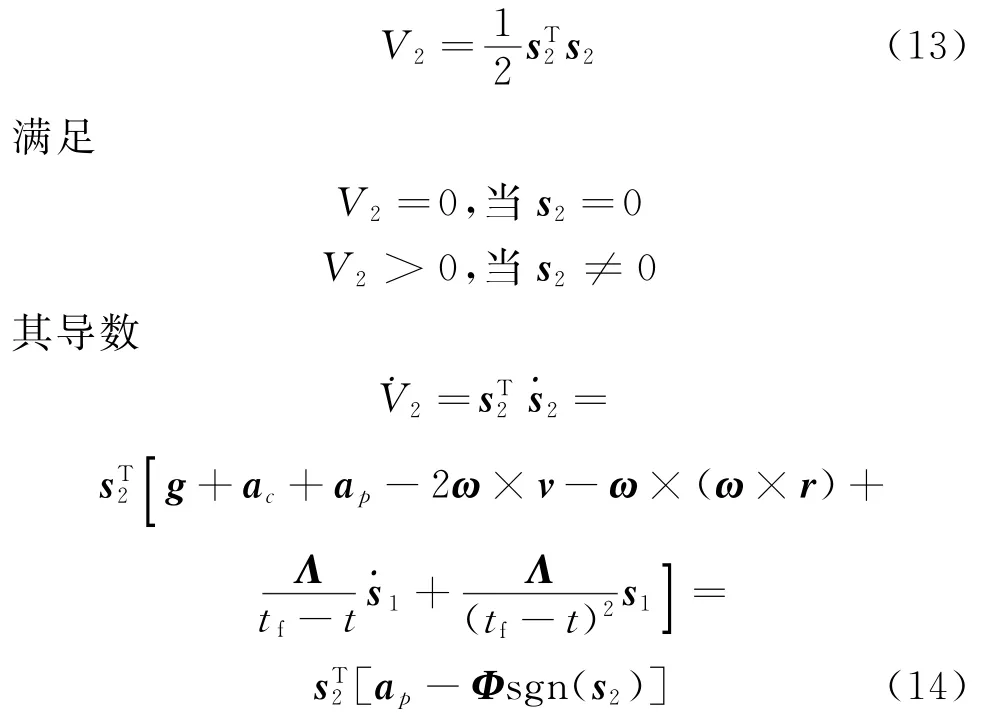
于是只要干扰加速度有上界,且反馈增益满足

即满足

李雅普诺夫函数稳定。

考虑到滑模控制方法普遍存在的系统到达滑模面附近后控制输入的抖阵问题,以饱和函数替代制导律中的符号函数,即

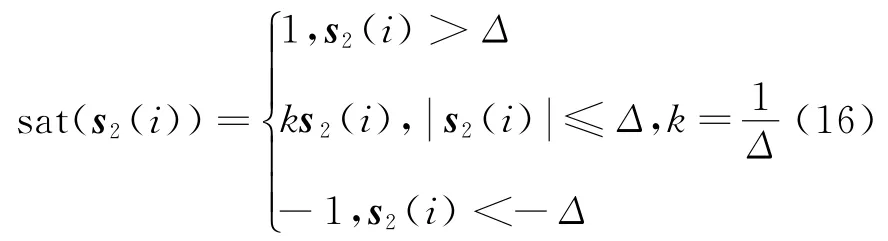
于是制导律化为

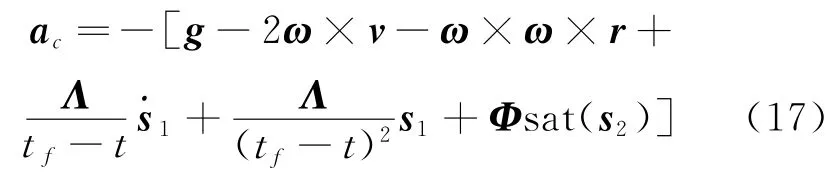
此制导规律不但可在存在模型不确定性和外界干扰的情况下实现精确附着,而且可消除抖振现象。虽然采用饱和函数替代符号函数会牺牲一定精度,但可控制在任务允许的精度范围内。

3 仿真验证与分析

3.1 仿真验证与蒙特卡洛分析

本节以附着433 Eros小行星为例进行仿真验证多滑面制导方法的有效性。Eros小行星自转角速度为ω=1 639.388 85(°)/d,引力常数μ=446 210 m3/s2[8];初始与目标位置、速度如表1所示;制导算法中Λ的对角线元素取值为λ1=λ2=λ3=2;tf=3 000 s。

仿真结果如图1～图5所示,其中图1、图2为探测器三轴位置和速度曲线,图3、图4分别为2个滑模面随时间变化曲线,图5为制导律给出的三轴控制加速度曲线。可以看到,在tf时刻,探测器到达目标位置,三轴速度控制为零值,符合软着陆条件;制导律中的2个滑模面均趋近并保持在零值附近,其中滑模面s1恰好在tf时刻到达零值,使探测器实现定时定点精确附着。

表1 仿真采用的初始与目标状态Table 1 Initial and final states in the simulations

图1 探测器三轴位置曲线Fig.1 Spacecraft position curves

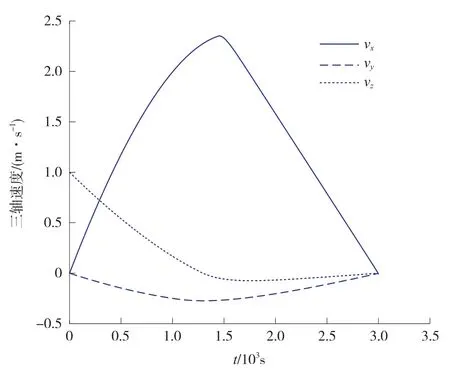
图2 探测器三轴速度曲线Fig.2 Spacecraft velocity curves

图3 滑模面s1曲线Fig.3 Sliding mode surface s1curves

为检验多滑面制导方法在小天体附近不确知环境中的制导性能,仍以附着433 Eros小行星为背景,在存在未建模干扰力、初始状态和导航误差的情况下,进行蒙特卡洛仿真分析。初始与目标位置、速度如表1所示;制导算法中Λ的对角线元素取值为λ1=λ2=λ3=2,tf=3 000 s。仿真中采用的初始位置误差为50 m/s,初始速度误差为0.5 m/s;导航误差为位置误差0.5 m,速度误差0.1 m/s;考虑的摄动力包括太阳光压和引力偏差两部分,其中太阳光压所致的扰动加速度在x轴与y轴方向分别呈均值为1×10-5m/s2,标准差为1×10-6m/s2的正态分布,引力加速度呈以其名义值为均值,名义值的10%为标准差的正态分布。仿真次数为500次。

表2列出了附着时刻y-z平面内的误差均值与标准差。图6为500次仿真的三维附着轨迹图,图7为y-z平面内的附着点位置及相应的σ散布椭圆。从仿真结果可见,多滑面制导律能够在存在未建模摄动、动力学模型不确定性、初始误差和导航误差的情况下导引探测器在目标位置实现定时定点精确附着,具有良好的精度和鲁棒性。

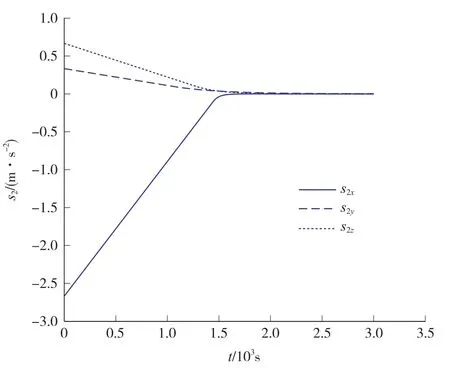
图4 滑模面s2曲线Fig.4 Sliding mode surface s2curves

图5 探测器三轴控制加速度曲线Fig.5 Spacecraft control acceleration curves

表2 y-z平面内的误差分布情况Table 2 Error distribution in y-z plane

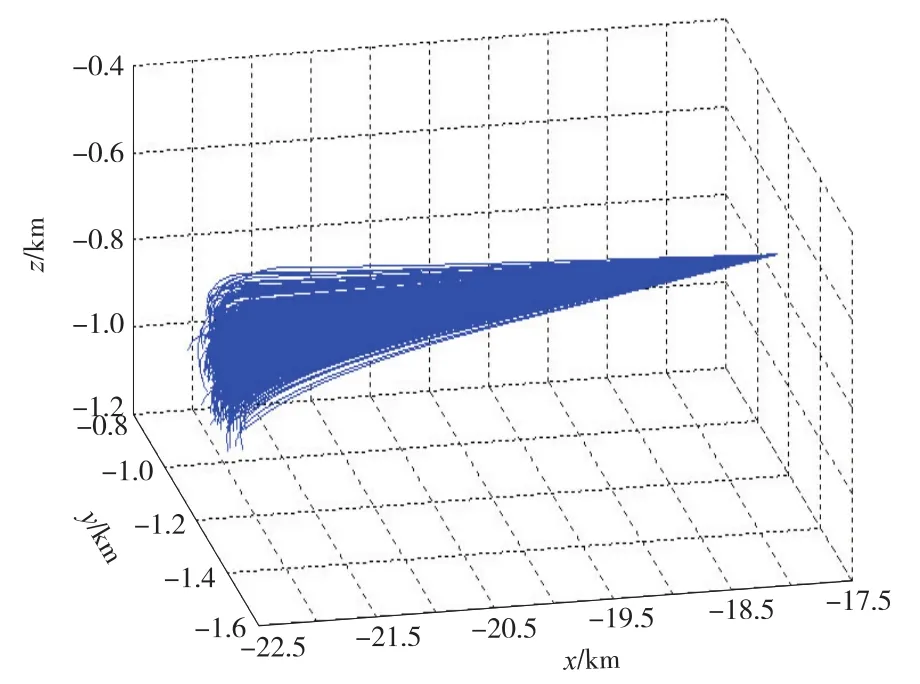
图6 三维附着轨迹图Fig.6 3D landing trajectory

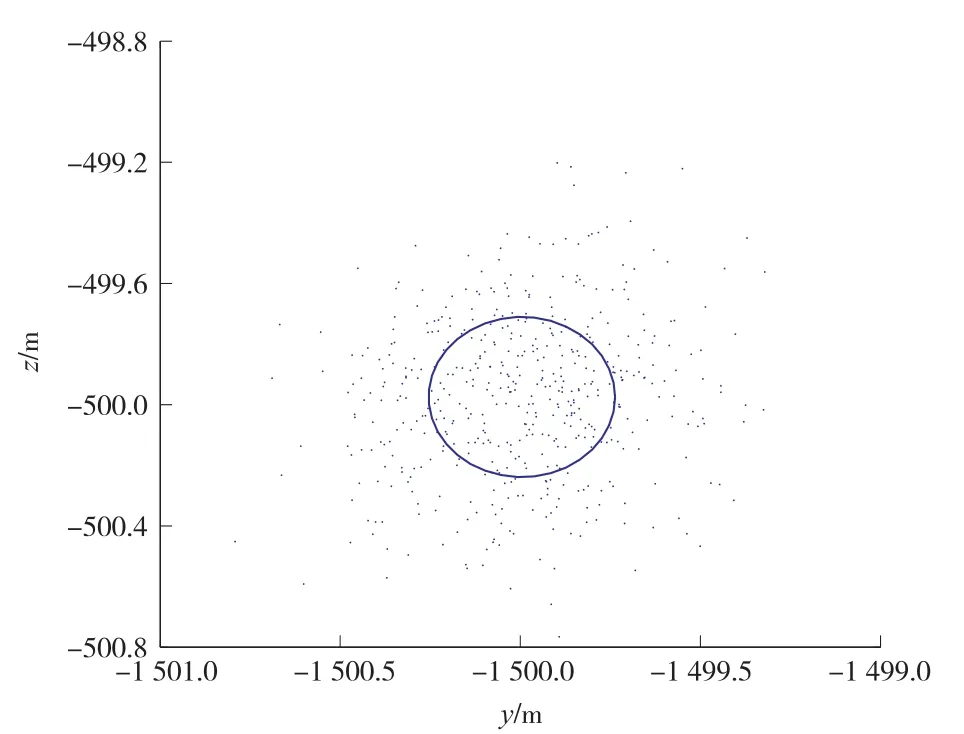
图7 y-z平面内的附着点位置Fig.7 Landing positions in y-z plane

3.2 参数选取对燃料消耗的影响

在具有良好的制导精度及对不确知环境的鲁棒性前提下,附着过程的燃料消耗也是重要的考量指标。制导律中参数的选取对附着过程的燃料消耗有直接的影响,为考察多滑模面制导律中相关参数对燃耗的影响,对滑模面s2中Λ的对角线元素λ和附着时间tf选择多组取值进行分析,并与开环的燃耗最优附着结果进行比较。

开环的燃耗最优附着轨迹利用高斯伪谱法求得[9]。考虑附着的初始和末端状态约束,以探测器到达目标附着点时的质量最大,即燃耗最少为优化目标,数学表达式为J=-m(tf)。仍以附着433 Eros小行星为背景,仿真的初始和目标位置、速度与3.1中相同,探测器初始质量为m=500 kg,发动机比冲为Isp=170 s,地球海平面重力加速度取g0=9.806 65 m/s2。制导律中λ与tf的取值如表3所示。其中tf=6 540 s为高斯伪谱法求得的开环燃耗最优轨迹的下降时间,最优的燃料消耗为1.17 kg。

表3 制导律中相关参数的不同取值Table 3 Different groups of parameter values in the guidance law

表4给出了这些参数的不同取值下附着过程的燃料消耗。可以看到,当附着时间tf固定时,燃料消耗随参数λ的增大而增大,在取最小值2时与开环最优燃耗最为接近。图8～图10显示λ越大,制导律给出的控制加速度指令越大,在使得探测器的速度和位置更快速地向目标值变化的同时,也使得燃料消耗增大。

图8 tf固定,λ取值不同时的x轴位置曲线Fig.8 Position curves in x axis(tffixed,λvaried)

当参数λ固定时,附着时间tf取不同值时,而tf取值与开环最优轨迹的下降时间一致时燃料消耗最小,当tf增大或减小时燃耗均增大,整个仿真在tf取6 450 s,λ取2时取得燃耗的最小值,为1.89 kg,与开环最优值接近。图11～图13显示,当tf较小时,制导律给出的控制加速度较大,以使探测器更快到达目标状态,相应地燃耗较多,且探测器速度较大;当tf大于开环最优值的下降时间时,虽然控制加速度较小,但时间的积累使得燃料消耗增多。

图9 tf固定,λ取值不同时的x轴速度曲线Fig.9 Velocity curves in x axis(tffixed,λvaried)

图10 tf固定,λ取值不同时的x轴控制加速度曲线Fig.10 Control curves in x axis(tffixed,λvaried)

表4 不同参数取值下的燃料消耗Table 4 Fuel consumptions corresponding to different groups of parameter values kg

以上结果与分析表明:附着的燃料消耗与制导律参数有关,为降低燃耗并使探测器平稳下降,制导参数λ设置不宜过高;在时间约束允许的情况下,应使下降时间尽量接近开环燃耗最优值,并适当选取其他制导参数,能够在保障精度与鲁棒性的同时达到接近最优的燃耗性能。

图11 λ固定,tf取值不同时的x轴位置曲线Fig.11 Position curves in x axis(λfixed,tfvaried)

图12 λ固定,tf取值不同时的x轴速度曲线Fig.12 Velocity curves in x axis(λfixed,tfvaried)

图13 λ固定,tf取值不同时的x轴控制加速度曲线Fig.13 Control curves in x axis(λfixed,tfvaried)

4 结 论

本文针对小天体附着探测,基于滑模控制方法设计了小天体自主附着多滑模面鲁棒制导方法。通过设计2个滑模面,并使2滑模面先后达到零值,达到在预定时间实现精确附着的目的,并给出了相应的稳定性证明。蒙特卡洛仿真分析表明:多滑面制导方法具有良好的精度和鲁棒性,在多干扰和导航误差等存在的条件下,仍能实现高精度附着,适合于小天体附着的多扰动、不确知环境。最后,分析了制导律参数选取对燃料消耗的影响,给出了制导参数的选取原则。

[1]崔平远,乔栋.小天体附近轨道动力学与控制研究现状与展望[J].力学进展,2013,43(5):526 539.[Cui P Y,Qiao D.Research progress and prospect of orbital dynamics and control near small bodies[J].Advances in Mechanics,2013,43(5):526-539.]

[2]Dunham D W,Farquhar R W,Mcadams J V,et al.Implementation of the first asteroid landing[J].Icarus,2002,159(2):433-438.

[3]Uo M,Shirakawa K,Hashimoto T,et al.Hayabusa’s touching-down to Itokawa-Autonomous guidance and navigation[J].The Journal of Space Technology and Science,2006,22(1):41.

[4]Hand E.Philae probe makes bumpy touchdown on a comet[J].Science,2014,346(6212):900-901.

[5]Harl N,Balakrishnan S N.Reentry terminal guidance through sliding mode control[J].Journal of Guidance,Control,and Dynamics,2010,33(1):186-199.

[6]Furfaro R,Wibben D R.Mars atmospheric entry guidance via multiple sliding surface guidance for reference trajectory tracking[C]∥AIAAAAS Astrodynamics Specialist Conference.[S.l]:AIAA,2012,4435:1-16.

[7]Furfaro R,Cersosimo D,Wibben D R.Asteroid precision landing via multiple sliding surfaces guidance techniques[J].Journal of Guidance,Control,and Dynamics,2013,36(4):1075-1092.

[8]Miller J K,Konopliv A S,Antreasian P G,et al.Determination of shape,gravity,and rotational state of asteroid 433 Eros[J].Icarus,2002,155(1):3-17.

[9]Wang H,Xie M,Zhang P,et al.Research of asteroid landing trajectory optimization based on gauss pseudo-spectral method[C]∥Intelligent Human-Machine Systems and Cybernetics(IHMSC),2014 Sixth International Conference.[S.l]:IEEE,2014,2:26-29.

作者简介:

袁旭(1986—),男,博士研究生,主要研究方向:深空探测器自主导航与控制。

通信地址:北京理工大学宇航学院22信箱(100081)电话:(010)68918910

E-mail:yuanxu@bit.edu.cn

Study on Robust Multiple Sliding Surface Guidance Method for Autonomous Small Celestial Body Landing

YUAN Xu1,2,ZHU Shengying1,2,CUI Pingyuan1,2
(1.School of Aerospace Engineering,Beijing Institute of Technology,Beijing 100081,China;2.Key Laboratory of Dynamics and Control of Flight Vehicle Ministry of Education,Beijing 100081,China)

The irregularity of small celestial bodies and lack of observation data make the dynamical environment around them complicated,thus the landing dynamic model has relatively large uncertainty.Using robust multiple sliding surface guidance method that derives two sliding surfaces and makes the state of the lander reach the surfaces successively can achieve the goal of precise small celestial body landing.The impact of the guidance parameters on fuel consumption is shown through parameter analysis,and principles of parameterselection for the guidance law are given.Monte Carlo simulations considering external environment perturbations,initial state errors and navigation errors show that the multiple sliding surface guidance method can achieve precision landing in the uncertain environment of a small celestial body,demonstrating robustness.The multiple sliding surface guidance method has high precision and fine robustness,needs no reference trajectory,demonstrates good real-time performance,and thus matches the requirement of autonomous precision small celestial body landing.

small celestial body;autonomous landing;multiple sliding surface guidance;robustness;reference selection

V448.233

A

2095-7777(2015)04-0345-07

10.15982/j.issn.2095-7777.2015.04.008

[责任编辑:宋宏]

2015-09-10

2015-10-18

国家重点基础研究发展计划(973项目)(2012CB720000);国家自然科学基金资助项目(61374216,61304226,61304248);教育部博士点基金资助项目(20121101120006)