基于对数势函数的深空探测器姿态规划与控制方法

武长青,徐瑞,朱圣英

(北京理工大学宇航学院,北京100081)

基于对数势函数的深空探测器姿态规划与控制方法

武长青,徐瑞,朱圣英

(北京理工大学宇航学院,北京100081)

针对深空探测器姿态约束机动问题,提出一种基于对数势函数的多约束姿态机动规划方法。首先,定义了两种姿态指向约束,即禁止约束和强制约束,并利用禁止约束和强制约束的性质构建了对数势函数作为Lyapunov函数;在此基础上采用改进退步法设计了探测器姿态机动控制器。数值仿真结果表明:该方法不仅在多约束情况下能够自主求出安全的机动路径,而且在分析和求解上计算效率较快,对于星上资源有限的深空探测器具有实际运用价值。

深空探测器;姿态规划;对数势函数;改进退步法

0 引 言

多约束下的姿态机动问题是深空探测器关键技术之一,探测器在进行科学任务过程中星上载荷发挥了巨大作用,但是这些载荷是脆弱的,他们容易受到强光强热天体的影响而导致失效,这对于深空探测任务是绝对要避免的。因此,规划出一条可行的姿态机动路径是格外的重要。与此同时,由于探测器约束机动的可行空间是非凸的[1],这对于探测器制导,导航与控制系统的计算能力有了更高的要求。

无姿态约束的姿态机动问题已经被广泛研究,但是针对存在以上复杂姿态约束情况下的姿态机动问题的研究还是有限的。McInnes等(1994,2005,2009)在文献[2-5]中将姿态指向约束引入到势能函数的构造中,用Lypunov第2法得出控制输入表达式,计算效率相对较高,但该方法利用欧拉角来表示运动学和动力学约束,会产生奇异点,而且对于多约束的姿态机动问题不能求解;Frazzoli等(2001)[6]应用随机规划理论求解该问题,以较快的搜索方式规划出可行姿态路径,由于算法对星上计算资源要求较高,所以对于深空探测器实现较难;仲维国等(2007)[7]在Frazzoli工作的基础上将姿态约束映射到罗德里格空间中规划姿态路径,提高了规划速度,由于没有考虑姿态动力学,很难满足实际工程应用。郑重等(2013)[8]提出了一种基于高斯势函数的航天器安全姿态跟踪控制方法,针对无扰动和有扰动的情形对禁忌约束进行了规避。郭延宁等(2011)[9]根据禁止姿态的影响范围构造了一种势函数并结合反步法设计了航天器自主姿态机动控制器。但是以上势函数只是针对单轴指向受到禁忌约束而构造的,当多轴受到约束而且约束种类不同的情况下,以上势函数方法有一定局限性。对数势函数法是在传统势函数的基础上发展起来的一种求解全局最优问题的方法[10],该方法不仅可以求解多约束情况下的全局最优解,而且对于计算能力要求不高,对于深空探测器的多约束姿态机动问题是一条有效途径。

本文提出一种对数势函数的深空探测器多约束姿态机动规划方法。首先,定义了两种姿态指向约束,即禁止约束和强制约束;并利用禁止约束和强制约束的性质构建了对数势函数作为Lyapunov函数;在此基础上采用改进退步法设计了探测器姿态机动控制器;最后进行了数值仿真来验证方法有效性。

1 问题描述

本文以刚体探测器为研究对象,为了避免出现奇异情况,采用四元数形式来表示探测器姿态机动过程中需要满足的动力学和运动学约束

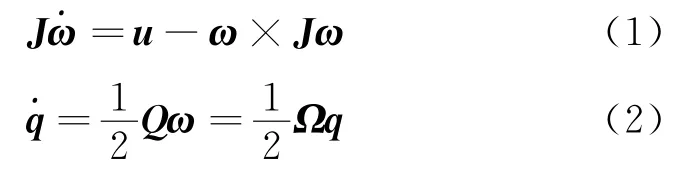
其中:姿态四元数q=[q0q1q2q3]T,它应当满足归一化要求表示2范数;角速度。且

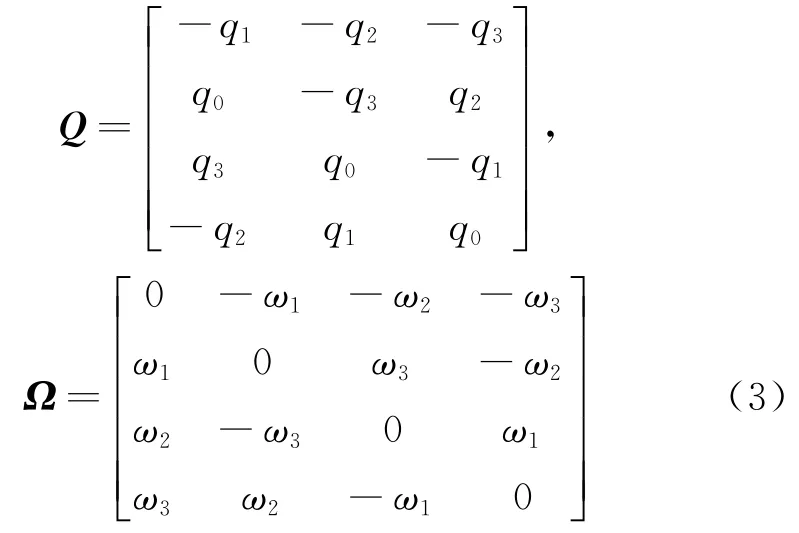
其中:J表示转动惯量;J=diag[J1J2J3];u表示控制力矩,u=[u1u2u3]T。

以上分析了探测器的动力学约束和运动学约束,只考虑这类约束问题可以从普通的姿态控制角度进行求解。但是值得注意的是探测器在进行深空探测任务是经常会遇到姿态指向约束。比如,在姿态机动过程中要避免强光天体(如太阳)进入某些光学敏感器(如:红外敏感元件或弱光敏感元件等)的视场内,否则将导致敏感元件的短暂致盲甚至损坏。同时,在整个机动过程中需要太阳电池阵方向矢量达到一定要求来满足能量供给。所以针对姿态指向约束我们有必要对其进行分析,而且我们更需要来研究和探讨如何能在计算资源有限的深空探测器上规划出姿态机动控制指令,在该指令驱使下探测器能规避所有这些复杂约束,安全地从初始状态机动到目标状态。

因此,在第3节针对姿态指向约束进行分类研究分析,并且为简化计算难度,把它表示成一种半正定二次型的形式。第4节利用禁止约束和强制约束的性质构建了对数势函数作为Lyapunov函数,在此基础上采用改进退步法设计了探测器姿态机动控制器。

2 姿态指向约束分析

探测器在执行空间任务时,会面临复杂的指向约束,这些约束缩小了姿态机动路径的可行空间。一旦指向约束不满足会对探测器携带的载荷造成严重的影响,进而影响任务的执行,所以对指向约束的分类和分析必不可少。姿态指向约束可以分为2类:禁忌约束和强制约束。

2.1 禁忌约束

在姿态机动过程中要避免强光天体(如太阳)进入某些光学敏感元件视场,以免损害敏感元件,这类约束称为禁忌约束。图1表示探测器姿态指向约束示意图,其中,rB表示某一光学敏感元件在本体坐标系下的方向矢量,rI表示某一强光天体在惯性系下的方向矢量。如果不让该强光天体进入光学敏感元件视场,也就是说要让rB和的夹角大于某个值θ,描述成数学表达式如下

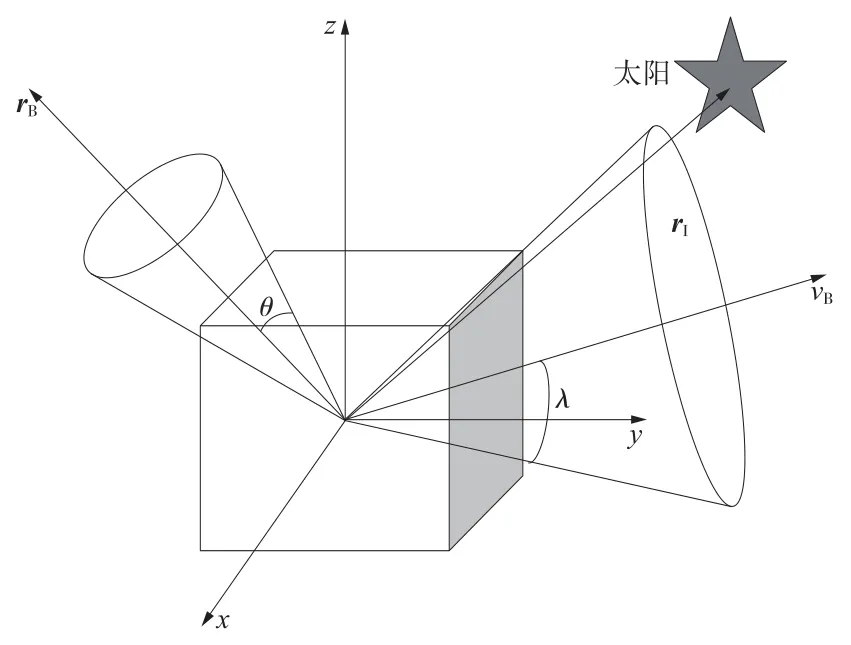
图1 探测器指向约束示意图Fig.1 Sketch map of explorer attitude point constraints

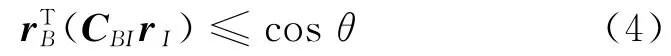
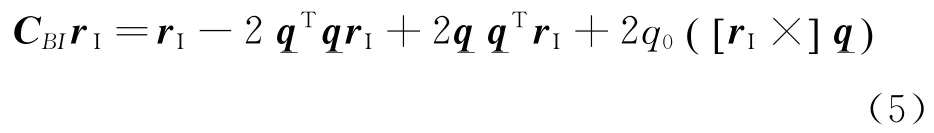
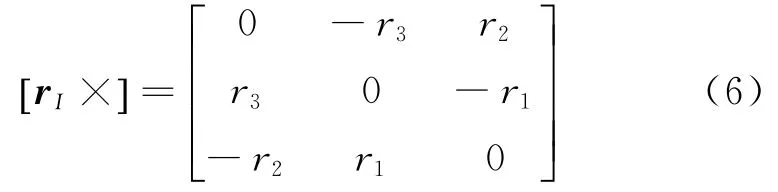
那么式(4)可以表示成更加简洁的二次型

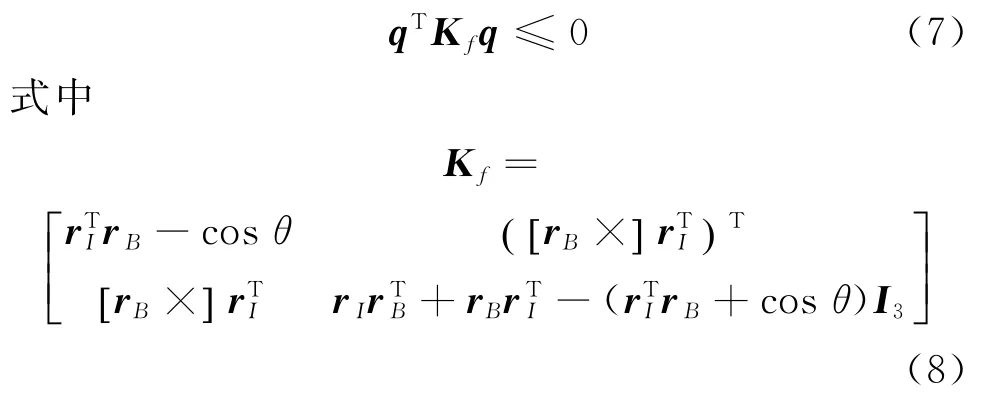
其中:[rB×]是rB的叉乘矩阵,表示方式同[rI×]。

2.2 强制约束

在空间任务中,探测器需要保持姿态在某一指向范围内,比如太阳能帆板要指向太阳,通信天线要指向地球等,这类指向约束称为强制约束。在图1中以太阳能帆板为例,vB表示太阳能帆板在本体坐标系下的方向矢量。要保持太阳能帆板指向太阳方向,也就是说vB和rI的夹角要小于某一值λ,即

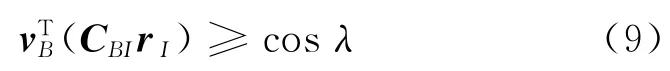
同理式转化成二次型

最终姿态指向约束表示成式(7)和式(10)形式,从式中可以看出该形式是半正定二次型形式,所以利用该形式来构建出渐进稳定的对数势函数,那么可以求出相应的控制率,该控制率驱使的姿态机动路径不仅是光滑的而且是全局最优的。

3 基于对数函数的控制器设计

第2节主要研究了探测器在姿态机动过程中所面临的指向约束,仅仅对于单轴受约束情况在文献[8-9]中已经进行了研究,但是每增加一个指向轴的约束,探测器的姿态可行空间很大程度地受到限制,对于问题的求解非常困难。因此本文首先考虑了一指向轴受到多禁忌约束,另一指向轴受到单强制约束的情况,这种情况在探测器姿态机动过程中是比较典型的,比如探测器在完成对科学目标进行成像的过程中,相机不仅要对准科学目标而且强光天体不能进入光学敏感器视场。因此本文引入了对数势函数方法,它不仅可以求解多约束情况下的全局最优解,而且对于计算能力要求不高。本文为了设计出满足指向约束的姿态机动路径,首先利用两类约束构建出以下姿态势函数,保证满足两类约束,而且要保证到达目标姿态

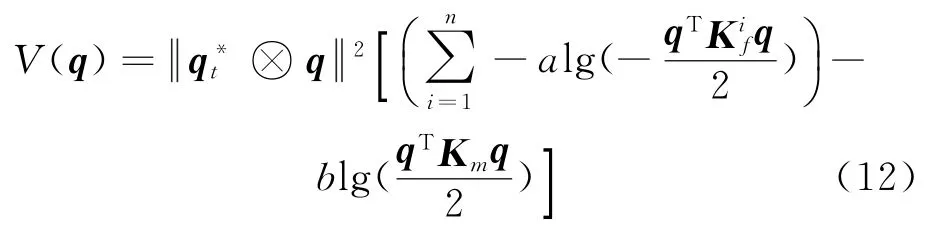
其中:a和b为正权衡常数;qt为目标姿态。

该对数势函数满足以下条件

1)V(qt)=0;

2)对于整个可行区域,V(q)＞0;

3)对于整个可行区域,▽2V(q)是正定的。

将该对数势函数选取为Lyapunov函数,然后考虑式(1)和式(2)动力学方程是级联结构,因此适合运用退步法来设计控制器。传统的退步法有个明显的缺陷是:在路径前部分控制信号会产生过度控制,而在后部分会产生响应缓慢。因此本文采用改进退步法来设计控制器[11]。

首先令

因此

因此对于该Lyapunov函数可以渐进收敛到目标姿态。而且,由式(2)可以得出虚拟控制输入角速度

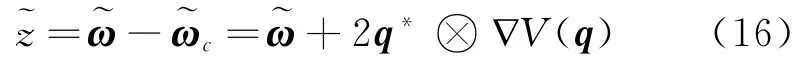
为了避免在路径前部分控制信号过度控制,令

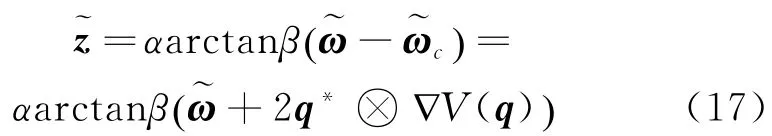
其中:α和β为形状参数[10]。因此可以得到关于的表达式

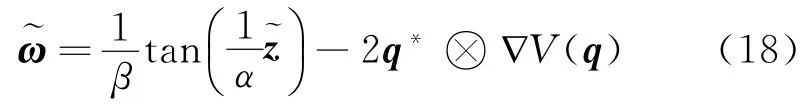
为了找到该系统的控制输入u(t),我们构建如下增广Lyapunov函数

对式(19)进行求导得

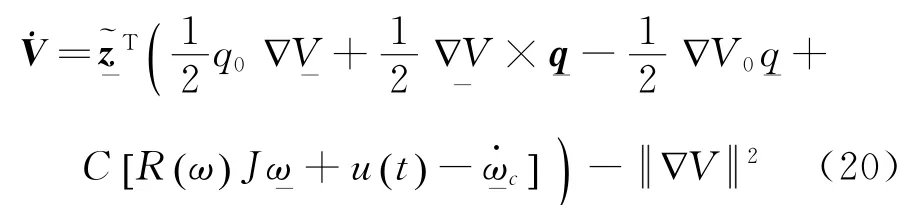
那么令

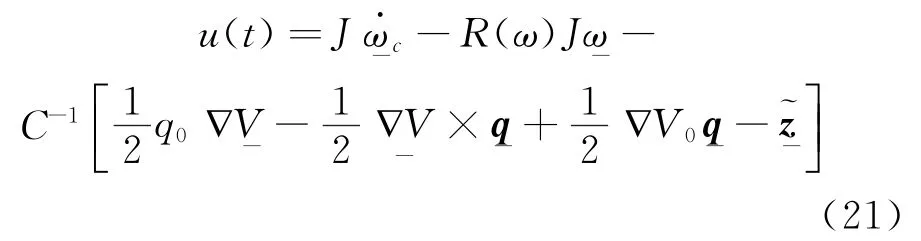
可得

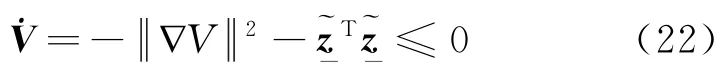
因此,按照式(21)的控制率可以实现探测器的约束姿态机动,最终可以得到一条安全有效的姿态机动路径。

4 数值仿真

在深空探测任务中,面临的指向约束通常只包括禁忌约束,4.1节中对存在3个禁忌约束的情况分别进行了仿真,没有考虑强制约束,但在某些特殊情况(比如太阳能帆板正在进行充电)下,两类指向约束耦合在一起,限制了姿态机动的可行域,造成一定难度。为了验证方法有效性,在4.2节中考虑了3个禁忌约束和1个强制约束。

4.1 只考虑禁忌约束情况下的仿真

在本小节中,假设航天器在[0 0 1]T方向安装了一个红外望远镜,在航天器姿态机动过程中红外望远镜需要规避有3个明亮天体,因此形成了3个禁忌约束。探测器的仿真参数如表1所示。

表1 仿真条件Table 1 Simulation conditions

利用本文提出的方法,对问题进行求解。图2为探测器天球坐标系下红外望远镜姿态机动路径,图3为探测器的姿态四元数时间历程曲线,图4为控制输入力矩时间历程曲线。从结果可以看出,姿态机动路径可以成功规避约束区域,实现从初始姿态到目标姿态的机动,而且角速度和控制输入都是有界的,避免了星上控制饱和问题。

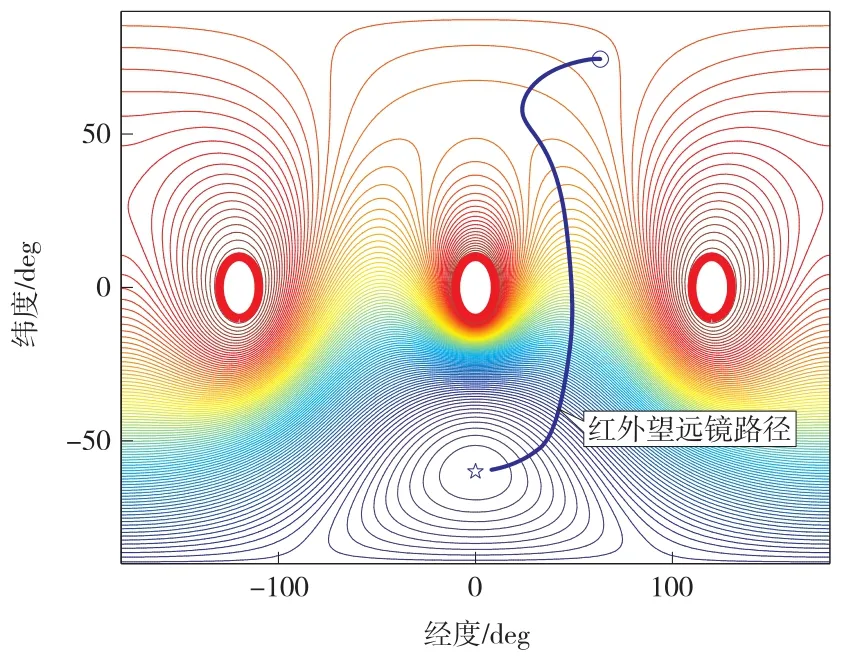
图2 探测器天球坐标系下红外望远镜姿态机动路径Fig.2 Attitude maneuver path of the telescope vector in the celestial coordinate system of explorer

图3 角速度时间历程曲线Fig.3 The time history of angular velocity

图4 控制力矩时间历程曲线Fig.4 The time history of control torque

4.2 同时考虑禁忌约束和强制约束下的仿真

大部分文献仅仅考虑了禁忌约束[2,5,12],没有考虑强制约束,但是在实际工程中,禁忌约束和强制约束往往会同时出现。文献[13]同时考虑了2类约束,但是其方法对星上计算效率要求较高,不适用于深空探测器。在本小节中,假设航天器在[0 0 1]T方向安装了一个红外望远镜,而且在[0 1 0]T方向安装了太阳能帆板。所以不仅要保证红外望远镜规避3个禁忌约束,而且要求太阳能帆板满足1个强制约束。其中第3个约束目标是太阳,对于红外望远镜是禁忌约束,而对于太阳能帆板是强制约束。更新后的仿真条件如表2所示。

表2 更新的仿真条件Table 2 Updated simulation conditions

图5表示了探测器天球坐标系下的红外望远镜和太阳能帆板的姿态机动路径,实线表示红外望远镜姿态机动路径,虚线表示太阳能帆板的姿态机动路径。值得注意的是,灰色区域对于红外望远镜是禁忌约束,在机动过程中需要规避,而对于太阳能帆板是强制约束,在机动过程中要在该区域内。从结果可以看出红外望远镜的姿态机动路径是安全的,而且太阳能帆板成功捕获太阳进行充能。

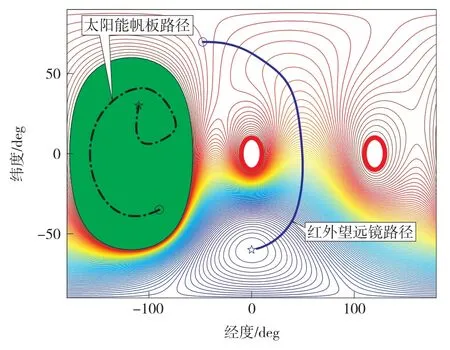
图5 探测器天球坐标系下红外望远镜和太阳能帆板姿态机动路径Fig.5 Attitude maneuver path of telescope vector and sun panel vector in the celestial coordinate system of explorer

图6和图7分别展示了探测器姿态机动过程中的角速度和控制力矩时间历程曲线。从图中可知,角速度以及控制力矩的有界约束得到很好的保证,均满足最大设定值的要求。而且本文方法在受到多约束耦合作用下,能够规划出的姿态机动路径不仅可以满足复杂的姿态约束。

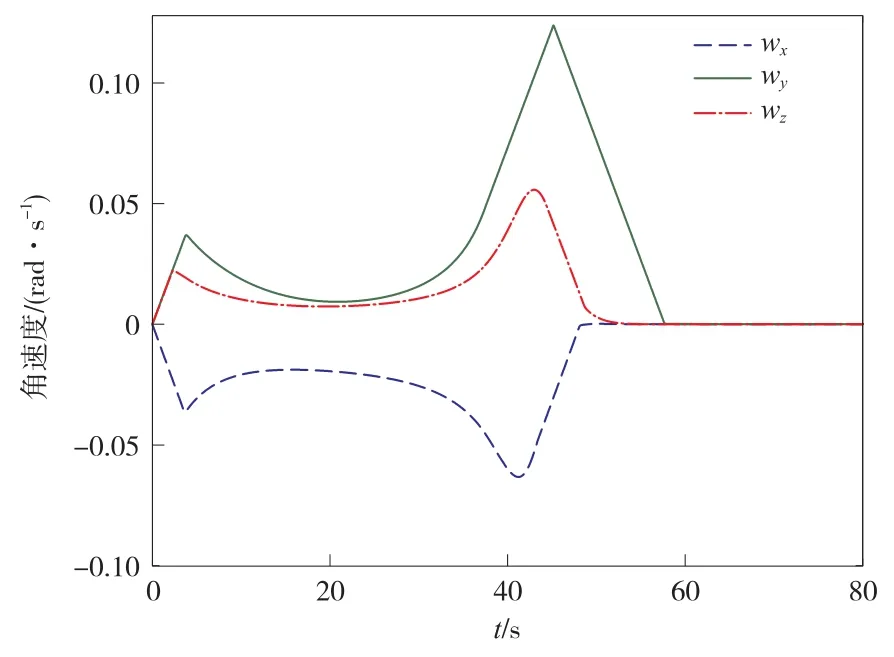
图6 角速度时间历程曲线Fig.6 The time history of angular velocity

图7 控制力矩时间历程曲线Fig.7 The time history of control torque

5 结 论

本文提出了一种基于对数势函数的深空探测器多约束姿态机动规划方法。首先,本文定义了2种姿态指向约束,即禁止约束和强制约束,并利用禁止约束和强制约束的性质构建了对数势函数作为Lyapunov函数。在此基础上采用改进退步法设计了探测器姿态机动控制器;最后进行了数值仿真验证,从结果可以看出,姿态机动路径可以成功规避约束区域,从而实现从初始姿态到目标姿态的机动。

[1]Kim Y,Mesbahi M,Singh G,et al.On the constrained attitude control problem[C]∥AIAA Guidance,Navigation,and Control Conference.[S.l.]:AIAA,2004,3:1862-1888.

[2]McInnes C R.Large-angle slew maneuvers with autonomous sun vector avoidance[J].Journal of Guidance,Control,and Dynamics,1994,17(4):875-877.

[3]Avanzini G,Radice G,Ali I.Potential approach for constrained autonomous manoeuvres of a spacecraft equipped with a cluster of control moment gyroscopes[J].Proceedings of the Institution of Mechanical Engineers,Part G:Journal of Aerospace Engineering,2009,223(3):285-296.

[4]Wisniewski R,Kulczycki P.Slew maneuver control for spacecraft equipped with star camera and reaction wheels[J].Control Engineering Practice,2005,13(3):349-356.

[5]Mengali G,Quarta A A.Spacecraft control with constrained fast reorientation and accurate pointing[J].The Aeronautical Journal,2004,108(1080):85-91

[6]Frazzoli E,Dahleh M A,Feron E,et al.A randomized attitude slew planning algorithm for autonomous spacecraft[C]∥AIAA Guidance,Navigation,and Control Conference and Exhibit.[S.l.]:AIAA,2001.

[7]仲维国,崔平远,崔祜涛.航天器复杂约束姿态机动的自主规划[J].航空学报,2007,25(5):1091-1097.[Zhong W G,Cui P Y,Cui H T.Autonomous attitude maneuver planning for spacecraft under complex constraints[J].Acta Aeronautica et Astronautica Sinica,2007,25(5):1091-1097.]

[8]郑重,宋申民,张保群.考虑姿态禁忌约束的航天器安全姿态跟踪控制[J].系统工程与电子技术,2013,35(3):574-579.[Zheng Z,Song S M,Zhang B Q.Spacecraft safe attitude tracking control by considering attitude forbidden constraint[J].Systems Engineering and E1ectronics,2013,35(3):574-579.]

[9]郭延宁,李传江,马广富.基于势函数法的航天器自主姿态机动控制[J].航空学报,2011,32(3):457-464.[Guo Y N,Li C J,Ma G F.Spacecraft autonomous attitude maneuver control by potential function method[J].Acta Aeronautica et Astronautica Sinica,2011,32(3):457-464.]

[10]Den H D,Roos C,Terlaky T.On the classical logarithmic barrier function method for a class of smooth convex programming problems[J].Journal of Optimization Theory and Applications,1992,73(1):1-25.

[11]Kim K,Kim Y.Robust backstepping control for slew maneuver using nonlinear tracking function[J].IEEE Control Systems Magazine,2003,11(6):822-829.

[12]Shuster M D.A survey of attituderepresentations[J].The Journal of the Astronautical Science,1993,41(4):439-517.[13]Sun C,Dai R.Spacecraft attitude control under constrained zones via quadratically constrained quadratic programming[C]∥AIAA Guidance,Navigation,and Control Conference.[S.l.]:AIAA,2015.

通信地址:北京理工大学宇航学院22信箱(100081)

电话:(010)68913550

E-mail:xurui@bit.edu.cn

Deep Space Explorer Attitude Planning and Control Method Based on Logarithmic Potential Function

WU Changqing,XU Rui,ZHU Shengying
(School of Aerospace Engineering,Beijing Institute of Technology,Beijing 100081,China)

A multi-constrained attitude maneuver planning method based on logarithmic potential function is proposed in this paper for attitude maneuver problem of deep space explorer.Firstly,two kinds of pointing constraints—forbidden constraint and mandatory constraint are defined,which are used to build alogarithmic potential function.This logarithmic potential function is chosen as the Lyapunov function.On this basis an attitude maneuver controller is designed via the improved back-stepping method.Numerical simulation results show that by this method,a safe attitude maneuver path could be autonomously planned out under complex constraints,and computational efficiency meets the requirements.So it has practical application for deep space explorer with limited resources.

deep space explorer;attitude planning;logarithmic potential function;improved backstepping method

V448.22+2

A

2095-7777(2015)04-0365-06

10.15982/j.issn.2095-7777.2015.04.011

徐瑞(1975—),男,副教授,主要研究方向:航天器姿态规划与控制。

[责任编辑:宋宏]

2015-09-25

2015-10-25

国家重点基础研究发展计划(973计划)(2012CB720000);国家自然科学基金(60803051);高等学校博士学科点专项科研基金(20111101110001);“十二五”民用航天预研项目