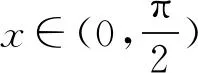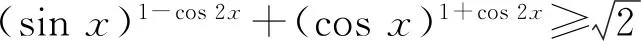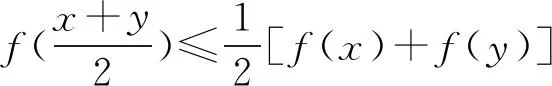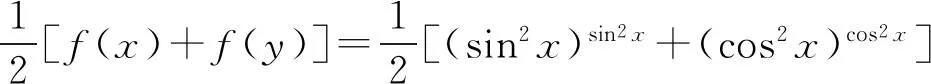凸函数的积分判别法及其应用
2015-12-09曹俊飞
曹俊飞
(广东第二师范学院 数学系,广东 广州 510310)
凸函数的积分判别法及其应用
曹俊飞
(广东第二师范学院 数学系,广东 广州 510310)
摘要:凸函数是一类非常重要的函数,有着广泛的应用,因此对凸函数的研究具有重要意义。本文首先建立了凸函数的积分判别法,并给出了此判别法与凸函数其他定义之间的等价关系。然后介绍了积分判别法中的Hadamard不等式,并证明了Hadamard不等式中等号成立的充分必要条件。最后举例说明了凸函数积分判别法的运用方法。
关键词:凸函数;积分判断法;Hadamard不等
中图分类号:O174
文献标志码:码:A
文章编号:号:2095-4824(2015)03-0098-05
收稿日期:2015-03-11
作者简介:曹俊飞(1982-),男,湖北黄冈人,广东第二师范学院数学系讲师,博士。
Abstract:Convex functions are a very important kind of functions which are been widely used in mathematical and other fields. Hence it is of great significance to study the judgment method of convex functions. First, this paper establishes the integral judgment method of convex functions and proves the equivalence between this theorem and other definitions of convex functions. Next it introduces the Hadamard inequality and proves the necessary and sufficient conditions for the medium-Hadamard inequality. Finally, several examples of the convex function application with the integral method are illustrated.
凸函数的定义最早是在1905年由Jensen给出的,自凸函数理论建立以来,凸函数这一重要概念已在许多数学分支中得到了非常广泛的应用。众多学者对凸函数的研究对其发展起着十分重要的作用。
作为数学中一个比较年轻的数学分支,凸函数是在上世纪50年代以后随着数学规划、最优化控制、数理经济学等应用数学学科的兴起而发展起来的[1]。到目前为止,凸函数的研究已经从凸函数的定义研究到更多的关于凸函数性质的研究以及凸函数性质的应用方面的研究。由于凸函数的理论的广泛性以及在数学各个领域的广泛应用,因此对凸函数理论进一步深入研究和推广显得尤为重要,对凸函数的判别、性质以及应用的研究具有十分重要的意义。
基于Jensen凸函数的定义和性质, 1893年Hadamard给出了经典的Hadamard不等式。Hadamard不等式是随着凸函数的发展而逐渐发转起来的,它是凸函数理论以及应用的重要组成部分。一直以来关于凸函数Hadamard不等式理论和应用的研究也一直是不等式和凸函数理论和应用研究的热点问题。
本文首先建立了凸函数的积分判别法,并给出了此判别法与凸函数其他定义之间的等价关系。然后介绍了积分判别法中的Hadamard不等式并证明Hadamard不等式中等号成立的充分必要条件。最后举例说明了凸函数积分判别法的应用实例。
1 预备知识
凸函数的定义最先是由Jensen所引入,定义如下:
定义1[2]若函数f(x)满足

(1)
则称f(x)为凸函数。
后来一些作者给出了如下的一般定义:
定义2[3]若函数f(x)满足
f(λx1+(1-λ)x2)≤λf(x1)+(1-λ)f(x2)
(2)
则称f(x)为凸函数。
注:若f(x)是区间I上的连续函数,则上述两个凸函数的原始定义是等价的[2]。
凸函数还有很多等价的定义:
定义3[2]如果对∀x1,x,x2∈I,x1 则称f为I内的凸函数。 则称f为I内的凸函数。 定义5[2]如果对∀x1,x2∈I,x1 则称f为I内的凸函数。 定义6[2]若函数f(x)满足 (1)∀x∈I,f′-(x),f′+(x)存在,且f′-(x)≤f′+(x); (2)∀x1,x2∈I,x1 则称f为I内的凸函数。 定义7[2]若果函数f(x)满足在I内存在单调增加的函数φ,∃x0∈I,∀x∈I, 则称f为I内的凸函数。 定义8[4]若对∀x1,x2,…,xn∈I,函数f(x)满足 则称f为I内的凸函数。 定义9[5]若函数f(x)满足在I内可导,且对∀x,y∈I,有 f(x)≥f′(y)(x-y)+f(y), 则称f为I内的凸函数。 定义10[6]设函数f(x)在I内连续,且二次可导,f″(x)≥0,则称f为I内的凸函数。 定义11[7]若对∀x1,x2∈I,函数f(x)满足 φ(λ)=f[λx1+(1-λ)x2],为[0,1]上的凸函数,则称f为I内的凸函数。 定义12[5]若函数f(x)满足在I内可导,且f′(x)单调递增,则称f为凸函数。 本节将建立凸函数的积分判别法。 定理1 若对任何a 则f为凸函数。 定理2 若对任何a 则f为凸函数。 注:上述两个积分不等式称为Hadamard不等式。 证明:(1) 证明第一条不等式: 令 x=x1+λ(x2-x1),λ∈(0,1) 则 同理,令 x=x2-λ(x2-x1),λ∈(0,1), 有 从而 综上可得: 与已知不等式 相矛盾。故可知f是凸函数。 (2) 证明第二个不等式: 令x=x1+λ(x2-x1),λ∈(0,1),则有: 假设f不是凸函数,则: f[x1+λ(x2-x1)]=f[λx2+(1-λ)x1]>λf(x2)+(1-λ)f(x1) 所以: 与已知不等式 上述两个积分不等式可以判断一个函数是不是凸函数,由此建立凸函数的积分判别法。通过建立积分判别法,使得函数在微积分学有了更加充分的作用。 命题1若函数f(x)满足在I上连续,则可以由定义11⟹定理1。 证明:对∀x1,x2∈I,由于 φ(λ)=f[λx1+(1-λ)x2]为[0,1]上的凸函数,所以: f[λx1+(1-λ)x2]=φ(λ)=φ·1+(1-λ)·0] ≤λφ(1)+(1-λ)φ(0)=λf(x1)+(1-λ)f(x2) 所以f为凸函数。 即得到 命题2若函数f(x)在I内可导,则可以由定义9⟹定理2. 证明:函数f在I内有定义,且f在I内可导,若f为I上的凸函数,则: 由定义9可知:∀x,y∈I,y f(x)≥f(y)+f′(y)(x-y), 则 而 又因为 所以 即 则 所以命题得证。 通过以上的证明可知,本文建立的凸函数积分判别法与已有的定义是等价的,从而说明本文建立的定理的正确性。 设函数f(x)是区间[a,b]上的凸函数,则对于a≤x1 仅当f为线性函数时等号成立,它说明在Jensen不等式的两端之间可以用积分的平均值插入[8]。由此得出以下两个性质: 定理3若函数f(x)在[a,b]内连续,且为区间上的凸函数,则: (3) 成立的充要条件是:在[a,b]上,有 (4) 证明:充分性:对(4)式两端从a到b积分, 所以: 必要性:因为f是凸函数,按照凸函数的定义3,可知 (5) 特别地,取x1=a,x2=b,则(5)可以化成: (6) 上式左边是连续函数,对其积分可以得到: 所以: 所以在[a,b]上, 必要性得证。 定理4若函数f(x)在[a,b]内连续,且为区间上的凸函数,则: (7) 的充要条件是:在[a,b]上,有 (8) (9) 对(8)式两端从a到b积分,可以得到: 所以可以得到: 可见充分性得证。 也就是说: 上式左边是连续函数,所以对其积分可得: 所以可以得到: 在上式中,取x=a,即可以得到: 同理:再对(6)式左边积分,得 所以: 所以在[a,b]上, 即必要性得证。 注:定理3连续的条件不能去掉。 证明:原不等式等价于: 设f(x)=xx,则由凸函数的积分判别法知f(x)为(0,∞)上的凸函数,故当x>0,y>0时, 令x=sin2x,y=cos2x,则: 例2a>0,b>0,n∈N+且n≠1,则有以下均值关系: 证明:设 f(x)=xn,x∈(0,+∞),f″(x)=n(n-1)xn-2>0, 所以f为凸函数。即对任意的正数有: 可以得到: 证毕。 [参考文献] [1]华东师范大学数学系.数学分析[M].北京:高等教育出版社,2010. [2]刘国华, 陈妍, 庞培林,等. 关于凸函数的八个等价定义[J]. 河北建筑科技学院学报:自然科学版, 2003, 20(3):82-83. [3]华东师范大学数学系,数学分析[M]. 北京:高等教育出版社, 1980. [4]俞文辉.凸函数不同定义间的关系及其应用[J]. 南昌高专学报, 2005, 60(5):112-113. [5]郭素霞.关于凸函数定义的讨论[J]. 衡水师专学报, 2000, 2(4):49-52. [6]尹传勇.凸函数的等价命题[J].中国高等教育论坛,1998,10(2):21-24. [7]钟伟, 周彬林. 凸函数的几种不同定义及作用[J]. 九江学院学报:哲学社会科学版, 2007, 26(3):74-77. [8]匡继昌. 常用不等式[M]. 3版.济南: 山东科学技术出版社, 2004. Integral Judgment Method of Convex Function and Its Applications Cao Junfei (DepartmentofMathematics,GuangdongUniversityofEducation,Guangzhou,Guangdong510310,China) Key Words:convex function;integral judgment method;Hadamard inequality (责任编辑:张凯兵)
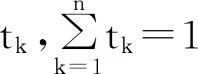
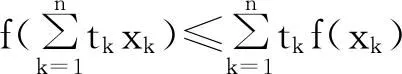
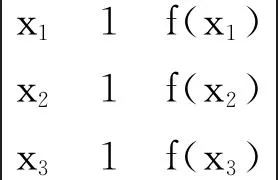


2 凸函数积分判别法

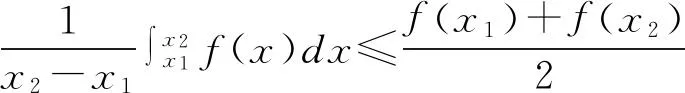
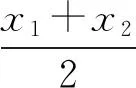

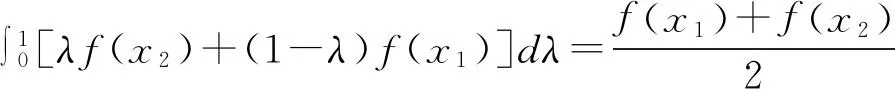
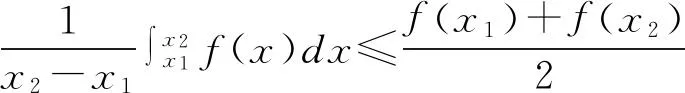
3 凸函数积分判别法与凸函数其他定义的关系

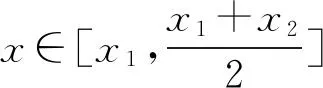
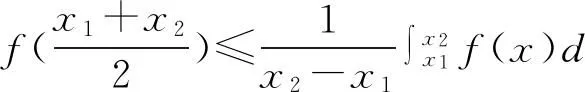

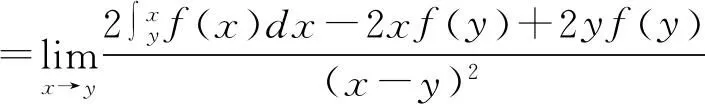

4 Hadamard不等式等号成立的充要条件



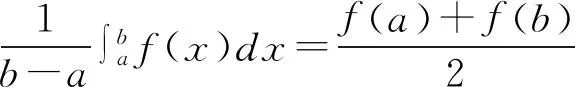


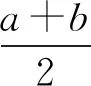

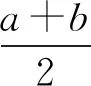


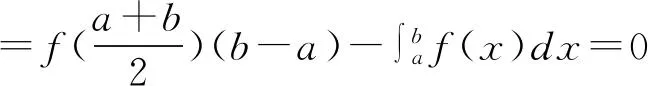
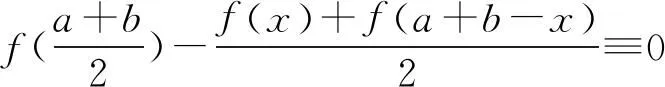
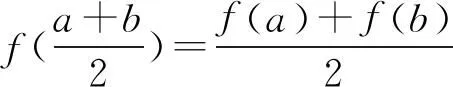
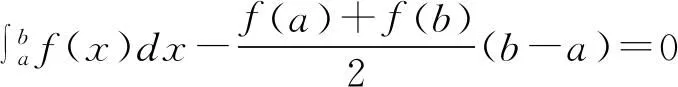
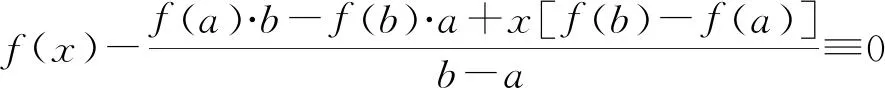

5 应用