两种聚类模型在城市垃圾清运路径规划中的应用

王　龙，刘世于，胡建波

(重庆交通大学 机电与汽车学院，重庆 404100)

两种聚类模型在城市垃圾清运路径规划中的应用

王龙，刘世于，胡建波

(重庆交通大学 机电与汽车学院，重庆 404100)

摘要:基于广东省深圳市南山区的实地调查，提出了一种新的城市垃圾处理设备的分布设计和清运方案。在厨余垃圾处理设备的分布设计时，建立了两种数学模型，即最短距离聚类模型和k-Means聚类模型。通过对两者的比较得出k-Means聚类模型更适合垃圾清运路径的规划。本文提出的方法对解决深圳市南山区垃圾处理的路径规划具有较高的准确性，可用于全国其他各大城市的垃圾处理方案设计中。

关键词：城市垃圾处理；最短距离聚类； k-Means聚类法；路径规划

中图分类号：O159

文献标志码：码：A

文章编号：号：2095-4824(2015)03-0026-06

收稿日期：2015-03-21

作者简介：王龙(1989-)，男，河南渑池人，重庆交通大学机电与汽车学院硕士研究生。

Abstract：Based on the fieldwork in Nanshan District, Shenzhen city, Guangdong province, this paper proposes a new distribution design for waste disposal equipments and removal programs. For achieving the distribution design for waste disposal equipments, two mathematical models, namely the shortest distance clustering model and k-Means clustering model are established. By comparing the two models, it is shown that the k-Means clustering method is more suitable to path planning for urban waste disposal. The proposed method shows more accurate for waste disposal in Nanshan District, Shenzhen city, and can be applied to the waste disposal program project in the major cities across the country.

刘世于(1990-)，男，黑龙江哈尔滨人，重庆交通大学机电与汽车学院硕士研究生。

胡建波(1989-)，男，四川遂宁人，重庆交通大学机电与汽车学院硕士研究生。

垃圾分类化收集与处理不仅有利于减少垃圾的产生，有益于环境保护，而且有利于资源回收与再利用，是一项重要的城市绿色工程。我国大城市，如北京、上海、重庆和深圳，已经开展了垃圾分类化处理，并且取得了一定成效，但垃圾分类化进程中仍然面临许多问题，其中垃圾处理设备的选址是非常关键的问题之一。合理地进行垃圾处理设备的选址，不仅可以减少垃圾处理设备的总费用，而且能减少垃圾的二次污染。垃圾站选址属于邻避型(不受欢迎型)设施选址问题[1]，需要综合考虑厨余设备本身处理垃圾的能力和如何尽量减少污染排放。

目前，国内外学者主要用线性优化建立多目标方程得出最优选址位置。如栗娜和李珍萍建立的垃圾站对居民的影响和垃圾站建设运营成本均极小化的双目标选址问题数学模型[2]；贾传兴等[3]选用集合覆盖模型对中转站的位置进行初步优化,确定了垃圾中转站的待选点。在此基础上,运用整数规划构建整个城市垃圾收运系统费用现值最小模型,对城市垃圾中转站的初步规划进行二次优化,从待选点中选出垃圾中转站的最优组合。另外还有一些学者用模糊综合评判方法进行垃圾站的选址。如刘云斌使用模糊综合评判系统进行城市生活垃圾填埋场选址[4]。然而，这些方法不能直接表达结果的优劣，更反映不出城市垃圾的聚集性和紧凑性，只是单纯用一些量化目标来对结果进行评价。鉴于此，本文采用聚类算法对城市垃圾清运路径规划问题进行研究，方法简单易用，并取得了较好的效果。

垃圾处理设备的选用问题取决于垃圾点的位置分布和垃圾数量，是一个非线性规划问题，无法建立精确的模型。因此，本文采用最短距离聚类模型和k-Means 聚类模型来确定大型厨余垃圾处理设备的数量，利用中位点选址优化模型和Matlab编程求解厨余垃圾处理设备的位置分布。对于垃圾清运路线的设计，本着效益最大化和路程最小化原则，采用k-Means聚类方法将垃圾转运站划分成若干个区域，然后利用TSP(Traveling Salesman Problem)模型和下山逐点搜索法确定垃圾的最优运输路线。

1　两种不同的聚类模型

深圳市南山区的垃圾分为厨余垃圾、可回收垃圾、有害垃圾和其他不可回收垃圾。城市垃圾将从各小区的垃圾站运往附近的垃圾转运站，在垃圾转运站进行分类后，厨余垃圾运往厨余垃圾处理中心，可回收垃圾在垃圾转运站进行分类再利用，有害垃圾和不可回收垃圾运往填埋场或垃圾焚烧厂处理。简而言之，南山区的垃圾的清运工作包括收集清运和中转清运两个阶段。收集清运使用60辆2.5吨的收集汽车将南山区中每个小区产生的垃圾运到各自临近的垃圾中转站；而中转清运使用16辆载重10吨的拖车将中转站已经分类好的垃圾转运到各自的处理中心。

1.1　最短距离聚类模型

1.1.1 模型表示

将把每一个转运站看成一类，依次记为G1，G2，…，G38，构造38个转运站间的距离矩阵D：

然后以距离矩阵D为基础，利用最短距离方法聚类。

最短距离聚类法是在原来的m×m距离矩阵的非对角元素中找出 ，把分类对象归并为一个新类，然后按比较后的最小距离来计算原来各类与新类之间的距离，这样就得到一个新的(m-1)阶的距离矩阵；再从新的距离矩阵中选出最小者，把两者归并成新类；再计算各类与新类的距离，这样一直下去，直至各分类对象被归并为一类为止。

1.1.2　最短距离聚类算法

最短距离聚类模型的算法流程如下[5]：

Step 1：在距离矩阵D的非对角元素中找出距离最短的两个类Gp和Gq，并为一新类Gr。

Step 2：然后按计算公式

(1)

计算原来各类与新类之间的距离，得到一个新的37阶的距离矩阵。

Step 3：转至Step 1，直到各分类对象被归为一类为止。

1.1.3　最短距离聚类模型求解

以所给卫星地图的直角坐标系，测出38个垃圾转运站的相对坐标，结果如表1。

表1 　垃圾转运站位置的相对坐标

基于以上分析和最短距离聚类算法流程，把38个垃圾转运站点划分为3类，聚类数量主要通过大、小型厨余垃圾的处理量和厨余垃圾总量进行划分。通过计算发现，厨余垃圾总量需要两个大型厨余设备和若干个小型厨余设备。考虑到经济性和合理性，且大型厨余设备污染更少，因此把38个站点划分成3类。具体做法是利用Matlab中的pdist函数和squareform函数将坐标转化为距离矩阵[6]，并利用linkage和cluster函数进行最短距离聚类，通过对最短距离聚类谱系图的绘制(见图1)，得到表2的分类结果。

表2　垃圾转运站分类结果

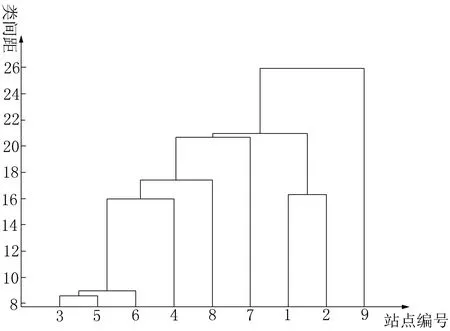
图1　最短距离聚类谱系图

根据表2，可以得出：一区建立92台小型设备；二区建立2台大型设备和8台小型设备；三区建立138台小型设备。在不考虑运费的情况下，计算出总费用为15 440万元

1.2　k-Means 聚类模型

1.2.1　k-Means 聚类基本思路

根据输入的聚类参数k，将事先输入的n个数据对象划分为 k个聚类，使得所获得的聚类满足如下条件：同一聚类中的对象相似度较高，而不同聚类中的对象相似度较小。聚类相似度利用各聚类中对象的均值进行计算的。

1.2.2 k-Means 聚类算法

k-Means 聚类算法的基本流程如下：

Step 2：对数据集中的每个样本点xi，计算其与各个聚类中心cj的欧式距离并获取其类别标号：

(2)

Step 3：按下式重新计算3聚类中心

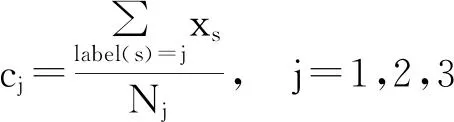
(3)

Step 4：重复Step 2和Step 3，直到达到最大迭代次数为止。

1.2.2 k-Means聚类模型求解

将测出的38个垃圾转运站的坐标值利用Matlab中的pdist函数和squareform函数将坐标转化为距离矩阵，并利用k-Means函数进行最短距离聚类[7]，聚类结果如表3所示。

表3　垃圾转运站的k-Means分类结果

根据k-Means分析结果，建议在一区建立一个大型设备；二区建立一个大型设备；三区建立一个大型设备和14个小型设备。在不考虑运费的情况下，计算出总费用为13 867万元。

1.3　两种聚类结果的比较

使用最短距离聚类得到的大型设备过于集中在二区，出现扎堆现象，分布不合理，容易导致二区的大型设备不能全力工作，而一区和三区小型设备太多，容易导致大量的污染，因而经济效益低下。使用k-Means聚类法得到的三个小区的设备在整体上分布比较平均，分类比较集中，各个小区分别配备一套大型设备，总体经济效益比最短距离聚类方法更好，污染更少。

通过对两种方案的比较，从两方面可以看出 k-Means聚类法的优点。

1)最短距离聚类仅仅将距离相近的多个地方划分同一类，缺乏整体的平均性，容易造成扎堆现象，无法使两个聚类群独立起来，类与类之间区别不明显，容易导致分类结果的不合理性。

2)k-Means聚类法采用迭代方法能使整个分布更紧凑，迭代次数越多，分类越集中，最终能得到紧凑且独立的簇，且同一聚类中的对象相似度较高。本算法确定的k 个划分到达平方误差最小。当聚类密集且类与类之间区别明显时，分类效果较好。对于大数据集，该算法具有相对较好的可伸缩和计算效率。

通过上述分析，最短聚类所得的规划结果总费用较多，因此本文建议采用k-Means聚类算法的结果作为最优方案。

2　中位点选址优化模型

根据垃圾转运站的最终聚类结果和厨余垃圾处理设备的分布设计，首先用高精地图测出每一个垃圾转运站vi至各个站点vj的最短路径长度dij(i，j = 1，2，…)，求出三类内部的距离矩阵：

(4)

然后建立模型确定每一类内部厨余垃圾处理中心的位置。

以距离和各转运站的厨余垃圾量乘积之和为运行成本，以成本值为目标函数确定垃圾处理设备的具体位置。考虑目标函数

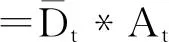
(5)

式中：At=[a(v1)，a(v2)…a(vn)]为每类中各站点的载荷矩阵(厨余垃圾量)。

以每一类内部为约束条件，以各垃圾转运站点的载荷加权，用Matlab中的矩阵运算求得每一个站点至各个站点的最短路径长度的加权和，最后得出3个大型厨余垃圾处理设备位置。表4是垃圾转运站最终聚类结果。

表4　垃圾转运站最终聚类结果

3　焚烧垃圾的清运路线

3.1　车辆分配模型求解

由于车辆有限，本文先将16辆车分给三类垃圾的运输，为此建立加权载荷模型求解垃圾站车辆的分配，模型如下：

(6)

式中：xij表示观测值；Dij表示观测值的对应权数；αi表示权算术平均数(即预测值)。运输厨余垃圾的拖车所占比率为：

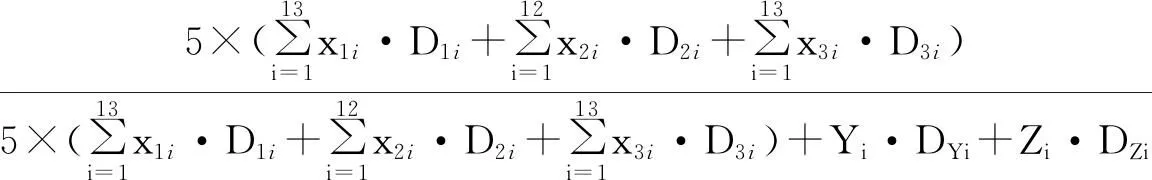
(7)

运输焚烧垃圾的拖车所占比率：

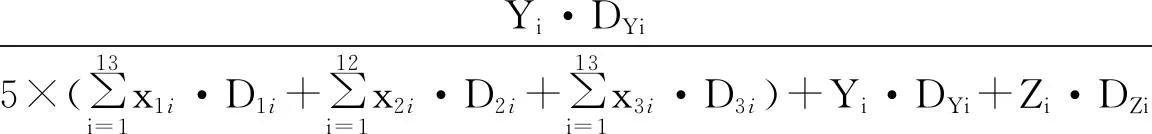
(8)

运输填埋垃圾的拖车所占比率：

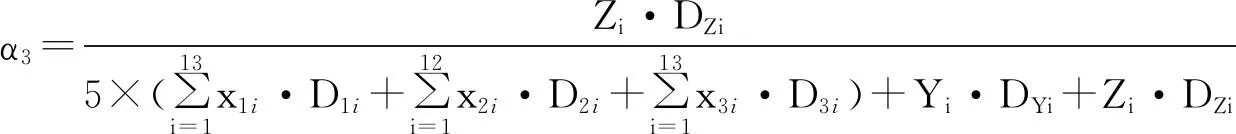
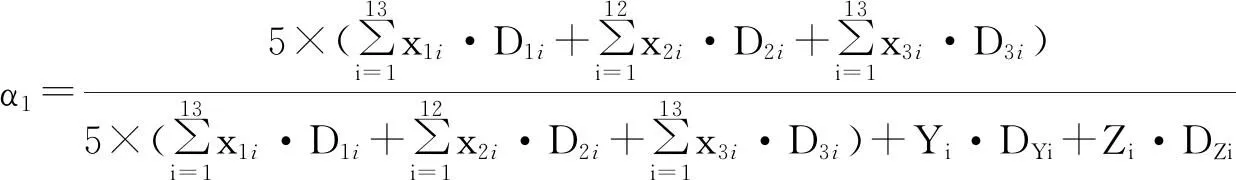
(7)

运输焚烧垃圾的拖车所占比率：

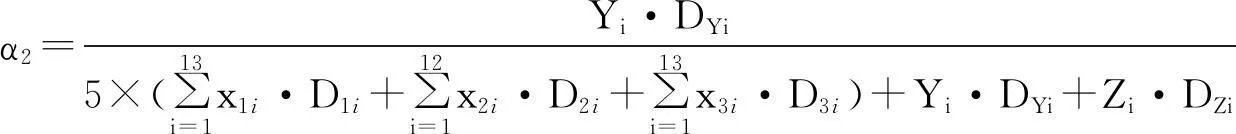
(8)

运输填埋垃圾的拖车所占比率：

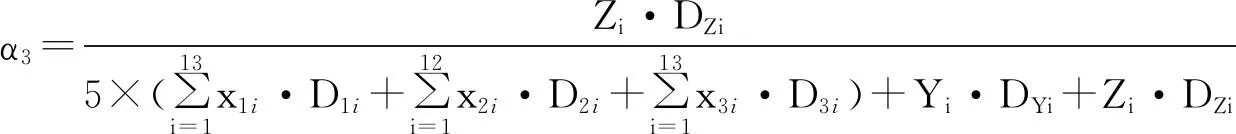
(9)

采用加权载荷法求解不同类型运输车辆的分配情况，结果如表5所示。

3.2　垃圾清运路径规划

TSP模型是路运输问题的最为典型的一个模型，它的全称是TravelingSalesman Problem(TSP)，中文称作旅行商问题[8]。TSP模型描述如下：在给出的一个顶点网络(有向或无向)，要求找出一个包含所有顶点的具有最小耗费环路。任何一个包含网络中所有n个顶点的环路被称作一个回路。在旅行商问题中，要设法找到一条最小耗费的回路。

表5　垃圾转运站车辆分配结果

TSP模型数学表达式如下：

∃连通图H，其顶点集合A，顶点间距离集为

(10)

目标函数：

(11)

约束条件为：

决策变量：

如果xij=0，从i到j无通路；如果xij=1，从i到j有通路。

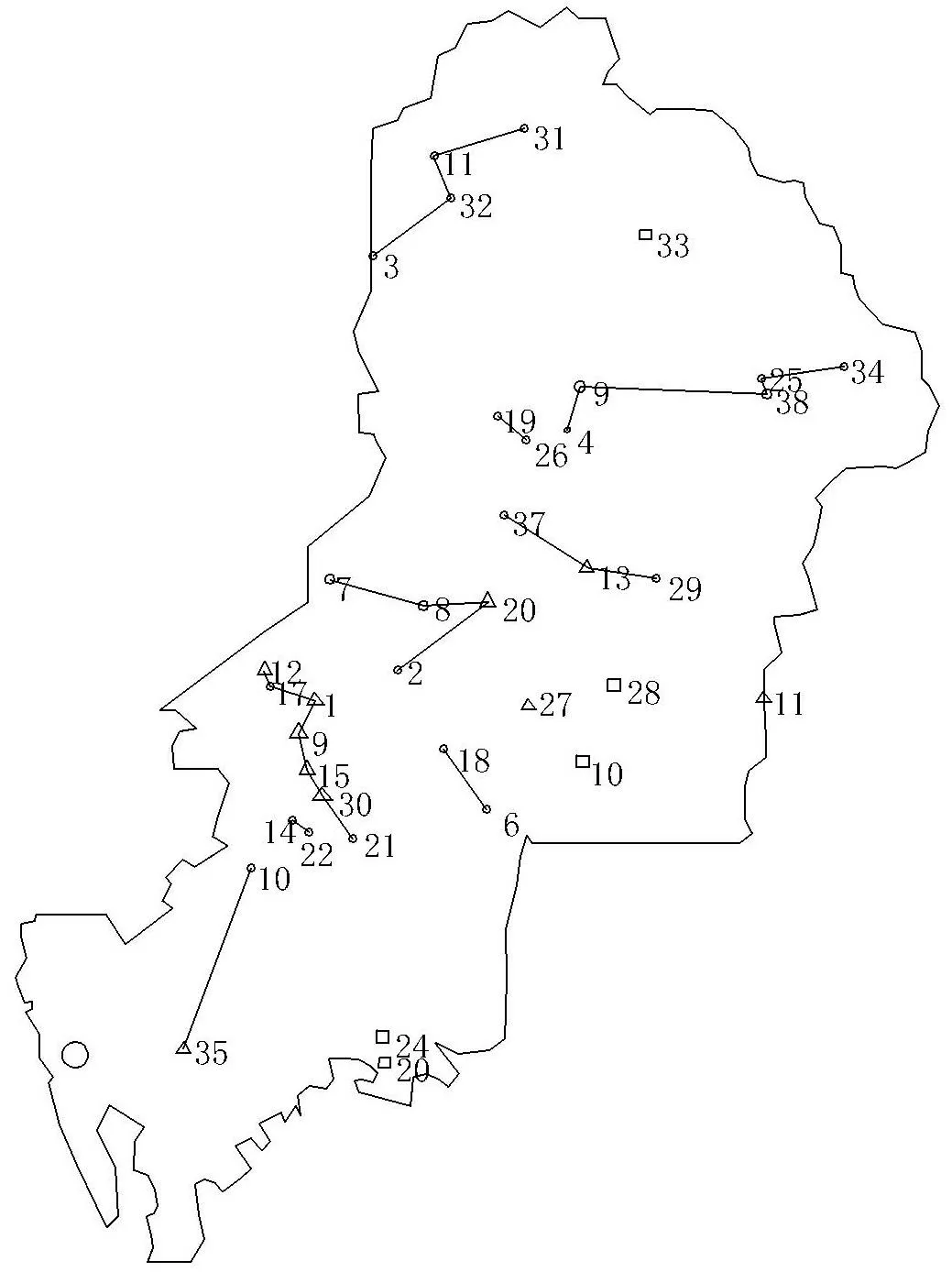
图2　焚烧垃圾运输路线图

本文首先利用k-Means聚类方法将38个垃圾转运站点分成16块，记为P集合，然后采用TSP模型对P集合的垃圾运转路径进行搜索得出焚烧垃圾运输路线分别如图2所示。

本文将三类内部的垃圾站点分别采用k-Means聚类方法分成3块，并记为P1、P2、P3集合，然后采用与处理P集合同样的处理方法对 P1、P2、P3进行处理，得出厨余垃圾的运输路线，结果分别如图3—图5所示。

图3　一区的厨余垃圾运输路线

图4　二区的厨余垃圾运输路线

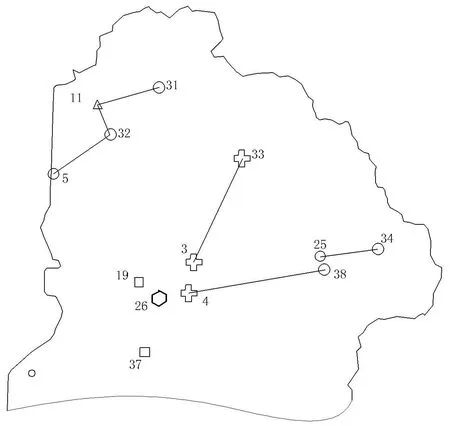
图5　三区的厨余垃圾运输路线

4　模型的有效性分析与建议

针对城市垃圾清运路径规划问题，本文提出了两种聚类模型，主要优点包括：

(1)对于厨余垃圾处理设备的分配问题，分别提出了最短距离聚类模型和k-Means聚类模型，通过比较得出最优解决方案，避免只采用一种方案而导致规划结果不准确。

(2)对于厨余设备的分配问题，本文将厨余垃圾的转运量和转运站到处理中心的距离作为两个重要因素进行分析建模，能较好地解决厨余设备的选址问题，避免了问题的复杂化。

(3)把TSP模型运用到垃圾运输问题上，能有效地解决近距离垃圾转运的重叠问题，从而能有效减少资金投入。

然而，提出的模型仍然存在许多不足之处，主要表现在如下两个方面：

(1)对于垃圾转运站聚类问题，本文考虑的因素较少，没有考虑交通因素、占地费用以及每个地方垃圾量的不确定性等因素，因此所得的结果不够准确。

(2)对于运输中汽车的分配问题，由于提供的数据有限，没有充分考虑汽车运输时的排队问题，容易导致汽车分配不够合理。

4　模型的有效性分析与建议

本文在对城市生活垃圾收运系统各个环节进行深入分析的基础上，结合现代物流理论，以经济最优化为目标，提出了城市垃圾收运系统的优化方法和数学模型，在较准确地解决深圳市南山区垃圾处理问题上，具有一定的通用性，可以推广到全国各大城市的垃圾处理方案设计中以及特定情况下的货物运输问题中。

[参考文献]

[1]Hakimi S L, Hakimi S L. Optimum locations of switching centers and the absolute centers and medians of a graph[J]. Operations Research, 1964, 12(3):450-459.

[2]栗娜,李玲萍.垃圾站选址问题的数学模型及应用[J].物流技术,2011,30(12):135-137.

[3]贾传兴, 彭绪亚, 刘国涛,等. 城市垃圾中转站选址优化模型的建立及其应用[J].环境科学学报, 2006, 26:1927-1931.

[4]刘云斌.城市生活垃圾填埋场选址模糊综合评判系统[D].成都:西南交通大学,2004.

[5]赵静,但琦.数学建模与数学实验[M].北京: 高等教育出版社,2004.

[6]黄雍检,赖明勇.MATLAB语言在运筹学中的应用[M].湖南: 湖南大学出版社,2005.

[7]王祝文,刘菁华,任莉.基于K均值动态聚类分析的地球物理测井岩性分类方法[J].东华理工大学学报：自然科学版, 2009, 32(2):152-156.

[8]吴翊,吴孟达,成礼智.数学建模的理论与实践[M].长沙: 国防科技大学出版社,2009.

Application of Two Clustering Models in Path Planning for Urban Waste Disposal

Wang Long，Liu Shiyu，Hu Jianbo

(InstituteofMechanicalandAutomobile,ChongqingJiaotongUniversity,Chongqing404100,China)

Key Words：urban waste disposal; shortest distance clustering model; k-Means clustering model; path planning

(责任编辑：张凯兵)