一种Web服务组合模型合理性验证方法
2015-12-09胡晓静刘士喜
胡晓静,刘士喜,王 涛
(滁州学院 计算机与信息工程学院,安徽 滁州 239000)
一种Web服务组合模型合理性验证方法
胡晓静,刘士喜,王涛
(滁州学院 计算机与信息工程学院,安徽 滁州 239000)
摘要:为了更加有效地对Web服务组合进行分析验证,设计BPEL到PNML语言的文件转换规则,实现Web服务组合流程的Petri网建模。针对Web服务组合流程设计中可能存在死锁及不正确的流程,在不破坏原Petri网模型结构性质与系统行为的基础上,将其调整映射为自由选择网。在自由选择Petri网理论基础上,设计了一种Web服务组合Petri网模型的合理性验证规则,能在多项式时间内分析网模型的结构活性与有界性,从而避免采用传统的可达树等分析方法出现的状态空间爆炸问题。最后,使用两个具体的Web服务组合Petri网模型证明了本文方法的有效性。
关键词:Web服务; Petri网;合理性验证;自由选择网
中图分类号:TP311
文献标志码:码:A
文章编号:号:2095-4824(2015)03-0016-05
收稿日期:2015-02-12
基金项目:安徽省高校省级科学研究项目(KJ2012Z282);滁州学院自然科学基金资助项目(2011kj008B);滁州学院科研启动基金项目(2012qd09);安徽省自然科学基金项目(1508085MF123)
作者简介:胡晓静(1985-),女,安徽长丰人,滁州学院计算机与信息工程学院讲师,硕士。
Abstract:To analyze and verify the Web Service composition model more effectively, a file transformation rule from the BPEL files to the PNML is designed for establishing the Petri net model of Web Service composition process. In order to detect the deadlock and wrong process of Web Service composition process, the Petri net model is adjusted and mapped to Free Choice net, which is based on the premise that it would not affect the constitutive property and system behavior of the original model. Combining the Commoner theorem with the rank theorem, this paper proposes a rationality verification approach for the Web service composition model, and analyses the structural liveliness and rationality of Free Choice net in polynomial time. Finally, two specific Web Services composition Petri net models are employed to verify the effectiveness of the proposed method.
刘士喜(1982-),男,安徽淮南人,滁州学院计算机与信息工程学院讲师,硕士。
王涛(1979-),男,山东淄博人,滁州学院计算机与信息工程学院讲师,博士。
在Web服务组合建模阶段,组合服务流程可能存在死锁、不可达等问题,因此建立逻辑正确、结构合理的Web组合流程是Web服务组合成功执行的关键。Web服务组合流程合理性验证目的在于对建模阶段所得到的服务组合模型进行动态行为、结构性质的分析,发现其中的异常结构(如死语句、死锁等),保证组合服务在执行前的正确性。BPEL、XLANG、WSFL和WCSI等是主要的Web服务组合流程建模语言[1]。Petri网以其图形化的表现形式、众多的分析方法和坚实的数学基础,成为研究Web服务组合的重要建模工具之一。合理性概念最早是Aalst提出的,用于判断工作流Petri网的有效性和正确性,他提出当且仅当该网系统是活的而且是有界时,工作流网是合理的[2]。Web服务组合Petri网与工作流Petri网类似,判断Web服务组合Petri网的合理性,其本质就是分析该网模型的活性和有界性。活性和有界性是Petri网的重要性质之一,与被模拟的系统的无死锁性密切相关[3]。
Petri网的可达树方法是判断Petri网活性和有界性等特性的重要分析方法之一[4]。然而,采用可达树分析方法对于复杂的Petri网的分析能力不足,容易导致状态空间爆炸等问题。综合国内外研究现状,目前只有Petri网的特殊子类,例如自由选择网才能够有效求解网模型的活性和有界性,以避免状态空间爆炸等问题。Balbo等[5]提出在自由选择网条件下分析工作流Petri网合理性的定理。Desel等[6]给出了Commoner定理和Rank定理,使得不使用可达树、关联矩阵和状态方程等传统方法,而采用多项式方法求解自由选择网的活性与有界性。很多学者基于Desel等的理论,采用多项式方法判断自由选择网的活性和有界性。Kemper等[7]给出了在多项式时间内求解自由选择网有界性与活性的算法。文献[8]结合Commoner定理和Rank定理给出如何获取最小死锁的算法,但未给出求解最小死锁的具体过程和实例验证。文献[9]采用BPEL语言进行Web服务组合建模,通过PNML + OWL 描述自动得到Web 服务组合Petri 网的方法,从而实现Petri网的建模。
在借鉴Petri网和自由选择网理论的活性、有界性研究成果的基础上,本文采用BPEL4WS语言描述Web服务流程,设计了BPEL到PNML语言的文件转换规则,实现Web服务组合流程的Petri网建模。通过将Petri网调整为自由选择网,结合自由选择网中的Commoner定理和Rank定理,给出组合流程合理性验证规则,采用多项式的方式分析网模型的活性及有界性,避免传统可达树等方法带来的状态空间爆炸等问题,以简化模型求解的复杂性。最后,以网系统模型验证该方法的有效性。
1 Web服务组合的Petri网建模
BPEL4WS是为整合现有Web服务而制定的一项规范标准,其目的在于将一组现有的Web服务组合起来,定义一个新的Web服务。
在BPEL文档中,invoke代表一个Web服务,name是Web服务名称,operation 代表Web服务操作,input variable 代表Web服务的输入,output variable 代表Web服务的输出。在Petri网模型中,库所(Place)与Web服务的发生前后相对应,变迁(Transition)对应着Web服务的活动,标记(Token)对应着服务的状态,Petri网的弧(Arc)对应服务流程的关系。
为了实现BPEL文件的Petri网建模,需要借助PNML语言。PNML是一种基于XML的Petri网标记语言,是独立于工具和平台的Petri网文件交换标准。由于BPEL文件与PNML文件都是基于XML语言描述的,因此编写XSLT转换文件,设计BPEL到PNML语言的文件转换规则,可实现BPEL文件的Petri网建模。
下面以BPEL中常见的sequence流程为例,说明BPEL到PNML的文件转换规则。
⑴ 编写XSLT文档,匹配BPEL文件中的process/sequence元素,生成PNML文件的
⑵ 分别建立sequence、invoke元素模板,生成Petri网的变迁(transition)与弧,生成Petri网的输入、输出库所(
⑶ 获取invoke的属性operation值,生成变迁(transition)的名称。生成库所与变迁之间的连接弧,利用position()函数生成连接弧(arc)的起始对象(source)和指向对象(target)。
⑷利用position()函数为PNML文件中的每个元素生成图形信息(
基于BPEL语言描述的Web服务组合Petri网模型的定义如下:
定义1BPEL-PN是一个基本Petri网:N=(P,T; F) ,其中:
⑴ P={p1,p2,……pm}是库所的有限集,代表BPEL4WS流程的发生前条件与发生后条件。
⑵ T={t1,t2,……tn}是变迁的有限集,代表BPEL4WS流程的动作。
⑶ F⊆P×T∪T×P是BPEL流程动作流关系的有限集。
结合工作流网的合理性研究理论,给出BPEL-PN合理性的形式化定义以及判定定理。
定义2BPEL-PN:N=(P,T; F)模型是合理的,当且仅当:
⑴ 对于初始标识Mi(库所i包含一个Token的标识)可达的每一个标识M,存在一个启动顺序使得标识M可达标识M0, 即 ∀M(Mi[*>M→M[*>M0)。
⑵ 标识Mj(库所j包含一个Token标识)是从初始标识可达,则Mj是唯一满足库所j至少包含一个Token的标识,∀M (Mj[*>M∧M≥Mj) →M=Mj。
⑶ 在(N, Mi)中不存在死的转移,∀t∈T ∃M,M’ , Mj[*>M[t> M’。
Web服务组合Petri网的合理性与Petri网的结构活性和有界性密切相关,结合文献[1]给出以下结论。
定理1BPEL-PN网是合理的,当且仅当该网系统N=(P,T; F,Mi)是活的且有界的。
2 BPEL-PN的合理性验证
不合理的Web服务组合流程大多是服务不正确的调用或流程内部节点不正确的连接造成的。Web服务组合流程不合理性主要表现在:流程结构混乱、Petri网模型中存在无界的库所或发生序列、存在死变迁与不活的变迁或变迁发生序列。大多数有效求解一个网模型活性和有界性的算法都是建立在自由选择网的基础上。对于比较复杂的系统模型,一般也是将其转化为自由选择网后进行分析。本文提出的Web服务组合合理性验证过程如图1所示。

图1 合理性验证过程
2.1 模型调整
在BPEL-PN网中,不符合自由选择网结构主要有两种结构类型,分别是反馈结构和不平衡结构[8]。对于反馈结构,在Petri网中存在某个丛,同时有该丛的库所P到变迁T的有向弧和从变迁T到库所P的有向弧(见图2)。对不平衡结构[8],Petri网中存在库所P和变迁T,满足[P]=[T],并且(P,T)不是Petri网中的有向不是Petri网中的有向弧(见图3)。
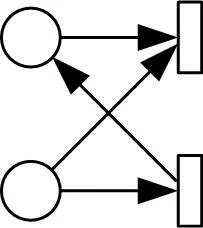
图2反馈结构图3不平衡结构
定义映射φ1和φ2,将不符合自由选择网的Petri模型调整为(扩展)自由选择网。由于网的丛是有限的,因此经过有限步的调整后,可以把Petri网调整为自由选择网。调整后的网系统与原网具有相同的结构活性和结构有界性,这种调整不会改变系统的结构特性[6]。
定义3[8]令N是一个BPEL4-PN,映射φ1(N)定义为对N中每个反馈结构移去弧(t,p),增加新的库所 p’和新的变迁t’,增加新的弧(t,p’)、(p’,t’)和(t’,p)。反馈结构调整过程如图4所示。映射φ1(N)定义为对N中的每个不平衡结构增加新的弧(p,t)和(t,p)。不平衡结构调整过程如图5所示。
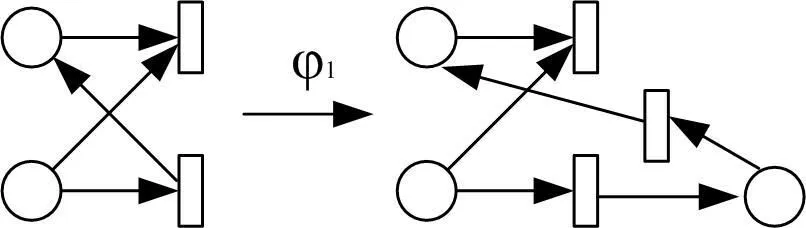
图4 反馈结构调整
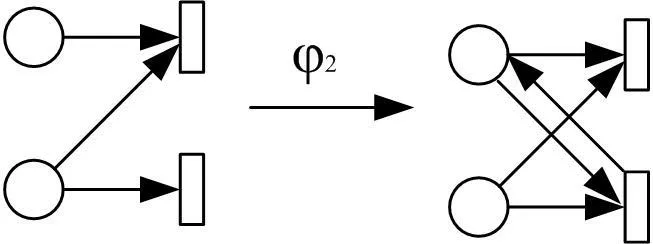
图5 不平衡结构调整
2.2 合理性验证
将Petri网模型经过有限次映射后调整为自由选择网,构造该网模型的求解合理性算法。在提出Web服务组合的合理性定理前,引入两个与自由选择网的活性和有界性有关的定理。
定义4[6]设X是网N=(P,T; F)节点的集合,[X]表示X的丛,当且仅当满足下列条件:
⑴ X∈[X];
⑵ 如果库所p∈[X],则也有p·∈[X];
⑶ 如果变迁t∈[X],则也有·t∈[X]。
定义5[11]虹吸 N= (P, T; F)为一个Petri网,一个非空集合S⊆P是虹吸当且仅当·S⊆S·。
定义6[11]陷阱 N= (P, T; F)为一个Petri网,一个非空集合S⊆P是陷阱当且仅当S·⊆S·。
定理2[6]Commoner定理 自由选择网系统(N, M0)是活的,当且仅当网系统的每一个虹吸都包含一个被M0标识的陷阱。
定理3[6]Rank定理 (扩展)自由选择网N=(P,T; F)是结构有界且结构活的,当且仅当满足以下条件:
⑴ N存在正的P-不变量;
⑵ N存在正的T-不变量;
⑶ |A| = Rank(N) + 1,其中Rank(N)是网N关联矩阵的秩,A是网N的丛集合。
根据Petri网结构有界和Petri网系统有界性定义及性质,一个Petri网是结构有界的,则该Petri网系统也必然是有界的[3]。因此,当一个自由选择网满足定理2与定理3,其必然是结构有界并且活的。本文在以上定理的基础上,给出BPEL-PN网系统的合理性判断定理。
定理4BPEL-PN合理性 Web服务组合Petri网系统(N,Mi)是合理的,当且仅当调整后的(扩展)自由选择网(N’,Mi’):
⑴ N’有正的S-不变量;
⑵ N’有正的T-不变量;
⑶ |C N’| = Rank(N’) + 1
⑷ 网系统每个虹吸都包含一个被Mi’标识的陷阱。
定理5[2]设N=(P,T;F)为一个网,C为N的关联矩阵。p1={pi1,pi2,……pik}为网的一个虹吸(陷阱)的充分必要条件是:C关于P1列的列生成子阵中,每个非全零行至少包含一个“-1”或“1”元素。
3 模型验证
以两个具体的Web服务组合Petri网模型,验证BPEL-PN合理性判断定理是否有效。图6是通过映射φ2调整后的扩展自由选择网。
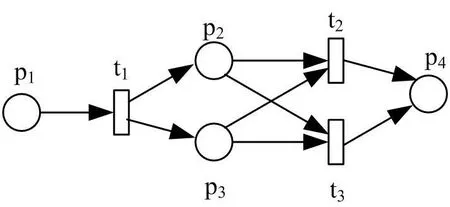
图6 调整后的网模型
根据合理性定理,判断该模型的合理性步骤如下:
⑴ 根据扩展自由选择网的定义,调整后的网模型是一个扩展自由选择网。
⑵ 求解此网的关联矩阵C,对关联矩阵C进行行初等变换,变换成阶梯矩阵求关联矩阵的秩。
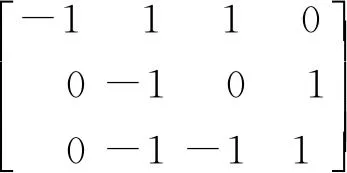
⑶阶梯矩阵中有3行元素不全为零,因此Rank(N)=3。根据丛的定义,该网丛的集合为A={(p1,t1),(p2,p3,t2,t3),(p4)} ,丛的集合个数为3,不符合BPEL-PN合理性定理。
⑷ 根据定理5计算,网的虹吸有{p1,p2},{p1,p2,p3},{p1,p2,p4}。陷阱为{p2,p4}不符合BPEL-PN合理性定理。
⑸ 根据合理性定理判断该网是不合理的。
图7是一个经过映射φ1与φ2调整后的Web服务组合Petri网模型。
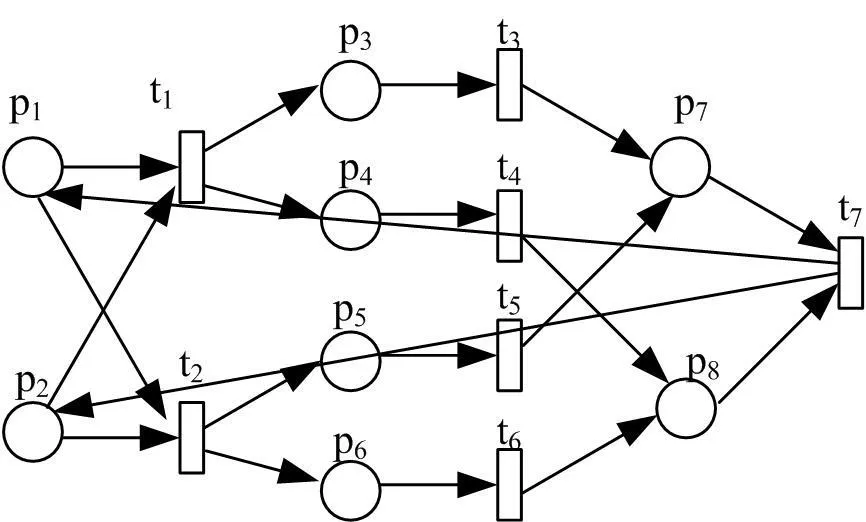
图7 扩展自由选择网模型
根据合理性定理,判断该模型的合理性步骤如下:
⑴ 根据扩展自由选择网的定义,该模型是一个扩展自由选择网。
⑵ 求解此网的关联矩阵C。对关联矩阵C进行行初等变换,化成阶梯矩阵求关联矩阵的秩。

⑶ 阶梯矩阵中有5行元素不全为零,因此Rank(N)=5。根据丛的定义,该网丛的集合为A={(p1,t1,t2,p2),(p3,t3),(p4,t4),(p5,t5),(p6,t6),(p7,t7,p8)} ,丛的集合个数为6,符合BPEL-PN合理性定理。
⑷ 求解此网的一个P-不变量与T-不变量,其中(1,1,1,1,1,1,1,1)是一个正的P-不变量,(1,1,1,1,1,1,2)是一个正的T-不变量。
⑸根据定理5计算,上述网的虹吸有{p1,p3,p4,p5,p6,p7},{p1,p3,p4,p5,p6,p8},{p2,p3,p4,p5,p6,p7},{p2,p3,p4,p5,p6,p8}。陷阱为{p1,p3,p5,p7,p8},{p1,p4,p5,p7,p8},{p1,p3,p6,p7,p8},{p1,p4,p6,p7,p8},{p2,p3,p5,p7,p8},{p2,p4,p5,p7,p8},{p2,p3,p6,p7,p8},{p2,p4,p6,p7,p8},网的每个虹吸都包含一个被标识的陷阱,符合BPEL-PN合理性定理。
⑹根据合理性定理,可以判断该网结构是合理的。
4 结束语
在Petri网和自由选择网理论的活性、有界性研究成果的基础上,采用BPEL语言组合Web服务,设计了从BPEL到PNML语言的文件转换规则,实现了Web服务组合的Petri网建模。在自由选择Petri网已有的理论基础上,给出一种Web服务组合Petri网模型的合理性验证规则,采用多项式方法,分析网模型的活性及有界性,避免传统可达树等方法带来的状态空间爆炸等问题,简化了模型求解的复杂性。但对于复杂的Web服务组合网模型,如何在不破坏原网结构性质的基础上将网调整为自由选择网,再利用给出的合理性验证方法进行验证,还需进一步研究。
[参考文献]
[1]Saleem M Q. A decade of model driven Web services composition frameworks[J].Research Journal of Applied Sciences, Engineering and Technology,2014, 7(20): 4244-4250
[2]Vander A W, VanHee K. Workflow management: models, methods and system[M].The MIT Press, 2002.
[3]吴哲辉.Petri网导论[M].北京:机械工业出版社,2006.
[4]Cardinale Y, Haddad J E, Manouvrier M ,et al. Web service composition based on Petri nets: review and contribution[M].Springer Berlin Heidelberg, 2013.
[5]Aalst van der W M P. Verification of workflow nets[J].Computer Science, 1997, 48(12): 407-426.
[6]Desel J, Esparza J. Free choice Petri nets[M].Cambridge University Press, 1995.
[7]Kemper P, Bause F. An efficient polynomial-time algorithm to decide liveness and boundedness of free-choice nets[C]// Proceedings of the 13th International Conference on Application and Theory of Petri Nets. Springer-Verlag, 1992:263-278.
[8]陈翔,夏国平,李涛.基于Petri 网的工作流模型合理性研究[J].北京理工大学学报, 2004,24(12):1074-1078.
[9]马炳先,相东明,张正明. Web 服务组合的Petri 网自动生成方法[J].小型微型计算机系统,2013,34(2):332-337.
[10]刘士喜,胡晓静.BPEL到PNML文件转换框架的设计与实现[J].计算机应用与软件,2013,30(5):60-64.
[11]张金泉,倪丽,蒋昌俊,等.Petri 网极小虹吸的计算方法与性能分析[J].计算机学报,2010,33(3):576-602.
A Rationality Verification Approach for Web Services Composition Model
Hu Xiaojing, Liu Shixi, Wang Tao
(SchoolofComputerandInformationEngineering,ChuzhouUniversity,Chuzhou,Anhui239000,China)
Key Words:Web service; Petri net; rationality verification; free choice net
(责任编辑:张凯兵)
