山东沿海测风高度对风速的影响和订正研究

孙莎莎，吴 炜，郭俊建

（山东省气象台，山东济南250031）

山东沿海测风高度对风速的影响和订正研究

孙莎莎，吴 炜，郭俊建

（山东省气象台，山东济南250031）

利用2009年1月—2011年5月山东的19个测风塔风资料，分析研究测风塔不同高度观测风数据之间的相关性，进而研究不同测站高度对风资料代表性的影响，并在此基础上寻找对现有风场进行订正比较有效的方法与技术。

不同高度；测风塔；订正

1引言

山东濒临黄渤海，海上大风、海雾、强对流、台风、风暴潮等这些海洋灾害性天气都对经济社会发展及人民生命财产安全构成了严重威胁。近年来，中国气象局和山东省政府均加大了对海洋气象监测及预报预警方面的投入。目前山东省沿海区域气象观测站500多个，测站种类有海岛站、浮标站、船舶站、海上石油平台站、风廓线仪、测风塔以及移动气象台等，可以实时获得大量的海上风资料。这些实时资料在预报员们准确预报天气过程中起到了重要作用，但同时这些观测站受布设条件所限所处地理位置复杂且分布不平衡；另外受沿海地形的影响，观测站点的布设存在高度不一致问题，这些问题严重限制了海上大风预报准确率的提高。

许多学者研究过高度对风场的影响，海洋石油研究所工程实验室等[1]对渤海的海上风速观测资料进行分析，发现该地区的风速廓线指数定律要比对数定律更加适用。曾旭斌等［2］从近地层的通量—梯度关系出发，在稳定层结得到了改进的风廓线公式并验证发现该公式适合140m以下的大气，误差较小。杨林［3］根据福建省气象铁塔所观测的一年风、温资料，对近地层垂直温度梯度、风随高度的变化和海陆风进行统计计算和分析研究，从中得出我国中低纬度地区海陆边界层100m以下环境大气变化的若干气象特征的认识。王日东等［4］研究了新建海岛站与原有长岛站大风的关系，将海岛站与沿岸站大风进行对比分析。王静［5］研究发现青岛地区风速廓线基本遵循随高度升高递增的规律，在低层风速随高度增加比较显著，基本符合幂指数分布规律，500m以上风速随高度的变化己不再明显。

本文通过分析山东测风塔不同高度观测风数据之间的相关性，研究不同测站高度对风资料代表性的影响和订正使用的方法与技术。

2确定不同高度风的相关拟合方程

2.1 资料和方法

山东省共19个测风塔，主要集中在滨州、东营、潍坊、烟台、威海、青岛和日照，在这些地区风速不容易发生突变并且风向也比较稳定。这种地理位置使测风塔观测到的风场资料对沿海和近海风场分析订正有很高的参考价值。本文所用资料的时间序列长度是从2009年1月—2011年5月，时间分辨率是10m in。所有测风塔都有3个不同的测风高度，分别是10m、50m和70m，使用的观测要素有平均风速、最大风速以及极大风速。对不同高度的风场资料数据进行统计分析和相关性分析等处理。

2.2 计算分析确定拟合方程

由于19个测风塔本身所处的海拔不同，这些测风塔10m测风高度的风速代表不了海平面10m高度的实际风速，给实际业务应用造成了一定的困难。由于业务上需要把这些测风塔测得的风速订正到海平面真正10m高度上，因此需要通过研究测站高度对风资料代表性的影响和订正使用的方法，确定一个比较可行的风速随高度的变化关系，利用该关系对一定适用的空间范围内的观测站的任意高度的风速进行订正。由于岸基其他类型的观测站的风速都是基于10m海拔高度上的，因此将风速订正到10m的海拔高度，这样可以得到比较直观且相对全面的山东省10m海拔高度的风场描述。

在大气扰动的理论研究中，精确测定近地层风廓线是一项基本任务。大气边界层中风随高度变化主要遵循指数定律和对数定律方程，只需要一个特定的参数，就可以从一个高度的风速推算另一个高度的风速。

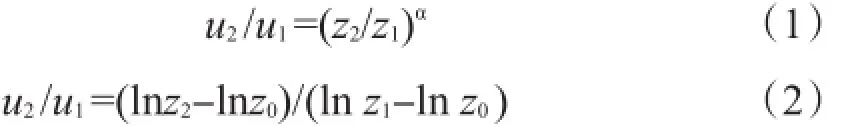
公式（1）为指数定律，公式（2）为对数定律。式中：u1、u2为风速；z1、z2为高度；z0为粗糙度；α为幂指数。参考以前学者对沿海地区近地层风随高度变化特征的研究以及指数定律和对数定律各自的适用范围和特点，结合山东省的沿海地理位置特点，因此采用指数定律对山东省测风塔的风速资料进行处理分析。处理的基本思路是：α幂指数与大气层结状态有关，风速的大小对应不同的大气层结状态。为了更好地研究α幂指数的分布，将测风塔10m高度观测风速分为6级（10.8m/s）及以上大风和6级以下风两种情况。

当测风塔10m高度观测风速在6级及以上时，由于测风塔本身的有3个测风高度，除了10m以外还有50m和70m两个测风高度。将测风塔10m高度观测风速和50m高度观测风速设为第1组数据，将测风塔10m高度观测风速和70m高度观测风速设为第2组数据，把这两组观测风速数据代入指数公式：

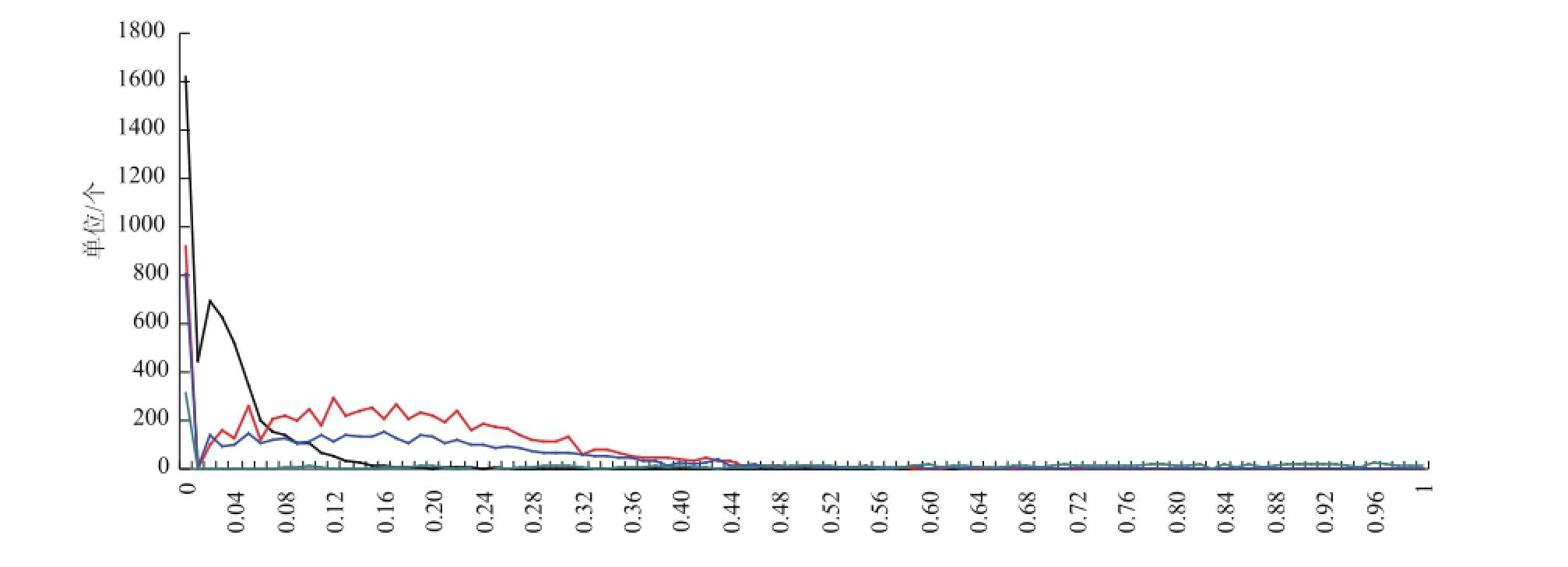
图1 6级以上大风的10m和50m的α值分布

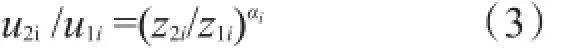
其中u1i代表第i个时间序列的50m或者70m高度的风速；u2i代表第i个时间序列的10m高度的风速；z1i代表第i个时间序列50m或70m的测风高度；z2i代表第i个时间序列10m的测风高度；αi为第i个时间序列的幂指数。对于同一个测风塔，u1i、u2i都是一维数组，长度是时间序列i，这样我们通过变换指数公式得到下面的公式：

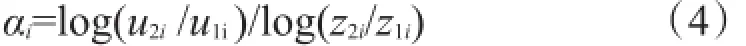
根据该公式计算得到α幂指数的数值。当测风塔10m高度观测风速在6级以下时，也是类似方法计算α幂指数。

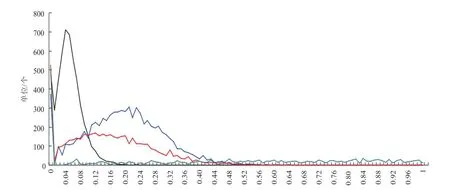
图2 6级以上大风的10m和70m的α值分布

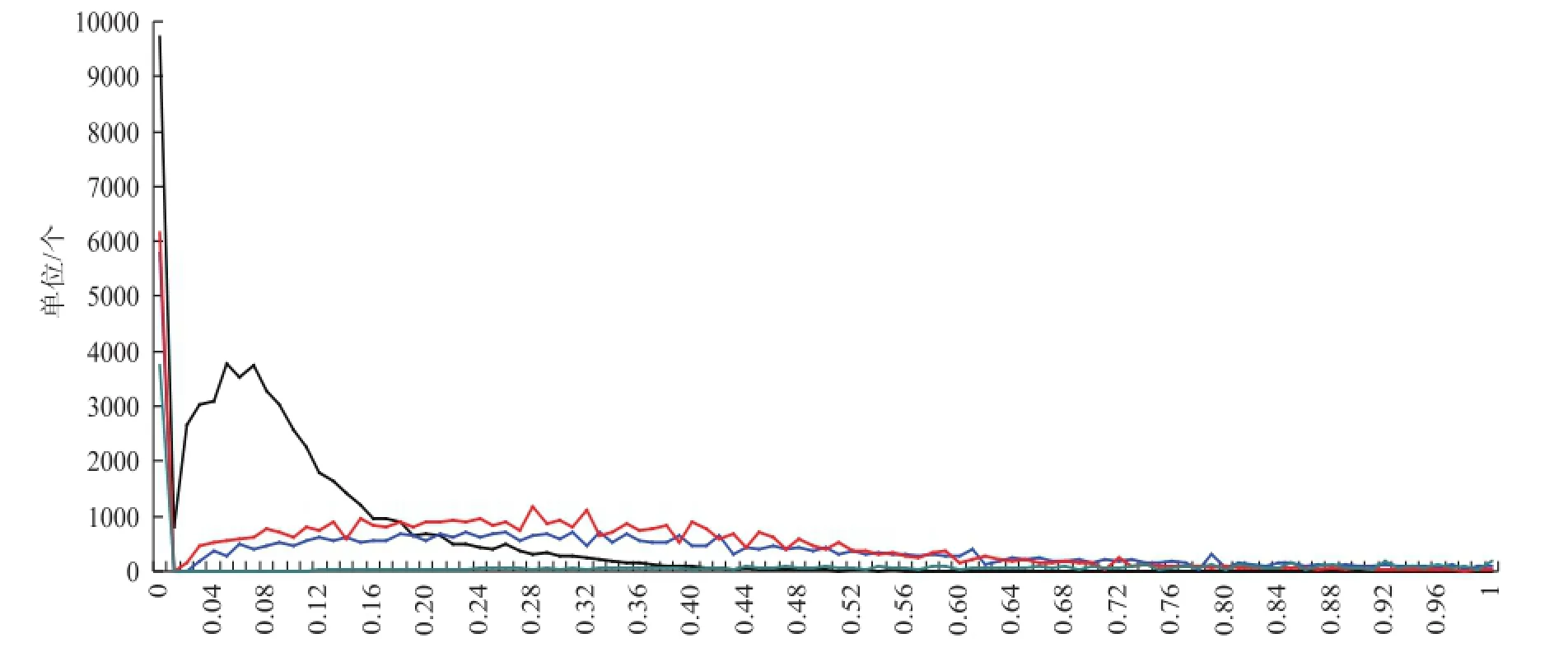
图3 6级以下风的10m和50m的α值分布

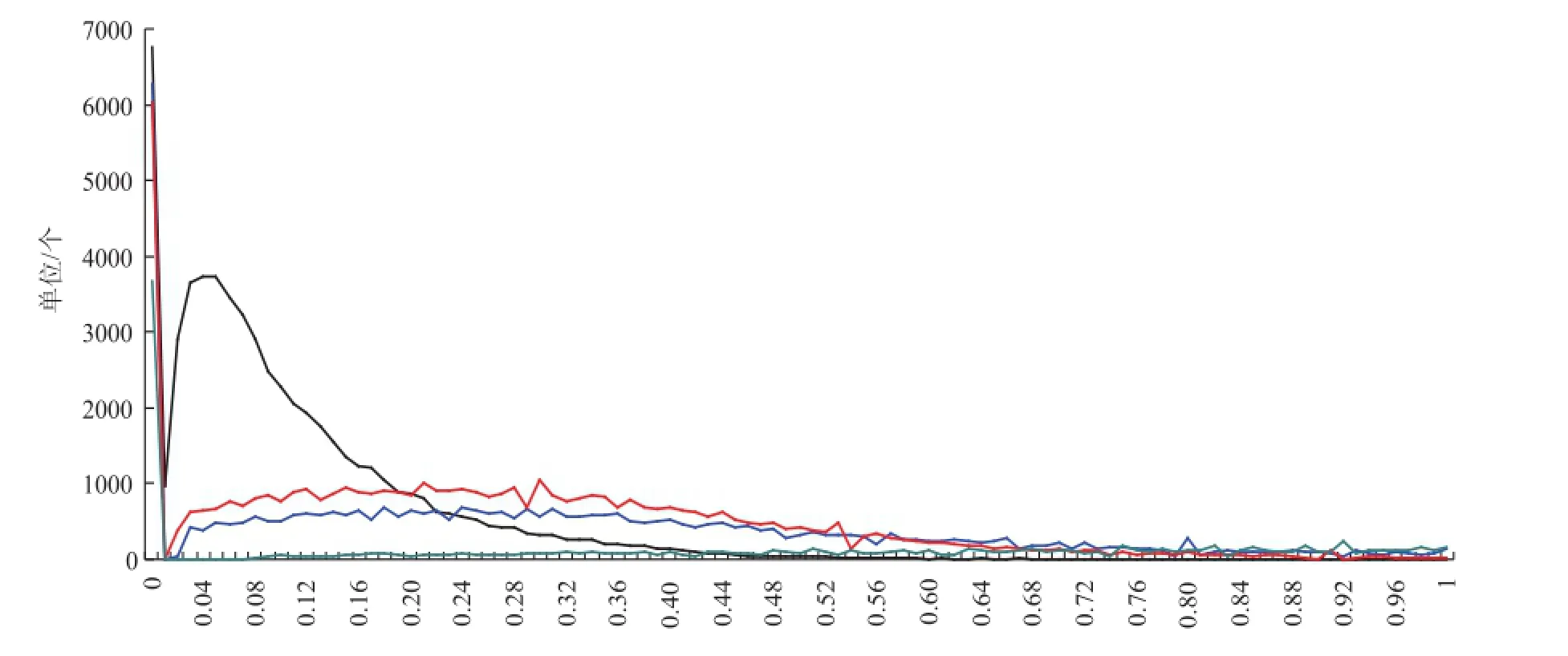
图4 6级以下风的10m和70m的α值分布

选取4个不同海拔高度的测风塔，其中15001

代表海拔高度10m以内的测风塔，15010代表海拔高度10—50m之间的测风塔，15009代表海拔高度50—100m之间的测风塔，15012代表海拔高度100m以上的测风塔，分别给出测风塔10m高度观测风速在6级及以上、6级以下时的α幂指数分布，结果如图1—4所示，发现：无论测风塔10m高度观测风速在6级及以上还是6级以下，不同测风高度之间的α幂指数都不是一个固定的数值，都存在一定的分布区间。

通过对4个代表测风塔不同梯度的α值分布图分析发现，对于同一个测风塔，α幂指数在一定的范围内波动，而对风场订正需要确定一个适用的α幂指数，于是将α幂指数设为从0.00—1.00间隔为0.01的101个数值，依次把这101个α幂指数代入变换后的指数公式：

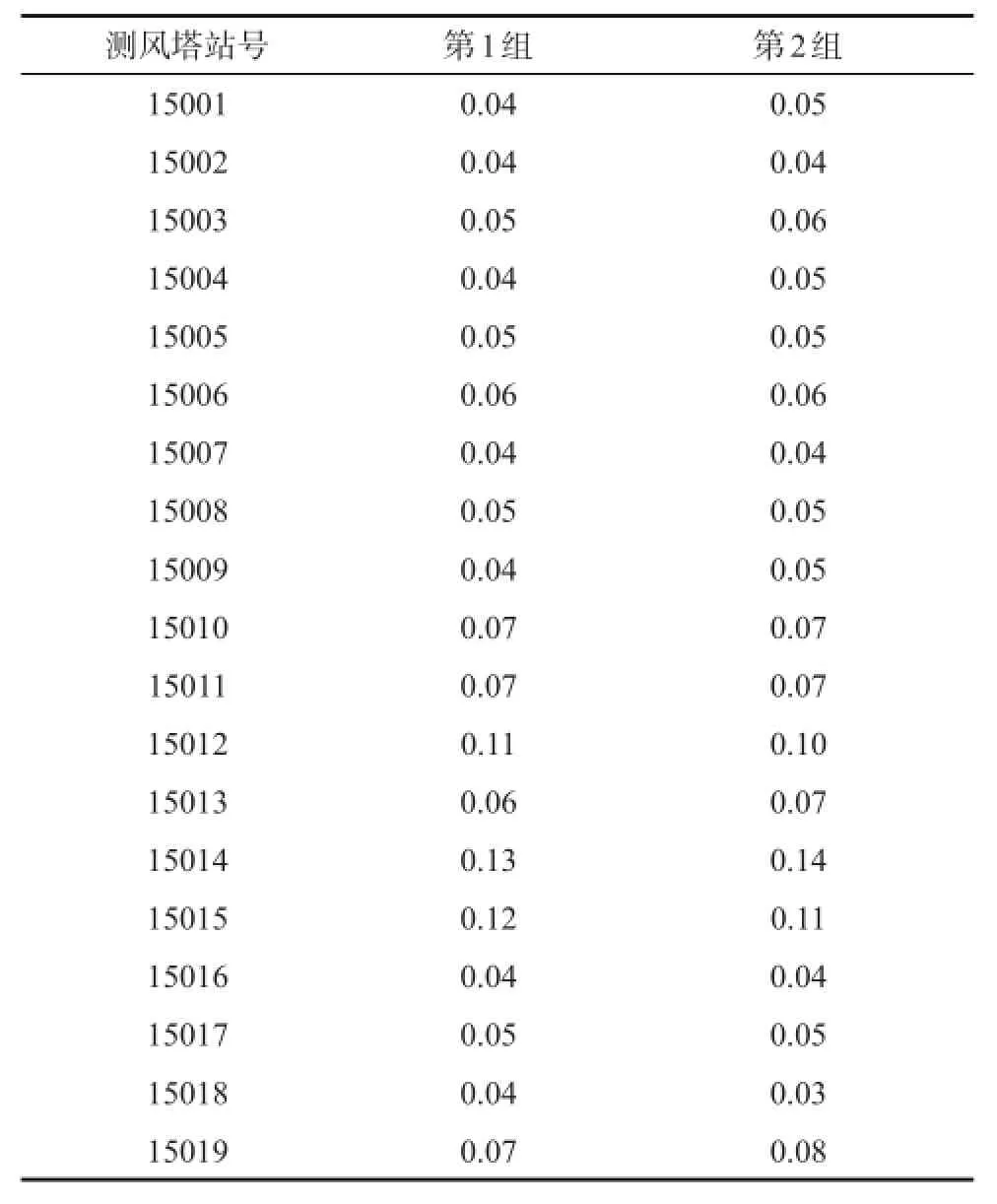
表1 10m高度风大于等于6级的10m和50m、10m和70m两组α值

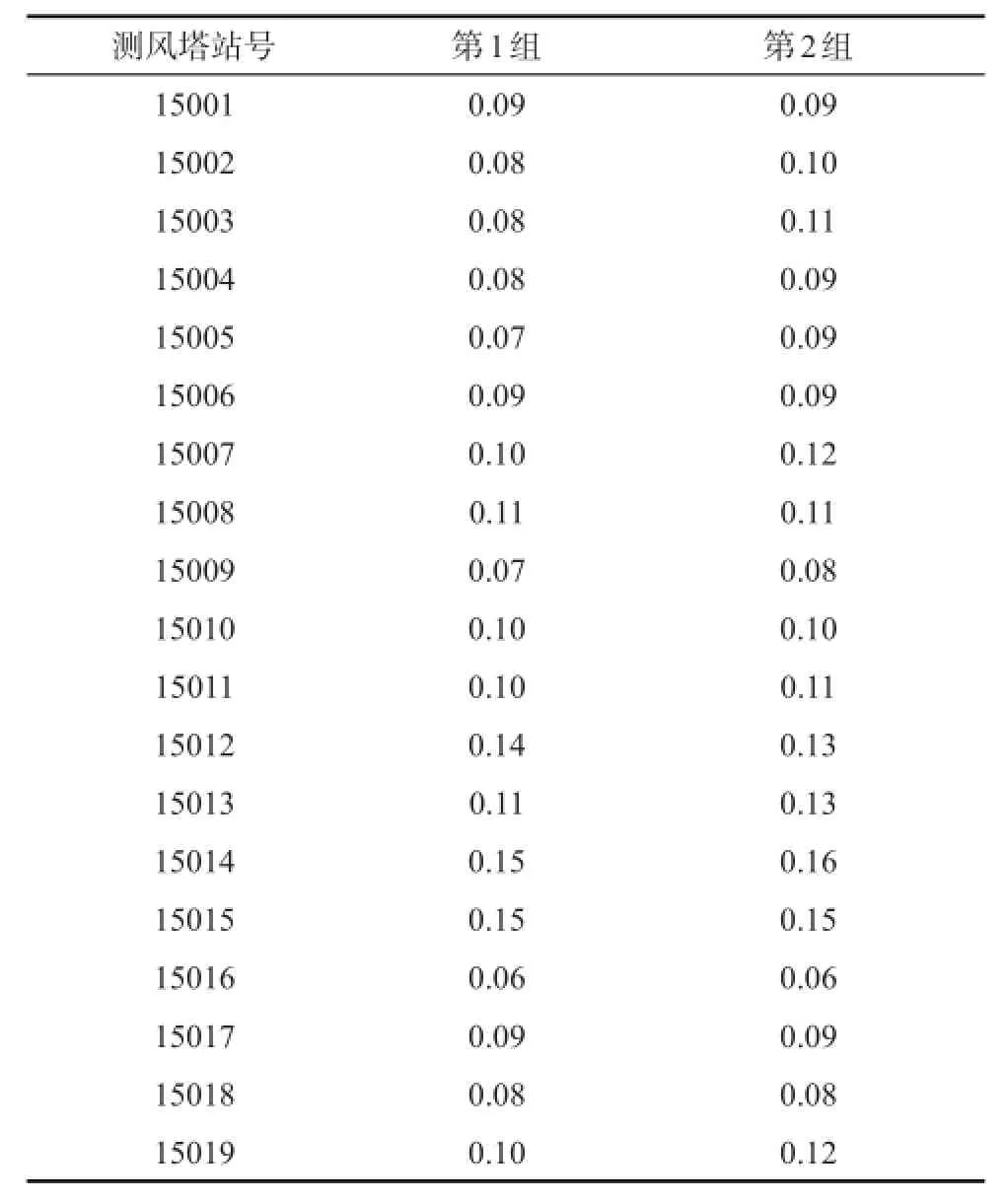
表2 10m高度风速小于6级时10m和50m、10m和70m两组α值

同时代入50m或70m测风高度的风速u1i就能推导出10m测风高度的估计风速u2i，也可求出所有时间序列的实测风速u2i和估计风速u2i差值平方总和，在该差值平方总和为最小值的条件下得到一个确定的α幂指数。此外，参考统计的测风塔所有时间序列α幂指数的出现频率分布情况，最后选取的α幂指数需满足实测和估计风速误差最小且出现频率较高。

计算得到的α幂指数存在如下特点（表1和表2）：总体来说，测风塔10m高度的观测风速6级及以上的两组α幂指数值要小于6级以下的α幂指数值。无论10m高度观测风速是大还是小，同一个测风塔的第一组（10 m和50 m）和第二组（10 m和70m）的α幂指数值都很接近。海拔高度在10m以下站号为15001—15008的测风塔，10m高度的观测风速在6级及以上的α幂指数在0.04—0.06的范围内，10m高度的观测风速在6级以下的α幂指数在0.07—0.12的范围内;海拔高度在10m以下站号为15013—15015的测风塔，10m高度的观测风速在6级及以上的α幂指数在0.06—0.14的范围内，10m高度的观测风速在6级以下的α幂指数在0.11—0.16的范围内。海拔在10—100m的测风塔，10m高度的观测风速在6级及以上的α幂指数在0.03—0.08的范围内，10m高度的观测风速在6级以下的α幂指数在0.06—0.12的范围内。海拔高度在100m以上

的测风塔15012，10 m高度的观测风速在6级及以上的α幂指数在0.10—0.11范围内，在6级以下的α幂指数在0.13—0.14范围内。

根据α幂指数的物理意义：反映大气层结状态。当大气不稳定时，扰动易于发生或加强，动量上下交换激烈，上下层风速差别变缓，α值就小。大气稳定时就相反，不利于动量交换，上下风速差别变大，α值就大。α值随大气的不稳定度增加而减小，本文分析结果表明α值存在随风速增加而减小的特点。

同时，α幂指数随地理位置变化而发生变化。海拔高度都在10 m以下，站号15001—15008的测风塔的α幂指数值比较接近，15013、15014和15015这3个测风塔的α幂指数值比较接近，并高于15001—15008测风塔的α幂指数值。这些测风站海拔高度相近，但是α幂指数存在较明显的差别可能是于周围的观测环境有关系，15013、15014和15015这3个测风塔都是位于威海的泊于镇夏庄村，是山东半岛东端，三面濒临海，全年平均风速都比较大，一年中发生大风的频率也比较高，这可能是α幂指数值比较高的原因。

3不同高度风订正到10m标准面风场

前面对测风塔的风资料进行处理分析，确定出不同高度风场之间的拟合方程:

同时也得到不同风塔的α幂指数值，接下来利用拟合方程把海拔高度不一的自动站的观测风场订正到海拔10m的高度上，将订正后的风场、自动站观测风场和欧洲中心细网格10m风场00时起报场进行对比，根据订正后的10m风场是否合理，来检验拟合方程，结果发现：在山东半岛丘陵地区以及其他海拔较高的地区，订正风场比观测风场更接近于欧洲中心细网格10m风场，观测风场的风速在这些海拔比较高的地区风速大于欧洲中心细网格10m风场，更大于订正风场；在海拔较低的平原地区，观测风场、订正风场、欧洲中心细网格10m风场三者都比较接近。由此看出，本文的风场订正方法有一定的可靠性。

由于测风塔沿海分布相对均匀，并且测风塔的风场资料和其他测站的资料存在较好的相关性，通过其资料计算出的α值在一定的范围内具有代表性，周围的自动站可以直接使用附近的测风塔α值。本文根据自动站和测风塔的经度纬度计算它们之间的平面距离，最后选取距离自动站最近的一个测风塔，取该测风塔的α值来代替自动站站的α值，因此根据下面的公式：

式中：u1i代表第i个时间序列的某个自动站的观测风速；z1i代表第i个时间序列该自动站的海拔高度；u2i代表第i个时间序列的该自动站订正到海拔10m高度的风速；z2i为常数10，代表10m海拔高度，可以计算得到需要的时间序列的海拔10m高度的订正风场。

4总结与分析

通过以上的研究，主要得到如下结论：

（1）通过对测风塔测风资料进行统计分析和数据处理，确定不同高度风场的订正公式：u2/u1=(z2/z1)α，并且发现公式中指数参数有如下特点：α值随风速增加而减小；α的值随地理位置变化而发生变化；

（2）利用确定的不同高度风场的订正公式：u2/ u1=(z2/z1)α对区域自动站风场进行订正，得到10m高度的标准面风场；

（3）使用该风场订正方法，可以有效的提高观测资料的可用性，一定程度上解决业务急需问题，并为开展海上大风预报技术研究提供帮助。

[1]海洋石油研究所工程实验室,天津市气象局,中央气象局天气气候研究所应用气候组.渤海某处风速梯度观测资料的分析[J].气象,1978,(6):38-40.

[2]曾旭斌,赵鸣,苗曼倩.稳定层结140米以下风廓线的研究[J].大气科学,1987,11(2):153-159.

[3]杨林.海陆边界层气象特征的分析[J].气象科技,1998,(2):57-60.

[4]王日东,姜俊玲,郭卫华,等.渤海海峡海岛站与沿岸站大风对比分析[J].海洋预报,2010,27(2):22-29.

[5]王静.青岛市大气边界层气候特征研究[D].兰州:兰州大学, 2011.

Study ofw ind observation heightsof shandong coasteffect on w ind speed and how to correct theeffect

SUN Sha-sha,WUWei,GUO Jun-jian
(Shandong ProvincialMeteorologicalBureau,Jinan 250031China)

Based on the w ind data at 19 w ind towers in Shandong from January 2009 to May 2011,the correlation between the different heightw ind fields of wind towers is analyzed,and then the effectof different heightsof station onw ind isstudied,and an effective correctmethod is revealed.

differentheights;w ind tower;correct

P732

A

1003-0239（2015）06-0034-06

2015-04-16

山东省气象局预报员专项项目(sdyby2012-19);山东省气象局青年科研基金项目（2015SDQN02）

孙莎莎（1985-），女，工程师，硕士，从事天气预报工作。E-mail:sunss-08@163.com

10.11737/j.issn.1003-0239.2015.06.005