采样间隔和插值对混沌系统可预报期限估计的影响

史 珍，丁瑞强，李建平，王彰贵

（1．北京大学物理学院，北京100871；2.国家海洋环境预报中心，国家海洋局海洋灾害预报技术研究重点实验室，北京100081；3.中国科学院大气物理研究所大气科学和流体力学数值模拟国家重点实验室，北京100029；4.北京师范大学全球变化与地球系统科学研究院，北京100875；5.全球变化联合研究中心，北京100875）

采样间隔和插值对混沌系统可预报期限估计的影响

史 珍1,2，丁瑞强3，李建平4,5，王彰贵2

（1．北京大学物理学院，北京100871；2.国家海洋环境预报中心，国家海洋局海洋灾害预报技术研究重点实验室，北京100081；3.中国科学院大气物理研究所大气科学和流体力学数值模拟国家重点实验室，北京100029；4.北京师范大学全球变化与地球系统科学研究院，北京100875；5.全球变化联合研究中心，北京100875）

利用非线性局部Lyapunov指数的方法研究了采样间隔和插值对混沌系统可预报性的影响，结果表明：在一定范围内，采样间隔对系统可预报期限估计的影响基本是随采样间隔的增大而逐渐减小。但当采样间隔超过一定大小时，所得序列已不能找到真实的局地动力相似，无法得到其真实的误差增长情况，也无法得到系统准确的可预报期限的估计。本文通过插值的方法试图还原同样长度的时间序列，结果表明不论是在采样间隔较大还是较小的情况下，插值都不能有效地改善对系统可预报期限的估计。此外，在采样间隔固定的情况下，随着插值个数的增多，系统的可预报期限的估计反而更低。以上结果提示我们在利用实际海洋观测资料估计其可预报期限时，选用较高分辨率较长时间序列的资料可以得到更接近真实的可预报期限。

非线性局部Lyapunov指数；可预报性；混沌系统

1引言

混沌系统由于其固有的内在随机性，存在一个可预报上限[1-3]。海洋作为复杂的非线性动力系统，具有混沌特性，定量地估计海洋的可预报性对海洋预报的产品及业务化预报结果具有非常重要的现实意义[4-9]。如何定量的给出可预报期限，是可预报性研究的一个重要课题[10-12]。过去的许多研究是基于最大Lyapunov指数来刻画混沌系统预报误差的整体（长期）平均增长速率，其倒数被近似表示为最大可预报时间长度[13-15]。然而，由于该指数假设初始扰动无限小，误差发展方程近似满足切线性方程，属于误差的线性增长理论的范畴，忽略了误差非线性增长阶段对可预报性的贡献，并不能描述有限尺度大小初始误差的情形，因此存在着很大的缺陷和不足[16-18]。近年来，李建平[19]、丁瑞强等[20]和Ding等[18]引入了非线性局部Lyapunov指数(NLLE)的方法，克服了传统Lyapunov指数的局限性，可以很好地表征有限尺度大小初始扰动的非线性增长，能够定量地确定混沌系统的可预报期限。在混沌系统的控制方程已准确获知的情况下，可以直接数值积分混沌系统的控制方程及其误差发展方程，来计算NLLE及其相关统计量，从而定量地确定可预报期限。在混沌系统的控制方程未知的情况下，可以对混沌系统某个变量的实验或者观测数据通过寻找局部动力相似点的方法来确定NLLE，从而定量地估计可预报期限[21-23]。

现实中，海洋的实际观测资料由于受到观测上，传输上，设备上，技术上等方面的原因，会不可避免地存在有噪声的污染，或者在采样的时间间隔上受到限制。这些因素会直接影响时空资料的质量和数量，进而影响到预报结果的准确性[24-26]。弄清这些因素对时空序列可预报性的影响，将有助于我们提高并改善预测结果。史珍等[27]在2012年利

用NLLE方法研究了在初始误差存在的情况下，随机误差即白噪声对混沌系统可预报性的影响。结果表明：初始误差和随机误差对可预报期限影响所起的作用大小主要取决于两者的相对大小，此外滤波并不能有效地改善对系统可预报期限的估计，如何提高包含较大随机误差的实际观测资料可预报期限的估计仍面临很大困难。那么对于采用不同时间间隔的采样条件下产生的时空序列，其可预报性的估计是否会受到不同采样间隔的影响？若有，是否可以通过插值的方法将它们还原成原序列长度减小甚至去除这种影响？同时，对于采样间隔较长的物理量所得到的资料长度相对较短，对于这些较短长度的资料，为了满足一些计算上的要求，通常可以通过插值的方法来得到一个较长的时间序列，而这种由插值后得到的较长序列其可预报期限的估计相对于真实序列的可预报性又会有怎样的变化？不同的插值间隔是否会对序列可预报性的估计造成影响，是否存在一个合适的插值间隔使得在该插值间隔下得到序列的可预报性最接近真实的可预报性？本文将利用NLLE方法来讨论以上问题，所得结果将对认识采样频率和插值对海洋可预报性的影响有一定的启示意义。

2试验设计

本文选用Lorenz系统方程[1]来研究采样与插值的问题，

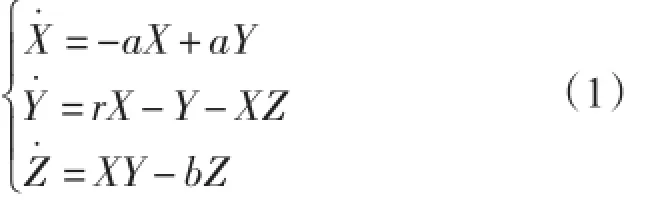
式中：a为Prandtl数，r为Rayleigh数，b表示所研究对流区域的外形比参数。这里我们选取参数值a=10，r=28，b=8/3。

假设我们已经获得某个混沌系统第i个单变量的N长度的试验数据，，其原始采样间隔即为其步长，记为Δt=1。对于该试验数据，采用不同的时间间隔nΔt，可以得到长度为的新序列（这里用[]表示向上取整），记为对于该新序列，通过插值的方法将其插值成时间间隔为n′Δt的序列，此时序列长度插值后序列为yi(N′)=yi1,yi2,yi3,...,yiN′，需要讨论以下3个问题：

（1）采样间隔问题。对于不同的采样间隔，可以得到不同长度的时间序列，利用非线性局部Lyapunov指数来估计它们的可预报性，并与原始序列的可预报性做对比，探讨不同采样间隔下得到的序列其可预报性是否会受到影响；

（2）插值问题。对于问题（1）中的不同采样间隔的时间序列，通过插值的方法得到与原始序列同样长度的时间序列，探讨在此情况下序列的可预报期限会有怎样的变化，是否能够得到真实的可预报期限；

（3）插值间隔问题。对于通过采样得到的时间序列，采用不同的插值间隔得到不同长度的序列，其可预报性是否会受到影响？在多大的插值间隔下得到的时间序列的可预报性最能接近真实序列的可预报性？

3结果分析

以下给出对于以上3个问题研究得到的结果。

3.1 不同采样间隔对系统可预报期限估计的影响

对于Lorenz系统，我们以x单变量为例，固定时间步长h=0.01，取序列长度N=1000000，对该时间序列进行不同间隔的采样后得到新序列的平均误差增长曲线如图1所示。可以看到，所有的误差增长曲线的饱和值相同，在采样间隔较小时，所得序列的误差平均增长曲线的初始值也较小，比较接近原始序列的误差平均增长曲线的初始值。随着时间的发展，所得序列的平均误差增长曲线最终缓慢达到饱和。这说明此时找到的相似点之间初始误差较小，基本能满足局地动力相似的要求，此时的误差增长曲线能代表其真实的误差发展情况。随着采样间隔的增大，所得序列的平均误差增长曲线的初始值也越来越大，且随着时间的发展更加迅速地到达误差增长的饱和值。这说明此时寻找到的相似点之间初始误差较大，相对于原始序列的真实局地动力相似点，此时找到的相似点已很难满足

局地动力相似的要求，因此得到的误差发展曲线已不具有能真实地表征序列平均误差增长的情况的能力，已经失去了物理意义。因此在较大的采样间隔的情况下，无法找到真实的局地动力相似，不能得到序列真实的平均误差增长曲线，进而也无法对其可预报期限得到准确估计。结合以上的讨论，这里我们根据误差发展的情况认为可以采用的最大采样间隔为100Δt，即当采样间隔大于该值时，序列无法得到准确的误差平均增长曲线。

图1 Lorenz系统x单变量的误差增长曲线

对于采样间隔小于100Δt的序列，计算了它们的可预报时间，如图2。必须指出的是，不同的采样间隔下得到的误差增长到达误差饱和值的时间需要乘以相应的时间步长才是正确的可预报时间，这里时间步长即为采样间隔。可以看到，插值后所得序列的可预报期限均小于原始序列的可预报期限，且基本上随着采样间隔的增大，所得序列的可预报时间逐渐降低。相对于原始序列接近12的可预报时间，采样间隔在最大为100Δt时得到的可预报时间约为8，与原始序列的可预报时间相比，降低了约三分之一。这说明对于不同的采样间隔，所得序列的可预报期限的估计会受到影响，基本上随着采样间隔的增大，所得序列的可预报期限的估计受到的影响更大，可预报时间逐渐降低。

3.2 插值对系统可预报期限估计的影响

在上一节中讨论了对于不同的采样间隔，所得序列的可预报期限会受到怎样的影响，结果表明对于采样间隔过大的情况，序列无法找到真实的局地动力相似，进而也无法得到准确的误差发展曲线，对其可预报期限的估计则更无从谈起。而对于采样间隔相对较小，所得序列的局地动力相似基本能反映其真实物理意义的情况时，发现其可预报时间随着采样间隔的增大逐渐减小。那么，对于以上这些情况，是否能够通过插值成与原始序列同样长度的序列，来消除采样带来的对其可预报性的影响？这里我们使用三次样条插值来研究这个问题。

图2 Lorenz系统x单变量原始序列的可预报时间（虚线）以及不同采样间隔下序列的可预报时间（实线）

使用三次样条插值方法对不同采样间隔nΔt的序列插值成与原始序列相等长度N=1000000的序列，用非线性局部Lyapunov指数方法计算其误差平均增长情况，如图3所示。可以看到，随着插值后序列其原本的采样间隔的逐渐增大，平均误差增长曲线先是逐渐以更快的速度发展并达到饱和，然而当采样间隔继续增大后，平均误差增长曲线却逐渐降低了增长速度，开始缓慢地达到饱和，甚至在采样间隔为1000Δt时，平均误差增长曲线的速度比原始序列的还要慢，并更慢地达到了饱和值。从对应的

可预报期限的图上可以看到（见图4），随着采样间隔的开始增大，插值后序列的可预报时间迅速减小，当采样间隔为40Δt时，此时插值后序列的可预报时间减小到4左右，当采样间隔进一步增大到50Δt至100Δt时，此时可预报期限维持在较低的值4附近，没有发生大的波动。随着采样间隔的进一步增大，插值后序列的可预报时间迅速增大，到采样间隔为1000Δt时，甚至达到了比原始序列更高的可预报期限。相对于采用不同采样间隔得到的序列计算得到的可预报时间，插值成原始序列长度的做法得到的可预报时间在采样间隔较小时，不能改善不同采样间隔带来的可预报期限降低的影响，反而得到了更低的可预报期限的估计。而对于采样间隔较大的情况，原先的误差平均增长曲线的初始值较大，可预报期限由于不满足真实的局地动力相似无法得到，而插值后得到序列的误差平均增长曲线的初始值与原始序列的非常接近，可预报期限反而随着原先采样间隔的增大而增大，并能得到超过原始可预报期限的估计。

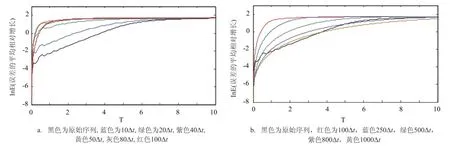
图3 对不同采样间隔的序列插值成与原始序列相同长度后计算的误差平均增长曲线图

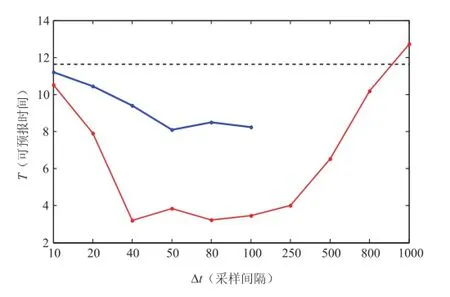
图4 原始序列的可预报时间（虚线），不同采样间隔下序列的可预报时间（蓝线），对不同采样间隔插值后序列的可预报时间（红线）

那么，对于以上情况，是否说明在采样间隔较大的情况下，插值可以改善采样间隔造成的对序列可预报期限估计的影响呢？我们给出对于以上不同采样间隔下，插值成原序列长度的时间序列图，如图5。可以看到，对于采样间隔很小，在10Δt到20Δt时，插值后序列的基本动力特征与原始序列的非常接近，插值所引入的时间序列上的其余的点能够基本保持原始序列的动力特征。同时由于此时较小的采样间隔，对于没有落在真实序列值上的插值点，它们相对于真实采样点来说是较小的一部分，也即信噪比较高，因此此时插值后序列得到的平均误差增长曲线以及可预报期限都与原始序列的较为接近。当采样间隔继续增大，在40Δt到100Δt时，此时插值后序列与原始序列相比只能抓住原始序列的部分动力特征，同时由于采样间隔的增大，信噪比也逐渐降低，因此此时插值后序列得到的平均误差增长曲线更加偏离原始序列的误差增长曲线，且更快速地达到饱和值，因此得到的可预报期限较低。随着采样间隔的进一步增大，在250Δt到1000Δt时，此时插值后序列与原始序列相比仅能表现原始序列的大体趋势，完全无法体现原始序列的基本动力特征，从时间序列上来看近似于做了低通滤波的效果，同时信噪比进一步降低。因此在这种情况下，插值后得到的序列并不能体现原

始动力系统的动力特征，其性质已发生改变，此时得到误差平均增长曲线的初始误差值明显接近于原始序列的误差增长曲线的初始误差值，误差平均增长曲线也越来越靠近原始序列的，因此得到了越来越高的可预报期限的估计。

由以上分析可以发现，将不同采样间隔的时间序列插值成与原始序列同样长度的时间序列，在采样间隔较小的情况下，如小于100Δt时，并不能改善由于采样带来的可预报期限降低的影响，反而会更加降低对序列可预报期限的估计。而在采样间隔较大时，如大于250Δt时，还会由于插值导致序列的动力特征发生变化，使得插值序列与原始序列的值相差更大，得到虚假的误差增长曲线和可预报时间。

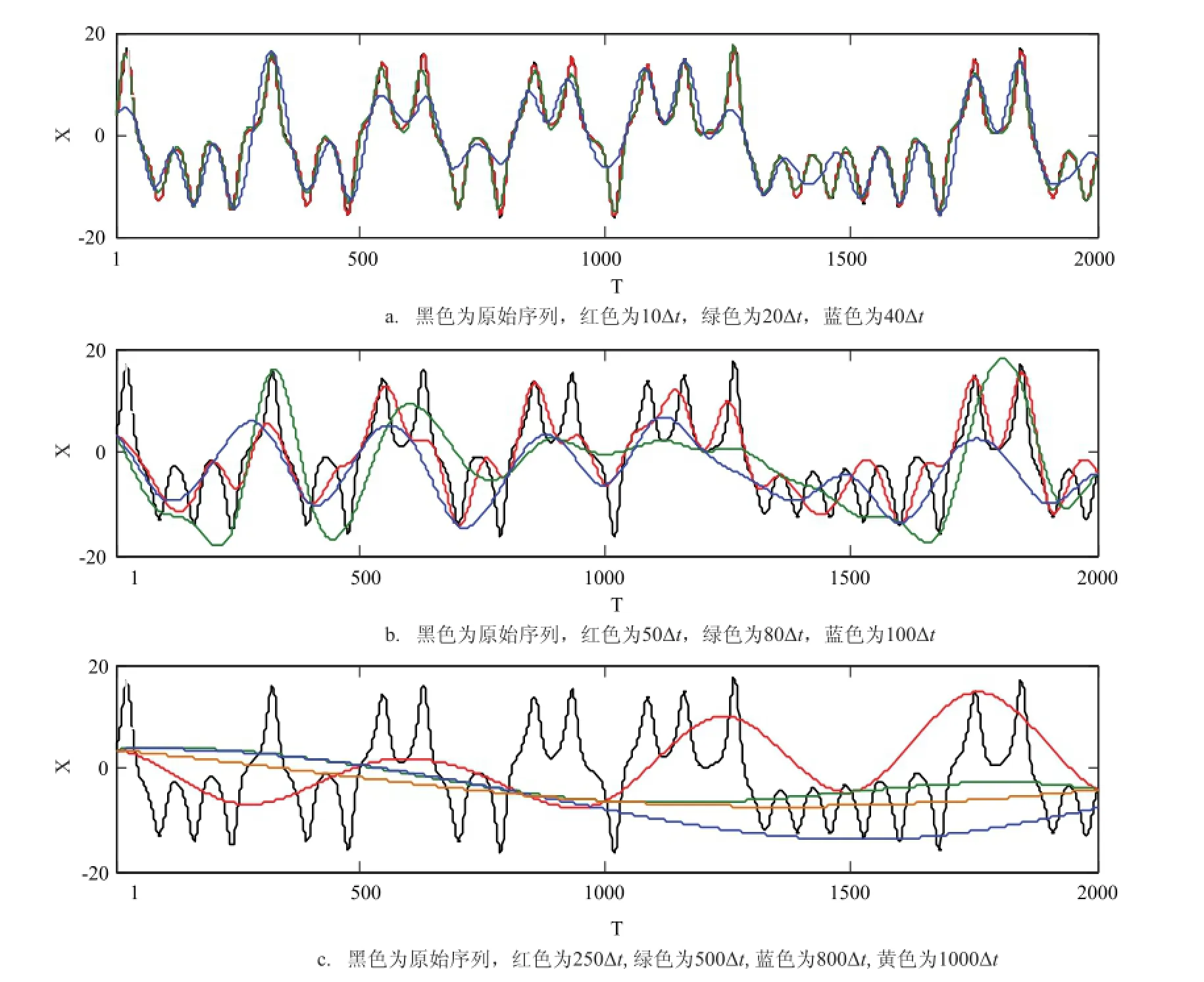
图5 Lorenz系统x单变量在不同采样间隔下插值后的时间序列图

3.3 不同插值间隔对系统可预报期限估计的影响

上一节的分析表明，将不同采样间隔的时间序列插值成与原始序列同样长度的时间序列并不能改善对其可预报期限的估计，甚至会造成虚假结果。那么，当采样间隔相对较小时，使用不同的插值间隔，是否能改善对系统可预报期限的估计呢？根据以上的分析，这里我们选用采样间隔为100Δt的序列作为试验数据，探讨它在不同插值间隔下，可预报性会有怎样的变化。

将对原序列通过采样间隔为100Δt提取出来的新序列，应用三次样条函数，等距地插值成不同长度的序列。具体做法是通过三次样条函数将原序列相邻两点之间插值生成不同个数的点，如插值生成1个点，2个点，3个点，4个点，5个点，9个点，19个点，39个点，49个点，99个点。其中当给定序列的相邻两点之间插入生成点的个数为99个时，即为上节中所讨论的插值成原序列长度的情况。图6给出了以上这些情况下序列的平均误差发展曲线，可以看到，随着插值点数的增多，误差平均增长曲线的

初始值越来越靠近原始序列的误差平均增长曲线的初始值。这表明寻找到的局地动力相似点之间的初始误差随着插值点数的增多而逐渐增大。计算这些情况下的可预报时间，如图7所示。可以看到，在对采样序列相邻两点之间只插值生成1个点时，序列的可预报期限约为6，与原始序列的接近12的可预报期限相比，小了一半。与直接采样得到的序列其可预报期限为8相比，也减小了2。随着插值点数的增多，序列的可预报期限继续降低，当插值点数大于3个点后，基本上系统的可预报期限稳定在4附近，可预报期限不再随插值点数的增多而发生明显变化。这说明采用不同的插值个数并不能改善并提高对系统可预报期限的估计，随着插值个数的增多，系统的可预报期限的估计反而更低。这可能是由于插值过多的点数引入了较多的虚假信息，干扰了系统真实的动力特征，因此也影响了寻找到真实的局地动力相似，降低了对系统可预报期限的估计。

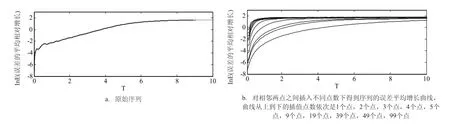
图6 Lorenz系统x单变量采样间隔在100Δt时所得序列在插值不同点数后的误差平均增长曲线图

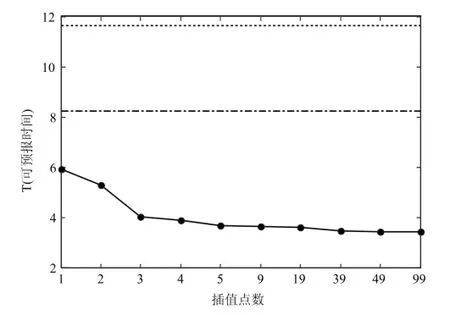
图7 Lorenz系统x单变量原始序列的可预报时间（虚线），采样间隔100Δt时序列的可预报时间（点划线），相邻两点间插值不同的点数的序列的可预报时间（实点线）

4总结

本章利用NLLE方法来研究了采样和插值对混沌系统可预报性的影响的问题，主要结论如下：

（1）对于不同的采样间隔下得到的时间序列，其可预报性会受到不同采样间隔的影响。当采样间隔相对较小时，所得序列的局地动力相似基本能反映其真实物理意义，其可预报时间随着采样间隔的增大逐渐减小。当采样间隔较大时，所得序列已不能找到真实的局地动力相似，无法得到其真实的误差增长情况，也无法得到可预报期限的估计；

（2）将不同采样间隔的时间序列插值成与原始序列同样长度的时间序列，在采样间隔较小的情况下，并不能改善由于采样带来的可预报期限降低的影响，反而会更加降低对序列可预报期限的估计。而在采样间隔较大时，还会由于插值导致序列的动力特征发生变化，使得插值序列与原始序列的值相差更大，得到虚假的误差增长曲线和可预报时间；

（3）采用不同的插值个数并不能改善并提高对系统可预报期限的估计，随着插值个数的增多，系统的可预报期限的估计反而更低。这可能是由于插值过多的点数引入了较多的虚假信息，干扰了系统真实的动力特征，因此也影响了寻找到真实的局地动力相似，降低了对系统可预报期限的估计。

在实际情况中，随着现代海洋观测技术的不断

提升，一部分海洋观测资料的时间分辨率较高，可以利用的资料长度较长，当我们直接对其应用NLLE方法来研究其可预报性时，就能得到较为接近真实的可预报期限的估计。而当使用一些观测间隔较长、资料长度较短的物理量资料来估计其可预报期限时，可能其无法满足局地动力相似的特征，当对其采用插值的方法增加数据长度时，所得可预报期限的估计可能就会不够准确。这提示我们在利用实际海洋观测资料估计其可预报期限时，选用较高分辨率较长时间序列的资料可以得到更接近真实的可预报期限。

[1]Lorenz E N.Deterministic nonperiodic flow[J].Journal of the A tmospheric Sciences,1963,20(2):130-141.

[2]丑纪范.大气动力学的新进展[M].兰州:兰州大学出版社,1990; 1-214.

[3]罗哲贤.热带气旋异常运动可预报性问题的理论研究[J].气象, 1994,20(12):39-41.

[4]段晚锁,穆穆.非线性优化方法在大气和海洋科学数值研究中的若干应用[J].应用数学和力学,2005,26(5):585-594.

[5]Mooers C N K.Coastal ocean prediction[M].Washington,DC: American GeophysicalUnion,1999:1-523.

[6]Pinardi N,Woods JD.Ocean forecasting:conceptual basis and applications[M].New York:Springer Verlag,2002:472.

[7]Mu M,Duan W S,Chou J F.Recent advances in predictability studies in China(1999-2002)[J].Advances in Atmospheric Sciences, 2004,21(3):437-443.

[8]王辉,刘娜,李本霞,等.海洋可预报性和集合预报研究综述[J].地球科学进展,2014,29(11):1212-1225.

[9]Li JP,Ding RQ.Temporal-spatialdistribution of the predictability limit ofmonthly sea surface temperature in the global oceans[J]. International Journalof C limatology,2013,33(8):1936-1947.

[10]May R M.Simple mathematicalmodels w ith very complicated dynam ics[J].Nature,1976,261(5560):459-467.

[11]Palmer T N.A nonlinear dynamical perspective on climate prediction[J].Journalof Climate,1999,12(2):575-591.

[12]段晚锁,穆穆.用非线性最优化方法研究El Niño可预报性的进展与前瞻[J].大气科学,2006,30(5):759-766.

[13]Eckmann J P,Ruelle D.Ergodic theory of chaos and strange attractors[J].Review sof Modern Physics,1985,57(3):617-656.

[14]Fraedrich K.Estimating weather and climate predictability on attractors[J].Journal of the A tmospheric Sciences,1987,44(4): 722-728.

[15]Fraedrich K.1988.El Niño/Southern Oscillation predictability[J]. M onthlyWeather Review,1988,116:1001-1012.

[16]Lacarra J F,O Talagrand.Short-range evolution of small perturbations in a barotropic model[J].Tellus,1988,40A(2): 81-95.

[17]Mu M.Nonlinear singular vectors and nonlinear singular values [J].Science in China Series D:Earth Sciences,2000,43(4): 375-385.

[18]Ding R Q,Li JP.Nonlinear finite-time Lyapunov exponent and predictability[J].Physics LettersA,2007,364(5):396-400.

[19]李建平,丁瑞强,陈宝花.大气可预报性研究的回顾与展望[C]// 21世纪初大气科学前沿与展望—第四次全国大气科学前沿学科研讨会论文集.北京:气象出版社,2006:96-104.

[20]丁瑞强,李建平.混沌系统可预报期限随初始误差变化规律研究[J].物理学报,2008,57(12):7494-7499.

[21]Ding R Q,Li JP,Ha K J.2008.Trends and interdecadal changes of weather predictability during 1950s-1990s[J].Journal of GeophysicalResearch,2008,113(D24):D24112.

[22]丁瑞强,李建平.非线性误差增长理论在大气可预报性中的应用[J].气象学报,2009,67(2):241-249.

[23]李建平,丁瑞强.混沌系统单变量可预报性研究[J].大气科学, 2009,33(3):551-556.

[24]王革丽,杨培才,吕达仁.场时间序列预测方法及其预测能力的试验分析[J].大气科学,2004,28(4):536-544.

[25]彭波,郭树祥,赵晨曦.高分辨率资料处理[J].勘探地球物理进展,2004,27(6):415-421.

[26]熊安元,王颖.气候平均值和方差的次序统计估计量[J].南京气象学院学报,2007,30(5):694-698.

[27]史珍,丁瑞强,李建平.随机误差对混沌系统可预报性的影响[J].大气科学,2012,36(3):458-470.

Im pactsof sam p ling intervaland interpolation on theestim atimation of the predictability of chaotic system s

SHIZhen1,2,DINGRui-qiang3,LIJian-ping4,5,WANG Zhang-gui2
(1.Schoo lofPhysics,PeKing University,Beijing 100871 China;2.Key Laboratory ofResearch on Marine Hazards Forecasting,NationalMarine Environmental Forecasting Center,Beijing 100081China;3.State Key Laboratory ofNumericalModeling forAtmospheric Sciencesand Geophysical Fluid Dynamics,Institute ofAtmospheric Physics,Chinese Academy ofSciences,Beijing 100029China;4.College ofGlobalChange and Earth System Sciences,Beijing Normal University,Beijing 100875 China;5.JointCenter for Global Change Studies,Beijing 100875China)

Based on the nonlinear local Lyapunov exponent(NLLE)approach,the influencesof sampling interval and interpolation on the predictability of the Lorenz system are studied.The results show that the impacts of the sampling interval on the predictability of the chaotic system can be reduced gradually w ith the increase of the sampling interval in certain extent.But when the sampling interval exceeds a certain value,the real local dynam ical sim ilarity cannot be found in the resultant sequence.Thus the real error grow th and the accurate estimate of the predictability lim it of the chaotic system cannot be obtained.The present study also attempts to reconstruct the time series by using the interpolation method.However,the findings indicate that interpolation cannoteffectively improve the estimate of the predictability lim itof chaotic systemswhether in larger or smaller sampling interval.In addition,w ith the increase of the number of interpolation,the estimate of the predictability lim itof chaotic systems can be lower.These resultssuggest thatdataw ith higher resolution and longer time series can be obtainedmore close to the realpredictability lim it.

nonlinear local Lyapunov exponent;predictability;chaotic systems

P732.4

A

1003-0239（2015）06-0066-08

2015-10-02

国家自然科学青年基金（41306008）；国家自然科学面上基金（41376016）

史珍（1984-），女，助理研究员，博士，大气和海洋可预报性研究。E-mail：shiz@nmefc.gov.cn

10.11737/j.issn.1003-0239.2015.06.009