泥料在啮合异向双螺杆不同转速下挤出过程的数值模拟

曹新林，何家波，张柏清

（1. 漳州职业技术学院，福建 漳州 363000； 2.浙江大学，浙江 杭州 310027；3.景德镇陶瓷学院，江西 景德镇 333403）

泥料在啮合异向双螺杆不同转速下挤出过程的数值模拟

曹新林1，何家波2，张柏清3

（1. 漳州职业技术学院，福建 漳州 363000； 2.浙江大学，浙江 杭州 310027；3.景德镇陶瓷学院，江西 景德镇 333403）

本文简要介绍泥料双螺杆元件的有限元模型的网格划分，阐述了泥料在啮合异向双螺杆挤出机中的速度和压力边界条件。说明了在螺杆转速不同的前提下，通过数值模拟分析，得出泥料在啮合异向双螺杆挤出机中的速度和压力变化情况。

泥料；双螺杆挤出机；数值模拟

0 引 言

用于生产制备陶瓷泥料的主要设备是真空练泥机，影响泥段挤出质量的关键在于其挤出部分。然而长期以来，我国对泥料挤出机的研究以单轴为主，双轴和三轴的研究相对较少，所以加强双螺杆泥料挤出机的相关研究对提高泥条挤出质量和效率具有重大的意义。

国内外对双螺杆挤出机挤出过程都进行了相关模拟研究。意大利的Antonio Ficarella等利用流体动力学数值模拟模型，对聚合物在同向双螺杆挤出机的挤出过程进行了数值模拟计算，在改变温度、压力、螺杆转速等条件下，对剪切速率、停留时间分布等流体动力学变量进行了测定[1]。Machado.A .V等对同向双螺杆挤出机中物料流动的相关理论进行了分析，阐述了物料流型、混合效果和停留时间分布特点[2]。Fukuoka等对双螺杆挤出机进行数值模拟分析，建立了数学模型，并通过仿真来验证模型的正确性[3]。刘芳采用Polyflow流场计算软件对五种新型啮合异向非常规螺杆元件在熔体输送段的非牛顿流场进行了三维等温模拟，得到五种元件的流量、平均剪切应力等[4]。

通信联系人：曹新林(1965-)，男，副教授。

1 泥料双螺杆元件的有限元模型

为了能够更好地分析泥料在啮合异向双螺杆挤出机中的运动挤出过程，这里不讨论如何在Pro/E中构造双螺杆的三维几何模型，主要考虑将三维模型导入到ANSYS软件中进行有限元分析过程。

1.1 有限元模型的建立

由于Pro/E与ANSYS数据对接方便，只需在Pro/E中将已经建好的模型保存为ANSYS能够识别的标准图形文件(如IGES)，然后打开ANSYS软件使用File→Import导入模型即可。将Pro/E中的三维模型导入到ANSYS 10.0中，得到了泥料双螺杆挤出机螺杆元件的有限元模型如图1所示。

Correspondent author:CAO Xinlin(1965-), male, Associate professor.

E-mail:caoxinlin85@163.com

1.2 网格划分

根据《有限元法基础》[5]：对于有限元模型来说，网格划分越细，单元个数越多，计算结果就越准确。本研究利用ANSYS软件的FLOTRAN模块并选择3D FLUID142单元作为流场分析基础。选用自由网格(Free)划分法及图2 所示的四节点四面体单元形状进行网格划分，共划分出103075个单元和24764个节点，网格划分后有限元模型如图3所示。

2 边界条件的确定

图1 有限元模型Fig.1 Finite element model

图2 四节点四面体单元Fig.2 Four-node tetrahedral element

图3 网格划分模型Fig.3 Mesh model

采用与泥料真空挤出机实际工况一致的“动绞刀、静筒壁”的假设[6]来确定边界条件，由于是静筒壁，所以只需考虑螺旋绞刀的速度即可。

因为螺旋绞刀面是移动壁面，壁面将“牵引”流体移动，垂直于壁面的速度分量为零。螺旋绞刀面上各点的速度随其在绞刀面位置的变化而不同，其切向速度VR为：

其中：Rf表示泥料所在位置半径；VR表示Rf处的切向速度，y表示泥料所在位置的径向高度且0≤y≤(R1-R2)，R1是绞刀半径，R2是轴毂半径。

通过实测可得，泥料密度为ρ=1.905 g/ml，屈服极限为fv=10180 Pa，牛顿粘度为ηN=1090 Pa·s，塑性粘度为ηS=1090 Pa·s，表观粘度为ηB=2370 Pa·s[7]。假设在理想状态下泥料具有最大运动速度的地方是螺旋绞刀顶部，取螺旋绞刀的转速为n=80 r/min，代入下面公式可得螺旋绞刀的角速度及最大线速度分别为：

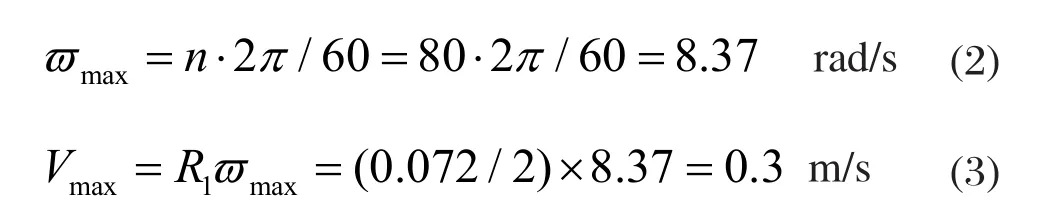
式中： n为螺旋绞刀转速；ϖmax为绞刀角速度； Vmax为绞刀最大线速度。

对于泥料在双螺杆挤出机中的内流问题，令流场特征长度L为其水力直径，可得其特征长度：

其中A表示泥料截面积，C表示湿周长度。将L代入以下公式，得到最大雷诺数：

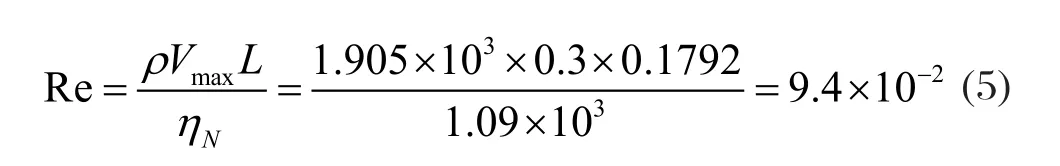
因为得到的最大雷诺数远小于层流的临界雷诺数2000，所以泥料在啮合异向双螺杆挤出机螺槽中的流动属于层流流动，只分析层流情况即可。

3 不同螺杆转速下的数值模拟

在保证泥料的各项物理属性及螺杆元件的几何参数不变的前提下，选取入口压力为0 MPa，出口压力为0.1MPa。改变螺旋绞刀(螺杆)的转速，在ANSYS中设定各项边界条件，进行数值模拟得到泥料在啮合异向双螺杆挤出机中的速度和压力变化情况如下。

3.1 螺杆转速n取值50、60、70、80 r/min的速度图

(1)X方向速度见图4、图5、图6、图7。

由图4、图5、图6、图7分析可得：随着螺杆转速的增大，泥料在螺旋绞刀外缘上的相对速度比在轴毂上更大。但泥料在铰刀上的X方向速度分量最大值是先增后减，这是因为泥料在双螺杆流道中受到牵引力和剪切力的共同作用。

(2)Y方向速度见图8、图9、图10、图11。

根据以上四图可以看出：随着螺杆转速的增加，泥料在铰刀上的Y方向速度分量最大值呈现降-增-降的状态。这是因为机筒与螺杆之间有一定的间隙，产生了泥料回流，影响了泥料在Y方向的速度变化。

(3)Z方向速度见图12、图13、图14、图15。

图4 n=50 r/minFig. 4 n=50 r/min

图5 n=60 r/minFig. 5 n=60 r/min

图6 n=70 r/minFig. 6 n=70 r/min

图7 n=80 r/minFig. 7 n=80 r/min

图8 n=50 r/minFig.8 n=50 r/min

图9 n=60 r/minFig.9 n=60 r/min

图10 n=70 r/minFig.10 n=70 r/min

图11 n=80 r/minFig.11 n=80 r/min

图12 n=50 r/minFig.12 n=50 r/min

图13 n=60 r/minFig.13 n=60 r/min

图14 n=70 r/minFig.14 n=70 r/min

图15 n=80 r/minFig.15 n=80 r/min

图16 n=50 r/minFig.16 n=50 r/min

图17 n=60 r/minFig.17 n=60 r/min

分析以上四图可知：随着螺杆转速的增大，泥料在铰刀上的Z方向速度分量最大值是一直增大的，说明泥料受到螺杆Z方向的牵引力比较大。但在转速达到80 r/min时由于转速过大使得泥料发热，泥料的粘性力和屈服应力发生改变导致泥料在Z方向速度突降。

图18 n=70 r/minFig.18 n=70 r/min

图19 n=80 r/minFig.19 n=80 r/min

3.2 螺杆转速n取值50、60、70、80 r/min的压力图

通过对比分析以上四图可知：泥料在啮合异向双螺杆挤出机中入口处所受压力值很小，在出口处所受压力值达到最大。随着螺杆转速的增加，压力值同比增加更快，这样有助于使泥料在挤出过程中变得更密实，提高了泥条质量和出泥率。

4 小 结

在保证其它边界条件固定的前提下，改变螺杆转速对泥料在双螺杆挤出机螺杆流道中的速度、压力分布情况进行数值模拟。由数值模拟分析结果可知：

随着螺杆转速的增大，泥料在螺旋绞刀外缘上的相对速度比在轴毂上更大，但是由于受到各种影响（如泥料回流，牵引力作用等），使其在螺旋绞刀外缘上的整体速度无法呈现一直增长的状态。

随着螺杆转速的增大，泥料在啮合异向双螺杆挤出机中的所受压力值从入口到出口的增加速率变大，并在出口处达到最大值，这样有助于形成致密度高的泥段，同时缩短了泥条的生产周期。

[1] FICARELLA A, MILANESE M, LAFORGIA D. Numerical study of the extrusion process in cereals production: Part II. Analysis of variance [J]. Journal of Food Engineering, 2006, 72(11): 179-188

[2] MACHADO A V, COVAS J A, VAN DUIN M. Evolution of morphology and of chemical conversion along the screw in a co-rotating twin-screw extruder [J]. Journal of Applied Polymer Science, 1999, 71(1): 135-141

[3] TAKAMASA F. Numerical analysis of a reactive extrusion process: Part II. Simulations and verifications for the twin screw extrusion [J]. Polymer Engineering and Science, 2000, 12(5): 40-42

[4] 刘芳. 基于三次准均匀B样条理论的异向双螺杆元件设计新方法的研究与开发[D]. 北京: 北京化工大学, 2005.

[5]蒋友凉. 有限元法基础[M].北京:国防工业出版社,1980

[6] 张柏清, 裴佳宏, 汤兴国, 等. 真空练泥机中陶瓷泥料挤出过程的研究[J].中国陶瓷工业, 2004, 11(3): 11-13.

ZHANG Baiqing, et al. China Ceramic Industry, 2004, 11(3): 11-13.

[7]陈惠钊. 粘度测量[M]. 北京:中国计量出版社, 2003.

Numerical Simulation of Ceramic Paste Extrusion in Anisotropy Intermeshing Twin Screw Extruder Rotating at Different Speeds

CAO Xinlin1, HE Jiabo2, ZHANG Baiqing3
(1. Zhangzhou Institute of Technology, Zhangzhou 363000, Fujian, China; 2. Zhejiang University, Hangzhou 310027, Zhejiang, China; 3. Jingdezhen Ceramic Institute, Jingdezhen 333403, Jiangxi, China)

The paper briefly introduced the grid division of finite element model of twin screw element for ceramic paste and elaborated the ceramic paste’s velocity and pressure boundary conditions in the anisotropy intermeshing twin screw extruder. Then, the variation of ceramic paste’s velocity and pressure in the anisotropy intermeshing twin screw extruder rotating at different speeds was observed through the numerical simulation.

ceramic paste; twin screw extruder; numerical simulation

date: 2015-06-19. Revised date: 2015-09-20.

10.13957/j.cnki.tcxb.2015.06.019

TQ174.6

A

1000-2278(2015)06-0678-05

2015-06-19。

2015-09-20。