基于GA+ACO的交通拥挤及事故规避系统研究

陆文昌++邓傲++袁朝春++陈龙

摘 要：为了减少车辆在行驶过程中产生的交通事故和规避拥挤道路，研究了道路拥挤程度的影响因素和评价指标以及道路事故的理论与模型。提出采用路网的动态路阻对事故的影响程度和道路拥挤程度进行综合评价，并对动态路阻采用模糊理论进行量化。同时研究了遗传算法和蚁群算法在该规避系统中的应用，采用遗传蚁群的混合算法，综合了遗传算法全局搜索和蚁群算法求解精确的特点。用Matlab对该路阻函数和混合算法进行仿真，并进行了实际路网测试，结果表明利用该路阻函数和混合算法能够达到规避拥挤、规避潜在事故和规避已发事故的目的。

关键词：交通路网；遗传蚁群混合算法；道路拥挤；最优路径；事故阻断

中图分类号：U461.91文献标文献标识码：A文献标DOI：10.3969/j.issn.2095-1469.2015.05.10

随着社会经济的飞速发展，我国的汽车保有量也逐年提高，造成道路交通承载压力越来越大，导致大量的交通拥挤和交通事故。所以道路交通的拥挤程度评价和交通事故的预测规避对交通规划以及道路交通安全控制等具有重要意义。交通拥挤程度评价系统的核心在于动态路阻的计算和最小拥挤路径的求解。国内外对于交通拥挤进行了多方面的研究，在动态路阻的计算与评价方面主要有层次分析法、模糊综合法、主成分分析法等[1]。最小拥挤路径的求解算法经典的有Dijkstra、Floyd、A*算法以及它们相应的改进算法等[2]。仿生智能路径优化算法是针对实际路网的复杂性以及用传统方法求解优化问题存在很多困难的情况而发展起来的。目前国内外研究热门的智能路径优化算法主要有遗传算法、粒子群优化算法以及蚁群算法等[3]。

交通事故的预测是道路安全评价、规划以及决策的基础，其预测模型主要有回归模型法、经验模型法、时间序列法等[4]。国内外大多数论文一般将拥挤评价和事故预测规避分开，然而两者间互相有很深的联系，事故的发生会导致拥挤程度的快速增长，拥挤程度也会导致潜在事故概率的变化。考虑到道路交通各影响因素内部关系的错综复杂性和价值系统的模糊性，对模糊理论进行了相关研究，利用模糊综合法设计了一种路阻的动态计算模型。将道路的拥挤情况和事故链结合综合评价，然后利用遗传与蚁群混合算法，综合遗传算法的全局搜索能力和蚁群算法的快速精确性，进而求解得到最优路径，达到规避拥挤、规避潜在事故和规避已发事故的目的。

1 路网的数学模型

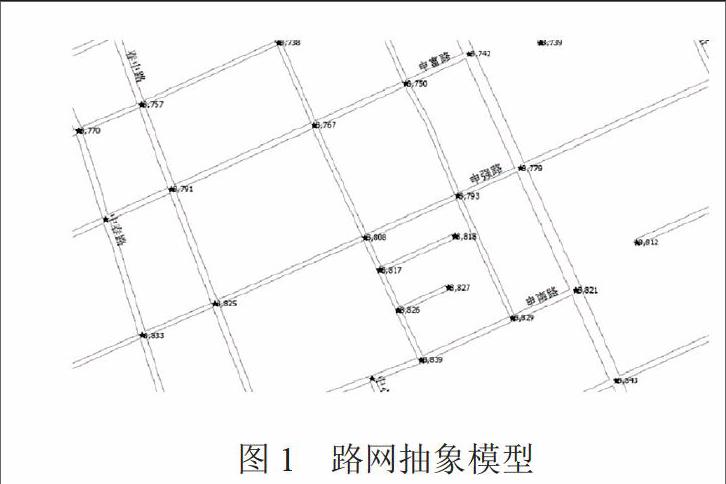
为了迅速、准确而安全地到达目的地，车辆行驶过程中，就要有效地避开拥挤路段和潜在风险事故大的路段或已发生事故的路段，即在起点与终点间寻找一条综合了道路拥挤与事故概率后的最优路径。为了解决上述问题，以结构直观的交通网路图（图1

为用Mapbasic语言编程后，得到的路网抽象模型）为基础，将最优路径的寻找转换成在有向赋权图上求解两点间最短距离的问题。这里的有向赋权图是这样来建立的，即用道路的交叉口或者道路特性（道路宽度、等级）发生改变的位置对应图的节点，两交叉口之间的路段对应图中的边，路段的长度作为该边的权值。这样的赋权有向图用下述公式表示为

。

式中，G为表示路网的赋权有向图；

为路网节点集合；n为路网节点数；E为路网边集合；m为路网边数；D为路网的路权矩阵；dij为i、j两节点间的道路长度，m。根据不同的优化目标，可以定义相应的路权，反映到赋权有向图上，就是各条边的权。本文将其它的影响因素量化为道路的长度，即选取行驶距离为优化目标。设D（t）为路网的动态路阻矩阵，则t时刻相邻2节点i到j的路阻可以简单地表示为Dij（t）=λdij。

2 动态路阻的计算

2.1 动态路阻影响因数的选取

路阻影响因数主要包含两大类：道路属性（宽度、道路等级、交通限制）和交通参数（交通流量、速度、道路占有率、路口排队长度等）。各个因数的影响大小不一样，数据的获得也存在着难易程度上的差别。高速公路或者城市快速路具有典型的连续交通流特征，在上面行驶的车辆可以在相当长的路段上不受其它道路交通流的影响而连续运行，且不会发生因红绿灯而引起的交通拥挤现象。行驶于城市快速路和高速路上的车辆所形成的交通拥挤除了环境因素外，往往是因交通流量过大而造成的。

所以对于高速公路或者城市快速路，选取平均行程速度和交通流量[3，5]。对城市道路而言，其具有典型的间断交通流特征，选取平均行程速度、饱和度S=V/C、平均延误时间[3，6-7]。其中V为进口车道实际交通量，辆/h；C为进口车道通行能力，辆/h。

2.2 动态路阻选取因数的量化[3]

动态路阻矩阵Dij（t）=λdij 。

式中，。

其中λ1为道路属性信息相关的路权系数；λ2为实时交通信息相关的路权系数；λ3为与驾驶者特殊要求相关的路权系数；λ4为与安全相关的路权系数；1为道路长度系数。

（1）λ1取值

λ1=1/GW。G为道路等级，我国将道路分为四个等级：1， 2， 3， 4，数字越大道路越差；W为道路宽度，m。

（2）λ2取值

λ1是动态路阻模型的核心之一，用于表征实时交通信息对拥挤程度的影响，其取值范围为0～1，与相对应道路的拥挤程度成正比关系。λ2的获取步骤如下：

①根据交通流的特性分类，即分成连续交通流和间断交通流。

②根据不同的交通流参考国内外的评价标准，对连续交通流和间断交通流进行拥挤程度的评价。

③利用模糊理论将评价的拥挤程度量化成0～1间可计算的数值。

对高速公路和城市快速路，影响因数为平均行程速度和交通流量。以下各表是由我国采用的《城市交通管理评价指标体系》，我国交通发展研究中心的《交通拥堵评价研究报告》和相关理论研究[7-8]制定。

模糊控制量化步骤：

①选择模糊控制变量，具体见2.1节。

②对输入输出变量的模糊分割。

③选择合适的隶属度函数，所选择的隶属度函数为梯形隶属度函数，其具有计算简单、使用方便的特点。

④根据相关资料和经验确定控制规则。

⑤获取输出曲面。

对连续交通流按照上述步骤获取的输出曲面如图2所示。

城市道路属于间断交通流，选取的参数为饱和度、平均行程速度和平均延误时间。

同理，利用模糊控制的步骤可得当横坐标为平均行程速度，纵坐标为平均延误时间时的输出曲面，如图3所示。

（3）λ3取值

取值为0和0.5，当高速优先时，对高速公路路阻取0，普通道路取0.5，反之分别取0.5和0。驾驶若无特殊要求取值都为0。

（4）λ4取值

事故评价同λ2，分为连续交通流和间断交通流。对连续交通流，由镇江市历年交通事故分析和相关文献[3，9]选取平均行程速度、行车间距、交通流量和货车超载比例。对间断交通流选取平均行程速度、行车间距、交通流量和信号交叉口违规概率。

连续交通流λ4，隶属度函数采用高斯函数，利用重心法反模糊化，输出曲面如图4所示。同理，间断交通流输出曲面如图5所示。

然后我们可以根据实时接收到的车速、流量等数据得到某时刻的λ2、λ4值。

（5）β的取值

令β[β1， β2， β3]，则β为权向量。采用AHP法确定其权重。构造判断矩阵为，则A的最大特征根为3.009 2，检验指标RI0.009 2/0.580.016<0.1，且β（0.16， 0.30， 0.54）。故可以加权实时的λ值，进而得到实时的动态路阻矩阵。特殊地，当λ21时（表示某段道路因发生事故或其它情况完全堵塞）或当λ41时（表示某段道路非常危险，有很大概率发生交通事故），此时β2或β3取无穷（具体取999 999代替）。

3 最优路径的计算

遗传算法在搜索初期具有较高的向最优解收敛的速度，但之后求最优解的速率显著下降。而蚁群算法在搜索的初期由于缺乏信息素，搜索速度缓慢，但当信息素积累到一定强度之后，向最优解收敛的速度就会迅速提高[10-11]。综合两种算法的特点，采用遗传-蚁群混合算法对最优路径进行计算。

3.1 遗传算法与蚁群算法的融合

本文遗传算法与蚁群算法的融合主要体现在两个方面，一是算法初期利用遗传算法的特点快速计算出多组优化解，然后蚁群算法根据这些优化解生成初始的信息素分布，从而弥补蚁群算法初期搜索速度缓慢的不足；二是在利用蚁群算法求解时，为了避免算法过早地陷入局部最优解同时增加求解准确率，利用遗传操作作用于蚂蚁的解分布，增加种群搜索的多样性，从而较高概率地搜索获得问题最优解。其算法流程图如图6所示。

3.2 遗传算法生成信息素的初始分布

3.2.1 编码

本文采用的方式为符号编码，即用实数编号表示节点，然后用这些编号作为一种编码形式参与遗传操作，该编码方法不仅易于遗传操作，而且可以简化优化程序，并可以保证搜索到全局最优解可能存在的整个空间[7]。

3.2.2 种群

种群包含种群的规模和产生初始种群的方法。本文初始种群采用完全随机的方式，即先随机产生染色体。染色体的第一个基因就是起点，第二个基因是从与起点连接的其它节点中随机选择的，重复进行这个过程，直到到达终点为止。为了避免产生环路，规定在一条染色体中，当一个基因被选中之后，就给该基因（节点）作个标记，只有没有标记的基因才能被该染色体选中，该条染色体产生完成后标记全部刷新，然后重复第一步，直到产生的染色体数达到初始种群规模的要求（种群规模选择为100）。

3.2.3 遗传操作

（1）选择算子：遗传算法通过选择操作从当前种群中选出优良个体遗传到下一代，体现“优胜劣汰”的原则。目前常用的选择方法有排序选择法、分级选择法和赌盘选择法等。本文选择赌盘选择法，即每个染色体被选中的概率与其适应度值的大小成正比。此处适应度函数为fij（t）1/Dij（t）。与此同时为了解决赌盘选择法容易引起的“早熟”和“收敛停滞”问题，采用最优保存策略，即当前种群中适应度值最大的染色体直接复制进入下一代种群，不对其进行选择、交叉和变异操作。该策略可以加快收敛速度。

（2）交叉算子模仿了自然界有性繁殖的基因重组过程，是遗传算法较其它进化算法的独有特征，主要通过将两个父代个体的部分基因相互替代得到两个新个体。在遗传算法中，交叉算子是产生新个体的主要手段，保证了种群的多样性。本文采取的交叉方法为随机单点交叉。

（3）变异算子是模仿生物由于各种偶然因素引起的基因突变，是遗传算法中产生新个体的辅助方法，可以保持种群的多样性，防止算法陷入局部最优解。变异算子和交叉算子相互配合，共同完成搜索最优解的过程。变异有删除、替代、插入三种方式，由于本文遗传算法主要工作是提供初始的信息素分布，为了节约算法的时间，采用删除和替代两种方式。

3.3 蚁群算法求解最优路径

算法步骤：

（1）参数初始化。将蚂蚁的位置随机分布在节点上，根据遗传算法产生的优化解对节点间的信息素进行分布。

（2）开始循环。对每个蚂蚁，根据概率转移公式由节点i转移到节点j。当i，j都不在禁忌表时概率转移公式为

。

否则为0。为启发函数，取表达式为1/Dij（t）。α是概率转移公式中信息素影响因子，反映了在运动过程中信息素对蚁群择优的作用大小，其值越大蚁群越倾向于已选择的路径，从而易于陷入停滞状态。β则是概率转移公式中的启发式影响因子，体现了算法中蚁群不同于真实蚁群所添加的启发信息的影响大小。

（3）信息素更新，更新公式为

。

式中，。

（0<<1）表示信息素挥发系数，当第k只蚂蚁在本循环中经过i，j时：

。

否则为0。Lk表示第 k只蚂蚁在本次循环中所走过的路径总长度。

（4）得到本次循环的最优路径和次优路径，并且路径间进行交叉和变异操作。

（5）判断是否达到迭代终止条件，此处选为到达一定的迭代次数。

4 仿真分析

4.1 遗传算法对最优路径的计算

采用Matlab对遗传算法进行仿真。

路网图为34个节点的赋权有向图，如图7所示。

用Matlab对遗传算法进行30次仿真。选取种群规模100，交叉率0.9，变异率0.01，找到最优解的概率约为70%，平均时间2.2 s。输出结果如图8所示。

4.2 蚁群算法对最优路径的计算

蚂蚁个数选取100，转移选择因子选0.2，信息素蒸发系数选0.8。其最优解概率约为80%，平均搜索时间为3.0 s。输出结果如图9所示。

4.3 遗传+蚁群混合算法

参数选择同上，使用遗传算法优化初始信息分布和求解过程中的解分布。最优解概率约为96%，平均时间为3.5 s。输出结果如图10所示。

4.4 仿真结果分析

由表3中的仿真结果可以得出，遗传算法在速度上存在优势（高于蚁群算法25%），蚁群算法则在精确度方面表现良好（高于遗传算法13%）。当节点数目较少时，混合算法在精确度方面得到了提高（12%），但速度方面略微下降（-14%）。这是由于在进行蚁群算法时，为进一步提高精确率进行遗传操作增加了一定时间，此时间大于用遗传算法优化蚁群解分布节约的时间，从而得到的结果是最优解概率得到提升，算法时间增加。但当节点数目增加到100时，混合算法在精确度（10%）和时间（15%）上都有所提升，故在节点数目足够多时，混合算法相对于单一的算法，集成了二者的特点。

5 试验测试

考虑到实际项目需求（集成事故预警与事故链阻断系统，本文未涉及），将系统放于车载终端上硬件资源（arm11开发板）可能出现资源不足，故将最优路径的计算放于后台服务器。测试连接原理图如图11所示。

车载端用于人机交互，主要用于数据的传输和地图的显示。车载端为基于安卓的嵌入式ARM板。OBU与RSU为DSRC无线通信模块，OBU用于与RSU的通信，RSU主要用于部分数据的采集工作与通信。后台为一台PC机，主要用于最优路径的计算。

图12为车载端图，车载DSRC（OBU）为方便安装信号天线置于车顶，由于试验条件所限，实时的平均行程速度和流量数据由两辆汽车的数据平均而来。

图13为路侧端，试验时放于路边。实时数据的获取方式如图14所示。

实时数据获取途径如下。

平均行程速度：首先，车载端通过由装于OBD接口的北斗云蓝牙OBD-2模块（图14（b）中左上角白车与右边黑车）获取自车速度，并将自车速度通过图14（a）中的移动RSU（路侧通信单元）和（b）中左上方小红车上的RSU传给后台，后台将车速平均得到近似平均行程速度。

交通流量：RSU的无线范围约为500 m，两台移动RSU和两台固定RSU统计约2 000 m内的车流量，得到近似交通流量。

饱和度：由装于交叉口的两台固定RSU计算饱和度。

行车间距：由4台RSU根据车辆方位近似计算。

信号交叉口违规概率、货车超载比等由历史数据进行近似。

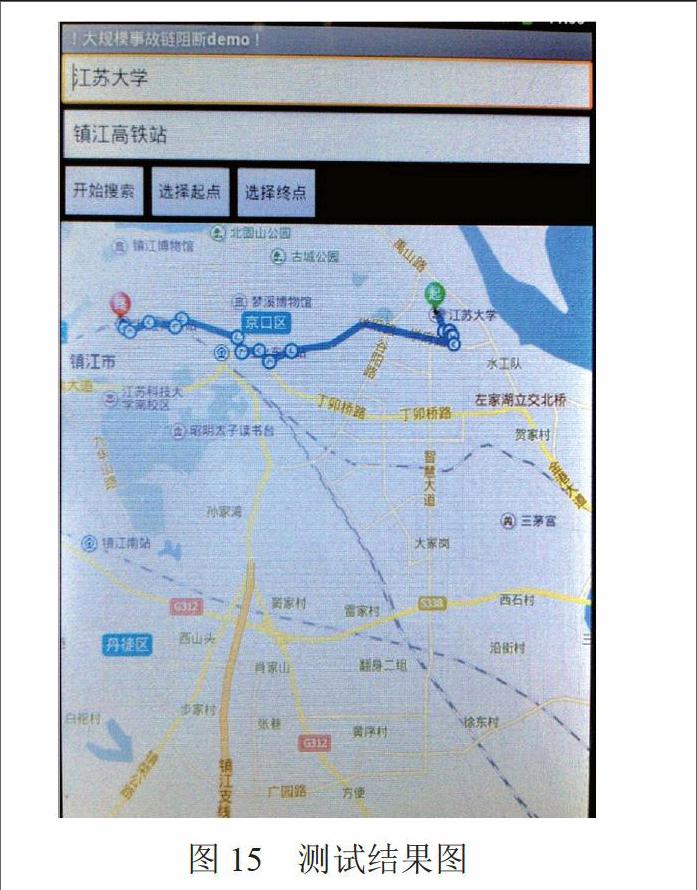
测试结果如图15和图16所示。

测试为在车载端输入起点与终点（移动RSU放于天桥路），然后传给后台。

如图15所示，起点选择为江苏大学，终点选择为镇江高铁站，两点间直线距离为8.2 km，两点间节点数量为67个。显示的最优路径全长10.3 km，计算时间约为5 s，准确率接近100%。对比仿真试验时间略微增加（约1 s左右），经过对比后发现是ARM板与后台的通信过程中耗费了一定的时长。

如图16所示，选定起点与终点后，改变某路段的拥挤度值或安全度值并到达一定阀值，路线会发生相应的改变。为排除规避拥挤、规避已发事故、规避潜在事故间试验的相互影响，测试时选择相同道路（天桥路）进行改变。

由表4和图16可得出，当实时的拥挤状况和安全状况发生改变且到达一定的阀值时，最优路径会发生相应的改变，达到了规避拥挤和规避潜在事故的目的。当标记某段道路为事发路段后，同样可以达到规避已发事故的目的。

6 结论

（1）利用模糊控制对动态路阻进行了量化，采用遗传蚁群的混合算法对最优路径进行求解，并进行了Matlab仿真和实地试验。

（2）仿真结果表明，当节点数目较小时，混合算法在精确度上具有明显优势，但在时间上略微增加。当达到一定的节点数目时，混合算法综合了遗传算法与蚁群算法的优势，在时间和精确度上都有提高。

（3）试验结果表明，使用该模型和算法可以求解得到实时的最优路径，且该路径能达到规避拥挤、规避潜在事故和规避已发事故的目的。

参考文献（References）：

祝付玲， 王炜. 城市道路交通拥堵评价指标体系研究[D]. 南京：东南大学，2006.

Zhu Fuling，Wang Wei. Research on Index of Urban Traffic Congestion Measures [D]. Nanjing：Southeast University， 2006.（in Chinese）

HUANG C J，WANG Y W，CHEN H M，et al. Application of Cellular Automata and Type-2 Fuzzy Logic to Dynamic Vehicle Path Planning [J]. Applied Soft Computing，2014，19（2）：333-342.

李云，谢刚. 基于遗传算法的动态路径优化 [D]. 太原：太原理工大学， 2010.

Li Yun，Xie Gang. Dynamic Path Optimization Based on the Genetic Algorithm [D]. Taiyuan：Taiyuan University of Technology，2010.（in Chinese）

李相勇， 张南， 蒋葛夫. 道路交通事故灰色马尔可夫预测模型 [J]. 公路交通科技，2003（20）：98-100.

Li Xiangyong，Zhang Nan，Jiang Gefu. Grey-Markov Model for Forecasting Road Accidents [J]. Journal of Highway and Transportation Research and Development， 2003（20）：98-100.（in Chinese）

贾顺平，於毅. 城市道路交通状态判别方法研究 [D]. 北京：北京交通大学， 2007.

Jia Shunping，Yu Yi. Research on the Identification Method of Urban Road Traffic Conditions [D]. Beijing：Beijing Jiaotong University，2007.

韩悦臻，曹三鹏. 城市道路交通状态指标体系设计探讨[J]. 公路，2005（6）：121-123.

Han Yuezhen，Cao Sanpeng. Research on the Index System of Urban Road Traffic State [J]. Highway，2005（6）：121-123.（in Chinese）

徐建闽，孙超.城市道路交通状态评价分析研究 [D].广州：华南理工大学，2010.

Xu Jianming，Sun Chao. Research on Urban Traffic Network State Evaluation and Analysis [D]. Guangzhou：South China University of Technology，2010.（in Chinese）

郝媛，徐天东，孙立军. 基于模糊的城市快速路交通流状态判别 [J]. 公路工程，2008，33（2）：94-99.

Hao Yuan，Xu Tiandong，Sun Lijun. Fuzzy Logics Based Traffic State Identification on Urban Expressway [J]. Highway Engineering，2008，33（2）：94-99.（in Chinese）

孟祥海， 郑来， 秦观明. 基于模糊逻辑的交通事故预测及影响因数分析 [J]. 交通运输系统工程与信息， 2009， 9（2）：87-92.

Meng Xianghai，Zheng Lai，Qin Guanming. Traffic Accidents Prediction and Prominent Influencing Factors Analysis Based on Fuzzy Logic [J]. Journal of Transportation Systems Engineering and Information Technology，2009，9（2）：87-92.（in Chinese）

Yu Shiwei，Ding Chang，Zhu Kejun.A Hybrid GA-TS Algorithm for Open Vehicle Routing Optimization of Coal Mines Material [J]. Expert Systems with Applications，2011，38（8）：10568–10573.

?ATAY B. A New Saving-Based Ant Algorithm for the Vehicle Routing Problem with Simultaneous Pickup and Delivery [J]. Expert Systems with Applications，2010，37（10）：6809–6817.