用科学思想指导极限教学

曲峰林+张青

摘要：本文首先从微积分的发展着手分析极限在高等数学教学中的重要性，然后根据科学思想的指导设计教学过程。让学生通过感性认识到理性认识的过程理解极限中的重要思想，体会极限过程中的量变到质变、无限和有限的辩证关系。

关键词：极限;科学思想;高等数学;教学过程

中图分类号：G642.41     文献标志码：A     文章编号：1674-9324（2015）23-0150-02

极限的教学是微积分（高等数学）教学的重要基础，怎样通过课堂教学让学生了解、领会到熟练掌握极限的思想并用于指导学习是我们值得探讨和研究的一个重要问题。高等数学中很多重要的概念都是由极限来定义的，例如微分学中函数连续的概念、导数的定义;积分学中定积分、重积分的定义，等等，都是用极限来定义的。包括级数收敛的定义也是利用了极限的形式给出的。这样看来，极限不仅仅是一个数学概念，也是高等数学中分析问题和解决问题的一个重要的方法，它体现了一种处理客观世界数量变化的新思维、新方法，这个方法与初等数学中的一些技巧和方法有着很大的差别。初等数学是一种以静态的、不变的观点来分析事物的思维方式，而高等数学则是以运动、变化的观点来处理问题和解决问题。在物质世界中，事物的运动是绝对的，静止是相对的，这是物质世界的普遍规律，而极限就是处理变化事物的最有效、最成功的方法之一。然而，从实际教学的情况看来，极限这一章节的教学一直是教学上的难点，学生们初进大学（一般的高等数学课都设置在第一学年），这种从静止不变的思维定式向动态的变化的思维定式的突然转变，一时间很难接受。从数学思想的方面来看，极限思想体现了一些很重要的哲学思想，正确的认识这些思想对于指导教师的教学工作是非常有意义的。同时，能够将这些思想融入教学的过程中，让学生受益是更加重要的事情。笔者从事高等数学的教学工作多年，在这些年的教学工作中，对极限概念的教学有一些心得。下面，我们将从不同的方面加以阐述。

一、从微积分的发展认识极限的作用以指导教学

微积分的创立首先是为了解决17世纪主要的一些科学问题，它们是求运动物体的速度、求曲线的切线、求函数的最大值与最小值以及求曲线的长度这四类典型的问题。随着微积分的概念与技巧的扩展，人们努力想去补充被遗漏了的基础理论。Netwon和Leibniz都尝试解释概念并证明他们的程序是正确的，但他们都没有清楚的理解也没有严密的定义他们的基本概念。其间，包括Taylor、Euler、Lagrange等人，18世纪的几乎每一个数学家都对微积分的逻辑作了一些努力，但多数努力都没有结果[1]。通过对微积分这段发展史看来，认识无穷小和无穷大才是难点之所在，是问题的关键。到了18世纪，达朗贝尔等一些数学家先后明确地表示必须将极限作为微积分的基础概念用以解决微积分理论基础的问题，然而极限概念的第一次比较完整的被阐述是19世纪，法国数学家柯西在《分析教程》中提出：当一个变量逐次所取的值无限趋于一个定值，最终使变量的值和该定值之差要多小就多小，这个定值就叫做所有其他值的极限值，特别地，当一个变量的数值（绝对值）无限地减小使之收敛到极限0，就说这个变量成为无穷小。但柯西的叙述中还存在描述性的词语，如“无限趋近”、“要多小就多小”等，因此还保留着几何和物理的直观痕迹，没有达到彻底严密化的程。直到维尔斯特拉斯提出了极限的静态的定义，排除极限概念中的直观痕迹，给微积分提供了严格的理论基础。由此我们可以看到，直到19世纪以前，微积分的严密化一直未完成。然而用微积分的思想解决问题却推动着很多学科分支的发展。所以，在学生初学高等数学，第一章就要接受极限这个定义方式不同于以往的静态定义，并且极其严密的概念时，可以借助于学生已经建立起来的对图像和函数的直观的概念进行理解。然后再给出精确定义，关于这一点将在下面一个方面里详细叙述。

二、运用从感性认识到理性认识、从特殊到一般的方法设计教学过程

极限的问题主要是无限问题，最难以理解的也是趋于“无穷大”和“无穷小”的这两种提法。用极限的思想解决问题是指把某些实际问题的研究放在无限过程中进行演算，最终得出相应的结论.比如，刘徽的割圆术求圆的面积[2].设有半径为r的圆，利用其内接正n边形的面积A  逼近圆面积S。内接正n边形的面积为：A  =n·  ·sin  ，（n=3，4，5，…）当n无限增大时，A  无限逼近S，或为A  =n·  （2  ·r）·r≈πr  .我们在教授时，要体现随着n的增加，多边形面积接近圆面积的这一现象。笔者认为用数据表格可以很清晰的展现这一过程，如表1（取圆的半径r=1），从表中可以看到正多边形面积越来越接近与圆的面积π，同时还可以发现当边数增加到100以上时，小数点后两位有效数据时与真实值是相等的;边数增加到500以上时，小数点后四位有效数据时与真实值是相等的。即让学生感受到趋近，以及趋近的速度。

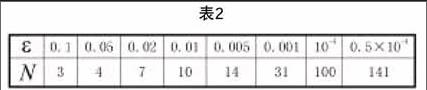
这些直观的数据和生动的例子，可以让学生对于“趋近”这个词有一个感性的认识，并且简单易懂，这是教学的第一个阶段。教学的第二个阶段即为去掉实际的应用背景，用函数和数列的例子，通过观察图形、数据表的方法看到对自变量变化而产生的函数值的变化过程。这时的例子要涵盖自变量趋于无穷时函数值收敛、无穷型发散、振荡的类型;自变量趋于有限常数时函数收敛、发散、间断等类型。尤其要列举出发散的各种情况，因为认识了事物的反面更有助于认识事物的本质含义。教学的第三个阶段即引入极限的精确定义，即ε-N定义和ε-δ定义。然后列举简单的例子进行验证。而验证的过程也建议用表格的形式列出ε，N的取值并且对比图像直观理解趋近的过程。例如：验证

表2列出相应ε，N的取值。

对ε-N定义和ε-δ定义这两个定义的理解是极限教学中的难点，可以说是难点中的难点，教师要认识到难点的关键是什么。笔者通过自身的学习领会和与学生交流看来，无论学生的提问方式是什么样的，他们的关键在于，对这种复杂条件下的定义方式不能正确理解。在初等数学中，定义的模式基本为：若条件P成立，则定义结论A，反之也成立，因为定义为充分必要条件。但极限定义中条件P本身就是一个判断语句，所以教师在教学中应该通过证明极限的存在性，即验证条件;以及利用极限定义证明函数的性质，即利用条件两方面的练习使学生理解这种定义方式。

三、了解极限中体现的哲学思想有助于更好的组织教学语言

从哲学的角度来界定事物发展变化过程中所呈现的无限性是正确理解极限的基础。在这个知识点中，体现的最为显著的就是“量变到质变”的哲学思想。从前面的两个实例看来，第一个例子中，无论边数的取值如何增加，只要是给定的正数，那么计算结果仍然是正多边形的面积，但取极限之后，结果则表示圆的面积。第二个例子中，精确的瞬时速度只能通过缩短时间间隔来近似，时间间隔在实际的操作过程中不可能取为零，但极限运算可以求出最终的极限状态。此外，该定义还体现着“有限和无限的对立统一”。具体说来，无限由有限构成，无限不能脱离有限而独立存在;有限包含无限，有限体现无限。利用有限和无限的这种辩证统一，通过有限认识无限，通过有限去把握无限，通过有限的、相对的各种事物和现象逐步把握事物在无限发展过程中所体现的本质和规律。极限概念这是这种有限与无限的统一，所以能够正确把握无限的内涵，对于组织教学，进而通过课堂的讲授让学生体会有限与无限的辩证关系是学习极限概念重要前提和重要的教学要求。

利用科学的思维指导教学，通过了解历史的发展过程揭示概念的重要本质，科学有效地设计教学过程，能够更好地通过课堂讲授的手段让学生了解、领会到熟练掌握极限的思想并用于指导后面知识的学习是本文研究的重点。在教学改革的过程中，我们利用这个方法进行教学得到的良好的教学效果。所以我们将在此基础上进一步改进这一教学模式，用科学思维、科学的方法指导高等数学的教学。

参考文献：

[1]古今数学思想（第二册）[M].上海科学技术出版社，2002.

[2]极限发展的几个历史阶段[J].高等数学研究，2001，（2）：40-43.endprint