基于“通信原理教学仿真平台”的课程设计
2015-12-07何英庆黄旭方张海龙唐秋玲
何英庆 黄旭方 张海龙 唐秋玲
摘要:针对《通信原理》课程面临的困境,我们课题组开发了一套基于Matlab语言的“通信原理教学辅助软件平台”,该平台集成课程知识要点,提供可视化图形图像,教师可通过演示来帮助讲解,学生也易于理解,同时还可基于软件平台提供的Matlab开放代码,进行课程设计,提高学生的自我学习和动手能力。文中以“DSB的调制和解调”知识点为例,基于软件仿真平台进行课程设计。仿真过程中,按基带调制信号的频谱特性来设计接收端的低通滤波器,通过分析基带信号和已调信号在有无噪声下的时域和频域特性,对通信系统的模拟调制过程有更好地理解。
关键词:通信原理;调制解调;DSB;低通滤波器
中图分类号:G642.0 文献标志码:A 文章编号:1674-9324(2015)26-0130-03
一、“通信原理教学辅助软件平台”介绍
《通信原理》课程理论·性强,数学公式推导多,比较抽象,侧重于对实际通信系统数学模型的研究,而有关通信系统实现的内容,一般只给出系统实现的思路或框图,很少介绍具体实现,与实际的系统实现距离大,从而增加了学生的学习难度。大部分学生在学完本课程之后,并不能对通信原理讲授内容做到深刻的理解,基本上是知其然,但是不知其所以然。这使得学生在将理论知识应用于实践时产生较大困难,如在毕业设计和创新型实践中,学生经常不知如何下手,一片茫然。虽然有相关的辅导资料可以查阅,但本科生的学习任务繁重,自学能力还较差,不能单靠学生努力来改变现状。目前通信原理课程有配套的实验教学内容,但是大部分实验内容还都是在实验箱上进行的。一方面,实验室由于规模的限制,实验设备的台数不多,而招生规模却在不断扩大,学生的实验课时相对有限,所以大部分学生不能得到充分的实践练习和锻炼;另一方面,实验箱平台所支持的实验内容大都是演示性质的,并且实验项目基本固定,学生只能得到对实际通信设备结构、原理的浅显认识,而对通信系统背后的真正工作原理,以及各设备之间的相互关联是片面和模糊的。
针对《通信原理》课程面临的困境,我们课题组开发了一套基于Matlab语言的“通信原理教学仿真平台”,同时编写了“通信原理及仿真实现”教材。图1是软件平台的主界面,图2是该平台集成的课程知识点,图3是第五章内容的主界面,本文的“DSB调制和解调过程分析”就是基于这部分提供的开放代码进行的课程设计。
二、DSB调制解调仿真的基本原理
1.课程设计要求。设消息信号m(t)为:
m(t)=sinc(100t),|t|≤t■ 0 else
其中t■=0.1s。用这个消息来调制载波c(t)=cos(2πfct),f■=250,要求完成以下任务:
(1)写出DSB-SC已调信号的表达式。
(2)画出消息信号和已调信号的时域波形图、频谱图。
(3)将已调信号进行相干解调,画出恢复后消息信号的时域波形、频谱。
(4)假设已调信号叠加的噪声信号,SNR为10dB,进行相干解调后,画出恢复后消息信号的时域波形、频谱,并将(3)和(4)进行比较。
2.DSB调制解调原理。抑制载波的双边带调制(DSB-SC),简称DSB,也称线性调制是用原始信号去控制高频载波的振幅,使其随调制信号的规律变化的过程。它是在AM信号中将载波抑制,去掉直流分量,从而输出抑制载波的双边带信号[1]。其时域表达式为:s(t)=m(t)*cos(2πfct),m(t)是原始信号,f■是载波信号的频率,与cos(2πfct)相乘得到已调信号。在频域上,通过调制相当于把基带信号的频谱搬移到载波中心频率的附近,已调信号的频谱可表示为SDSB(ω)=(1/2)·[M(ω+ω■)+M(ω-ω■)]。该已调信号经过信道的传输,叠加噪声,到达接收端经过相干解调恢复出基带信号,相干解调由乘法器和低通滤波器组成。在设计中,假设生成的本地载波与接收信号的载波同频同相,低通滤波器滤的设计是课程设计的难点。
3.数字低通滤波器的设计。利用MATLAB进行低通滤波器的设计,其关键是确定基带信号的通带和阻带截止频率。在MATLAB中设计滤波器的方式有多种[3][4],本文选择巴特沃兹低通滤波器。主要用到以下几个MATLAB内部的函数:
[N,wc]=buttord(wp,ws,Rp,As):其中wp,ws分别为通带和阻带的截止频率,取值范围为0~1,在调用时对二分之一采样频率进行归一化;Rp为通带的纹波系数,表示通带范围内信号的波动幅度,As为阻带的衰减系数,表示阻带的衰减幅度;N为低通滤波器的阶数,wc为低通滤波器的3dB截止频率。
[B,A]=butter(N,wc):该函数的作用是计算滤波器系统函数分子分母多项式B和A。得到A和B的值后可以用freqz函数画出低通滤波器的频率响应曲线,利用Y=filter(B,A,y)可以得到通过滤波器之后的信号Y,其中y是滤波前的信号。
三、仿真结果及部分代码分析
按照课程设计要求,生成消息信号,其MATLAB仿真代码如下:
T=0.2;Ts=0.001;N=T/Ts;t=[-N/2:N/2-1]*Ts;x=sinc(100/pi*t);
调制过程:fc=250;y=x.*cos(2*pi*fc*t);
基带信号频谱:fs=1/Ts;df=fs/N;f=[-N/2:N/2-1]*df;X=fftshift(fft(x))/N;
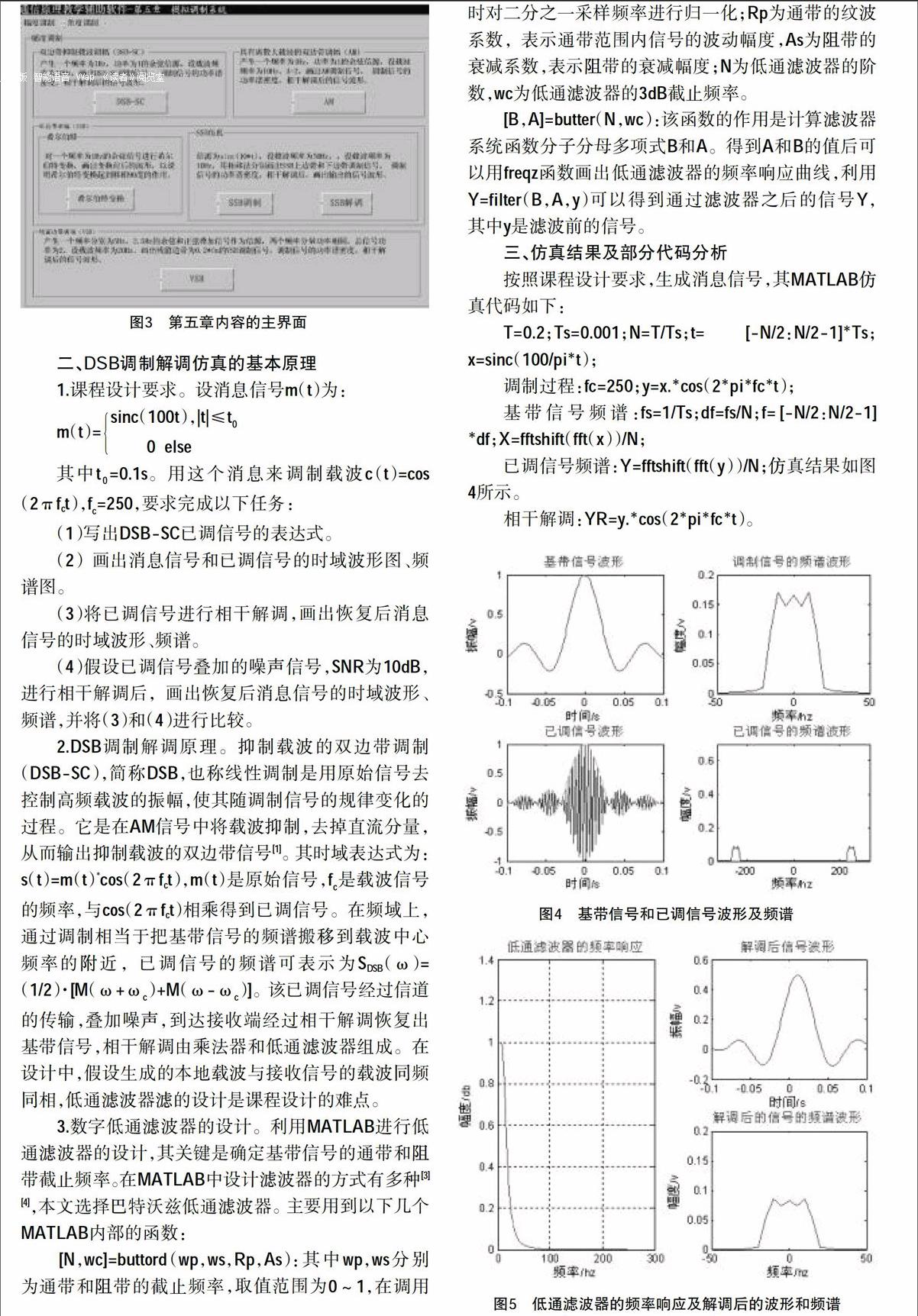
已调信号频谱:Y=fftshift(fft(y))/N;仿真结果如图4所示。
相干解调:YR=y.*cos(2*pi*fc*t)。
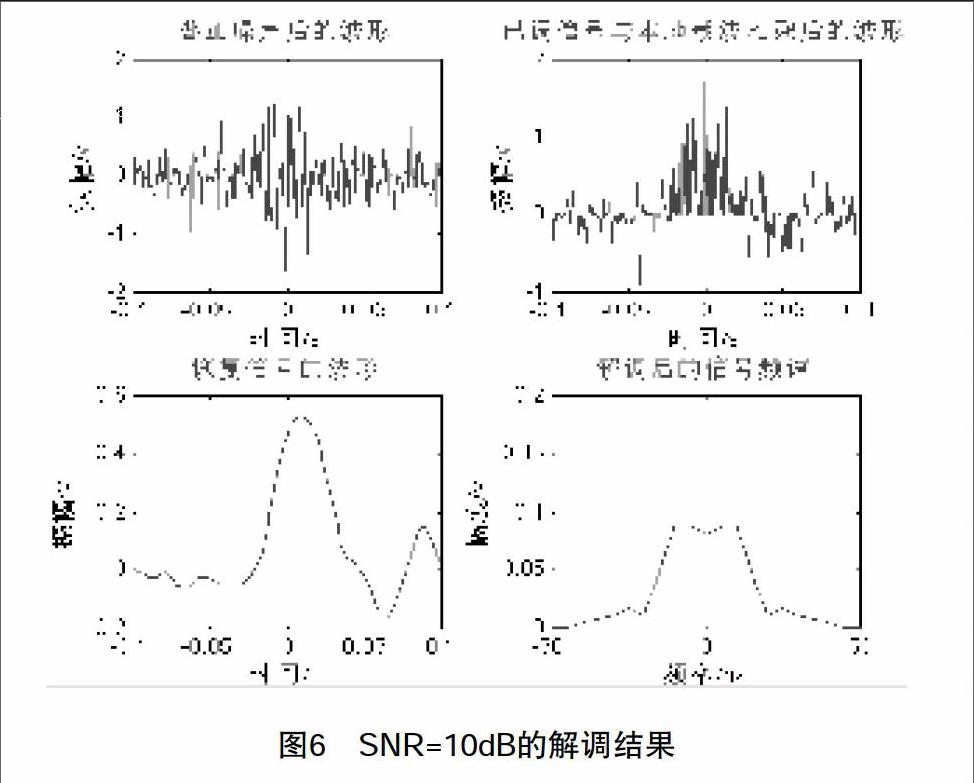
巴特沃斯滤波器设计:从图4可见,基带信号带宽约为23Hz,因此设计低通滤波器时,通带边缘频率取为30Hz,又知采样频率为1000Hz,则得到wp=30/500;阻带边缘频率取为50Hz,则ws=50/500;Rp=1;As=25;[N_,wc]=buttord(wp,ws,Rp,As);[B,A]=butter(N_,wc);HY=filter(B,A,YR);[H_Y,w]=freqz(B,A,512)。仿真结果如图5所示,设计的低通滤波器有较好频率响应,实现了DSB的相干解调过程。图6是通过信道传输叠加了噪声之后的解调过程,可见当信噪比为10dB时,恢复的信号已经出现失真。
四、结束语
在通信原理教学过程中,利用MATLAB仿真软件将抽象的知识点以图形图像方式展示,不仅有利于教师授课,更有利于帮助学生自我学习和动手实践,能够有效避免理论教学与实践教学产生脱节,能帮助学生更好地理解和掌握理论知识,激起学生的学习兴趣。本文基于“通信原理教学辅助软件平台”,主要利用了软件中“DSB模拟调制和解调”模块的开放代码,在MATLAB环境下模拟了双边带幅度调制和解调的基本过程,并重点设计了低通滤波器,达到了课程设计的要求,双边带幅度调制与解调(DSB)理解更加深刻。通过实践表明,该“通信原理教学辅助软件平台”为通信原理的理论学习提供了一个良好的平台。
参考文献:
[1]樊昌信,曹丽娜,等.通信原理[M].第六版.北京:国防工业出版社,2010.
[2]彭红平,杨福宝.基于Matlab的FIR数字滤波器设计[J].武汉理工大学学报:信息与管理工程版,2005,27(5):275-278.
[3]何丽娜,叶听,汪伟.数字滤波器(FIR)设计算法研究[J].电声技术,2014,38(2):67-70.
[4]朱静,徐军.用MATLAB对双边带抑制载波调制解调器的仿真分析[J].湖南城建高等专科学校学报,2002,11(4):20-23.
[5]王智忠,幅度调制信号的特性分析及其MATLAB仿真研究[J].安徽理工大学学报:自然科学版,2006,26(3):48-51
[6]李红.基于Matlab的线性模拟调制技术研究[J].科技广场,2010,(7):32-34.endprint