一种基于NSCT和自适应PCNN医学图像融合的改进算法

陈俊强，黄丹飞

（长春理工大学 生命科学技术学院，长春 130022）

随着医学图像技术快速发展，图像的清晰度已经得到了很大提高，由于医学图像是由不同设备共同获取的，使用单独的一类医学图像，通常不能给医生提供完整的病理信息，所以经常要融合不同类型的医学图像来获取想要的病理信息，从而为进一步综合地理解病理信息做出精准地判断［1］。

目前小波变换已经广泛应用到多模态医学图像的融合处理中［2］，但其只能分解成三个各向同性的方向，不能够分解成任意的方向来提取图像的细节信息，小波变换会产生方块效应，这会影响融合图像的效果［7］。为了解决小波变换的缺点，Do M N和Vetterli M提出了Contourlet变换，该变换除了有小波变换的尺度和频域特性，还具有多尺度方向特性，可以更全面地表达图像的细节信息［3］。但是，Contourlet变换要对图像进行降采样，这会使得Contourlet变换不具有平移不变性而产生伪轮廓现象。为了解决Contourlet变换不具有平移不变性的问题，Cunha A L等提出了一种具有平移不变性的Contourlet变换，即NSCT，该变换不会产生伪轮廓现象［4］。虽然非降采样Contourlet变换已经开始应用于多模态医学图像的处理中，但是只有好的融合规则才会有好的融合效果。区域能量规则已经广泛应用到图像融合中［5］，但是该规则是针对一个区域进行操作的过程，并不能完全地利用每个像素之间的关系，这会丢失原始图像中的细节信息，而PCNN就很好地解决了这个问题［6］，但是当前PCNN算法还有很多的局限性，并不能很好地利用PCNN的自动处理能力。

针对以上存在的问题，本文提出了一种基于NSCT自适应PCNN的医学图像的融合算法。首先对原始图像进行分解操作，分解后获得低频系数和各带通方向系数；然后对低频系数采用边缘信息最大准则来选择融合的低频系数，各带通系数采用基于视觉神经元模型的自适应PCNN模型来选择融合各带通系数；最后经NSCT的重构来得到融合后的图像。

1 NSCT自适应PCNN图像融合

1.1 NSCT算法原理

NSCT先经过非降采样金字塔滤波器组（Nonsubsampled Pyramid Filter Bank，NSPFB）来实施多个尺度的分解，再经过非降采样方向滤波器组（Nosubsampled Directional Filter Bank，NSDFB）来对各带通图像实施多个方向的分解，获得变换后的多尺度、多方向带通的系数［8］。NSCT分解的频域示意图如图1所示。

非降采样金字塔滤波器组（NSPFB）是两路二维的分降采样的滤波器组。该滤波器组是在拉普拉斯金字塔变换过程中除去了降采样过程来实现非采样金字塔变换的分解与重构过程的［9］。非采样金字塔变换的分解与重构示意图如图2所示。

图2 双通道非采样金字塔滤波器组

非降采样方向滤波器组（NSDFB）是两路二维的非采样滤波器组。通过具有扇形结构的非采样迭代方向滤波器组来实现两路非采样的方向分解与重构［10］。非采样方向滤波器组的结构示意图如图3所示。

图3 双通道非采样方向滤波器组

1.2 PCNN原理

PCNN模型是由很多神经元相互连接而形成的单层循环网络，其中单个神经元是由接收区域、耦合调制域和脉冲发生域组成［11］，单个神经元模型如图4所示。

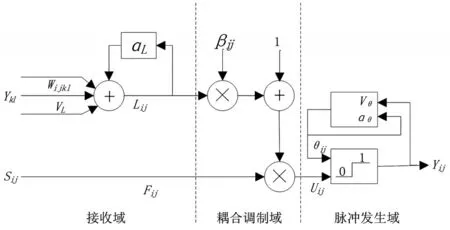
图4 PCNN神经元结构

接收域由循环输入Fij线路和线性连通输入Lij线路构成，其中循环输入Fij直接获取来自外部的刺激信号输入Sij，线性连通输入Lij获取来自一定区域内相连接的神经元信号Ykl。耦合调制域是将带有偏置的线性连通输入单元与循环输入单元进行相乘来得到神经元的内部参数Uij。脉冲发生域的构成有脉冲发生器和临界值变化的匹配器，在神经元的内部参数Uij大于该神经元膜电位的动态临界值θij时，神经元会输出一个Yij信息。

当PCNN模型用于处理二维图像时，可以用数学离散形式来描述，如公式（1）所示。

其中，Sij为外部信号，αL和αθ分别是线性连通输入Lij和动态临界值θij的衰减定值，VL和Vθ分别是连通倍数系数和临界值倍数系数，Wijkl是线性连通输入Lij的加权系数，βij为连接强度，决定了线性连通输入Lij对内部参数Uij的贡献。

1.3 基于NSCT和PCNN的图像融合及其改进

目前，NSCT主要采用NSPFB进行多个尺度的分解，由于拉普拉斯金字塔变换后会产生冗余信息，而小波变换不会产生冗余信息，并且在各个尺度上还能分解出三个不同方向的细节信息，所以提出采用非降采样小波滤波器组来替代NSPFB组。

当前PCNN的连接强度β参数经常被设为定值，极大地限制了PCNN的自动选择和使用的通用性，所以提出用图像的区域能量和图像的可见度来计算PCNN的连接强度β值，因此PCNN能够依据图像本身所具有的特征来自动设置连接强度β值。

本文提出的基于NSCT自适应PCNN的图像融合框图如图5所示。具体的融合步骤如下：

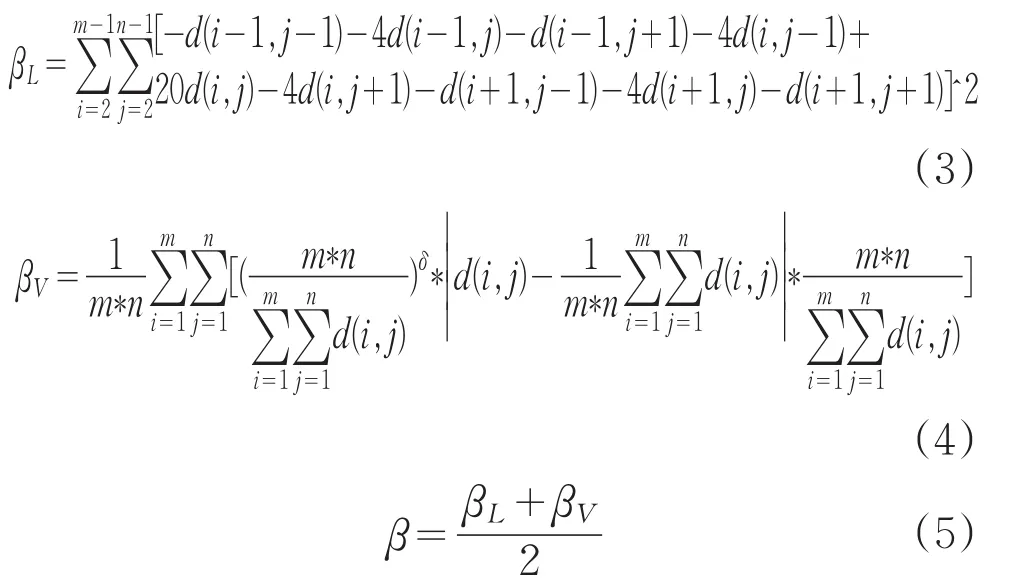
（4）当计算总数为200时，计算停止。依据图像A和B的各个高频系数的叠加次数TAj,k和TBj,k的数值来选取融合后各带通方向的系数，即：

（5）将获得的融合低频系数和融合各带通方向系数经NSCT的重构得到最后的融合图像。

2 实验结果与分析

为了证明本文提出算法的正确性和实用性，本文采用来自同一部位的MRI和PET病理图像进行仿真实验。为了更好的进行比较，采用了三种融合算法进行比较，如图6所示。其中图6（a）为MRI图像，图6（b）为PET图像，对这两幅图像分别采用基于小波区域能量最大融合算法（融合结果如图6（c）所示）、基于离散Curvelet区域能量最大融合算法（融合结果如图6（d）所示）、NSCT-PCNN算法（融合结果如图6（e）所示），图6（f）、6（g）、6（h）分别为6（c）、6（d）、6（e）的局部放大图。图像融合效果指标对比见表1。

图5 NSCT_PCNN图像融合框图

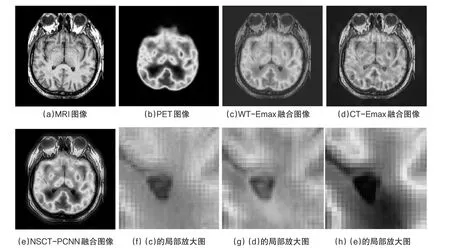
图6 MRI和PET图像及各种方法融合结果

表1 融合效果指标对比

从图6可以看出，NSCT-PCNN融合算法的融合图像整体亮度高、边缘和空间纹理清晰、颜色失真小，整体效果明显优于其他两种算法的效果。从三种融合方法的局部放大图可以看出，基于小波算法和Curvelet算法的融合图像在边界处存在明显的伪轮廓现象，而NSCT-PCNN算法的融合图像在边界处轮廓很分明，没有伪轮廓现象。从表1可以看出，NSCT-PCNN融合算法的平均梯度、边缘强度、信息熵、互信息指标明显优于其他两种算法，表明NSCT-PCNN融合算法不但大大提升了融合图像的纹理细节信息，此外还保留了原始数据的特征。

3 结论

NSCT函数有尺度参数、平移参数和方向参数，这使得非采样Contourlet变换具有良好的空间特性、频率特性和全方位特性，能够更好地表征图像细节特征信息，此外还具有平移不变特性，很好地解决了伪轮廓问题，更好地体现非采样Contourlet变换在各尺度各方向上分解优势，从而有利于融合计算的实现。据此，本文采用非降采样Contourlet变换应用于医学图像中，并采用了具有视觉神经元模型特点的自适应PCNN模型，提出了一种基于非降采样Contourlet变换自适应PCNN的融合算法。本文算法用于MRI和PET医学图像融合，同时和小波算法和Curvelet算法进行比较，实验仿真结果表明本文算法有效并正确地融合了MRI和PET医学图像信息。本文使用产生冗余信息更少、更易快速实现的9-7小波滤波器组替代了拉普拉斯金字塔滤波器组，其次是传统PCNN的连接强度β是定值，限制了PCNN的自动处理能力和使用的普遍性，因此分别采用图像拉普拉斯区域能量和图像可见度函数来自适应地设置连接强度β，这使得融合图像边缘和空间纹理信息清晰、颜色失真小，没有伪轮廓现象，很好地保留原有图像的特征信息。

［1］叶传奇.基于多尺度分解的多传感器图像融合算法研究［D］.西安：西安电子科技大学，2009.

［2］杨波.基于小波的像素级图像融合算法研究［D］.上海：上海交通大学，2008.

［3］Do M N，Vetterli M.The contourlet transform：an efficient directional multiresolution image representation［J］.IEEE Transaction on Image Processing，2005，14（12）：2091-2106.

［4］Cunha A L da，Zhou J P，Do M N.The nonsubsampled contourlet transform：theory，design，and applications［J］.IEEE Transaction on Image Processing，2006，15（10）：3089-3101.

［5］邹容，李玲玲，李翠华.基于非下采样Contourlet的多聚焦图像融合方法［J］.厦门大学报，2009，48（6）：812-816.

［6］Deng H B，Ma Y D.Image fusion based on steerable pyramid and PCNN［A］.International Conference on Applications ofDigitalInformation and Web Technologies，IEEE，2009：569-573.

［7］王昕，李玮琳，刘富.小波域CT/MRI医学图像融合新方法［J］.吉林大学学报：工学版，2013，43（S1）：25-28.

［8］徐苏.基于Contourlet的医学图像融合技术探讨［J］.中国医学影像技术，2011，27（11）：2326-2330.

［9］张莹，李言俊，张科.基于NSCT的红外与可见光图像融合［J］.计算机工程与应用，2011，47（3）：196-198.

［10］王玲，李红松，周浩.基于非向下采样Contourlet变换的多聚焦图像融合［J］.计算机应用与软件，2011，28（4）：167-170.

［11］温黎茗，彭力，徐红.基于NSCT和PCNN的遥感图像融合算法［J］.计算机工程，2012，35（11）：19-195.