一种高效的全局K-均值算法

梁鲜，曲福恒，杨勇，才华

（1.长春理工大学 计算机科学技术学院，长春 130022；2.长春理工大学 电子信息工程学院，长春 130022）

聚类［1］分析是一种无先验知识的机器学习过程，是数据挖掘一个重要的分支，遵循同一个集合中的样本相似性最大，不同集合中的样本相异性最大的理念［2］，把样本集分为若干个集合，每个集合称为一个聚簇。已有的经典聚类算法大致可分为五种：基于层次的、基于划分的、基于密度的、基于网格的和基于模型的。K-均值是一种基于划分的聚类算法，因效率高，处理速度快等特点，适合对大数据集聚类。K-均值算法选择初始聚类中心的随机性，使聚类结果因不同初始聚类中心和不同初始数据输入顺序的影响而波动，聚类结果仅能收敛到局部最优。

针对K-均值算法的不足，很多学者提出一系列改进算法。Grigorios Tzortzis选取相距最远的样本作为前两个初始聚类中心，按照最小最大原则选取下一个聚类中心，保证每次选择的聚类中心距已有聚类中心较远，得到正确的初始聚类中心；Kong Dexi把核函数引入到K-均值算法中，把数据映射到高维空间（或核空间），在高维空间中使用K-均值对数据聚类，使用正定核（CPD）提高算法效率；Hassanzadeh提出萤火虫算法和K-均值结合的算法，对数据集细化，找到子数据集的质心，提高算法的精度和性能；但是这些算法没有得到广泛的认可，Likas A等人在2003年提出全局K-均值算法［6］增量选择初始聚类中心，得到全局最优的聚类结果，但算法时间复杂度大，不适合对大数据集聚类。本文提出全局K-均值的改进算法，在不影响聚类效果的基础上，减少聚类时间。

1 K-均值

K-均值算法相关描述［7］：设样本集X={xi|i=1,2,...,N}，K个类别为Cj（j=1,2,...,K），K个聚类中心为Aj（j=1,2,...,K）。

样本间的欧式距离公式：

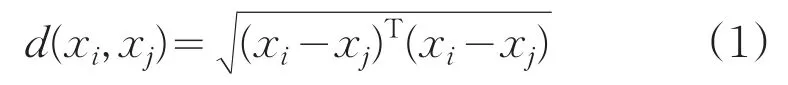
聚簇中心：

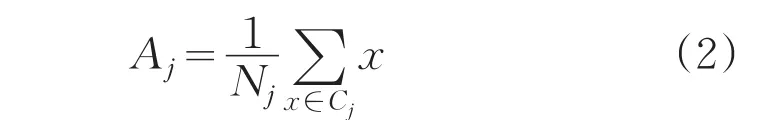
误差平方准则函数：

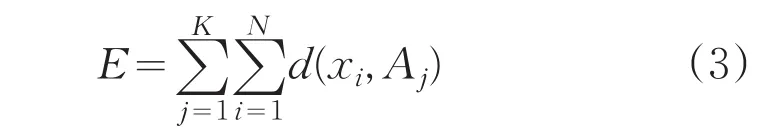
K-均值算法流程图如图1所示。

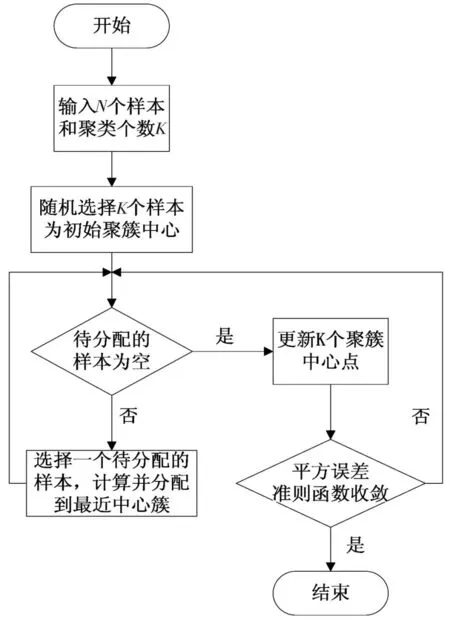
图1 K-均值算法流程图

2 全局K-均值

全局K-均值算法通过求解一系列子聚类问题来解决K个聚簇的问题。该算法使用K-均值算法局域搜索的能力得到全局优化的聚类结果。为了克服初始值敏感的问题，该算法通过每一次传统K-均值算法找出一个最佳聚簇中心，直到找出K个聚簇中心。该算法具体步骤是：首先从实现一个聚簇的聚类问题开始，设置K=1，即先找到第一个聚簇的最佳质心。在这个基础上，实现两个聚簇的聚类问题，设置K=2，找到的K=1的聚簇质心默认为K=2时的一个最佳聚簇中心，迭代地让剩余样本假设为第二个聚簇中心，然后运行K-均值算法，找到误差平方准则函数最小时对应的样本作为另一个最佳聚簇中心，重复该过程，直到找到K个最佳聚簇中心。算法描述如下：

（1）初始化：计算所有样本的均值当做第一个最佳聚簇中心，设置 t=1；

（2）结束条件：t=t+1，当t＞K时，算法终止；

（3）查找下一个最佳聚簇中心：前t-1个最佳聚簇中心为m1，m2，...，mt-1迭代地让剩余样本作为最佳聚簇中心，运行K-均值算法，找到误差平方准则函数最小时对应的样本作为第t个最佳聚簇中心，即K=t的最佳聚簇中心为b1,b2,...,bt；

（4）让 mj=bj,j=1,2,...,t，转到（2）。

3 快速全局K-均值

全局K-均值算法可以得到较好的聚类结果，但是计算量太大。Likas等人对全局K-均值算法进行改进，得到快速全局K-均值算法，该算法通过计算bn，选择bn最大时对应的样本作为最佳聚簇中心，进而减少计算量。

bn的定义如：

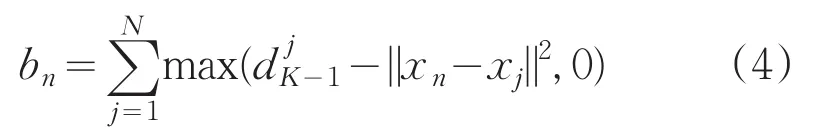
4 一种高效的全局K-均值算法

针对全局K-均值算法时间复杂度大的问题，提出改进算法，继承全局K-均值算法增量选择初始聚簇中心的思想，定义目标函数：

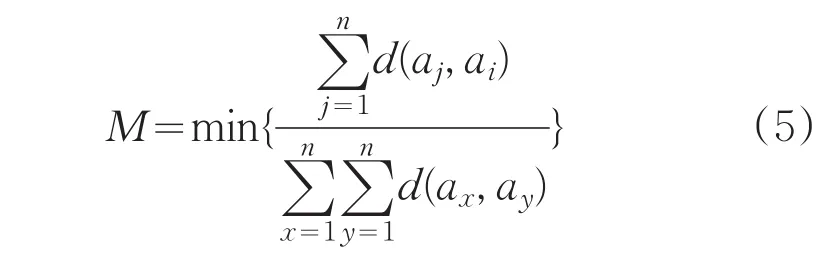
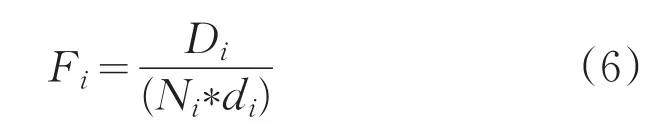
选择正确的初始聚类中心，减少迭代次数，降低时间复杂度。定义目标函数：

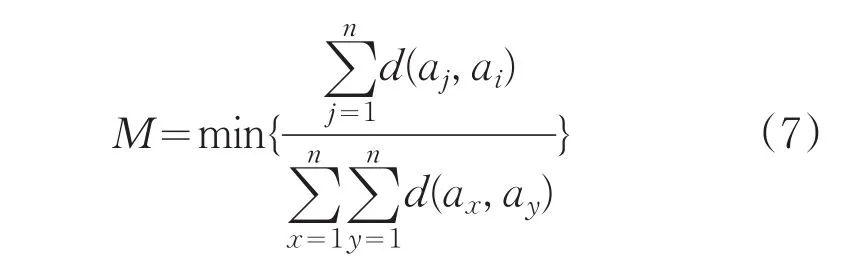
选择数据集中周围分布最密集的样本作为第一个初始聚类中心，选择使目标函数：

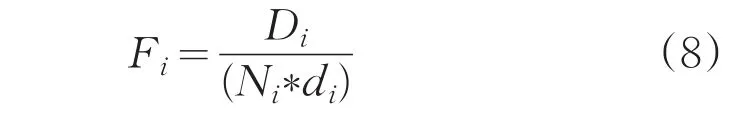
取最小值的样本（距离已有聚类中心远，形成的子簇包含样本个数多并且凝聚度小），作为下一个聚类中心，直到选出K个最佳聚类中心。实验证明算法在不影响聚类性能的基础上减小聚类时间。

问题描述：把样本集合A=（a1,a2,...,an）划分K个聚簇，使误差平方准则函数E最小，该算法使用欧式距离度量两个样本的相似度。

算法描述：

（1）计算

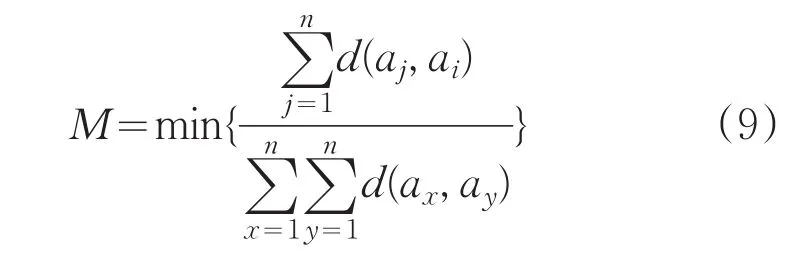
其中，i=1，2，...，n。

最终M的取值对应的样本作为第一个最佳聚簇中心，设置w=1；

（2）另w=w+1，如果簇的个数w＞K，该算法结束，转到Step4；

（3）选取下一个聚簇中心，对剩余样本，计算

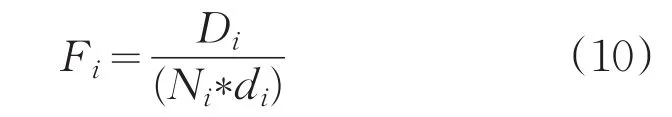
其中，Di是样本ai为聚簇中心形成的子簇中样本到簇心的距离之和，Ni是子簇中样本个数，di是ai到已有最佳聚簇中心的距离和，Fi最小时对应的样本ai作为下一个最佳聚簇中心，转到Step2；

（4）用得到的K个聚簇中心作为K-均值算法的初始聚簇中心，按照就近原则分配样本到距离最近的簇中，分配完毕，更新聚簇中心，直到目标函数收敛。

5 实验结果分析

实验目的是证明改进算法的性能。硬件运行环境是Intel CPU，2.99G内存，931G硬盘；软件运行环境是WindowsXP操作统，Visual Studio 2013开发平台，算法使用C++作为编程语言。

选用Segmentation数据集、pixel averages数据集和Pendigits数据集作为测试数据集，在测试数据集上分别运行10次改进算法、全局K-均值算法、快速全局K-均值算法、K-Means++和Pifs K-均值算法，对测试数据集聚类个数分别为3、4、5、6、7、8、9、10比较平均聚类结果。测试数据集描述如表1所示，算法在Segmentation数据集上平均聚类误差比较如图2所示，平均聚类时间比较如图3所示，算法在pixel averages数据集上平均聚类误差比较如图4所示，平均聚类时间比较如图5所示，算法在Pendigits数据集上平均聚类误差比较如图6所示，平均聚类时间比较如图7所示。

表1 测试数据集的描述

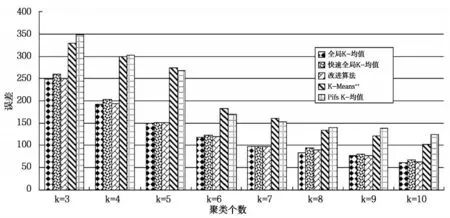
图2 Segmentation测试数据集上聚类误差比较

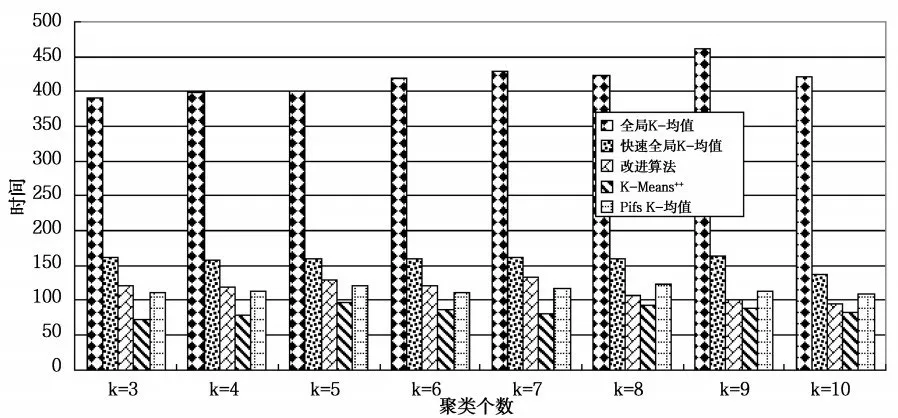
图3 Segmentation测试数据集上聚类时间比较

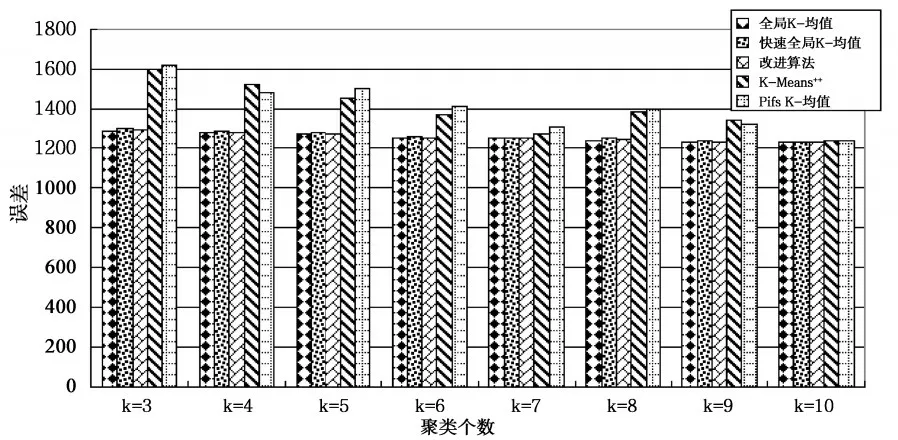
图4 pixel averages测试数据集上聚类误差比较

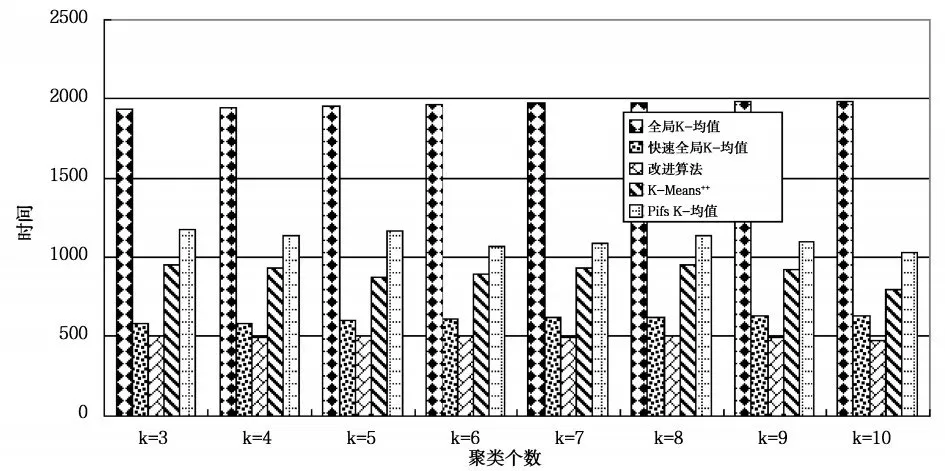
图5 在pixel averages测试数据集上聚类时间比较

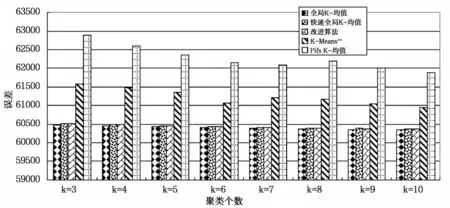
图6 Pendigits测试数据集上聚类误差比较

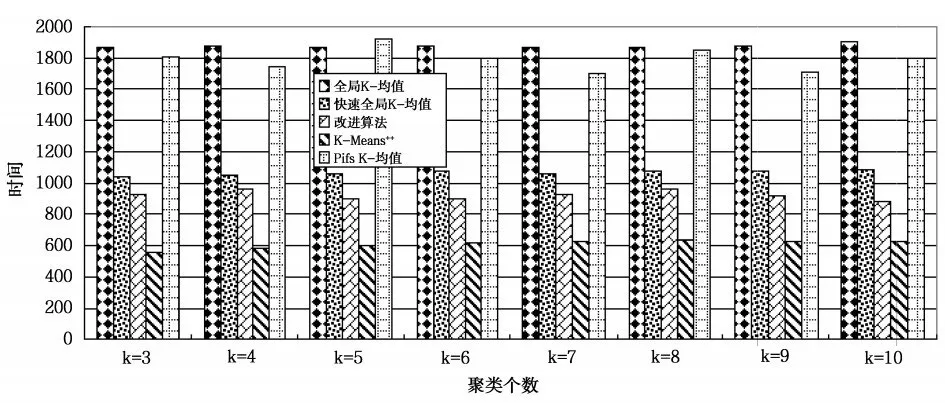
图7 在Pendigits测试数据集上聚类时间比较

由图2、图4和图6可知，改进算法与全局K-均值算法、快速全局K-均值算法相比，不影响聚类误差，与K-Means++和Pifs K-均值相比，聚类误差小，聚类效果更好。由图3、5和7可知，改进算法相比全局K-均值算法、快速全局K-均值算法减小了聚类时间，聚类个数为正确值时，聚类时间减小量最大，在Segmentation和Pendigits数据集上，改进算法的聚类时间大于K-Means++算法，相比Pifs K-均值算法时间复杂度小。实验证明，改进算法可以得到更好的聚类结果，与全局K-均值算法、快速全局K-均值算法相比，降低了时间复杂度，与优化初始聚类中心的其它K-均值算法相比，得到更好的聚类效果，聚类时间上也有一定的优势，证明改进算法是可行的。

6 结束语

为了解决全局K-均值算法时间复杂度大的问题，定义新的目标函数，选择最小化目标函数贡献大，并且和已有聚类中心距离远的样本作为下一个聚类中心，选择周围分布较密集的样本作为第一个初始聚类中心，得到一种高效的全局K-均值算法。实验证明，改进算法相比全局K-均值算法、快速全局K-均值算法，在不影响聚类效果的基础上，降低了时间复杂度，与优化初始聚类中心的其它K-均值算法的比较结果表明，改进算法选取正确的初始聚类中心，得到更好的聚类效果，聚类时间上也有一定的优势。

［1］Yukio Ohsawa，Katsutoshi Yada.Data mining for design and marketing［M］.CRC Rress，2009.

［2］Aswani K C，Srinivas S.Concept lattice reduction using fuzzy K-means clustering［J］.Expert System with Application，2010，37（3）：2696-2704.

［3］Grigorios Tzortzis，Aristidis Likas.The min max K-means clustering algorithm［J］.Pattern Recognition，2014：47（2）：2505-2516.

［4］Kong Dexi，Kong Rui.A fast and effective kernel based K-Means clustering Algorithm［C］.IEEE Intelligent Systems，2013：58-61.

［5］Hassanzadeh T，Meybodi，M R.A new hybrid approach fordata clustering using firefly algorithm and K-means［C］.IEEE Intelligent Systems，2012：7-11.

［6］Likas A，Vlassis M，Verbeek J.The global K-means clustering algorothm［J］.Pattern Recognition，2003，36（2）：451-461.

［7］Erisoglu M，Calis N，Sakallioglu S.A new algorithm for initial cluster centers in K-means algorithm.Pattern Recognition Letters，2011（32）：1701-1705.