归类小结法在积分上限函数学习中的应用

杨海霞

(兰州文理学院师范学院，兰州 730000)

学习高等数学要有一种精神，用大数学家华罗庚的话来说，就是要有“学、思、锲而不舍”的精神。高等数学中的一些内容如积分上限函数、函数的连续与间断、积分的换元法等一时很难理解，需要每个同学反复琢磨、反复思考、反复训练，通过典型例题比较，才能真正掌握。本文以积分学中一类特殊的、有着广泛应用的但又难掌握的积分上限函数为例，说明如何应用这一方法，将所学内容经过思考加工、归纳总结，使学生轻松地巩固所学知识，提高学习高等数学的兴趣。

在积分学中，为证明原函数的存在定理和牛顿－莱布尼兹公式，引进积分上限函数(或变上限定积分)的概念［1－2］。积分上限函数 F(x)=的自变量是上限变量x，在求导时是关于x求导，但在求积分时，则把x看作常数，积分变量t在积分区间［a，x］上变动。

1 积分上限函数

1.1 积分上限函数的性质

定理1［2］如果 f(x)在［a，b］上可积，则上连续。

定理2［2］如果 f(x)在［a，b］上连续，则上可导，且 F'(x)=

1.2 特殊的积分上限函数

以上介绍了积分上限函数的相关知识，下面以积分上限函数中的代表性问题为例［3-6］，详细说明如何灵活应用归类法解决与此类函数有关的实际问题。

2 积分上限函数的应用

2.1 极限问题

这类问题的求解经常会用到洛必达法则。

2.2 求导问题

1)计算导数

2)讨论单调性

例6设f(x)在(-∞，+∞)内连续且f(x)＞0，讨论 φ(x)在(0，+∞)的单调性。思路:利用F'(x)的符号可以判定。答案:单调增加。

2.3 最值极值问题

利用可导函数的一阶导数和二阶导数来判定函数的极值点问题，进而讨论最值问题。

例7 如图1所示，在区间［1，e］上求一点ξ，使得图中所示的阴影部分的面积为最小。思路:阴影部分的面积可以表达为两个变限定积分之和:-lnt)dt，然后通过导数S(x)求出其驻点。答案

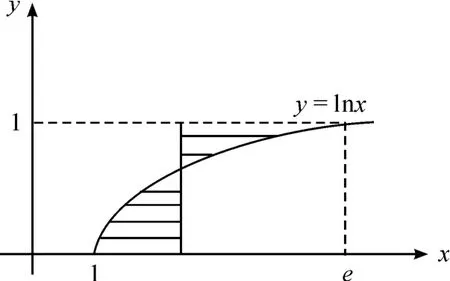
图1 例7

2.4 积分问题

1)求积分

反向支付和解协议虽然能使原研药企业和首仿药申请人实现利益的最大化，但却损害了消费者利益。首仿药上市时间的推迟将对仿制药市场竞争造成损害，也给药物可及性带来不利影响。为对反向支付和解行为进行规制，美国不仅对专利链接制度本身进行了修改，而且还通过反垄断审查机制对有关和解协议进行审查。

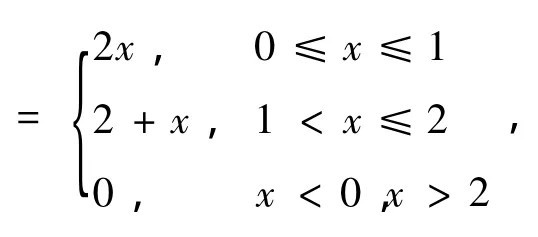
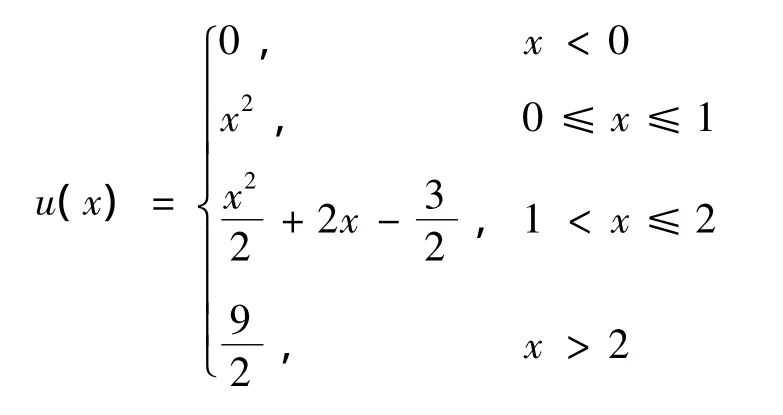
2)含有未知函数的变上限定积分的方程的求解问题

例13设f(x)为正值连续函数，f(0)=1，且对任一 x＞0，曲线 y=f(x)在区间［0，x］上的一段弧长等于此弧段下曲边梯形的面积，求此曲线方程。说明:根据题设列出方程中含有f(x)的积分上限函数。答案

2.5 证明一些积分不等式或等式等

1)证明积分不等式

说明:这类题通常可构造一个辅助函数，利用该函数的单调性来证明。

例14(Cauchy-Swartz不等式) 设f(x)，g(x)均在［a，b］上连续，则思路:利用积分上限函数构造辅助函数，令，则F(a)=0，求出F'(x)并证明F'(x)≥0，从而F(x)单调增加，于是得 F(b)≥F(a)=0，由此可得结论。

例15设f(x)在［0，1］上连续且单调减少，证明:对任一0＜λ＜1，有提示:即证令F(x)=通过证明F'(x)≤0可证F(x)单调减少，即可得结论。

2)证明与中值定理有关的某些积分等式。

例16设f(x)，g(x)在［a，b］上连续，求证:存 在ξ∈(a，b)，使说明:令在［a，b］上用Rolle定理即可证得结论。

例17(积分中值定理) 若函数f(x)在［a，b］上连续，则在［a，b］上至少存在一点 ξ，使得说明:令 f(x)=则用Lagrange中值定理即可证得结论。

2.6 奇偶性与周期性的应用

例18设f(x)是周期为T的连续函数，证明:对于任意的a∈R，有证明:构造辅助函数F(a)dx，所以 F'(a)=f(a+T)-f(a)=0，从而 F(a)=C，又因为 F(0)=，所以，即

高等数学的学习必建立在理解和熟练解题的基础上，死记硬背无济于事。从本文的探讨中可体会到归纳总结为人们思维提供了更广阔的“自由创造”的天地［7－10］，在学习其他知识时也可以触类旁通，从而可提高学习的兴趣。

［1］同济大学应用数学系.高等数学:上册［M］.5版.北京:高等教育出版社，2004.

［2］刘玉琏.数学分析讲义:上册［M］.5版，北京:高等教育出版社，2008.

［3］张辉，景慧丽.积分上限函数相关问题的探讨［J］.高等数学研究，2010，13(6):27－30.

［4］陈熙德.关于积分上限函数及其性质的修改设想［J］.西南民族大学学报，2004，30(1):117－118.

［5］徐虎.积分上限函数的应用研究［J］.内江科技，2008，29(4):86.

［6］景慧丽，屈娜，于宁莉，等.积分上限函数的探究式教学［J］.河南教育学院学报，2013，22(1):54－56.

［7］王少英，王淑云.积分上限函数的性质及其应用［J］.唐山师范学院学报，2008，30(5):20－22.

［8］王宝珍，夏银红.积分上限函数的若干应用［J］.天中学刊，2012，27(2):26－27.

［9］章朝庆.浅议积分上限函数的应用［J］.泰州职业技术学院学报，2010，10(3):60－61.

［10］倪华，田立新.关于积分上限函数的周期性研究［J］.高等数学研究，2011，14(1):9－11.