NGINAR(1)模型参数的拟似然估计

贺天宇，王金山

(陆军军官学院，合肥 230031)

整值时间序列数据在现实生活中是普遍存在的，如医院等待就医的人数、保险公司每月索赔次数、商场中购买某种商品的顾客数等。关于整值时间序列模型的研究成果大多是在经典的“thinning”算子［1］模型的基础上取得的。然而，Ristic［2］提出了一种基于负二项稀疏算子的一阶几何整值自回归过程(NGINAR(1))，为整值时间序列模型注入了新元素。

拟似然(quasi-likelihood)法是一种非参数估计方法，由Wedderburn［3］于1974提出的，是广义最小二乘估计的推广，有着广泛的应用［4－5］。近几年，有部分学者开始尝试利用该方法对整值时间序列模型的参数估计问题进行研究。Zheng［6］研究了p阶随机系数整值自回归过程的拟似然估计;Zheng［7］在提出了一阶随机系数整值自回归过程的同时也研究了其参数的拟似然估计;薄海玲［8］针对INARS(p)模型给出了参数的拟似然估计。但对于NGINAR(1)模型的拟似然估计研究尚属空白。

本文介绍了NGINAR(1)模型的定义以及一些统计性质，利用拟似然估计法给出了模型参数修正的拟似然估计因子的表达式，并证明了其极限分布的正态性;通过数值实验，将MQL估计与Yule－Walker估计和CLS估计进行比较。结果显示，MQL估计在一定程度上较Yule－Walker估计和CLS估计更优。

1 NGINAR(1)模型的定义

定义1［2］由过程

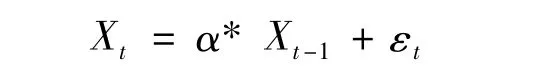
对于NGINAR(1)过程，Ristic［2］得出了一些统计特性，为了行文方便，本文以命题的形式列出部分结论:

2 模型参数的拟似然估计

为了得到模型参数的拟似然估计，首先假设:［H1］{Xt}为NGINAR(1)模型的严平稳遍历解;

设(X1，X2，…，XT)是定义1给出的NGINAR(1)模型的T个样本值，记λ=α(1+α)，则根据命题2有 Vθ(Xt|Xt－1)=Var(Xt|Xt－1)= α(1+ α)Xt－1+= λXt－1+。

下面对参数β=(α，με)'用拟似然法进行估计。记θ=(λ)，由命题1有拟似然估计法的标准估计方程:

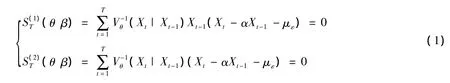
其中:

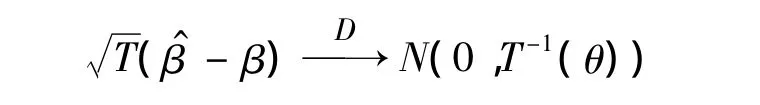
其中:

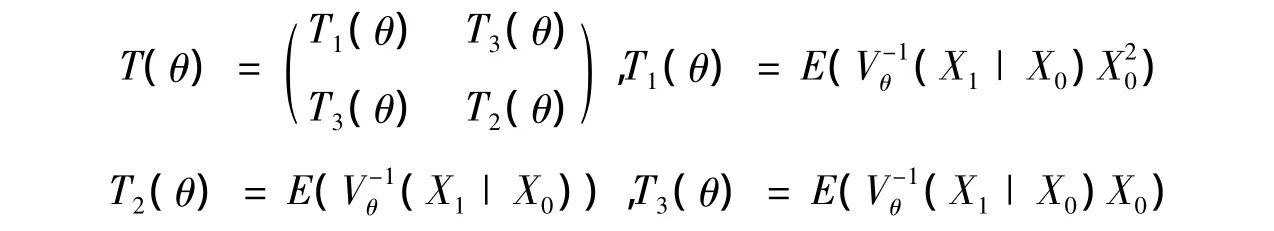
证明 假设 θ已知，令Ft=σ(X0，X1，…，Xt)，则对方程组

有:

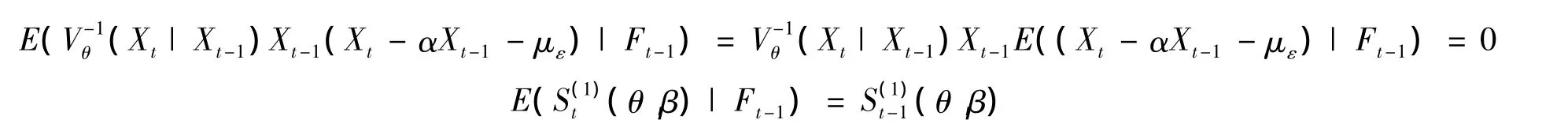
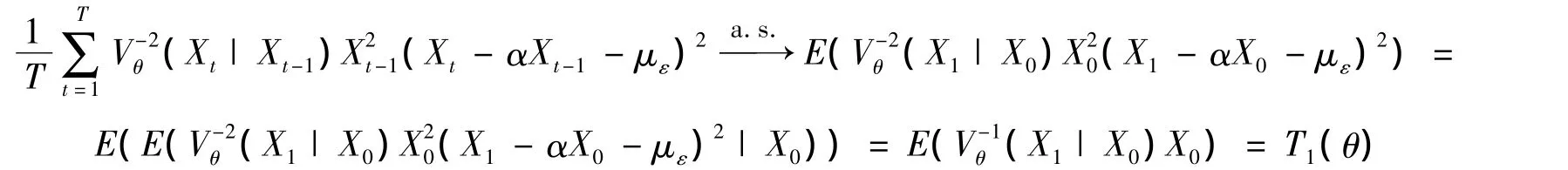
由鞅差中心极限定理［10］知，当T→∞时类似地有

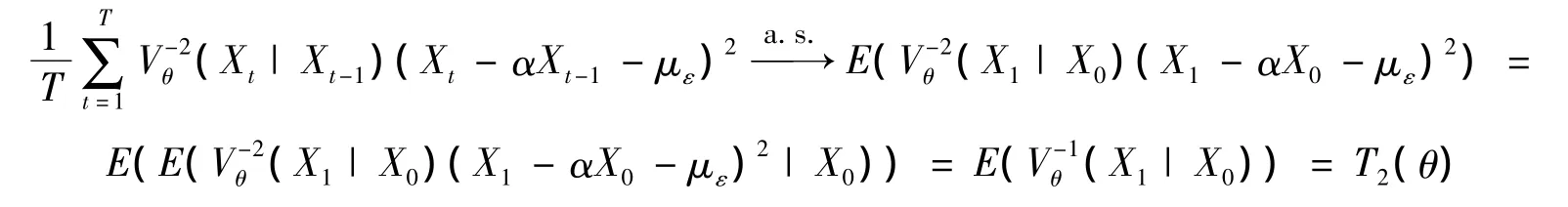
同理，∀k=(k1，k2)∈R2(0，0)，有

由Gramner-Wold方法可得，当T→∞时，

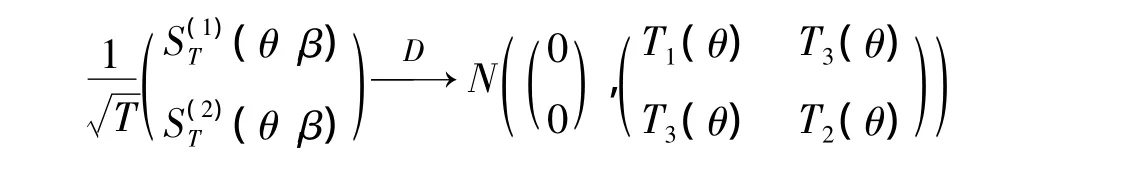
其中 T3(θ)=E((X1|X0))。

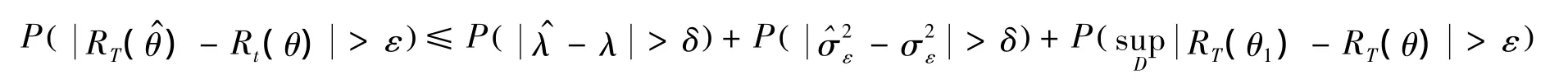
由Markov不等式，有

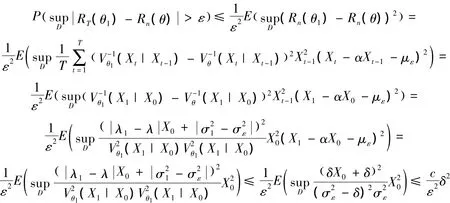
其中0＜c＜∞为常数。

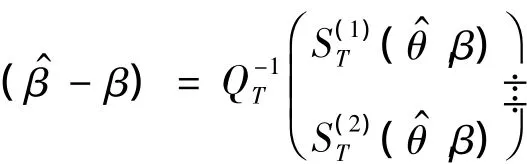
因此，当T→∞时，

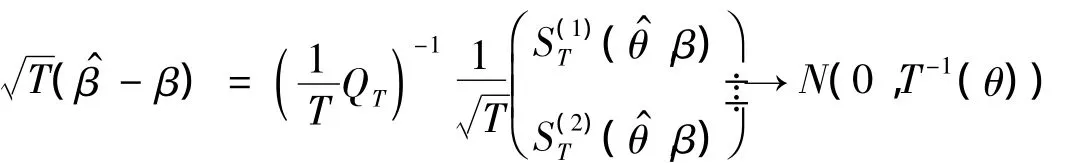
对于θ的相合估计，可以通过条件最小二乘法(CLS)［2］得出。

3 数值实验

首先，计算出τ=(α，με)的CLS估计。令则=arg minτ(Q(τ))。

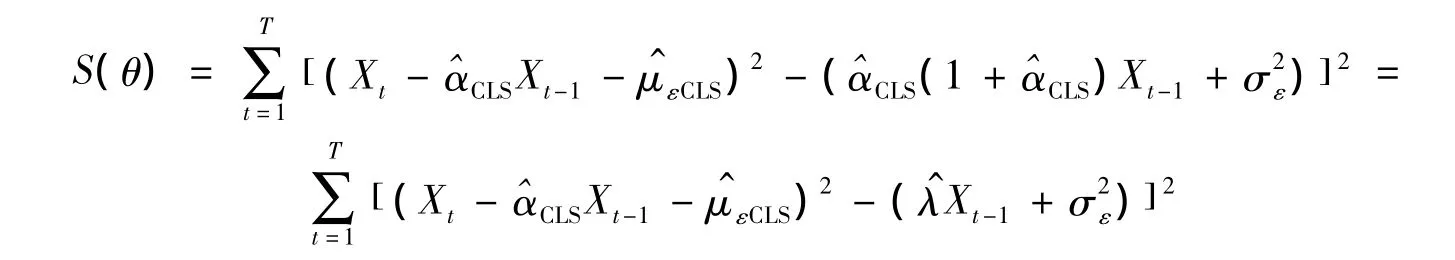
考虑模型 Xt=α*Xt－1+εt，图1给出了当样本个数 T=500，初值 X0=1时的样本路径，其中:(a)α =0.3，με=1;(b)α =0.6，με=0.95。

为了比较不同估计方法的优劣，先借助于Matlab产生相应参数值的样本随机数，再分别对产生的样本值计算参数的CLS估计、Yule-Walker估计和MQL估计，每次模拟均重复500次，并计算出每种估计的经验偏差(Bias)和标准误差(SE)。

表1和表2 分别记录了在选取 α =0.3，με=1 和α =0.6，με=0.95，样本个数 T=100，200，500，800，1000时不同估计的Bias和SE，并以格式(Bias，SE)记录。

由表1和表2可见，不同估计方法的Bias和SE均随着样本个数的增加而减小，在相同条件下MQL估计较CLS估计和Yule-Walker估计更优。

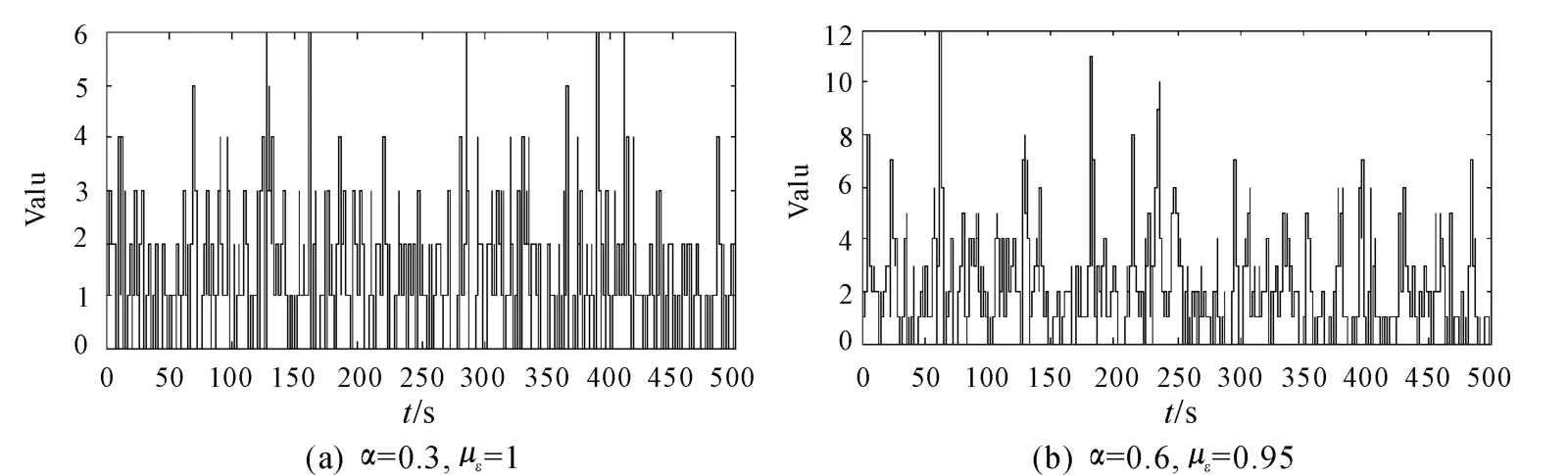
图1 样本路径

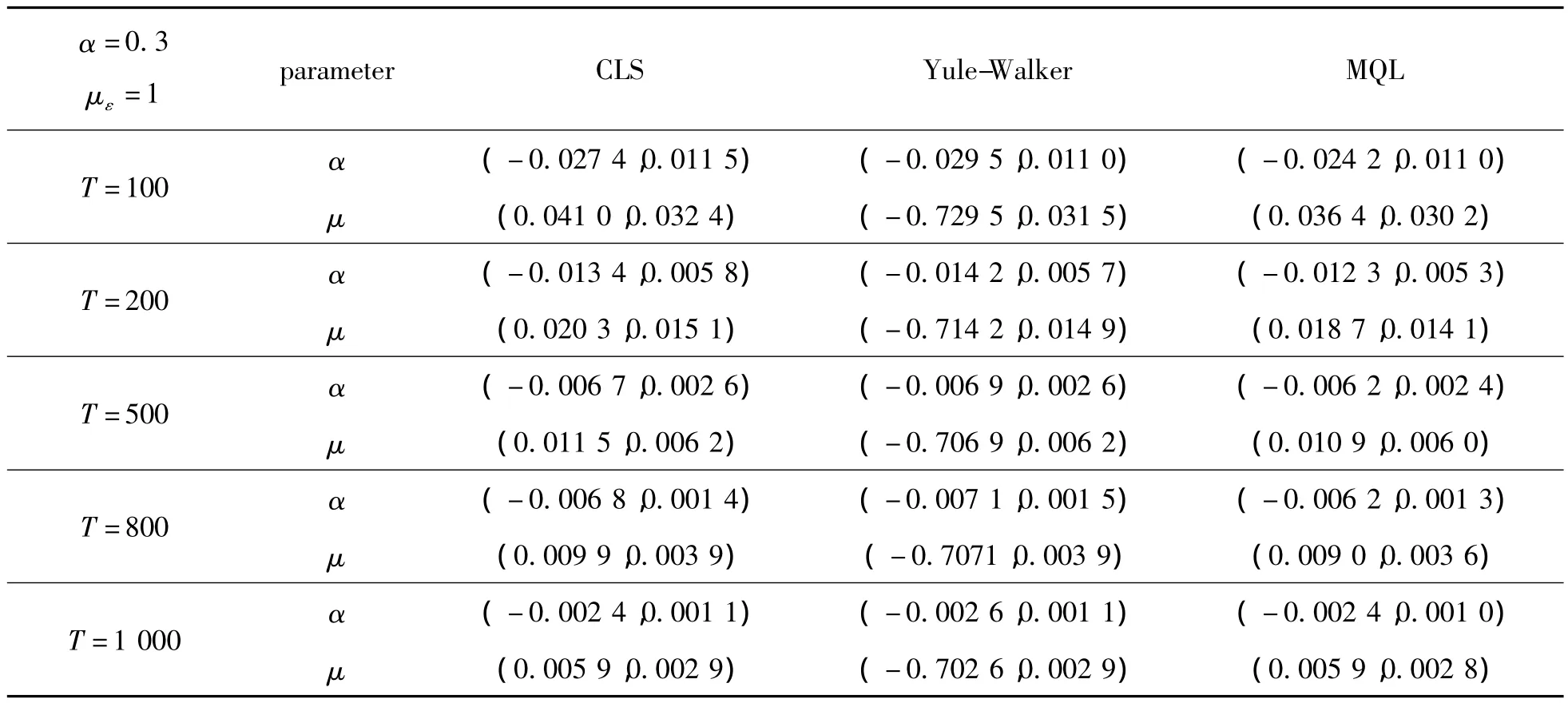
表1 参数估计结果对比I

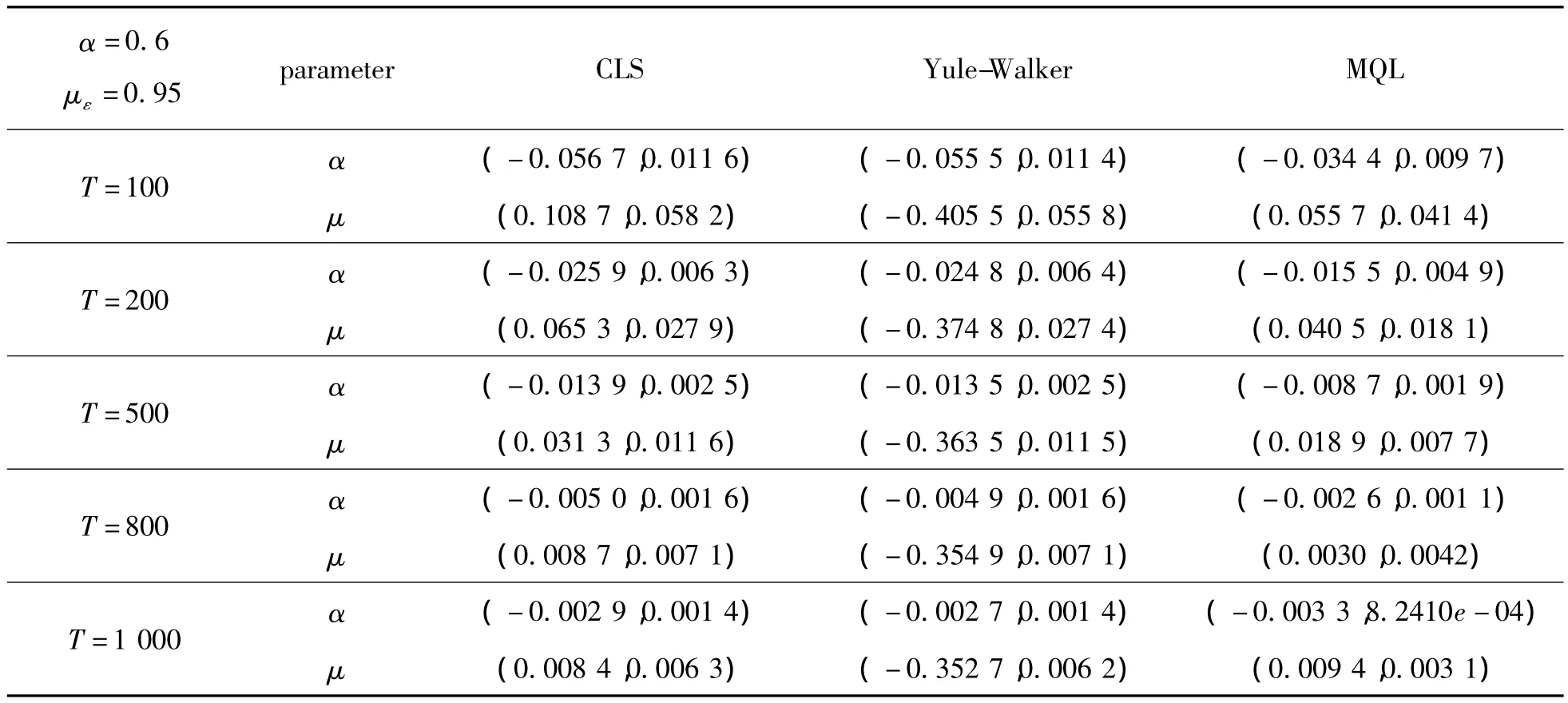
表2 参数估计结果对比II

4 结束语

本文在分析了NGINAR(1)模型统计特性的基础上，利用拟似然方法对模型的参数进行了估计，在给出了参数修正的拟似然估计因子的同时也证明了其极限分布的正态性。通过数值仿真实验证实了参数修正的拟似然估计因子法在参数估计的精度上明显优于Yule-Walker估计和CLS估计。因此，该方法对提高NGINAR(1)模型参数估计有一定参考价值。

［1］Steutel F，Van Harn K.Discrete analogues of self-decomposability and stability［J］.Ann.Probab.1979(7):893-899.

［2］Ristic M M.A new geometric first-order integer-valued autoregressive(NGINAR(1))process［J］.Journal of Statistical Planning and Inference，2009，139:2218-2226.

［3］Wedderburn R.Quasi-Likelihood Functions，Generalized Linear Models，and the Gauss-Newton Method［J］.Biometrika，1974，61(3):439-447.

［4］Lu J，CHEN Di，ZHOU Wei-xing.Quasi-Likelihood Estimation for GLM with Random Scales［J］.Journal of Statistical Planning and Inference，2006，136(2):401-429.

［5］Lin Peisheng.Efficiency of Quasi-Likelihood Estimation for Spatially Correlate Binary Data on LpSpaces［J］.Journal of Statistical Planning and Inference，2008，138(6):1528-1541.

［6］Zheng Haitao，Basawa I V，Datta S.First Order Random Coefficient Integer-Valued Autoregressive Processes［J］.Journal of Statistical Planning and Inference，2007，137(1):212-229.

［7］Zheng Haitao，Basawa I V，Datta S.Inference for Pth-Order Random Coefficient Integer-Valued Autoregressive Processes［J］.Journal of Time Series Analysis，2006，27(3):411-440.

［8］薄海玲，张海祥，张哲.INARS(p)模型的拟似然统计推断［J］.吉林大学学报，2010，48(2):219-225.

［9］Billingsley P.Statistical Inference for Markov Processes［M］.Chicago:University of Chicago Press，1961:3-6.

［10］Hall P，Heyde C C.Martingale Limit Theory and Its Application［M］.NewYork:Academic Press，1980.

［11］Klimiko L A，Nelson P I.On Conditional Least Squares Estimation for Stochastic Processes［J］.The Annals of Statistics，1978，6(3):629-642.