Y+值对地面交通工具气动阻力计算精度影响的研究
2015-12-07赖晨光任浡麒
赖晨光,任浡麒,满 超
(重庆理工大学车辆工程学院,重庆 400054)
1904年,德国人普朗特首先提出边界层的概念。在静止的空气中,假设没有气流分离现象,气流的黏性只是在物体表面大约几毫米厚的薄层中起作用,这个薄层就称为边界层[1]。由于边界层紧贴物体表面,具有黏性的流动气体使得气体流经物体表面时所产生的黏性力不可忽略。Y+是计算流体力学(CFD)中提出的一个无量纲参数。它代表第1层网格质心到壁面的无量纲距离,与速度、黏度、剪应力等因素有关系。Y+普遍存在于湍流问题中,同时对网格的划分有重要作用。合理的Y+值往往可以提高模拟计算的精度,使数值计算结果与试验数据吻合较好。于冲等[2]对Y+值对翼型气动参数计算精度的影响进行了研究,并得出结论:过大或过小的Y+值都将对某翼型的气动参数带来误差。本文采用Mira汽车模型,通过控制边界层内第1层网格的高度来控制Y+值的变化,研究不同的Y+值对数值计算结果精度的影响,并对模拟结果的变化趋势和原因进行了分析。
1 边界层区域流体流动规律
从物体表面向外延伸,边界层可依次分为黏性底层、过渡层和对数律层,近壁的流动就由这3层构成。在黏性底层中流体成层流状态,流动主要受黏性力的作用,湍流切应力几乎可以忽略。在过渡层中黏性力和湍流切应力作用相当。在对数律层中流体流动的特点和黏性底层相反,湍流切应力起主导作用,而黏性力影响相对变小[3]。由物体表面到第1层网格质心的无量纲距离Y+的计算公式如下:

式中:v为来流速度;l为物体的特征长度。美国航空航天局(NASA)便是运用雷诺数值与Y+值之间的关系来预测物体表面的 Y+值[4]。由文献[3]可知:Y+对黏性底层分界区域的影响如图1所示。在马赫数Ma=0.73,迎角α=3.19°,基于翼型弦长c的雷诺数Re=6.5×106的试验条件下,经过大量试验,大部分情况推荐Y+=11.63为黏性底层与对数律层的分界点[5]。

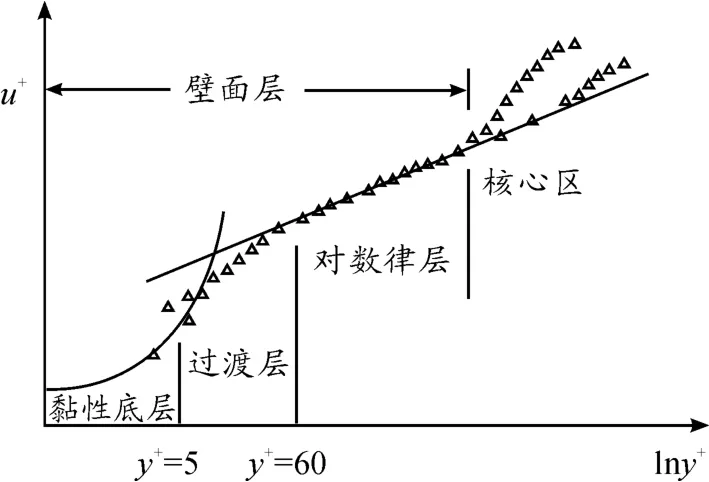
图1 边界层结构示意图
2 数字模型建立与网格划分
汽车是目前使用十分广泛的地面交通工具,而由Mira公司所提出的Mira模型包含汽车的基本轮廓特征,具有普遍代表性,所以选取Mira模型作为本次研究的模型,建立了1∶1数字模型(如图2所示),并在模型外部建立流体计算域。要求计算域的阻塞比小于8%,以减小数值模拟中风洞的阻塞效应[6],如图3 所示。雷诺数 Re=8.55 ×106。图4为划分的网格。本次研究采用了混合网格技术,在汽车模型周围建立对复杂壁面适应性较好的非结构化网格,而在远离汽车的区域选用结构化网格。结构化网格的质量相对较高,且有助于减少总体的网格数量。通过改变汽车表面第1层网格的厚度来控制Y+值的大小。本次研究共建立了15种不同Y+值对应的网格模型。通过对网格大小的调整保证网格数量相近而质量相同,以确保数值模拟计算之间的可比性。选用对地面交通工具外流场计算精度较高的Realizable k-ε湍流模型进行数值模拟计算[7]。
式中:Δy为第1层网格到物体表面的距离;ρ为流体密度;μ为流体的黏度;τw为模型表面切应力。式(1)表明:Y+值与第1层网格厚度成正比。Y+的值与运动物体雷诺数的大小有十分密切的关系。雷诺数表示流场中物体所受的惯性力和黏性力之比的无量纲参数,其计算公式如下:
图2 Mira汽车模型

图3 数值模拟计算域

图4 混合网格
3 计算结果与分析
对不同Y+值的网格进行数值计算。在FLUENT软件中得到汽车在不同Y+值下对应的气动阻力系数(CD)以及第1层网格高度 Δy,如表1所示。
对比数值计算所得到的值和试验值CD=0.3,得出计算域精确值的相对误差,见图7、8。由以上2组曲线可以得出:当Y+值为11.63时,数值计算值与风洞试验值最接近,相对误差较低,为0.023%。这从数值模拟分析层面上证明了推荐值11.63的准确性。同时,当Y+小于11.63时,计算精度并没有得到提升,相对误差反而增大。随着Y+值的逐渐增大,阻力系数CD的计算值与风洞试验值的差距呈逐渐增大的趋势。
在流场中物理量变化剧烈的地方应加大网格节点紧密排列,以提高CFD求解的精度。然而并不是越密集求解精确度越高。
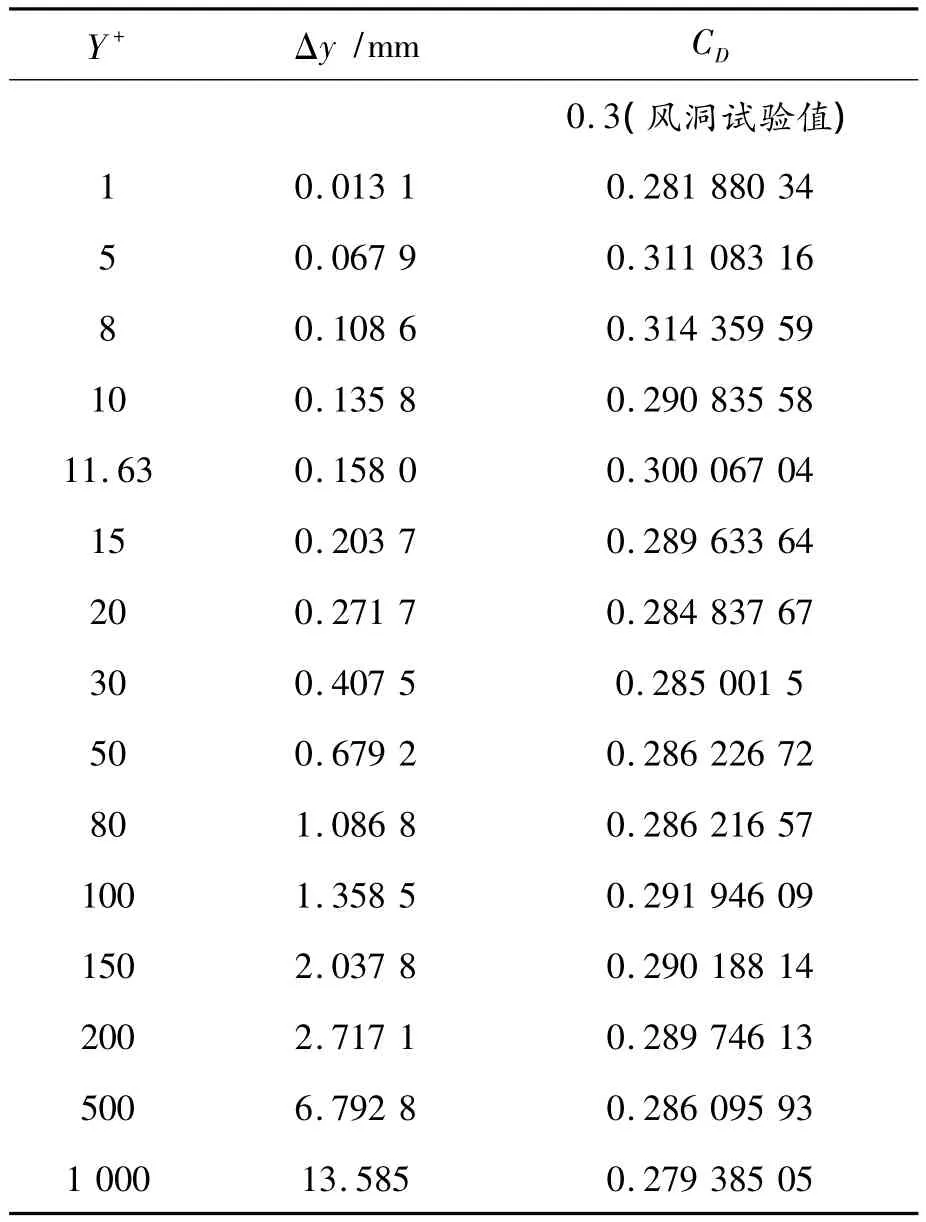
表1 Mira汽车模型数值计算结果
对于减小Y+值却无法得到更高计算精度的现象可以做如下解释:由试验数据可知此次汽车模型的雷诺数属于较高雷诺数流动。由图1可知:较小的Y+值适用于物体表面流为层流的情况。故对于高雷诺数的湍流情况[8]已不再适用,所以选择较小的Y+值并不能提高计算精度。然而,如图6和图8所示,过大的Y+值忽略了黏性底层对汽车气动参数的影响,所以同样不能提高数值分析计算的精度[2]。
如图9和图10所示,在实际流动中会存在一个随着流动方向逐渐增厚的边界层。令x为沿物体表面方向到物体表面左端的距离,当地的边界层厚度为δ时有 δ=δ(x)。对于图9所示的网格划分,网格节点位于真正的边界层之外,对于第1层网格点有Δy>δ。当在这样的网格上进行数值计算时,在固壁边界上将存在无滑移条件,即u=0。于是得到的速度坡面u将沿着y方向一直增加,如此将会得到一个边界层的形状,但是其厚度要远大于真实边界阶层。事实上,图9所示的网格划分会忽略整个物理边界层,而图中右侧所得的类似于黏性作用的速度剖面仅仅只是因为应用了无滑移的边界条件[9]。然而较小的网格厚度使Δy<δ,从而在物理边界层中存在多个网格节点,在进行CFD计算时可以有效模拟真实的边界层流动,使右部的速度剖面更接近实际流体体在边界层内的流动,如图10所示。
挑选最接近风洞试验结果的Y+值(Y+=11.63)和与风洞试验相差较大的Y+值(Y+=500)的结果进行对比分析。选取两种结果中汽车中间对称面上的压力云图作比较,如图11和12所示。由于Y+=500时对应的第1层边界层厚度大于Y+=11.36时整个边界层的厚度,故当Y+=500时网格的划分属于图9所示的网格划分策略,无法准确计算边界层内和边界层附近流体各个物理参数的变化梯度。故在Y+=11.63时汽车顶棚和后风窗玻璃的交界处出现了大梯度的压力变化,且压力最小值小于相同位置Y+=500时显示的压力变化梯度及最小值。Y+=11.63时汽车后挡风窗和行李箱盖交接区域压力增加,出现一个压力相对较高的区域,然而在Y+=500时,在同一区域中压力依旧有增加的趋势,但增加梯度小于Y+=11.63的情况。在Y+=11.63时汽车尾部到尾部后一段距离压力增加,这种趋势同样存在于Y+=500时相同区域内,但和后挡风窗与行李箱盖交接处相似,Y+=500时压力变化梯度比Y+=11.63的小。在Y+=500时汽车尾流区域出现了面积更大的压力增大区域。以与风洞试验较接近的Y+=11.63的案例为标准,可以看出在Y+=500时,在汽车后半部分以及尾流区域内,压力云图相差较大,导致计算的空气阻力系数有较大的偏差,相对误差达到4.63%。
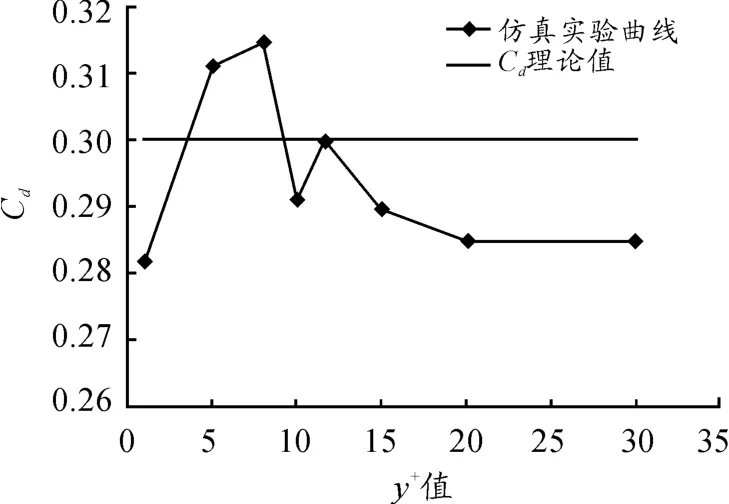
图5 Y+值较小时的CD曲线
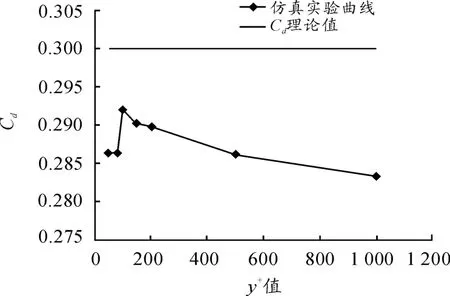
图6 Y+值较大时的CD曲线
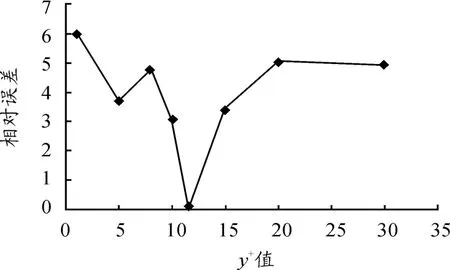
图7 Y+值较小时的相对误差
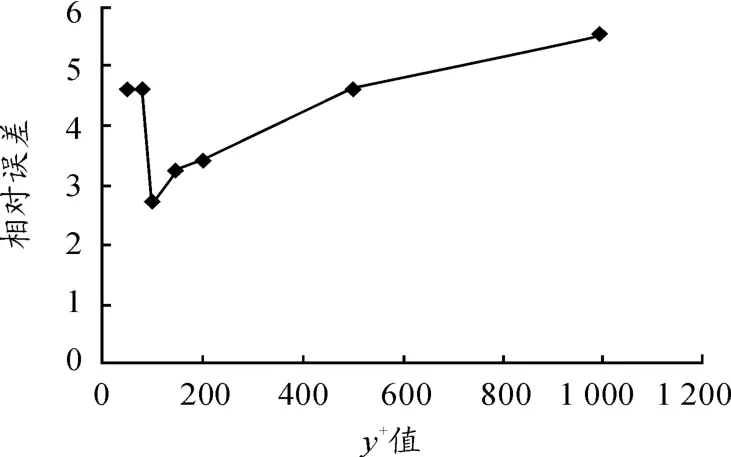
图8 Y+值较大时相对误差
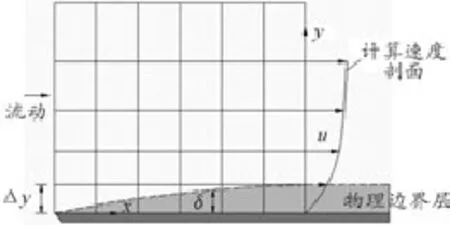
图9 Δy较大时的网格划分示意图
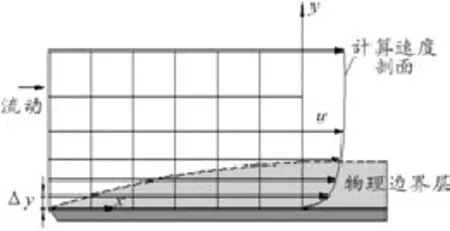
图10 Δy较小时的网格划分示意图

图11 Y+值为11.63时的压力云图

图12 Y+值为500时的压力云图
4 结论
针对Mira汽车模型的阻力系数,通过数值模拟计算验证不同Y+值对其计算精度的影响,得到如下结论:
1)当Y+值位于11.63附近时,地面交通工具的数值模拟结果与风洞试验值较为接近,随着Y+值的增加计算误差呈逐渐增加的趋势。
2)降低Y+值可以提高计算精度,但Y+值过小会降低模拟计算结果的精度。
Y+的取值将会影响到计算模型边界层的厚度,从而影响模型表面边界层气体内流动状况的捕捉。本文对Y+值的研究可为今后对地面交通工具空气动力学的数值模拟分析提供借鉴意义。
[1]傅立敏.汽车设计与空气动力学[M].北京:机械工业出版社,2011.
[2]于冲,王旭,董福安,等.Y+值对翼型气动参数计算精度的影响研究[J].空军工程大学学报,2012(3):25-29.
[3]张师帅.计算流体动力学及其应用——CFD软件原理与应用[M].武汉:华中科技大学出版社,2011.
[4]NASA美国航空航天局[2014-05-22].http://geolab.larc.nasa.gov/APPS/YPlus/.
[5]Versteeg H K,Malalasekera W.An introduction to computational fluid dynamics:the finite volume method[M].New York:Wiley press,1995.
[6]Chenguang Lai,Yasuaki Kohama,Shigeru Obayashi,et al.Influence of cooling exit flow on aerodynamic performance with different outlet layouts[J].Int J Vehicle Design,2012,59(4):331-349.
[7]刘训,赖晨光.基于Ahmed模型的外流场数值模拟[J].重庆理工大学学报:自然科学版,2013,27(9):122-127.
[8]傅立敏.汽车空气动力学[M].北京:机械工业出版社,2013.
[9]John D,Anderson J R.计算流体力学入门[M].北京:清华大学出版社,2010.
