基于加权处罚的K-均值优化算法

梁鲜，曲福恒，杨勇，才华

（1.长春理工大学 计算机科学技术学院，长春 130022；2.长春理工大学 电子信息工程学院，长春 130022）

数据挖掘（Data Mining）［1］就是从一些大量的、模糊的数据中，获取未知的、潜在有用的信息和知识的过程。聚类分析［2］在数据挖掘领域的应用最为广泛。聚类［3］属于一种无监督的机器学习算法，通过获取数据的内在属性，实现对数据的分类或压缩，使得同一类中的对象之间彼此相似，不同类中的对象之间彼此相异［4，5］。

聚类分析广泛应用于许多研究领域，如模式识别、数据挖掘、图像处理、市场研究、数据分析等。对于不同的问题和用户，国内外学者研究出许多具有代表性的聚类算法，大致分为基于层次的方法、基于划分的方法、基于网格的方法、基于密度的方法等［6］。基于层次的方法使用两种递归方式把数据对象构造成一棵聚类树，第一种是以从下到上的合并方式进行递归，第二种是以从上到下的分裂方式进行递归，该方法的聚类结果受合并和分裂操作的影响，一旦一组数据对象被合并或分裂，下一步的操作将在此基础上进行，不能进行修改。基于网格的方法把数据空间划分为有限个网格单元，以每个网格单元为处理对象，该方法比较粗放，影响聚类质量。基于密度的方法把密集区域定义为密度高于给定阈值的区域，对这些密集区域进行连接形成目标类簇，这种方法的聚类结果受阈值影响较大，处理每个样本时可能需要扫描整个数据库，引起大量的I/O操作。基于划分的方法把数据空间划分成不同的区域，每个区域表示一个数据类，计算量小，时间消耗与样本个数呈线性关系。

K-均值［7，8］是基于划分方法的代表算法，使用误差平方和SSE（Sum of the Squared Error）作为目标函数测度聚类质量，属于最小化SSE的聚类问题。K-均值算法思想简单，易于实现，其实现版本广泛应用于数据挖掘工具包中，可以通过修改算法的初始化、相似性度量、算法终止条件等部分适应新的应用环境，应用领域广泛。K-均值算法对初始聚类中心比较敏感，不同的初始聚类中心对应不同准确率的聚类结果，且得到的聚类结果不稳定易陷入局部最优。因此，怎样使K-均值算法对初始聚类中心不敏感，得到准确率高、波动性小的聚类结果，具有重要的研究意义。

为了消除初始聚类中心对K-均值算法的影响，可以通过选择不同的初始聚类中心多次执行K-均值算法，然后选择最好的聚类结果。显然，若选择初始聚类中心的次数较少，则不能保证得到全局最优解，若选择初始聚类中心的次数较多，则算法计算量较大，不适用于大数据集聚类。许多研究者对于此问题提出改进算法。例如Bradley P S等人在数据集中随机选择多个样本子集，在这些样本子集中执行K-均值算法，最后挑选出较优的初始聚类中心，对整个数据集进行聚类，但是该方法受样本子集选取方法的影响，聚类结果仅收敛到局部最优。一些研究者在挑选初始聚类中心时，引入随机算法的思想。例如CLARANS算法，通过随机选取多个初始聚类中心，比较得到的局部极小值，选出全局最优解。Likas等人使用增量的方式选取初始聚类中心，通过求解一系列子聚类的问题来解决K个聚类的问题，使用局部搜索能力得到全局优化的聚类结果，具体步骤是：首先从实现一个聚类的问题开始，选取数据集的质心作为第一个初始聚类中心，设置K=1，在此基础上，实现两个聚类的问题，设置K=2，K=1时的聚类中心默认为K=2时的第一个聚类中心，迭代地让剩余样本假设为第二个初始聚类中心，运行K-均值算法，选择目标函数SSE最小时对应的样本作为K=2时的第二个聚类中心，重复该过程直到找出K个聚类中心。该算法可以得到全局优化的聚类结果，但是计算量太大，不适用于大数据集聚类。仝雪姣等人［9］利用贪心思想根据数据的实际分布构建K个数据集合，计算K个数据集合的均值作为初始聚类中心，使得到的初始聚类中心接近算法期待的聚类中心。

对于K-均值初始聚类中心选取方法的研究已有大量的研究成果，但是没有出现公认最好的初始聚类中心选取方法。当数据集中存在噪音和孤立点时，已有的方法很难选出合适的初始聚类中心。

K-均值算法的终止条件是目标准则函数达到最小值。因初试聚类中心对K-均值算法的影响，对数据集划分形成的簇集中，有些簇的误差平方和较大，有些簇的误差平方和较小。此时，通过误差平方和较小的簇抵消误差平方和较大的簇的影响，可以使所有簇的误差平方和的累加和最小。因此，K-均值算法会把不属于同一类簇的样本划分到同一类簇中，使聚类结果偏离数据集的真实分布。每次迭代过程中，K-均值算法没有考虑到各个簇之间误差平方和的差异性，算法结束时，簇集中可能会存在平均误差较大的簇，即该簇中包含的样本属于两类或两类以上。为此，本文使用加权方案限制簇集中出现平均误差较大的簇，解决K-均值算法对初始聚类中心敏感的问题，得到全局优化的聚类结果。

1 基于加权处罚的K-均值优化算法

1.1 K-均值算法

K-均值算法是一种已知聚类个数的“无监督学习”算法。首先指定表示聚类个数的K值，然后对数据集聚类，算法结束时用K个聚类中心表示聚类结果。对于设定的目标准则函数，通过向目标准则函数值减小的方向进行迭代更新，目标准则函数值达到极小值时算法结束，得到较优的聚类结果。

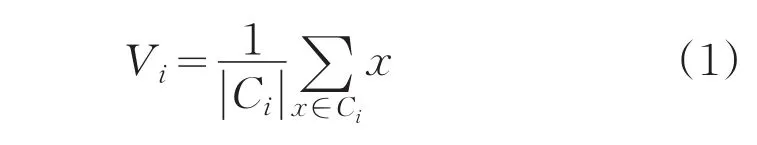
定义目标准则函数为：

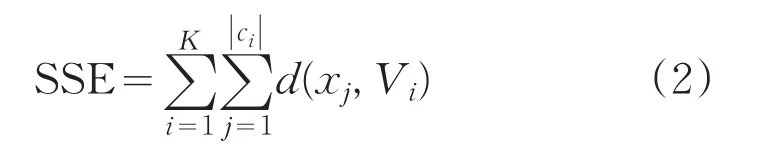
其中||Ci表示Ci类包含样本的个数，使用欧式距离

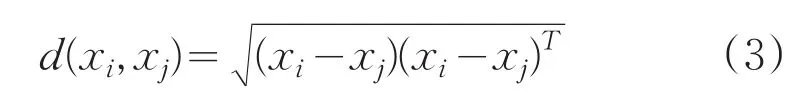
度量样本间的相似性。欧式距离适用于类内数据对象符合超球形分布的情况，目标准则函数SSE表示为每个数据对象到相应聚类中心距离的平方和，即聚类均方误差的最小值。

K-均值算法的流程如下：

（1）随机选取K个初始聚类中心V1,V2,...,Vk；

（2）按照最小距离原则，对数据集聚类，确定每个样本的类属关系；

（3）使用公式（1）更新K个簇的中心；

（4）重复执行（2）到（4），直到目标准则函数收敛或聚类中心稳定。

显然，初始聚类中心对K-均值算法产生很大的影响，簇集中易存在平均误差较大的簇，聚类结果仅能收敛到局部最优。即使选取不同的初始聚类中心执行多次K-均值算法，也只是在庞大的初值空间里进行简单的搜索，聚类结果很难达到全局最优。当数据集中存在较多噪音或孤立点时，已有的初始聚类中心优化方法很难发现合适的初始聚类中心。

1.2 基于加权处罚的K-均值优化算法

1.2.1 算法思想

由于初始聚类中心对K-均值算法的影响，聚类结果中易存在平均误差较大的簇，即簇中包含的数据对象属于两类或两类以上，聚类结果仅是局部最优。为此，在每次迭代过程中，使用加权方案对平均误差较大的簇进行处罚，给平均误差较大的簇赋予较大的权值，给平均误差较小的簇赋予较小的权值。定义处罚因子，控制对簇的处罚力度。定义加权准则函数，分配样本时，计算加权距离，把样本分到加权距离最小的簇中。这样，平均误差较大的簇将会失去一些距离簇心较远的实例，即把不属于该簇的样本划分到正确的簇中，平均误差较小的簇将会获得一些距离簇心较远但属于该簇的实例。每次迭代更新簇的权值时，引入记忆因子，控制上次迭代的权值对当前更新的权值的影响，提高算法的稳定性。以期使每次迭代过程中，都能对数据集做出正确的划分，进而使最终的聚类结果收敛到全局最优。

1.2.2 相关概念

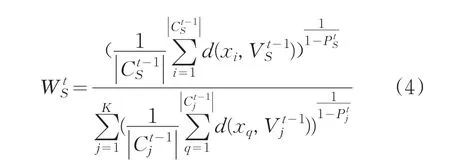
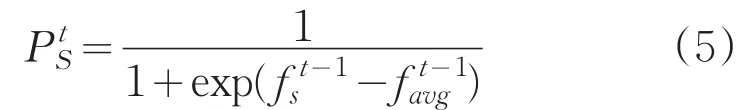
定义3为了提高算法的稳定性，在权值更新过程中添加记忆因子。设第t-1次迭代时簇S的权值为，那么添加记忆因子后，我们定义第t次迭代时簇S的权值为：

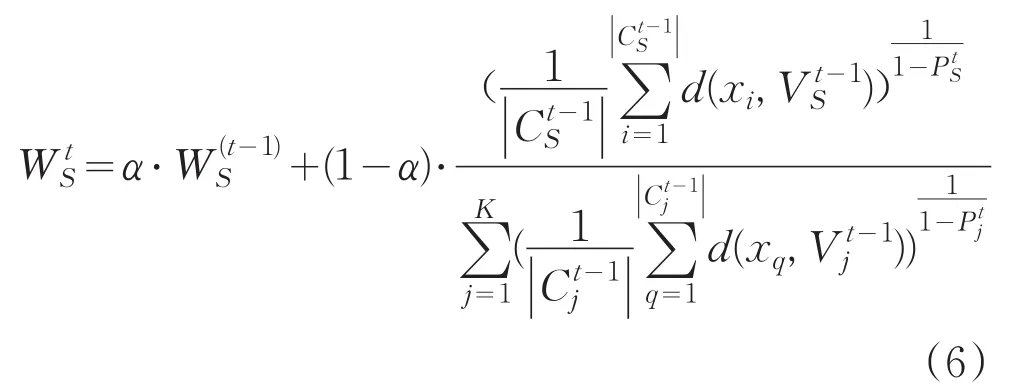
其中α是记忆因子，0≤α≤1，控制上次迭代的权值对当前更新的权值的影响。本文使用公式（6）更新每个簇的权值。

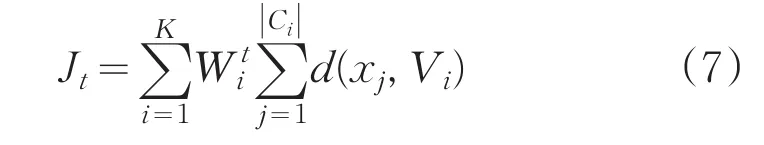
若连续两次迭代过程中，加权准则函数值的变化量小于给定的阈值ξ，则算法结束。

1.2.3 算法伪代码描述

2 结果与讨论

实验目的测试本文算法的聚类性能、抗噪性能及伸缩性。分别使用UCI机器学习数据库中的数据集，随机生成的不同规模的含有不同比例噪音的人工模拟数据集进行实验。分别使用不同记忆因子α=0下的本文算法1、α=0.2下的本文算法2、α=0.4下的本文算法3与K-均值算法、文献［9］中的算法进行实验比较。实验环境是Intel CPU，2.99G内存，931G硬盘，Windows XP操作系统，Visual Studio2013应用软件，C++作为编程语言。使用聚类误差平方和、聚类准确率，以及常用的外部评价指标Adjusted Rand Index参数对算法的性能进行评价。外部评价指标是已知分类信息的前提下对聚类结果进行评价。Adjusted Rand Index参数，用来衡量聚类结果与数据的外部标准类之间的一致程度，是Rand指数的一个变种。

2.1 UCI数据集实验

使用UCI机器学习数据库中的数据集测试算法的聚类性能，数据集描述如表1所示。分别运行不同记忆因子α=0下的本文算法1、α=0.2下的本文算法2、α=0.4下的本文算法3与K-均值算法、文献［9］中的算法各100次，比较算法的平均聚类结果。表2给出了算法的聚类误差平方和的比较结果。图1给出了算法的聚类准确率与Adjusted Rand Index参数的比较结果。

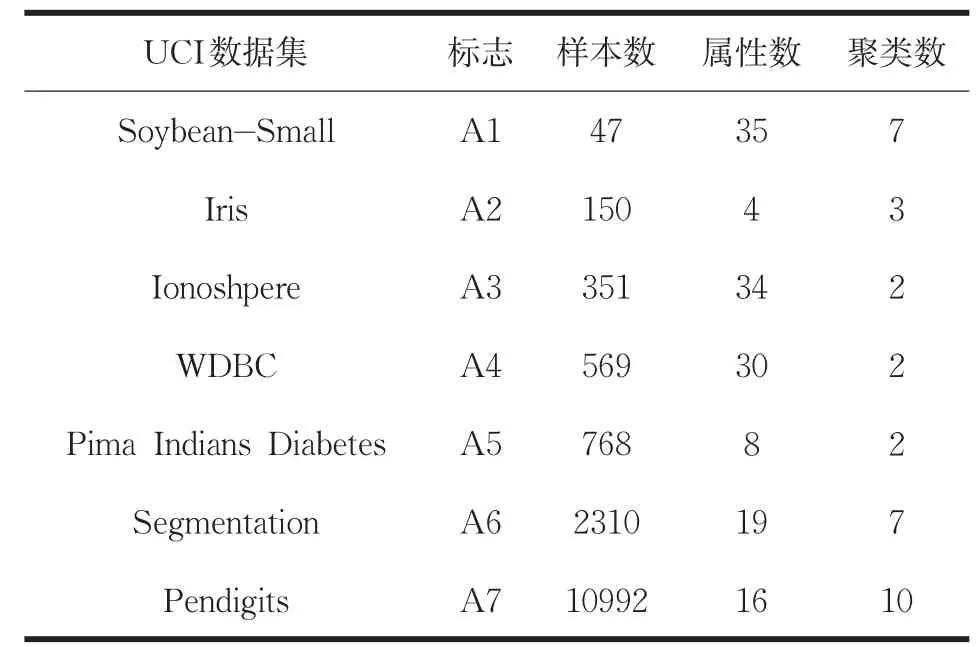
表1 UCI数据集描述

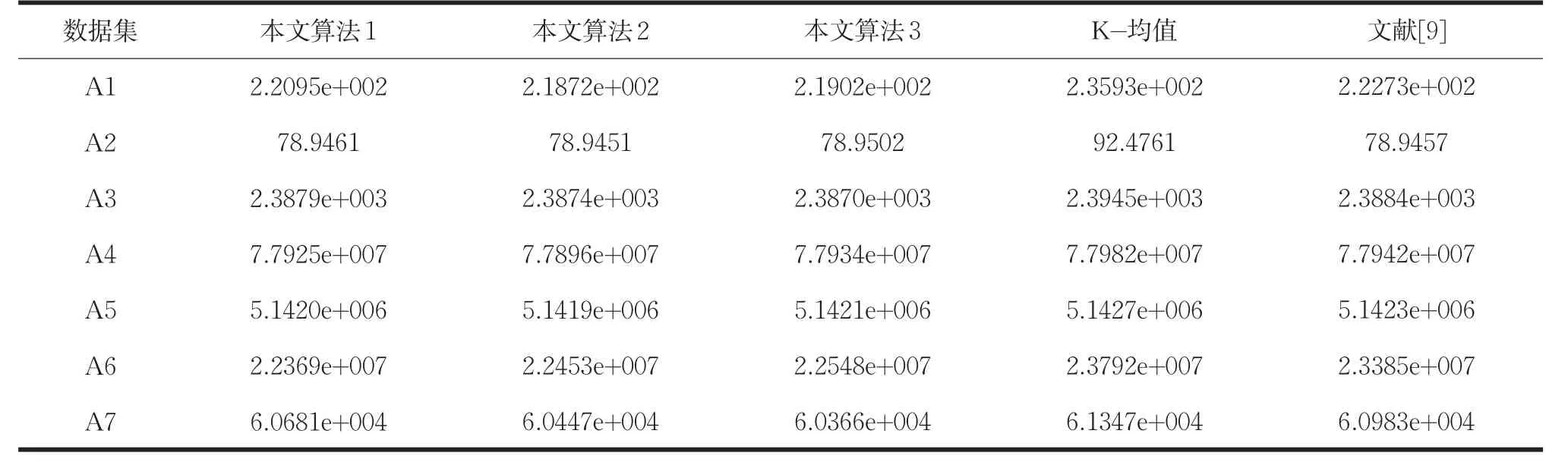
表2 UCI数据集上算法的聚类误差平方和的比较结果

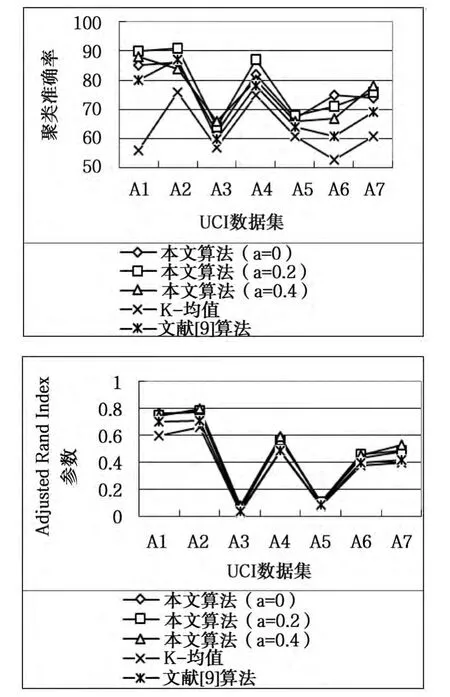
图1 UCI数据集上算法的聚类准确率与Adjusted Rand Index参数的比较

由表2可知，K-均值算法的聚类误差平方和在数据集A4（WDBC）、A5（Pima Indians Diabetes）上最优，本文算法在数据集A4、A5上的聚类误差平方和明显优于K-均值算法。文献［9］算法的聚类误差平方和在数据集A2（Iris）上最优，数据集A2上α=0.2下的本文算法的聚类误差平方和优于文献［9］算法。

图1中关于聚类准确率的比较结果可知，在所有数据集上本文算法的聚类准确率均高于K-均值算法。在数据集A2（Iris）上，文献［9］算法的聚类准确率略高（α=0，α=0.4）下的本文算法，其它数据集上均低于本文算法。图1中关于评价指标Adjusted Rand Index参数的比较结果可知，本文算法的聚类效果最好。

上述UCI数据集的实验结果表明，本文算法优于K-均值算法和优化初试聚类中心的K-均值算法，改善了K-均值算法的聚类性能，且提高了算法的伸缩性。

2.2 人工模拟数据集实验

为了测试本文算法对含有噪音数据的聚类能力，随机生成两组分别含有10%、15%、20%、25%、30%噪音的二维人工模拟数据集对算法进行测试。这两组人工模拟数据集中的样本均符合正态分布。第一组数据集包含4个类簇，样本集的规模为600。该组数据集按噪音比例由小到大排列分别为D1、D2、D3、D4、D5。第二组数据集包含6个类簇，样本集的规模为8400。该组数据集按噪音比例由小到大排列分别为S1、S2、S3、S4、S5。在10个人工模拟数据集上分别运行不同记忆因子α=0下的本文算法1、α=0.2下的本文算法2、α=0.4下的本文算法3与K-均值算法、文献［9］的算法各100次，比较平均聚类结果。表3给出了算法的聚类误差平方和的比较结果。图2是算法的聚类准确率与Adjusted Rand Index参数的比较结果。

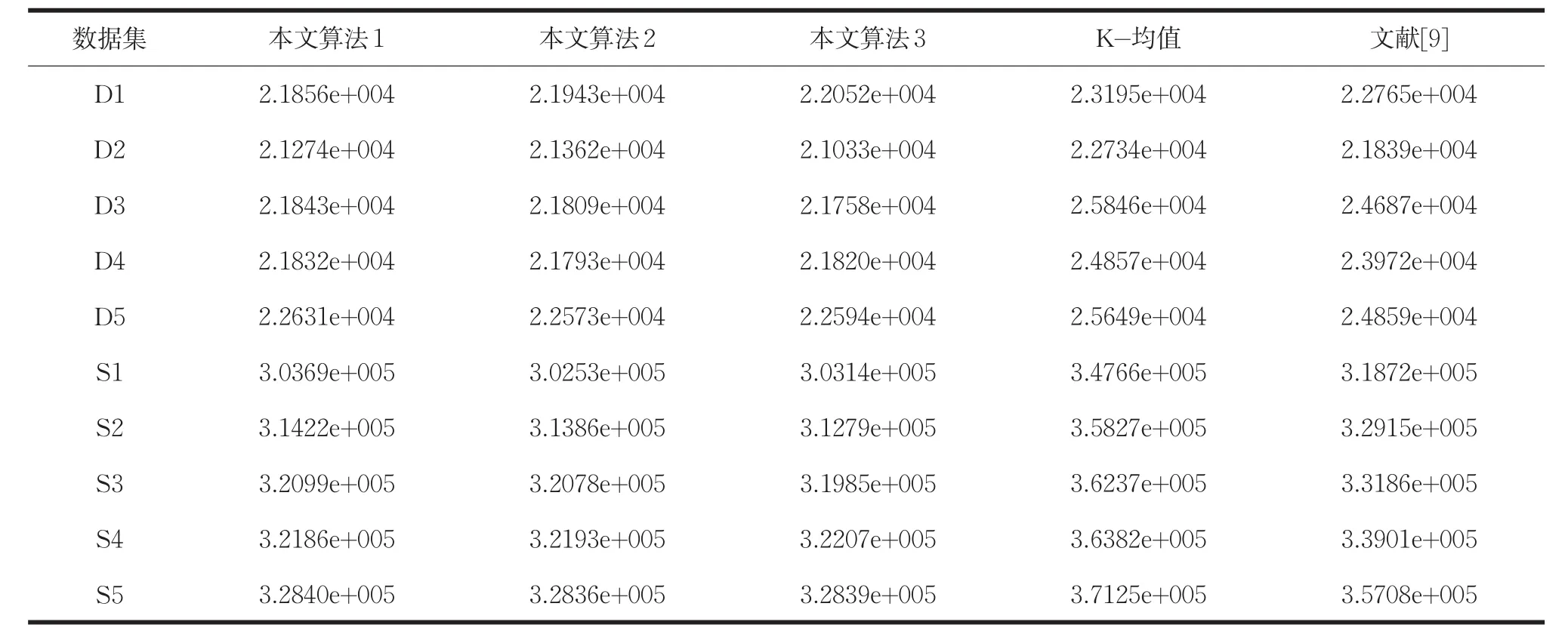
表3 人工模拟数据集上算法的聚类误差平方和的比较结果

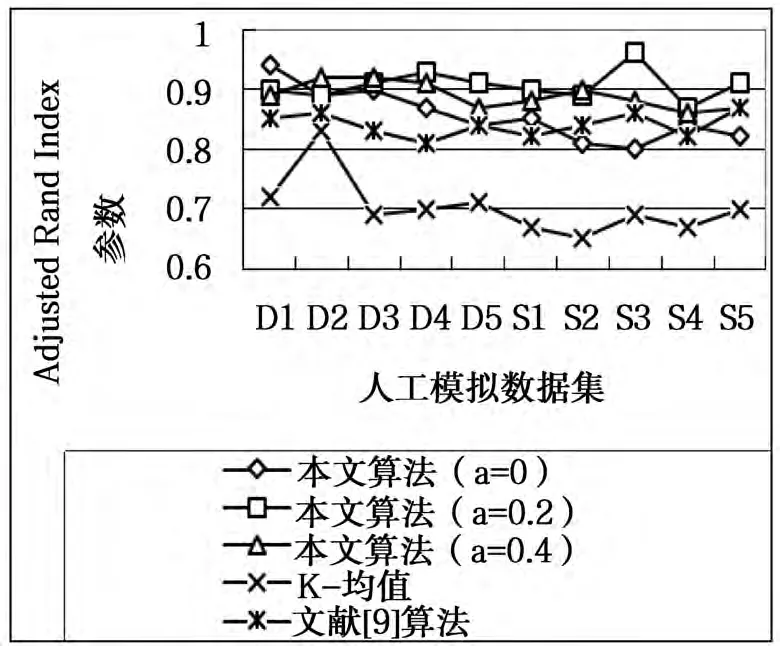
图2 模拟数据集上算法的聚类准确率与Adjusted Rand Index参数的比较

由表3可知，在随机生成的大小规模数据集上，本文算法的聚类误差平方和均低于K-均值算法和文献［9］算法。由图2可知，在随机生成的大小规模数据集上，本文算法的聚类准确率和Adjusted Rand Index参数最优。

上述人工模拟数据集的实验结果表明，本文算法在含有噪音的数据集上的聚类结果，准确率高且稳定，证明本文算法具有较强的抗噪性能。

3 结论

本文针对K-均值算法易受初始聚类中心影响的问题。每次迭代过程中，使用加权方案对平均误差较大的簇进行处罚，限制簇集中出现平均误差较大的聚簇。对数据集做出正确的划分，使聚类结果收敛到全局最优。通过UCI数据库中的数据集与人工模拟数据集的实验测试表明，本文算法具有较好的聚类性能及伸缩性，且具有较强的抗噪性能。

［1］张俊溪，吴晓军.一种新的基于进化计算的聚类算法［J］.计算机工程与应用，2011，4（24）：111-114.

［2］HanJiawei，KamberM.DataMining：Concepts and Techniques［M］.Beijing：China Machine Press，2011.

［3］张赤，丰洪才，金凯，等.基于聚类分析的缺失数据最近邻填补算法［J］.计算机应用与件，2014，31（5）：282-284.

［4］Yu H，Li Z，Yao N.Research on optimization method for K-Means clustering algorithm［J］.Journal of Chinese Computer Systems，2012，33（10）：2273-2277.

［5］韩忠明，陈妮，张慧，等.一种非对称距离下的层次聚类算法［J］.模式识别与人工智能，2014，27（5）：410-416.

［6］黄德才，李晓畅.基于相对密度的混合属性数据增量聚类算法［J］.控制与策，2013，28（6）：815-822.

［7］傅德胜，周辰.基于密度的改进K均值算法及实现［J］.计算机应用，2011，31（2）：432-434.

［8］杨志，罗可.一种改进的基于粒子群的聚类算法［J］.计算机应用研究，2014，31（9）：2597-2600.

［9］仝雪姣，孟凡荣，王志晓.对K-means初始聚类中心的优化［J］.计算机工程与设计，2011，32（8）：2721-2724.