四轴飞行器的数学模型

王震宇，熊家新，陈纯，刘丽

（长春理工大学 机电工程学院，长春 130022）

伴随着经济的发展和进步，四轴飞行器以其形体小、成本低、低环境要求、较强生存能力、省人、省物、安全方便等优势，成为各国高精尖技术的应用对象。要实现四轴飞行器的基本功能，那就要有完整的控制算法，因此需要建立四轴飞行器在低空下、近距离的数学模型，以便将四轴飞行器应用于需要它的复杂场合［1-3］。

1 四轴飞行器的飞行原理

1.1 升降控制

如图1所示，同时提高四个电机转速使飞行器上升，同时降低四个电机转速使飞行器下降。因为同时提高或降低三个电机转速会导致其姿态变化，所以一般不采取这种方式实现升降控制。

1.2 俯仰滚转控制

从理论上讲，四轴飞行器的结构是对称的，所以俯仰与滚转具有类似的控制原理。如图1所示，提高电动机M2转速时降低电动机M3转速，四轴飞行器以M1、M4所在的轴为轴，从M2向M3方向旋转。若M2为前进方向则四轴飞行器处于俯仰状态，若M1为前进方向，则四轴飞行器处于滚转状态。平稳飞行状态四轴飞行器四个电机等速转动，当某个电机转速增大时，机翼下部压强增大，促使机体做刚体旋转运动，沿前进方向是俯仰，与其垂直则是滚转运动。

1.3 偏航控制

四轴飞行器的偏航控制要比俯仰与滚转控制难度高些，想要平稳的改变四轴飞行器的航向，就要同时改变四个电机的转速。如图2所示，M1、M2、M3、M4为四轴飞行器的四台控制电机，在M1、M4逆时针转动并且M2、M3顺时针转动时，降低M1、M4转速时提高M2、M3转速，由转动惯量的惯性矩平衡原理，主机体就会按逆时针方向旋转。反方向改变转速，主机体会按顺时针方向旋转。四轴飞行器飞行时表现为航向改变。

图1 四轴飞行器俯仰滚转的控制图

图2 四轴飞行器偏航的控制图

2 旋翼的等效空气动力学模型

四轴飞行器在不同状态下动力学的系数是不一样的，如图3（a）所示，垂直飞行时，气流沿着旋翼轴向，如图3（b）所示，前进飞行时，在旋翼旋转平面和水平面成角αr，气流流过旋翼旋转平面不平行与轴向，而是斜穿过旋翼旋转平面，由此可知飞行状态不同四轴飞行器的气动特性就不同。飞行状态不同，四轴飞行器动力学系数就不同，模型也就不同，本文对四轴飞行器偏航时的旋翼受力做了简化处理，由叶素理论：四轴飞行器在偏航飞行状态，其旋翼上的力矩、力主要表现为，电机主轴的升力D、阻力E、侧向力矩F和扭矩G。由文献［2］得其求解的近似公式：

式中，p是空气密度，Α=πR2表示旋转面面积，Cr为旋翼拉力系数，CD为旋翼阻力系数，Co为旋翼扭矩系数，CR为力矩系数。旋翼的几何性状决定这些系数的大小，并且飞行姿态不同系数也会不同。ω为电机转速，由公式可知电机转速的平方与旋翼的力与力矩存在比例关系。根据控制的需要进行近似化，旋翼所受的升力为：

升力系数k由旋翼形状、尺寸与安装方式决定。

图3 旋翼与气流图示

3 四轴飞行器控制模型的建立

在建立四轴飞行器模型之前，要选取适当的空地坐标系，这样使建立四轴飞行器模型的过程相对简单，有利于分析与求解，因为四轴飞行器的速度、姿态角的大小与方向等参数是与坐标系相对应的。所以选择惯性导航中常用的两种坐标系，如图4所示，机体的XYZ坐标系与地面的xyz坐标系。前者是在四轴飞行器上固定的，X轴与前后方向的旋翼连线平行，经过四轴飞行器的几何中心正向同其前进方同向，Y轴与左右方向的旋翼连线平行，也经过四轴飞行器的几何中心并且垂直于X轴，Z轴平行于X轴、Y轴所在平面。后者是在三维空间中确定四轴飞行器位置的，四轴飞行器在哪里起飞哪里就是远点坐标，以用来确定其位置、姿态、偏航角的变化。飞机在地面刚要起飞时，两坐标系原点重合，相应的坐标轴重合。

在分析四轴飞行器运动时，采用右手坐标系［7］，那么如图4机体绕X轴旋转角为正，设机体绕X轴、Y轴、Z轴的旋转角分别α、β、γ，其中α是机体的Y轴与Z轴与地面的y轴与z轴的夹角，β是机体的X轴与Z轴与地面的x轴与z轴的夹角，γ是机体的X轴与Y轴与地面的x轴与y轴的夹角，三者分别是横滚角、俯仰角、偏航角。根据文献［7］可得到机载坐标系上的点到地面坐标系上的点的变换矩阵：

图4 飞机横滚示意图

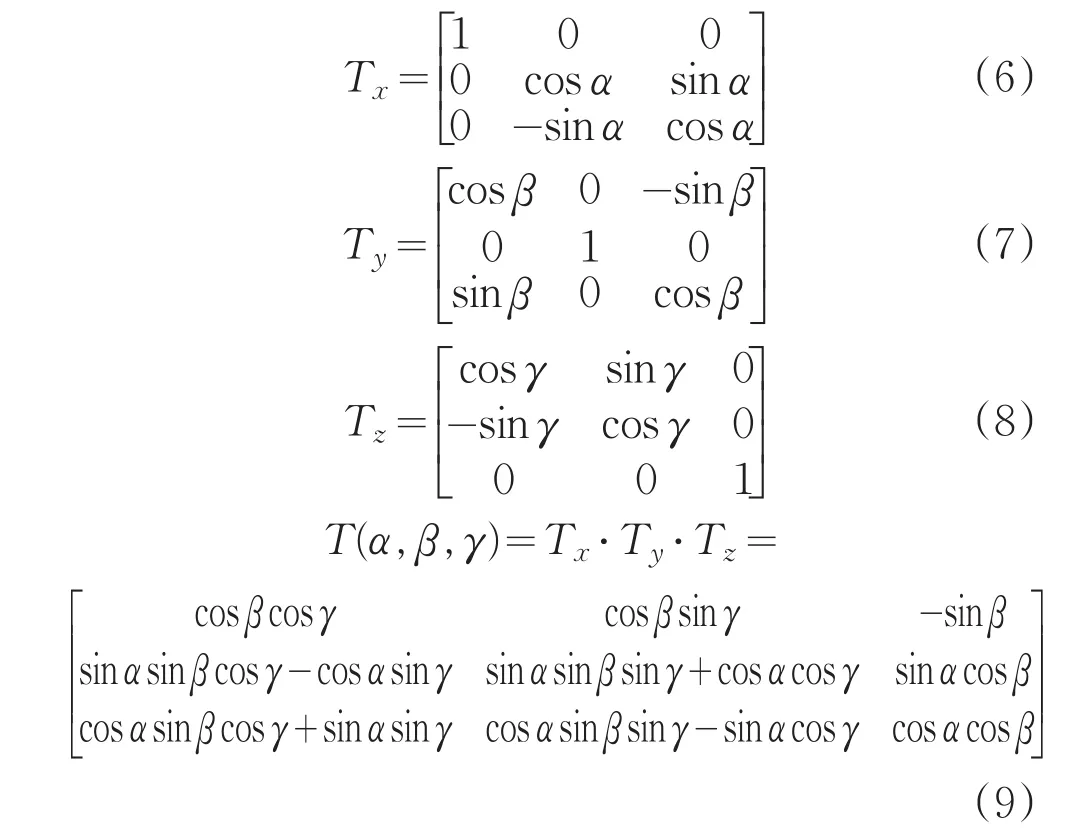
四轴飞行器控制模型的建立过程中，作出了一般性假设：四轴飞行器的质量是常数，且在其内部均匀分布；地面是惯性参考系，由于四轴飞行器在近距离、低高度飞行，所以地表近似为平面，重力加速度为常数g；不计地球自转与公转的影响；四轴飞行器的几何形状、机械结构、质量关于机载坐标平面XOZ对称，重心与几何中心重合；那么四轴飞行器的惯性矩阵为对角阵J。

忽略弹性形变与振动时，四轴飞行器在空间的运动为刚体运动，共有六个自由度，机载坐标系上的三个角运动和地面坐标系中沿轴线的三个线性运动。根据牛顿的第二定律，其动力学的方程向量表示式为：其中，作用在四轴飞行器机体上的合外力之和为F，其质量为m，其质心在地面坐标系的绝对速度为V，作用在四轴飞行器机体上的合外力矩之和为M，其在地面坐标系下绝对的动量矩为H。若在机载坐标系下，依据理论力学知识建立其运动方程，绝对导数在机载坐标系下为：

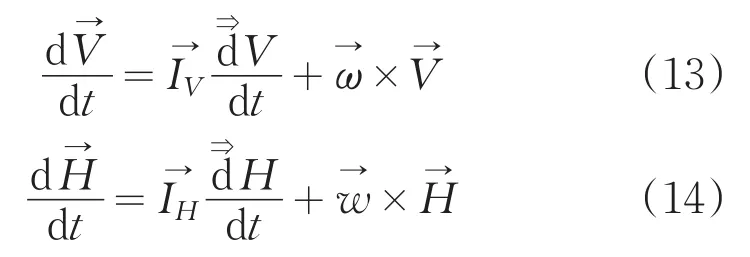
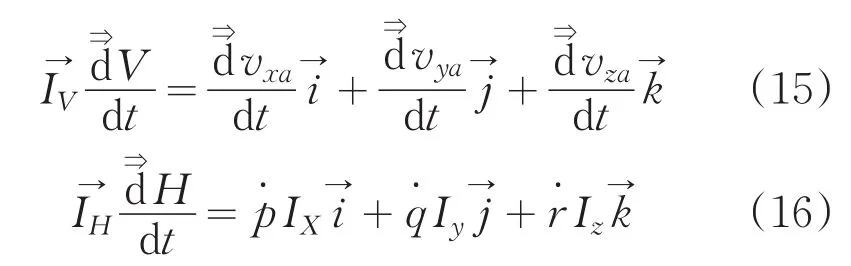
（1）线性运动方程

四轴飞行器在机载坐标系上质心的速度V→的分量为：

外力之和F在机载坐标系上的分量为：

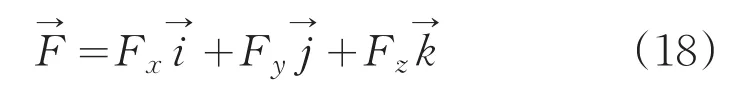
将式（13）、（15）、（17）、（18）代入（11）整理得：

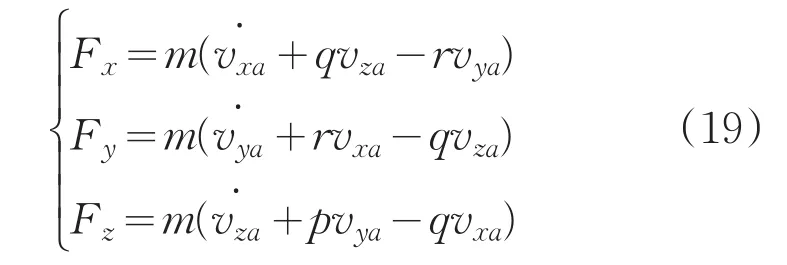
把地表坐标系的式（5）使用转换矩阵T（α，β，γ）转换到机载坐标系下并代入式（19），整理得：

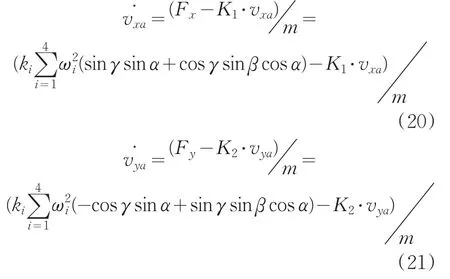
式中ki是等效的阻力系数。

（2）角运动的方程

四轴飞行器在机载坐标系上角速度的分量表示为：

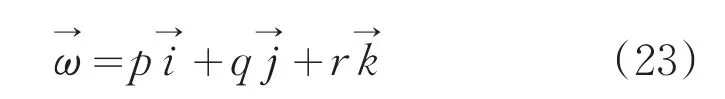
四轴飞行器机载角与机载角速度的关系：

解得机载角速度：

依据刚体的转动定律与动量矩计算的方法，式（10）及（12）解得机体的力矩方程：

式中，Mx、My、Mz为机体上和力矩 M→在机载坐标轴上的分量。类似线性运动求解，可得到角运动的方程：

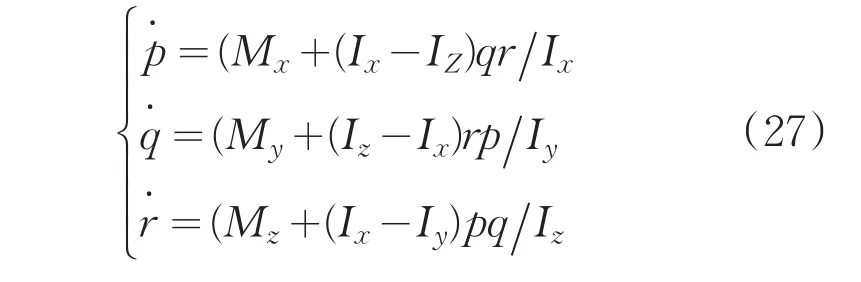
总结上述分析，得到四轴飞行器在低空近距离飞行时的运动方程：

4 仿真

本文建立了四轴飞行器仿真模型，用MATLAB的SIMULINK工具对其模型及控制器进行仿真。先用小扰动线性化方法处理式（28），根据G(s)=C(sI-A)-1B得到各通道的传递函数。由于时轴飞行器的模型的非线性与耦合性导致模型PID控制器参数参数选择困难，我们借助Signal Constraint优化工具箱来对PID控制器的参数进行自动调整［4］，仿真结构图如图5。

Kp为比例因子，K i为积分因子，Kd为微分因子，Transfer Function代表各个通道传递函数，系统的延时时间Transport Delay。在Simulink中的Output constraint优化工具，迭代仿真结果与约束条件比较，自动调节PID控制器的三个因子，直到其满足系统响应性能的指标要求。

俯仰通道传递函数：

图5 SIMULINK仿真结构图

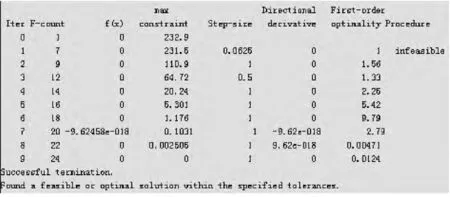
图6 俯仰通道的迭代计算过程的数据图

把传递函数代入仿真系统并输入阶跃响应得Output Constraint自动寻优工具的迭代曲线，通过优化工具得到数据图6所示，Iter为迭代的次数，F-count为函数总调用次数，加权约束Max constraint在系统的参数得到满足的仿真过程中逐渐的减少。Step size为搜索算法步长。方向导数Ditectional derivative是在寻优方向上迭代得到的曲线的变化率［6］。最后列是优化过程信息。当条件满足时提示（Successfully termination）成功收敛，且在Scope窗口输出最优曲线图7，由于对状态空间方程的小扰动线性化处理，所以控制曲线没有出现超调与振荡。

图7 俯仰通道单位阶跃响应图

用SIMULINK工具寻得俯仰通道PID控制器参数：Kp=27.13，Ki=5.61，Kd=2.39。由图7知PID控制器的俯仰通道的单位阶跃响应的稳态误差为零，上升时间和调节时间都小，因此可判断系统的动态特性良好。

5 结论

在建立了四轴飞行器的非线性的运动方程并线性化后，我们得到控制通道的传递函数，根据上述结果采用PID控制法设计各个通道的控制器，仿真结果经过一段时间都为1。这表明：四轴飞行器可以保持稳定的悬停姿态、飞行状态，所以本算法可以实现四轴飞行器控制，为四轴飞行器的进一步研究奠定了理论基础。

［1］Jason Jarrell，Yu Gu，Brad Seanor，et al.Aircraft attitude，position，and velocity determination using sensor fusion//AIAA Guidance，Navigation and Control Conference and Exhibit［C］.Honolulu，Hawaii，2008：18-21.

［2］李振波，陈佳品，张琛.低雷诺数四旋翼飞行器升力分析与计算方法的研究［J］.中国机械工程，2005，27（4）：24-31.

［3］王东平.基于嵌入式的四轴飞行器控制系统研究与设计［D］.泉州：华侨大学，2013.

［4］刘金瑶.先进PID控制及MATLAB仿真［M］.北京：电子工业出版社，2003：13-26.

［5］李文明，张涛，陈俊江.无人机载设备状态监测系统的设计与实现［J］.长春理工大学学报：自然科学版，2008，31（2）：18-24.

［6］徐昕.Matlab工具箱应用指南一控制工程篇［M］.北京：电子工业出版社，2000：167-172.

［7］童秉枢，吴志军，李学志，等.机械CAD技术基础（第三版）［M］.北京：清华大学出版社，2008：132-162.