车载激光通信稳瞄转台动力学建模与仿真
2015-12-07周鑫弘张立中洪进
周鑫弘,张立中,2,洪进
(1.长春理工大学 机电工程学院,长春 130022;2.长春理工大学 空地激光通信国防重点学科实验室,长春 130022)
随着激光通信技术的发展,空间激光通信系统在通信时要求有较高的动态跟踪与稳定精度。由于干扰力矩的存在,将影响转台的动态跟踪与稳定精度,因此建立稳瞄转台的动力学模型是十分必要的。江华等人设计的一种并联转台,基于Lagrange方法的机构动力学模型,对其动力学特性进行仿真分析,使动力学模型得到极大的简化[1]。本文利用欧拉动力学方程建立系统的动力学模型,利用ADAMS对转台进行仿真分析,为后期的试验与改进提供了理论和基础。
1 转台动力学建模
在建立稳瞄转台模型之前,需要建立坐标系以便描述其运动状态[2]。以两轴的理论中心O为基点建立转台右手直角坐标系,其中ξ,η分别为外框架和内框架的转角,如图1所示。
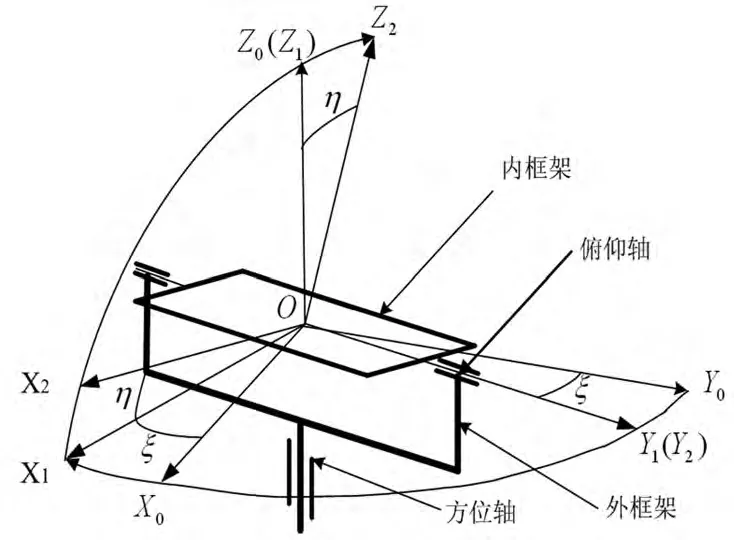
图1 建立的转台坐标系示意图
O-X0Y0Z0为载体坐标系,载体坐标系与载体固连;O-X1Y1Z1为外框架坐标系,坐标原点为O,它与转台外框架固连;O-X2Y2Z2为内框架坐标系,坐标原点为O,它与转台内框架固连在一起。
1.1 转台运动学建模
搭载平台的平动对转台的影响较小,因此可认为各个框架之间仅存在转动关系;假定推导过程各个框架和负载均为刚体,无变形量。转台的运动学建模主要是建立各框架的角速度和角加速度之间的相互运动关系,建立转台运动学建模过程如下:
1.1.1 外框架的角速度与角加速度
由于外界各种因素引起转台的平动对其跟踪与稳定精度影响较小,在建模过程中可将这些因素引起的振动整合到载体的运动中,因此可设载体坐标系O-X0Y0Z0相对于大地坐标系的转动角速度为ω0,即转台自身产生的低频扰动和外界振动对转台引起转动角速度总和:

外框架的角速度是由外框架自身角速度与载体角速度在O-X1Y1Z1坐标系内引起的扰动角速度的和值。利用坐标变换矩阵[3],
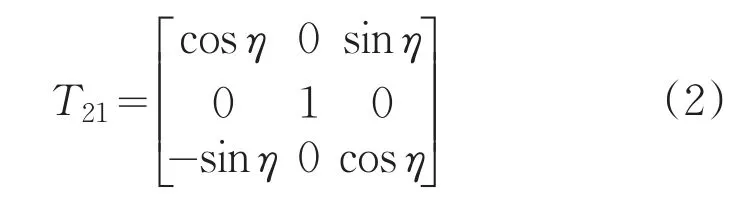
将载体角速度变换到外框坐标系中,即:

设外框自身偏转角速度向量在外框坐标系内描述为:

由式(3)和式(4)得到在外框坐标系内的外框角速度向量为:
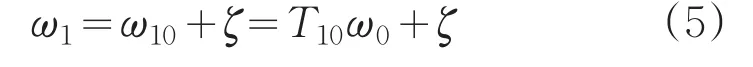
可得:
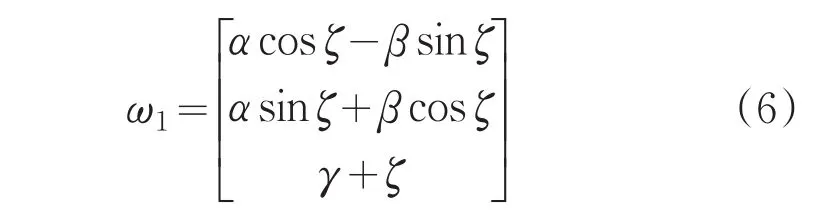
由式(6)可知,外框架角速度由载体角速度在外框坐标系的角速度分量和外框架自身偏转角速度两部分组成。
1.1.2 内框架的角速度与角加速度
利用坐标变换公式[3]
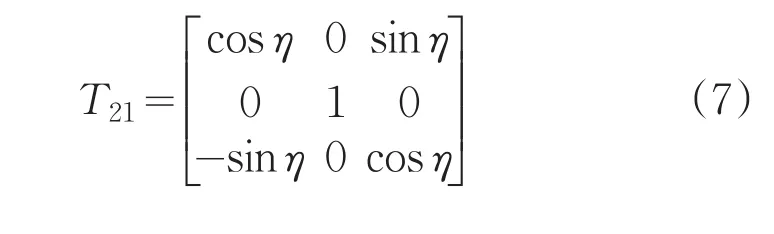
将外框架角速度式(5)变换到内框坐标系,得:
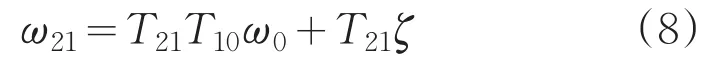
内框架在内框架坐标系内自身偏转角速度向量描述为:

由式(8)和式(9)可得在内框坐标系内的内框架角速度向量为:
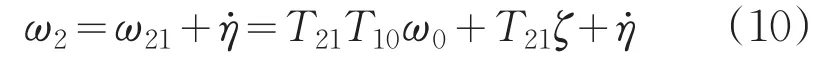
即:
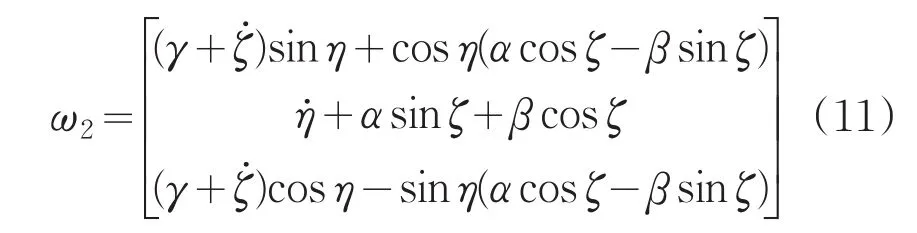
由式(11)可得,内框架角速度在内框坐标系中角速度包括三部分:一是载体角速度经过两次坐标变换投影到内框坐标系的角速度分量;二是外框架自身的偏转角速度经一次坐标变换投影到内框坐标系的角速度分量;三是内框架自身偏转角速度。
综合以上给出的在各个框架坐标系内描述的角速度的构成,其中都含有载体运动的耦合影响,载体耦合作用对视线的空间稳定产生很大影响,因此对于动基座稳定平台来说,视线稳定是最基本的控制模态,应在视线稳定的前提下进行目标跟踪。
1.2 转台动力学建模
稳定转台动力学模型主要建立各个框架的角速度、角加速度及转动惯量与电机驱动力矩、摩擦力矩、线绕力矩、耦合力矩等因素之间的关系。假设各个框架转动惯量均分布在惯性主轴上,则转动惯量阵为对角阵,即

当框架加工和安装时保证一定的精度,负载安装时调节位置或配重,则可满足上述假设。
1.2.1 内框架动力学模型建立
基于多刚体动力学中的牛顿-欧拉动力学方程,内框架的动力学公式为:

即:
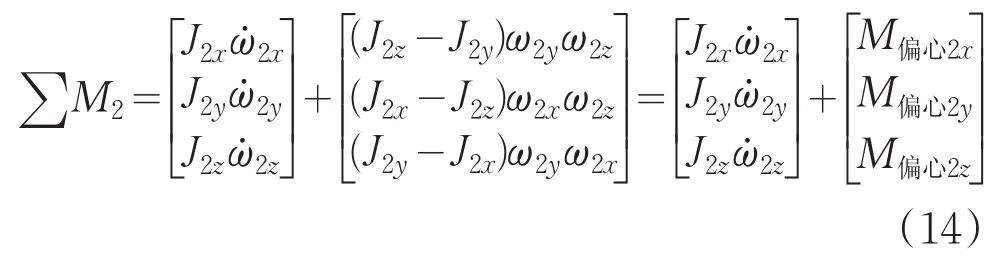

式中第二项为内框架三个主惯量矩不相等所引起的非线性扰动力矩,记为为内框合力矩向量,且有:其中:M电机2为内框架轴上的电机驱动力矩;M耦合2x和M耦合2z分别为外框架对内框架的耦合力矩在内框坐标系中X、Y轴方向的分量;M摩擦2为非线性摩擦干扰力矩;M线扰2为线缆柔性等非线性干扰力矩;M波动2为内框架驱动电机周期性波动力矩。
联立式(14)与式(15)可得内框架动力学方程式为:
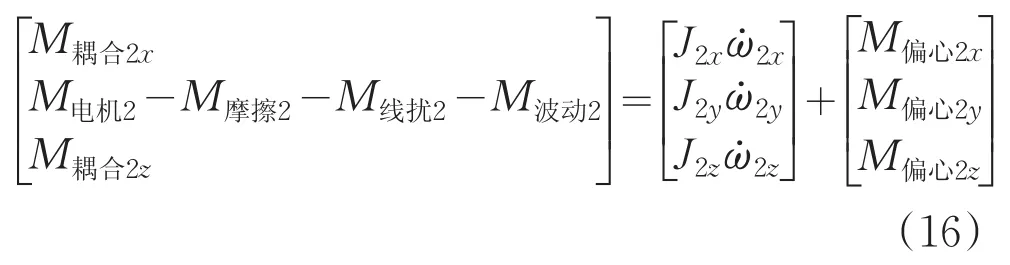
内框架只有在Y轴方向具有转动的自由度,因此只取上式中第二个分量,为了便于简化,令M摩擦2、M线扰2、M波动2三个变量和为 M干扰2,则内框架动力学模型为:
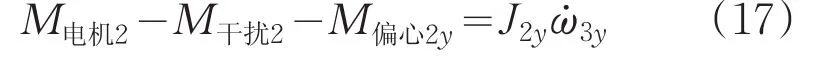
1.2.2 外框架动力学模型建立
外框架的动力学模型与内框架动力学模型建立过程和原理基本相同,只是多加了一项M21,它是内框架对外框架的反作用力矩。外框架动力学方程为:
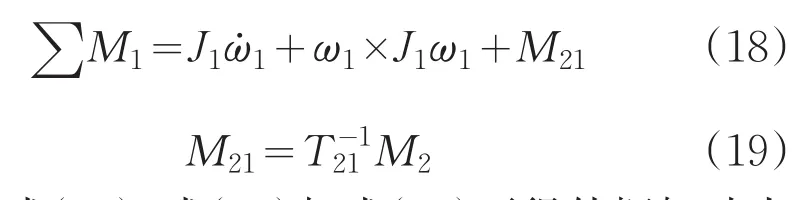
联立式(16)、式(18)与式(19)可得外框架动力学方程式为:
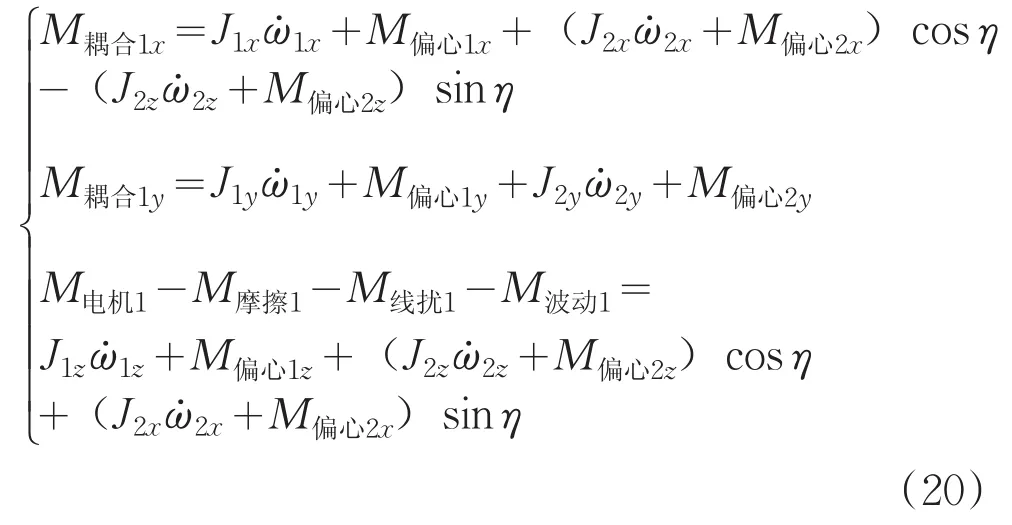
同理可知,外框架只有Z轴有转动的自由度,取式中第三个分量,令 M摩擦1、M线扰1、M波动1三个变量和为M干扰1,则有外框动力学模型为:
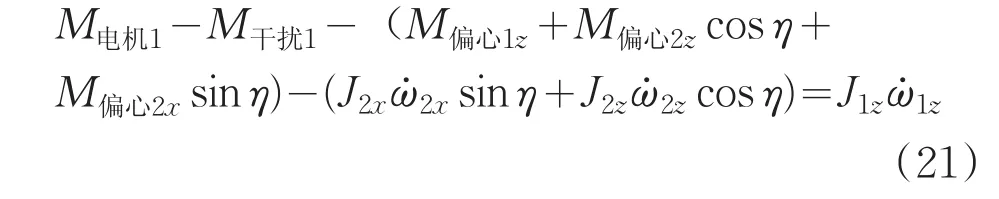
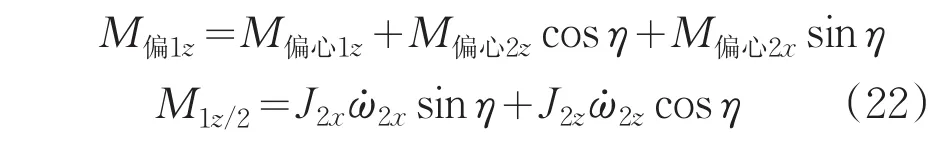
即:M1z/2为内框架对外框架的耦合作用力矩。至此,两轴稳定转台的动力学模型基本完成,即

由以上动力学模型推导过程可知:(1)干扰力矩包括非线性摩擦力矩、线扰力矩和电机波动力矩等组成,这些非线性随机干扰力矩是客观存在且无法完全消除的;(2)框架质量不平衡引起的偏心力矩,这部分扰动是由框架及载体在各个坐标系轴上的转动惯量不相等引起的,主要与框架的惯量阵、转动角速度及框架自身转角有关。应尽量使各个框架质量分布均匀且结构对称,还可以通过提高加工精度和装配精度、调整零件安装位置及配重等措施进行消除;(3)耦合力矩主要是指内框架运动对外框架的反作用力矩,且其与各个框架的惯量阵、转动角加速度及框架自身转角有关。耦合力矩是一个积累的过程,必须采取有效的解耦措施加以消除[4]。
2 转台模型仿真
依据文献[5]所提出的模型简化原则对转台模型结构进行简化。所有的简化过程都应在不改变转台结构性能、运动关系及重心位置不变为前提。简化后的模型如图2所示。

图2 转台模型简化前后对比
添加设置驱动力:在方位轴系和俯仰轴系的电机安装处添加驱动力,首先在方位电机处添加动力约束,方位轴电机以函数160d*sin(pi*time/8)进行方位旋转,其次,俯仰轴电机以函数STEP(time,0.0,0,1,-20.0d)+STEP(time,1,0.0,1.5,0)+STEP(time,1.5,0.0,2.5,20.0d)+STEP(time,2.5,0.0,3.5,20.0d)+STEP(time,3.5,0.0,8.5,0)+STEP(time,8.5,0.0,9.5,-20.0d)+STEP(time,9.5,0.0,10.5,-20.0d)+STEP(time,10.5,0.0,14,0)+STEP(time,14,0.0,15,20.0d)进行俯仰转动。
设置振动仿真的时间End time为16s(约一个运动周期),步数Steps为500:首先,将转台俯仰框架处驱动动力源俯仰电机的驱动力作失效处理,只让方位框架处电机驱动力单独的作用,此时得到外框架的角速度和角加速度曲线,如图3所示;其次,将方位框架电机处驱动力作失效处理,只让俯仰框架电机处驱动力单独作用,此时得到内框架的角速度和角加速度曲线,如图4所示;方位框架和俯仰框架的驱动电机同时运动时,得到耦合运动后外框架和内框架的角速度和角加速度曲线,如图5所示。

图3 外框角速度和角加速度曲线
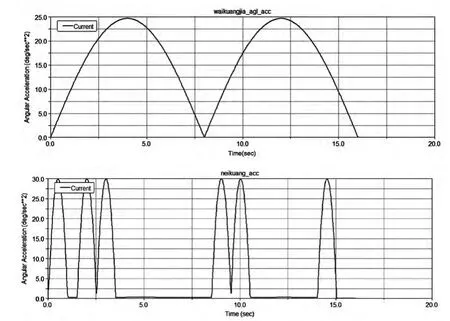
图4 内框角速度和角加速度曲线
由图3和图4可知,当方位电机和俯仰电机单独运动时内外框架角速度和角加速度曲线较平滑,说明内外框架运动较为平稳;由图5可知,当方位电机和俯仰电机同时运动时,由于方位和俯仰运动之间存在相互耦合扰动,使得内外框架的角速度和角加速度有较大程度的幅值变化,说明载体耦合作用对转台运动存在较大的影响,降低了转台的跟踪精度。因此,需要采取有效的措施消除载体运动耦合作用的影响。
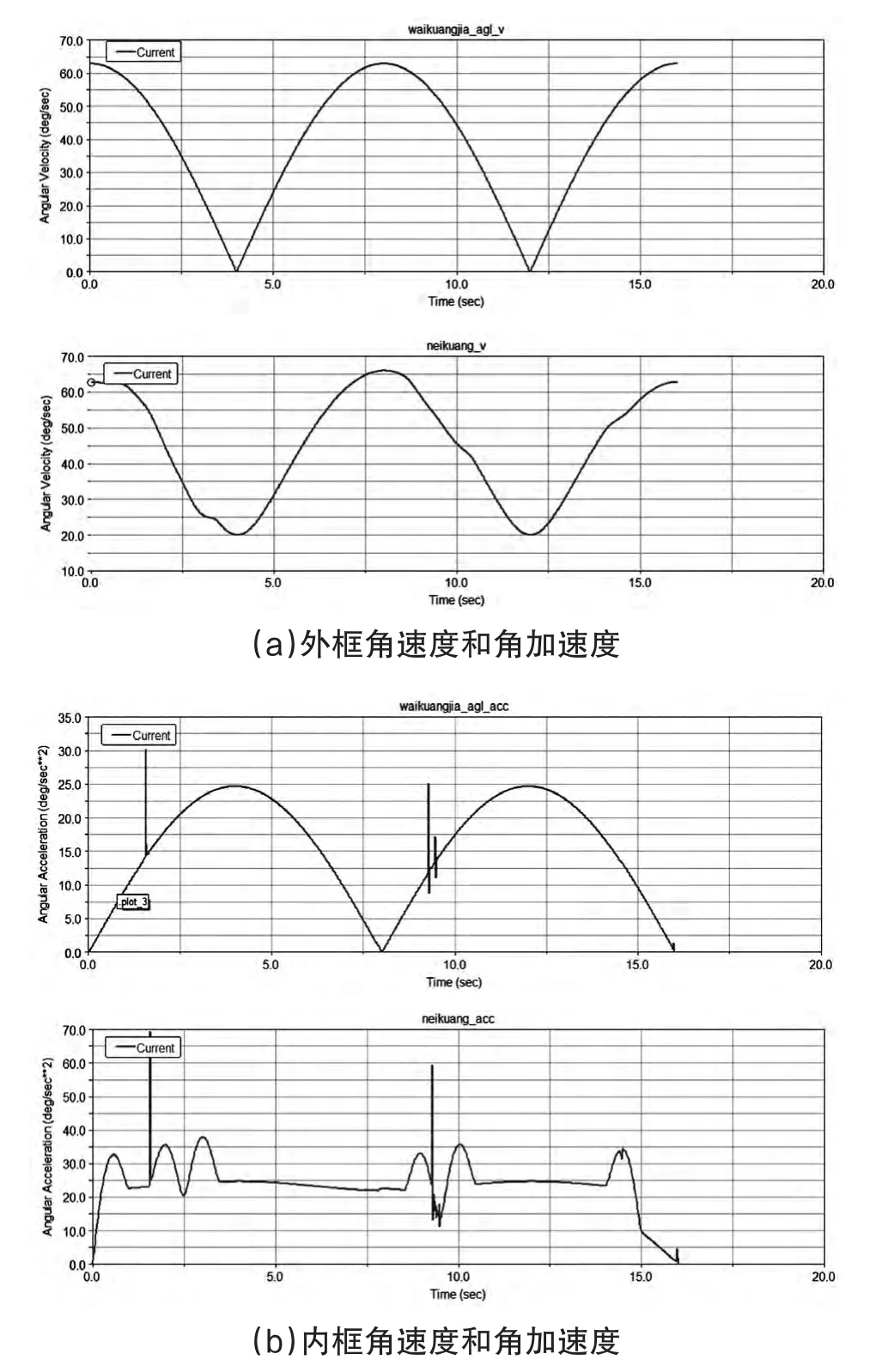
图5 耦合运动时外内框架间角速度和角加速度曲线
3 结论
从运动学与动力学角度研究了稳瞄转台的运动机理与力学特性,求解出各个框架的运动规律和载体平台的扰动对视场轴的影响以及稳瞄转台内部各框架之间的耦合力矩关系,从中看出框架自身的角速度、角加速度参数只与外层框架和载体的运动参数以及转角有关,与内层框架的运动参数无关;最内层框架不受耦合力矩影响,外层框架受内部各个框架的耦合力矩影响,体现了内部框架是外部框架的负载效应,另外,可以看出机械结构的设计与零部件的加工装配质量对稳瞄转台的性能有着重要影响,通过对转台的运动学与动力学模型分析使我们对转台内部的运动机理有个更深入理解。
[1]江华,刘利.一种2-DOF类球面并联转台的动力学建模及分析[J].弹箭与制导学报,2005(25):255-257.
[2]王耀辉.基于“DSP+FPGA”控制核心的光电经纬仪数字式控制系统设计[D]:西安:西安光学精密机械研究所,2011.
[3]李龙.车载激光通信稳瞄转台技术[D].长春:长春理工大学,2013.
[4]Kennedy P J,Kennedy R L.Direct versus indirect line-of-sight(LOS)stabilization[J].IEEE Transactions on control system technology,2003,11(1):3-15.
[5]伍建雄.新型二板式注塑机合模装置优化分析研究[D].北京:北京化工大学,2011.
