光学计算机对称三值数据海明校验研究
2015-12-07武曲吕博
武曲,吕博
(1.上海大学 材料科学与工程学院,上海 200444;2.白城兵器试验中心,白城 137001)
光学计算机的研究,尤其是“光互联-电运算”计算机已成为研究热点[1,2]。目前,光网的数据交换仍采用“光-电-光”方式,在传输过程中,存在传输损耗和数据出错的问题。而且,光学计算机中存储和运算的数据具有三值性[3],每个数据位存在三种可能的物理状态,分别由垂直偏振光、水平偏振光和无光强三个光状态表示[4],数据位众多[5]。这些特点均为数据可靠性传输带来了挑战。因此提高数据传输系统的性能和可靠性十分必要,确保光学信息在传输、存储、运算过程中的可靠性与正确性极为重要[6]。对此,王岩等[7]提出了光通信系统可靠性设计的硬件和软件方法。雷镭[8]和金翊等人[9]研究了在TOC(Ternary Optical Compute)系统监控中液晶坏位替换策略和亮暗阈值自动测定技术。这些探索性成果丰富了光学计算机数据可靠性传输研究。
在数据表示上多以对称三值形式表示光学计算机的基本数据。三值信息的可靠性存储、传输技术是光学计算机研究的热点问题。海明码由美国数学家Richard Wesley Hamming(1915年2月11日–1998年1月7日)于1950年正式提出,通过在传输的消息流中插入验证码的方法,侦测并更正单一bit错误[10]。海明规则在二值数据校验及纠错中已有广泛应用[11-13],在三值信息检验及纠错中应用也有尝试性的探讨。金翊等[4]借鉴二值海明码编码方法和分组规则,提出了一种三值海明码检错纠错原理与方法,对基于海明编码的可靠性传输方法在三值光学计算机中的应用进行了探讨,但文中对所述纠错方法并未给出解析方式表达,依赖规则表的纠错方式对纠错效率有所制约。
为更有效利用时间资源,本文基于海明树型结构讨论三值光学计算机的数据可靠性传输问题,通过分析二值数据海明纠错过程,建立三值数据与二值数据校验的联系,从解析计算角度分析了一位检测一位纠错对称三值数据的海明编码及校验规则,定义纠错因子,推导并证明对称三值数据一位纠错的解析表达式,与文献[3]中的方法相比,节省了按规则表纠错的查表时间;基于海明码树结构和纠错表达式,使纠错操作更容易由硬件运算器实现。通过实例验证了该纠错表达式的合理性。
1 二值数据的海明校验规则
1.1 二值数据单位误码检测
待传信息码Dori有lD-1位,为了对Dori在传输后进行正确性验证,设置lP位监督码(即校验码)P,使Dori的各个位Dd和P的各个位Phier按一定规律交叉排列。将Dori与P组成的数位串称为lH-1位的海明编码,记为Hamming( )lH-1,lD-1,其中,为海明码码长,
lD-1为信息码码长,lP为监督码码长:

传输后,Hamming( )lH-1,lD-1的lH-1位中出错位在1位以下(包含1位)的情况有lH种可能[14]。有一种可能是传输后的Hamming( )lH-1,lD-1是正确的,有lH-1种可能是Hamming( )lH-1,lD-1中的某一码位出错,错误可能出现在信息码Dori中,也可能出现在监督码P中。lP位的监督码P可以表示 2lP种出错位在1位以下(包含1位)的情况[15,16],
因此:


现有研究中,通常将该函数关系规定为异或运算。异或运算是基本逻辑运算“与运算”and(A ,B )、“或运算”or(A ,B )、“非运算”not(A)的组合,如式(4)。
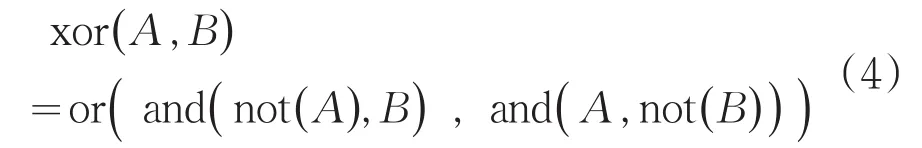
二值逻辑的异或运算相当于不考虑进位时的算术加/减运算。令add表示无进位加运算,∑表示连续的add运算,则式(3)可表示为如式(5)的形式。

校验传输后数据的实质是比对监督码P各码位传输前后的值是否相等。通常也将该环节计算规定为异或运算,其计算本质是对二者进行无借位减法运算。以sub表示无借位减法运算,Cx表示监督码的Px码位传输前后的差异,并将其定义为相对校验位,其与 vpx和的函数关系如式(6)。
3.扎实推进留守儿童德育教育工作,使其接触到的文化生活日渐丰富。学校应该根据留守儿童的实际情况,开展多种多样的活动,让其可以真正参与进来;制订留守儿童读书计划;设立亲情电话;为留守儿童宿舍安装闭路电视;按时向留守儿童开放微机室,代理家长及时指导孩子上网学习。
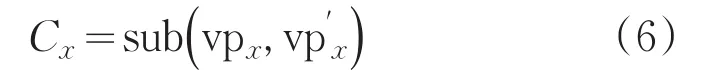
图1为文献[17]建立的适用于校验二值数据的二叉树结构的海明树,其叶结点为由信息码D各位和监督码P各位编码组成的海明码H,如式(7),当logh+12为整数时,H0,h为监督码位,否则H0,h为信息码位。

将H划分为NiVstep个交集为空的校验集合Vi,j,每个集合包含i+1个元素。图中Vi为校验运算,表示从校验集合Vi,j中判断是否有1位出错位,记为Vi:Vi,j|1,i≥0。Vi,j包含 i+1个 H0,h,j∈[ )
0,NiVstep,经过NiVstep步Vi计算后,可定位H中出错的码位,其中:

当i>0时,令Vi运算的操作数是2个同级计算Vii的运算结果,即Vi可以成Vii的函数:Vi=V1( )
Vii,其中i>ii≥0。一般地,当 i可以表示为如式(9)所示的hier函数时,在结束校验H的全部码位之前,有式(10)成立。特别地,海明树的深度与海明码数据位数满足式(11)的关系。
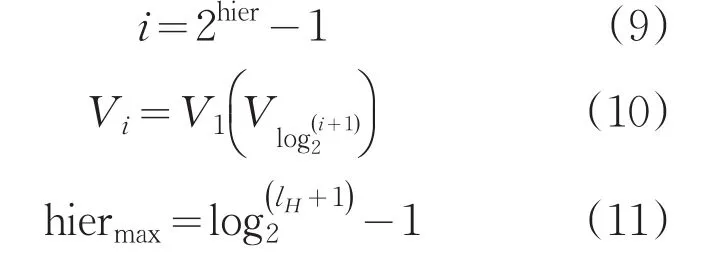
计算某监督码位Px值的若干信息码位Dy归属同一校验集合Vi,j,其各分支标识的权值(0或1)对应各相对校验位Cx可能的取值。
传输后,根据式(6)计算得到各相对校验位的值,基于图1,选择与lH相匹配的结点作为错误定位出发的根结点,以Cx值为向导寻访到叶结点,定位出错码位,由该根结点到该叶结点所经历的相对校验位Cx组成了错误定位路径,记为RC。
1.2 二值数据单位误码纠错

由于某一位出错时其错误定位路径RC中必有相对校验位不为0,且不为0的相对校验位总是只等于1,因此,RC中最接近叶结点层的非零相对校验位的值Clast即是纠错因子Ccorrect的值。
2 对称三值数据的海明校验规则
2.1 对称三值逻辑运算
对称三进制(symmetric ternary)以 1ˉ,0,1表示数据[18]。其中表示以0为中心的与1对称的-1。其逻辑与运算and(A ,B )、逻辑或运算or(A ,B)、逻辑非运算not(A) 规则如表1、表2、表3[19,20]所示。

表1 对称三值与运算

图1 用于二值数据一位检测一位纠错的海明树

表2 对称三值或运算

表3 对称三值非运算
由表1、表2可以看出,只要操作数中出现过0,按式(4)进行异或运算,其结果恒为0,因此,需要从算术运算角度研究对称三值信息的海明校验规则。
2.2 对称三值与二值逻辑
若传输前后海明码中未有码位出现改变,则所有相对校验位Cx均为0;否则,会出现某个(某些)Cx为1ˉ或1。虽然Cx的值有三种可能,但传输信息正确与否的结论仍然具有二值性:出错、未出错。因此,图1海明码树仍适合于三值海明信息校验。
对称三值数据海明校验时出错的码位可能有两种情况,错误值可能在中心值0两侧的任意一侧,可以认为是比原值少1或多1。因此,为了在检测到错误码位时直接获得纠错因子,需要在海明码树中保留是哪种情况的出错:1ˉ或1,对图1的海明码树进行分支扩展,如图2所示。由此可知,对称三值数据海明校验仍可以采用海明二叉树结构,只是指明错误的分支具备两个权值:1ˉ和1。
基于图2所示的海明树对对称三值表示的信息进行校验,若海明码所有码位均传输正确,则RC中每个相对校验位Cx均为0,由其组成的定位路径为全0,错误位被定位在H0,0;否则,RC中将出现一个或多个Cx值为1ˉ或1,错误位即可被准确定位。
2.3 纠错表达式通用性证明
定位错误码位的过程是由图2所示的海明码树的根结点按各Cx的值选择相应路径访问至该码位所在的叶子结点,且RC中的各非零Cx值总是保持符号一致,即或全为1ˉ,或全为1。
证明:
对于任一监督码位Px,传输前值为vpx,传输后值为 vp′x,其值由式(13)计算得到,其中 vdy和vd′y分别表示信息码位传输前后的值,且以式(14)为条件。

若传输后某一信息码位Dy出错,相对校验位Cx的值由式(15)计算得到。

由于假定前提为传输后至多有一位出错,因此

图2 对称三值数据一位检测一位纠错的扩展分支海明树
对任一Dy必有:

若传输后信息码位均正确,有且只有某一监督位Px出错,则Cx的值由式(17)计算得到。
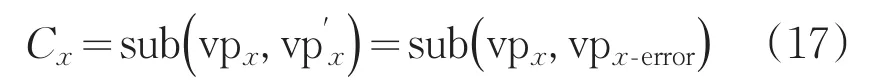
对任一Px必有:
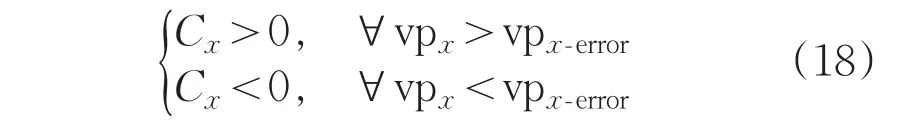
即当传输后某一数据出错时,无论该位为信息码位或监督码位,错误定位路径RC中所有非0的Cx值符号均一致。
因此,纠错因子式Ccorrect在对称三值数据纠错中仍然有效,纠错表达式式(12)仍然成立。对称三值数据无进位加法add( )A,B规则如表4所示。

表4 对称三值无进位加运算
3 计算实例
设待传数据由对称三值信息码表示为Dori=11ˉ0101ˉ1011ˉ0 ,增设虚拟位 D-1并编码后生成海明码Hamming( )16,12,D与P在海明编码中的位置及取值如表5所示。

表5 海明码Hamming( )16,12:H0,h
由式(13)可计算各监督码位传输前的值vpx。


表6 任一海明位H′0,h的纠错
4 结论
本文通过对二值数据一位检测一位纠错的海明规则的分析,以及对对称三值数据逻辑运算特点的研究,建立了二值逻辑判断与三值逻辑计算的联系;通过对二值数据校验海明树进行分支扩展,确定对称三值数据校验的海明树结构;引入纠错因子,推导并证明了二值、对称三值数据通用的一位检测一位纠错表达式。该纠错方式与文献中按规则表纠错的方式相比,节省了查找规则的时间,以基本加法计算实现纠错,使纠错运算更容易由硬件运算器实现。实例计算表明,分支扩展后的海明码树与纠错表达式具有合理性,适用于对称三值数据的单位检测单位纠错,可以在一定程度上保证三值光学计算机在这一特定数据表示形式下的数据可靠性传输。
[1]李梅.三值光计算机研究综述[J].电子设计工程,2014,22(17):22-25.
[2]王先超,姚云飞,孙道德,等.三值光学计算机中运算请求调度[J].计算机工程与应用,2012,48(25):42-47,104.
[3]Shen Yunfu,Pan Lei.Principle of a one-step MSD adderfora ternary opticalcomputer[J].Science China Information Sciences,2014,57(1):012017.
[4]金翊,何华灿,吕养天.三值光计算机的基本原理[J].中国科学(E辑),2003,33(2):111-115.
[5]金翊,欧阳山,宋凯.三值光学处理器的数据位管理理论和技术[J].中国科学(信息科学),2013,43(3):361-373.
[6]沈云付,潘磊.扩展三值纠一检二码原理与设计[J].电子学报,2013,41(8):1615-1621.
[7]王岩,杨奇峰,贾琪,等.空间光通信系统可靠性设计与实现[J].微电子学与计算机,2010,27(9):12-15.
[8]雷镭,金翊.三值光学计算机解码器亮度阈值自动测定技术[J].计算机工程与设计,2012,33(1):233-237.
[9]金翊,顾莹莹,左开中.三值光学计算机解码器的理论,技术和实现[J].中国科学(信息科学),2013,43(2):275-286.
[10]Hamming R W.Error detecting and error correcting codes[J].The Bell System Technical Journal,1950,29(2):147-160.
[11]Neuberger G,De Lima F,Carro L,et al.A multiplebitupsettolerantSRAM memory[J].Acm Transactions on Design Automation of Electronic Systems,2003,8(4):577-590.
[12]Carlos Munuera.Hamming codes for wet paper steganography[J].Designs Codes and Cryptography,2015,76(1):101-111.
[13]Md.Shohidul Islam,Cheol-Hong Kim,Jong-Myon Kim.A GPU-based(8,4)hamming decoder for secure transmission of watermarked medical images[J].Cluster Computing-The Journal of Networks SoftwareToolsand Applications,2015,18(1):333-341.
[14]阎华,范宇.差错控制编码技术应用研究[J].航空兵器,2005(4):30-34.
[15]Bernard Sklar.Digital Communications Fundamentals and Applications Second Edition[M].Pearson Education Limited;Pearson New International Edition,2013.
[16]唐朝京,雷菁.信息论与编码基础[M].北京:电子工业出版社,2010.
[17]Wu Qu,Lv Bo,Wang Lei,et al.Hamming code specification analysis based on binary tree[EB/OL].北京:中国科技论文在线[201409-174].
[18]左开中,金翊,严军勇.三值光计算机的数值表示及其基本算法[J].计算机技术与发展,2007,17(9):8-10,14.
[19]姚从军.三值逻辑的思想和方法[J].北京理工大学学报:社会科学版,2010,12(1):127-131.
[20]马明辉.三值逻辑与意义理论[J].西南大学学报:社会科学版,2015,41(1):21-28.
