非对称缸气液联控伺服发射系统模糊-PID控制研究

练永庆，郭 煜，田 兵

(1.海军工程大学 兵器新技术应用研究所，湖北 武汉430033;2.海军装备研究院，北京100161)

0 引 言

为了消除和降低舱内排气噪声，许多国家都致力于研制新型的低噪音鱼雷发射装置，液压蓄能式鱼雷发射装置就是其中之一［1］。液压蓄能式发射装置属于非对称缸气液联控伺服发射系统［2］，该系统控制阀阀口的非线性、气腔内热力过程的复杂性以及相对于驱动力较大的摩擦力，都决定了非对称缸气液联控伺服发射系统具有较强的非线性。本文主要在非对称缸气液联控伺服发射系统控制策略研究基础上，进行了该系统模糊控制器的设计，并对该系统在多种典型输入信号条件下的PID和模糊-PID控制过程进行仿真研究与分析。

1 非对称缸气液联控伺服发射系统简介

1.1 系统组成及工作原理

非对称缸气液联控伺服发射系统［2］的结构如图1所示，系统由气液缸、负载、传感器、计算机、控制器、高速开关阀及其驱动电路组成，采用PWM脉宽调制方法对高速开关阀进行控制。

非对称缸气液联控伺服发射系统的基本工作原理是:传感器采集的信号与给定的信号相比较，得出偏差信号，经过控制算法计算，计算机发出PWM控制信号控制液压高速开关阀的启闭，使得系统向着减小偏差的方向运动，从而实现负载位置、力的伺服控制。

图1 非对称缸气液联控伺服发射系统原理及参数示意图Fig.1 Principle sketch asymmetric cylinder pneumatic hydraulic combination control servo launching system

1.2 系统数学模型

系统数学模型主要包括:气体状态方程、液腔流量连续性方程、高速开关阀流量方程、系统力平衡方程、非对称缸气液联控伺服发射系统状态方程等，具体可参见文献［2］。

1.3 非对称缸气液联控伺服发射系统状态方程

根据系统数学模型，运用线性化理论对气液缸在平衡点附近作线性化处理，并进行拉氏变换，可得到有源非对称缸气液联控伺服发射系统状态方程为:

2 非对称缸气液联控伺服发射系统模糊控制器设计

根据模糊控制器设计基本步骤［3］进行非对称缸气液联控伺服发射系统模糊控制器的设计，该控制器以位置(或速度)误差E、误差变化EC为输入，控制量为输出的二维模糊控制器。

1)误差E、误差变化EC 以及控制量U的模糊集

误差E 及误差变化EC的模糊集取为{负大，负中，负小，零，正小，正中，正大}，即

由于液压高速开关阀的控制量只能取［0，1］，因此其模糊集取为{零，小，中，大}，即

2)模糊集的隶属度函数

非对称缸气液联控伺服发射系统模糊控制系统采用三角形隶属函数，如图2所示。

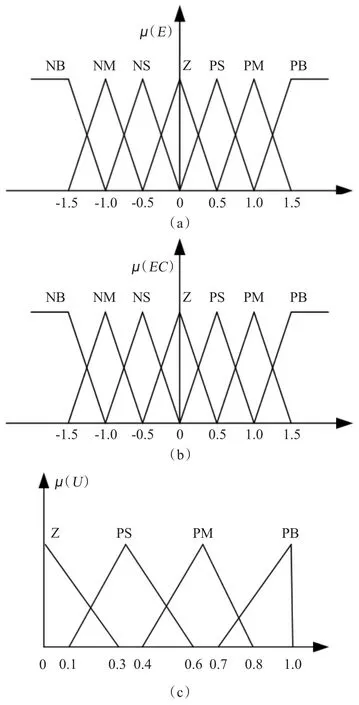
图2 隶属函数Fig.2 Membership function

3)模糊控制规则的建立

通过大量仿真分析，建立非对称缸气液联控伺服发射系统的模糊控制规则如表1所示。

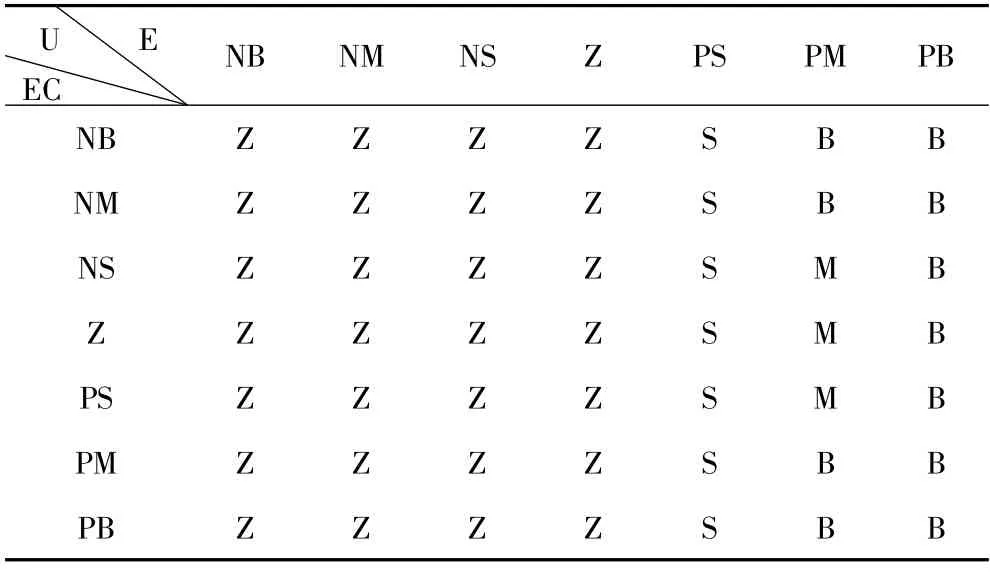
表1 非对称缸气液联控伺服发射系统模糊规则Tab.1 Fuzzy ruler of acphccsls

4)模糊推理

采 用 Mamdani法［4］进 行 模 糊 推 理，根 据Mamdarin法可得到控制量U的模糊集合为:

式中，w1=μA1(E0)∧μB1(EC0)，E0为采样得到的误差，E0∈A1，E0∈A2，EC0为误差变化，EC0∈B1，EC0∈B2，μA1(E0)为A1隶属度，μB1(EC0)为B1隶属度，“∧”为取小运算;w2=μA2(E0)∧μB2(EC0)，μA2(E0)为A2隶属度，μB2(EC0)为B2隶属度，“∨”为取大运算。

5)解模糊

采用重心法进行解模糊。重心解模糊器所确定的清晰量x*是模糊集F的隶属度函数所涵盖区域的重心［5］，即

式中:μF(x)为模糊集F的隶属度函数;∫V为常规积分;V为积分区域。

如果将μF(x)看做是一个随机变量的概率密度函数，则重心解模糊器给出的就是这个随机变量的均值。有时应消去那些在F 中的隶属度值太小的x∈V，这使得重心解模糊器变为:

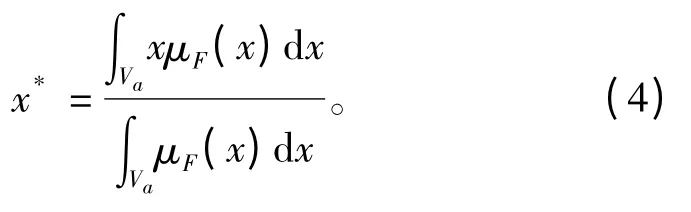
3 系统控制过程仿真

3.1 仿真模型及参数设置

由于非对称缸气液联控伺服发射系统是非线性系统，其状态方程见式(1)。现以系统的非线性方程为对象，采用不同的控制方法进行典型信号跟踪性能仿真，其仿真Simulink 框图如图3所示。模糊-PID控制采用模糊-PID 开关切换控制器，当误差量大时采用PID控制，当误差量小时采用模糊控制。

图3 系统控制仿真框图Fig.3 Simulation block diagram

仿真参数设置:

A1=0.125 7 m2(缸径0.4 m)，A2=0.117 8 m2(活塞杆直径0.1 m)，p10=0.5×106Pa，V10=0.07 m3，M= 1 000 kg，kq=0.1，kp=1 ×10-6m3/Pa·s。

由于系统没有回程控制，即系统速度在运行过程中总是大于0，因此在典型信号响应的输入选择时:对于位移量选择阶跃及斜坡信号;对于速度量选择阶跃、斜坡和大于0的正弦信号(正弦信号与同幅值的阶跃信号的叠加信号)。

3.2 仿真结果

系统控制过程仿真结果如图4和图5所示。图4为系统PID控制的典型输入信号跟踪仿真结果，图5为系统模糊-PID控制的仿真结果。

图4 系统PID控制结果Fig.4 The result of PID control

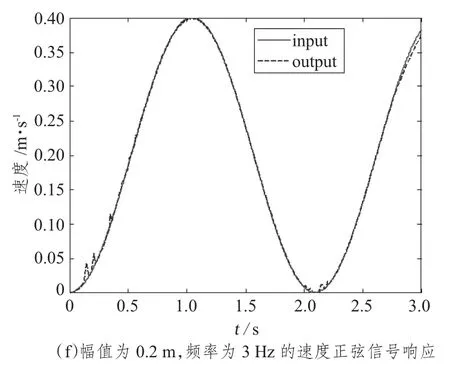
图5 系统模糊-PID控制结果Fig.5 The result of fuzzy PID control

3.3 仿真结果分析

从图4 可以看出: (a)对于位移阶跃信号，系统能较好地进行跟踪，但是一旦产生超调则无法回复到理想的输入值，原因是系统只对液压流量进行控制，无往复控制，即系统对于位移量只有单向控制能力。 (b)对于斜坡位移信号，系统在PID控制下不能很好跟踪，误差量将随时间的增加而增加。 (c)对于速度阶跃信号，系统能在短时间内接近理想输入值，但是随着时间的推移，误差越来越大，其原因是系统的动力源(气腔的压缩空气)所提供的动力在系统的运行过程中逐渐降低，而且采用固定参数式PID控制式系统不能及时获得足够的控制量来弥补系统动力的不足。(d)对于速度斜坡信号，系统同样不能很好跟踪，原因与(c)相同。 (e)和(f)中，系统对于速度正弦信号的跟踪，在低速时较好，在高速时误差比较大。

从图5 中可以看出，系统在模糊-PID控制下对于所选择的输入都能够很好跟踪，其不足之处为:从(c)中可以看出系统对于速度阶跃信号的响应存在较大超调，这跟所选择的控制量有关;从(e)和(f)中可以看出对于速度正弦输入信号，系统在初始段的跟踪能力要好于末端跟踪能力，这主要是由于系统动力不断降低的缘故。

从仿真结果可以看出，模糊-PID控制要优于PID控制，其主要原因有两大方面:其一，系统动力源时变，具体来说动力在系统运行过程中不断降低，而且不是线性变化;其二，系统只进行单程单方向控制，对于位置信号输入，一旦产生超调，系统将无法恢复到理想的输入值。这些也是无源非对称缸气液联控伺服发射系统所独有的特性。鉴于以上分析，传统的PID控制难以满足系统的性能要求，需要采用或结合其他智能控制方法。

4 结 语

在非对称缸气液联控伺服发射系统传递函数的基础上，设计了针对该系统的模糊控制器，并对非对称缸气液联控伺服发射系统进行了PID控制和模糊-PID控制过程仿真，获得多种典型输入信号的跟踪仿真结果。仿真结果显示:模糊-PID控制的效果要优于PID控制，其原因主要是系统的无源及单程控制特性决定的。在设计系统控制器时尤其要注意系统的这2 点特性。本文的研究工作可为后续该类发射系统的控制设计提供参考。

［1］练永庆，王树宗.鱼雷发射装置设计原理［M］.北京:国防工业出版社，2012，4:65 -66.

［2］田兵，吴朝晖，许东风.非对称缸气液联控伺服发射系统动态特性［J］.舰船科学技术，2013，35(10):119 -125.TIAN Bing，WU Zhao-hui，XU Dong-feng.Research on the dynamic characteristic of asymmetric cylinder pneumatic hydraulic combination control servo launching systems［J］.Ship Science and Technology，2013，35(10):119 -125.

［3］曾光齐，胡均安，王东，等.模糊控制理论与工程应用［M］.武汉:华中科技大学出版社，2006.

［4］徐秀芬.气液联控伺服发射系统的控制及其试验研究［D］.哈尔滨:哈尔滨工业大学，2005.

［5］王立新.模糊系统与模糊控制原理教程［M］.北京:清华大学出版社，2003:70 -87.