基于磁流变弹性体变刚度动力吸振器的研究

宋伟志，周 辉，赵艳青，赵海军，姚永玉

(1.洛阳理工学院 机械系，河南 洛阳471000;2.淮阴工学院，江苏 淮安223001)

0 引 言

对于工程结构、建筑桥梁以及机械系统等进行有效的减振十分必要。动力吸振器始于1902年，由Frahm 发明［1］。因为其结构、性能及经济等方面的优势而得到了广泛研究。但传统动力吸振器由于结构参数固定，只有当固有频率等于外界激振频率时，才可对主系统进行有效减振［2］，对于变频激振，其减振性能会大幅降低，严重制约了吸振器的使用范围。

近些年自适应动力吸振器［3－7］由于结构简单，性能稳定，且可以有效拓宽吸振器减振频带而得到快速发展。磁流变弹性体 (Magnetorheological elastomers，MRE)作为一种新型智能材料，兼备磁流变材料及弹性体的性能，同时克服了磁流变液易发生沉降的问题［8］。本文以MRE为弹性元件，设计并研究了基于磁流变弹性体［9］的变刚度动力吸振器。通过理论仿真和实验研究证明，该吸振器通过调节自身刚度，其减振频带可达到5 Hz。当外界激振频率在一定范围发生变化时，吸振器通过追踪外界激振频率，充分发挥其减振性能，对主系统的振动抑制有大幅度提高。

1 基于MRE 变刚度动力吸振器的原理分析

现阶段对于MRE 磁流变效应的分析基于磁偶极子理论［10］。即MRE 中的励磁性颗粒在磁场作用下磁化而彼此产生相互作用力，由于相互作用力的不同导致模量不同。目前MRE的工作模式主要有挤压式和剪切式，鉴于剪切式的磁流变效应较为明显，本文采用剪切式设计结构，基于MRE的吸振器实物如图1所示。高导磁支架、MRE 及吸振器的振子组成闭合磁回路，励磁线圈在电流作用下产生磁场并穿过MRE。

图1 磁流变弹性体动力吸振器Fig.1 DVA based on MRE

MRE 剪切刚度计算如式(1):

式中:k为弹性体刚度;G为弹性体有效剪切模量，其值等于外界不加磁场时的剪切模量G0加上磁场作用下模量变化量ΔG［11］，如式(2)所示;A为弹性体的有效剪切面积;h为弹性体的厚。

根据吸振器固有角频率和本身刚度及质量的关系:

式中:ω为吸振器的固有角频率;k为吸振器弹性元件刚度;m为吸振器振子质量，可知:

根据MRE 刚度与剪切模量的关系及吸振器固有频率与刚度之间的关系易知，可通过改变励磁线圈电流的大小改变穿过MRE的磁场，进而对吸振器的固有频率进行调节，使之等于外界激振频率，充分发挥吸振器的减振性能，实现宽频减振的目的。设吸振器最小刚度(即不加电流时)为kmin，电流最大时，达到磁流变弹性体磁饱和，设其刚度增加为Δk，则吸振器的有效减振频带为，这就是基于磁流变弹性体动力吸振器拓宽减振频带的基本原理。

2 变刚度动力吸振器的仿真研究

可将主系统和吸振器简化为二自由度振动系统，其模型如图2所示。

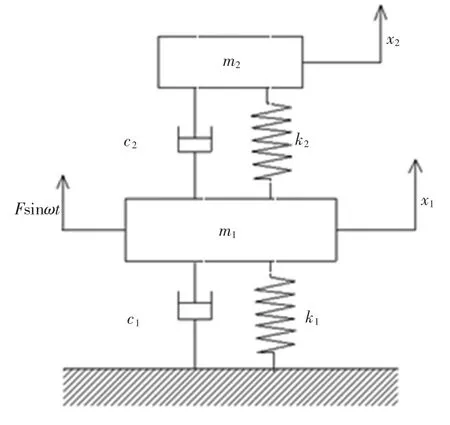
图2 主系统—吸振器模型Fig.2 The model of primary system and DVA

由以上模型建立运动学方程如下:

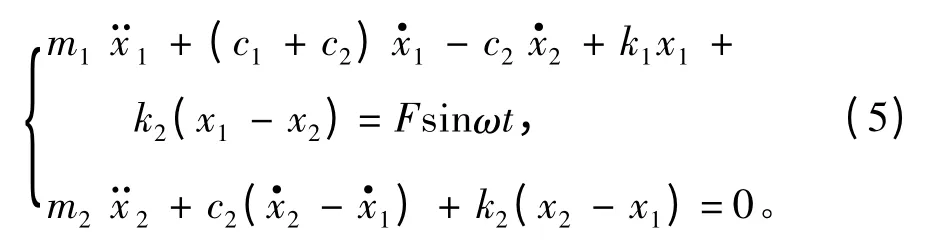
利用上述运动学方程建立模型并进行仿真研究，系统采用结构参数如表1所示。

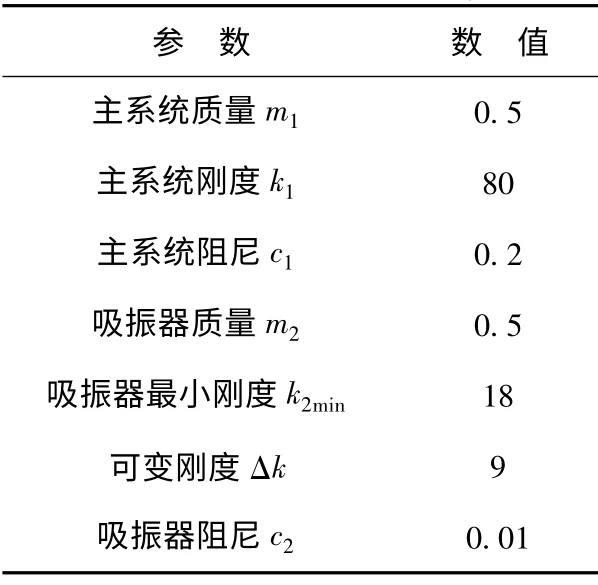
表1 系统结构参数Tab.1 Parameters of the system

利用Matlab/Simulink 模块建立仿真模型，做出主系统的幅频特性曲线，如图3所示。

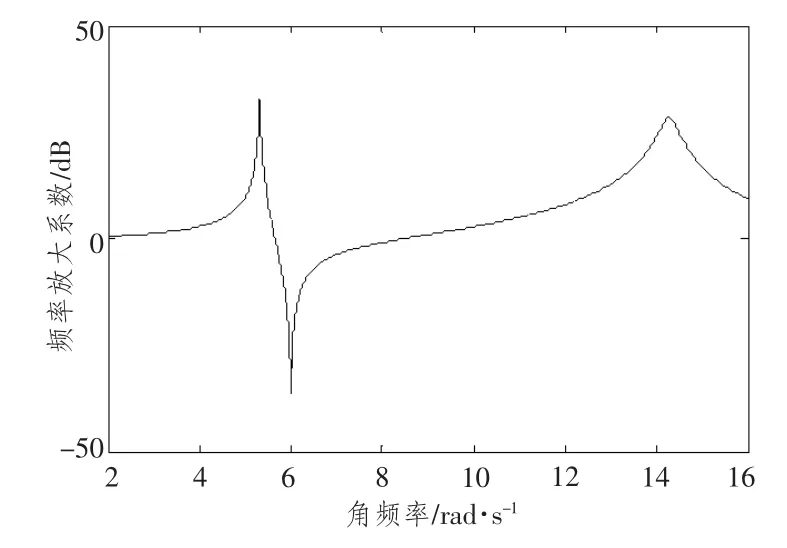
图3 主系统幅频特性曲线Fig.3 Amplitude-versus-frequency curve of primary system

由图3 可知，当外界激振频率等于激振器固有频率时，吸振器减振效果最好，然而激振频率稍有变化，其减振效果大幅降低，甚至引起主系统共振。通过调节刚度，可以改变吸振器固有频率，使吸振器在宽频带上对主系统进行有效减振。图4做出了吸振器在不同刚度下主系统的幅频特性曲线。

由于刚度可连续变化，故在最小、最大刚度下，主系统幅频特性曲线“波谷”形成频带，即吸振器有效减振频带，如图5所示。

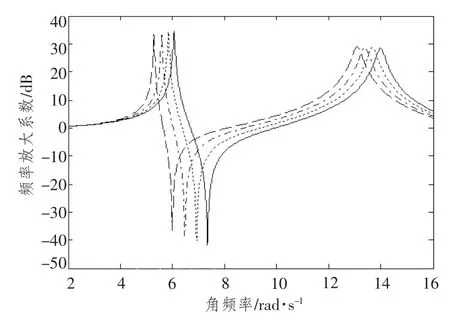
图4 不同刚度下主系统幅频特性曲线Fig.4 Amplitude-versus-frequency curve of primary system in different stiffness

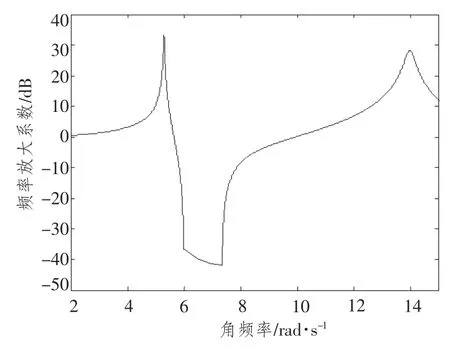
图5 连续调节刚度时主系统幅频特性曲线Fig.5 Amplitude-versus-frequency curve of primary system in continuously adjustable stiffness

为便于观察变刚度吸振器减振效果，图6 给出了主系统的时域响应图。图中，仿真初期吸振器固有频率不等于激振频率，主系统振幅较大，在200 s附近调节吸振器刚度，当其固有频率等于外界激振频率时，主系统振幅明显降低。

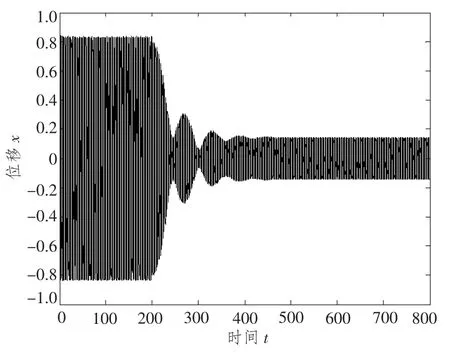
图6 主系统时域振动响应Fig.6 Vibration response of primary system in time

通过上述分析可知，变刚度吸振器可以实现对外界激振频率的追踪，有效拓宽减振频带，充分发挥吸振器的减振性能，这对于工程实际具有重要意义。

3 基于磁流变弹性体变刚度动力吸振器的实验研究

为研究基于MRE 变刚度动力吸振器的宽频减振性能，本部分搭建实验系统，具体如图7所示。工作过程为:激振器接受信号发生器的信号带动主系统振动，传感器采集主系统振动信号经电荷放大器给数据采集仪，对信号进行快速傅里叶分析，数据存储单元对信号存储并得出主系统的幅频特性曲线。实验中做出了电流为0 A，0.5 A，1 A和1.5 A 时主系统的幅频特性曲线，具体如图8所示。由图8可知，在电流从0 增大到2 A的过程中，吸振器固有频率(曲线最低点)由23.48 Hz 增加到28.38 Hz，其减振频带得到有效拓宽。

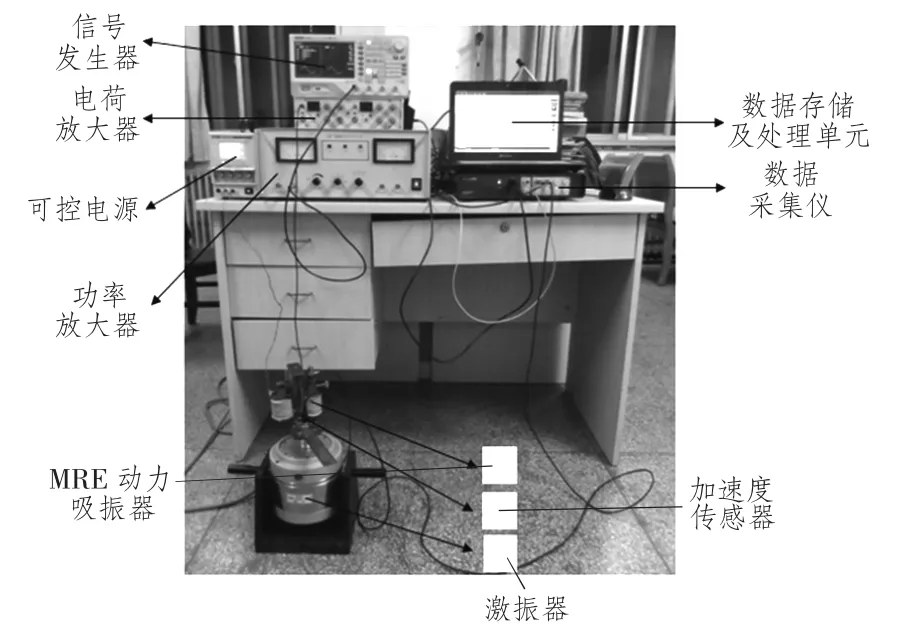
图7 基于MRE的吸振器实验系统Fig.7 DVA experimental system based on MRE

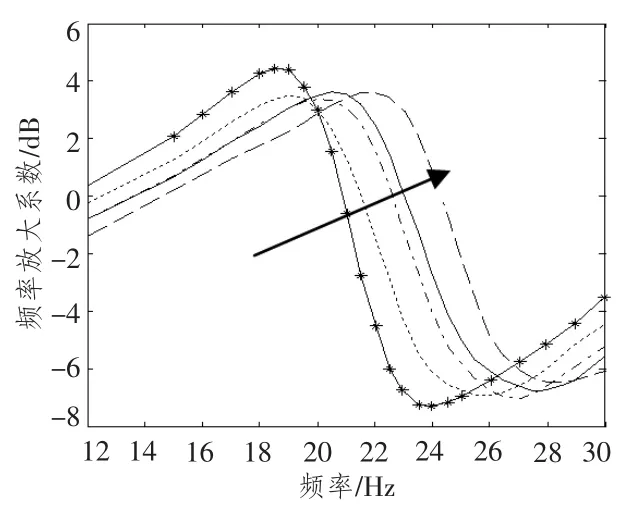
图8 不同电流下主系统幅频特性曲线Fig.8 Amplitude-versus-frequency curve of primary system in different current

基于吸振器的反共振减振原理，由主系统幅频响应可知，曲线最低点处的频率即为吸振器固有频率，结合不同电流下主系统幅频特性曲线可找到吸振器固有频率与电流的关系，具体如表2所示。

表2 吸振器固有频率与电流间关系Tab.2 The relationship between natural frequency of DVA and current

由数据拟合两者关系如图9所示。

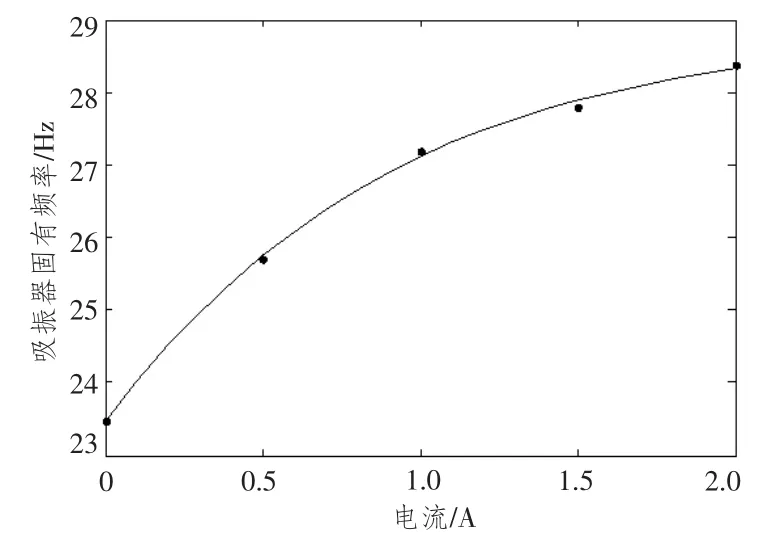
图9 吸振器固有频率与电流关系Fig.9 The relationship between natural frequency of DVA and current

由上述吸振器固有频率与电流的关系曲线，分析主系统在变刚度吸振器作用下的振动情况。使主系统在任意激振频率下振动，当吸振器固有频率不等于激振频率时，利用上述曲线调节电流，以调节吸振器固有频率，实现对外界激振频率的追踪，做出主系统的时域响应图，如图10所示。

图10 主系统时域振动响应Fig.10 Vibration response of primary system in time

由时域图可知，在24 s 之前，吸振器固有频率与外界激振频率不等，主系统振幅为1.83，在24 s 调节电流，以实现吸振器对外界激振频率的追踪，当主系统稳定后，振幅为1.04，幅值降低约43.2%。这说明通过调节吸振器刚度，使其固有频率等于外界激振频率，可有效抑制主系统振动。

4 结 语

文章设计研究了一种基于磁流变弹性体的变刚度动力吸振器。利用磁流变弹性体刚度可控的性能，有效拓宽了吸振器的减振频带。仿真和实验证明，设计的吸振器可通过调节电流来改变刚度，以实现对外界激振频率的追踪，充分发挥了吸振器的减振性能。幅频特性曲线表明，设计的吸振器减振频带达5 Hz;时域图表明，当外界激振频率不等于吸振器固有频率时，可通过调节刚度来改变吸振器固有频率，实现对外界激振频率的追踪，使主系统的振幅降低约43%。这说明对于受变频激励的系统，本文所设计的吸振器具有良好的减振性能。

［1］FRAHM H.1911，“Device for Damping Vibration of Bodies”，US patent:989958.

［2］任明章.动力吸振器及其应用［M］.北京:机械工业出版社，2013.

［3］WILLIAMS K，CHIU G，BERNHARD R.Adaptive-passive absorbers using shape-memory alloys［J］.Journal of Sound and Vibration，2002，249(5):835－848.

［4］GAO Qiang，ZHANG Wei-feng，et al.An adaptive tuned vibration absorber based on variable mass［J］.Noise Control Eng.J，2011，59(5).

［5］DENG H X，GONG X L，WANG L H.Development of an adaptive tuned vibration absorber with magnetorheological elastomer［J］.Smart Materials and Structures，2006，15:111－116.

［6］FRANCHEK M A，RYAN M W.AdaPtive passive vibration controlcJournal of Sound and Vibration，1995，189(5):565－585.

［7］WALSH P L.A variable stiffness vibration absorber for minimization of transient vibration［J］.Journal of Sound and Vibration，1992，158(2):195－211.

［9］龚兴龙，邓华夏，李剑峰，等.磁流变弹性体及其半主动吸振技术［J］.中国科技大学学报，2007，37(10):1192－1203.GONG Xing-long，DENG Hua-xia，LI Jian-feng，et al.Magnetorheological elastomers and corresponding semiactive vibration absorption technology［J］.Journal of University of Science and Technology of China，2007，37(10):1192－1203.

［10］仲维畅.磁偶极子与磁粉探伤［J］.无损检测，1990，12(3):66.ZHONG Wei-chang.Magnetic dipole and magnetic particle inspection［J］.Nondestructive Testing，1990，12(3):66.

［11］DENG Hua-xia，GONG Xing-long.Application of magnetorheological elastomer to vibration absorber ［J］.Communications in Nonlinear Science and Numerical Simulation，2008(13):1938－1947.