Radon_CPF+NLS算法估计性能研究

赵博威，周剑雄，付 强

(国防科学技术大学电子科学与工程学院，长沙 410073)

三阶多项式相位信号在通信、雷达、声纳、生物学、地震学等诸多领域有所应用［1］。例如，复杂运动目标的雷达回波可采用三阶多项式相位信号进行建模［2］，目标的径向速度和加速度可由高阶相位系数估计，且通过参数估计达到辨识目标的目的;生物学领域，可使用三阶多项式相位信号模拟蝙蝠和海豚的声音进行仿生学研究［3］。

许多学者针对三阶多项式相位信号参数估计进行了研究。目前主要的参数估计算法可分为相关法和非相关法两大类，其中相关法参数估计运算量较小，但估计精度在低信噪比时下降严重;相反，非相关法在低信噪比时能得到较高的估计精度，但运算量较大［4］。参数估计的非相关算法主要有最大似然估计方法［5］;参数估计的相关算法主要包括高阶模糊函数(HAF)［6］、三阶多项式相位函数(CPF)［7－8］及其改进算法［9－12］等。相关算法的主要思想是利用高阶非线性变换降低信号相位的维度来实现高阶多项式相位参数估计，但非线性变换降低了多项式相位参数估计的工作起始噪声门限，非线性变换阶数越高，参数估计的工作起始噪声门限就越高。HAF算法采用四阶非线性变换，CPF算法采用二阶非线性变换，所以CPF算法的工作起始噪声门限低于HAP算法，更贴近实际应用。Wang P针对CPF算法只能对单分量信号进行参数估计的缺陷，提出 Radon_CPF算法［13］，将CPF算法推广到多信号参数估计。为进一步提高Radon_CPF算法参数估计的精度，贺思三应用单纯型法对Radon_CPF算法进行改进，提出Radon_CPF+NLS算法。该算法在工作起始信噪比门限之上达到了CRB［14］，但该文献中只给出了等幅信号的参数估计结果，对于影响该算法性能的因素未做研究。针对实际雷达信号处理中多目标情况或邻近散射中心的能量差异和相位参数邻近的情况，该方法是否适用有待考量。本文在贺思三等的工作基础上展开，对影响算法工作的一些因素进行讨论，为该算法应用于实际信号处理提供理论依据。

本文工作分以下小节开展:第1节介绍Radon_CPF+NLS算法的理论基础;第2节介绍算法的估计流程;第3节给出仿真实验，考察数据长度、信号能量、信号相位参数临近等情况对参数估计的影响;第4小节对本文进行总结。

1 Radon_CPF+NLS算法

1.1 Radon_CPF算法

设单分量三阶多项式相位信号的表达式为

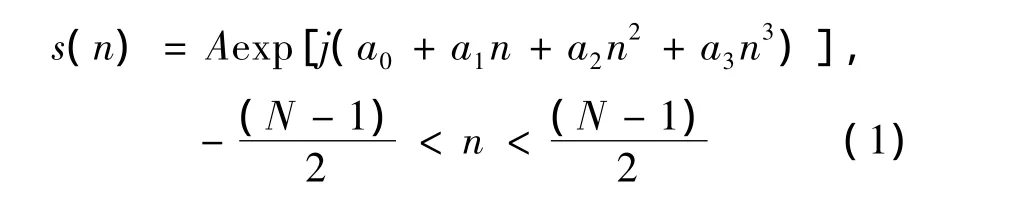
对s(n)做双线性变换，得到

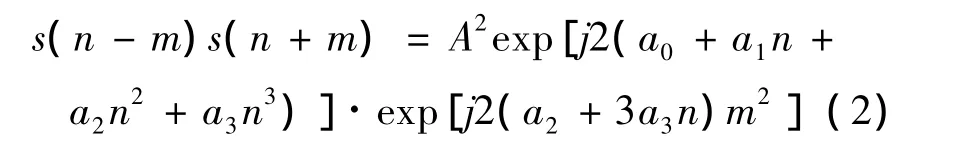
由上式可知:信号s(n－m)s(n+m)关于变量m只有二次项系数 2(a2+3a3n)，基于此，O’SHEA P 提出 CPF算法［7］:

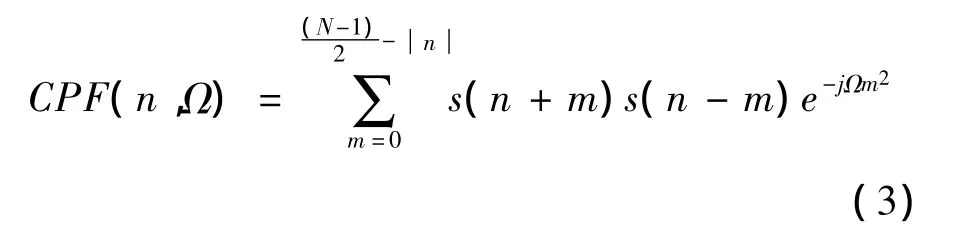
其中:Ω=d2φ(n)/dn2，表示信号的瞬时频率。当Ω=2(a2+3a3n)时，CPF函数会在(n，Ω)域形成一条直线，从而实现对参数估计的降阶处理。对于单分量，可选取2个不同时刻的Ω值，解方程组得到a2，a3的值。但对多信号进行CPF运算后，发现在(n，Ω)域存在多条直线，该方法不再适用。为将CPF算法应用到多信号参数估计，Wang P将Radon变换与CPF函数结合，提出Radon_CPF算法，实现了多分量信号参数估计［13］。

Radon函数定义如下:

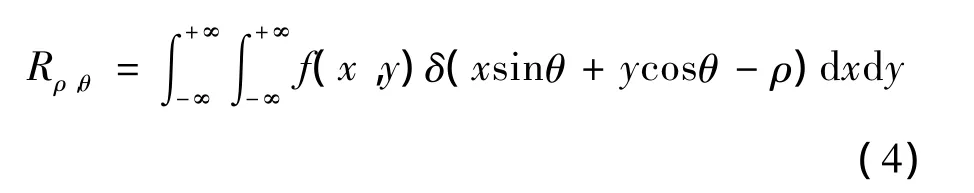
其中:－∞ ＜ρ＜ +∞，0＜θ＜π。

Radon_CPF函数定义如下:

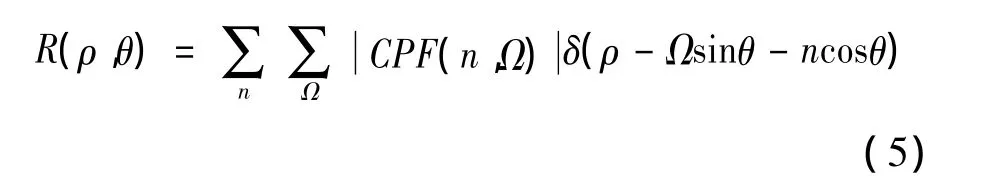
其中的δ(·)表示狄拉克函数。

假设利用Radon变换对CPF变换后的(n，Ω)域进行直线参数提取，得到参数(ρ0，θ0)，则对应直线的斜率和截距分别为－cotθ0和 ρ0/cosθ0。根据几何关系得到待估计信号相位的2次项系数和3次项系数:

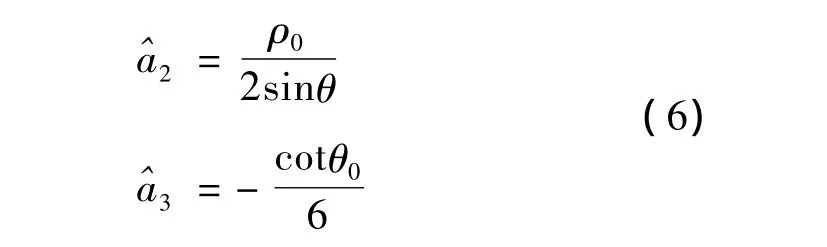
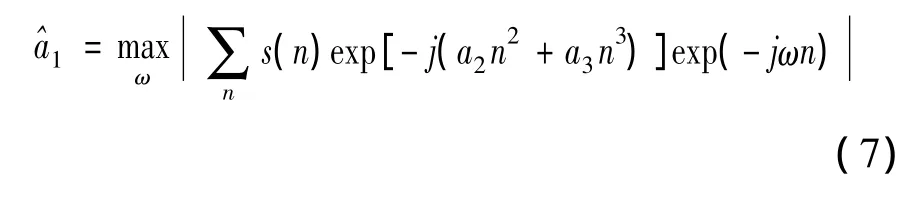
实际计算过程中，由于量化误差、CPF自身估计性能限制以及噪声的影响，估计精度不高，要想得到较高精度的估计结果，需要对粗估计结果进行精估计以得到更精确的参数。

1.2 Radon_CPF结果的精估计算法

假设在白噪声条件下，信号x(n)由K个P阶多项式相位信号组成:

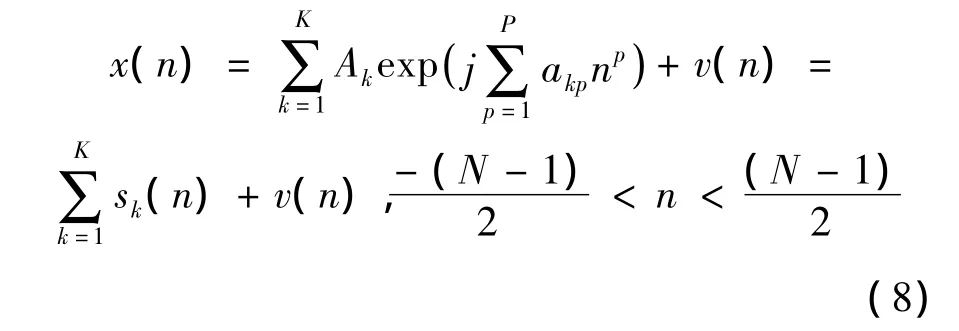
其中:akp表示第k个分量的相位多项式第p阶系数;Ak表示第k个分量的幅度系数;v(n)表示均值为0、方差为σ2的高斯白噪声，且不同时刻噪声相互独立。定义:

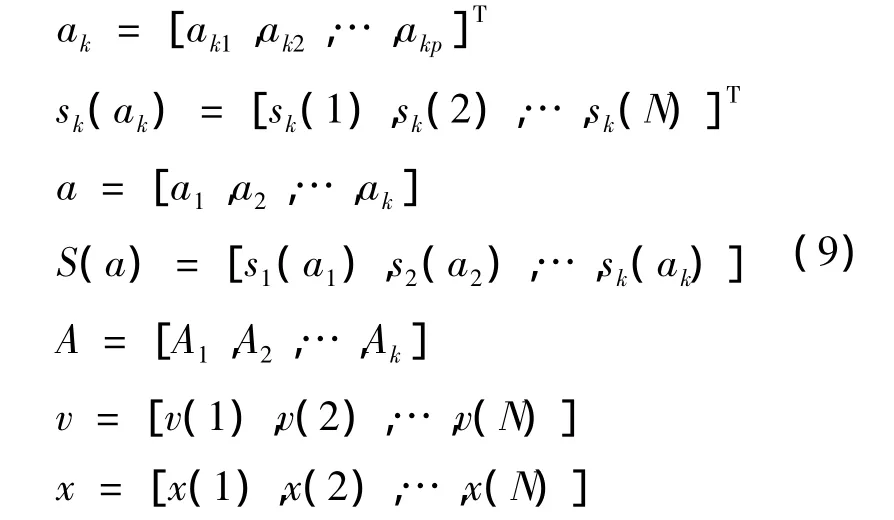
将式(8)改写为矩阵形式

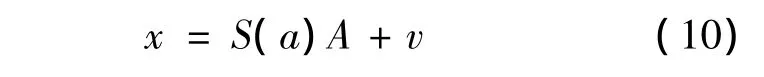
待估计参数a的最大似然估计结果表达式为［15］

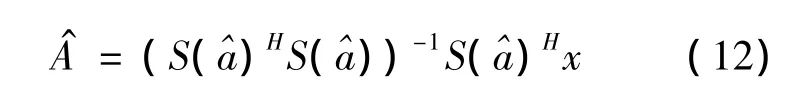
上式表明多项式相位参数估计问题是一个多参数的非线性优化问题［14］。在包含噪声或多分量的情况下目标函数在参数空间的形式极为复杂，现有成熟算法只能保证其收敛到局部极值，且优化结果对初值的设定非常敏感。Pham D S对现有的主要优化算法进行了比对，验证了单纯型法有较好的优化性能［15］。本文采取单纯型法进行优化。

2 算法流程

对于多分量信号参数估计，利用Clean思想对单个分量进行依次估计并优化，得到所有估计值后再对多分量估计结果进行联合优化。设K个信号的和为y(n)，具体流程如下:

1)令k=1，x(n)=y(n);

2)根据式(3)对信号x(n)进行CPF变换;

3)根据式(5)对CPF结果进行Radon变换，利用式(6)得到参数，利用式(7)得到参数;

5)令x(n)=x(n)－Akexp(j(ak1n+ak2n2+ak3n3))，k=k+1。重复步骤2)～4)，直至估计信号数目达到设定信号分量的上限K;

6)将(a1，a2，…，aK)作为式(11)所示目标函数的初始值，进行联合估计，得到相位估计参数a，代入式(12)得到幅度估计结果A。

3 实验验证

3.1 数据长度对估计性能的影响

设置数据长度N=257，信号幅度A=1，相位参数(a1，a2，a3)=(π/8，0.005，1e－5)。在原始信号中加入高斯白噪声至一定信噪比水平，进行500次蒙特卡洛实验，验证 Radon_CPF算法和Radon_CPF+NLS算法的估计性能。由结果可以看出:Radon_CPF算法和Radon_CPF+NLS算法的起始工作信噪比门限都在－4dB，但信噪比大于－4 dB时，后者的参数估计更加精确，参数估计方差接近 CRB［15］。

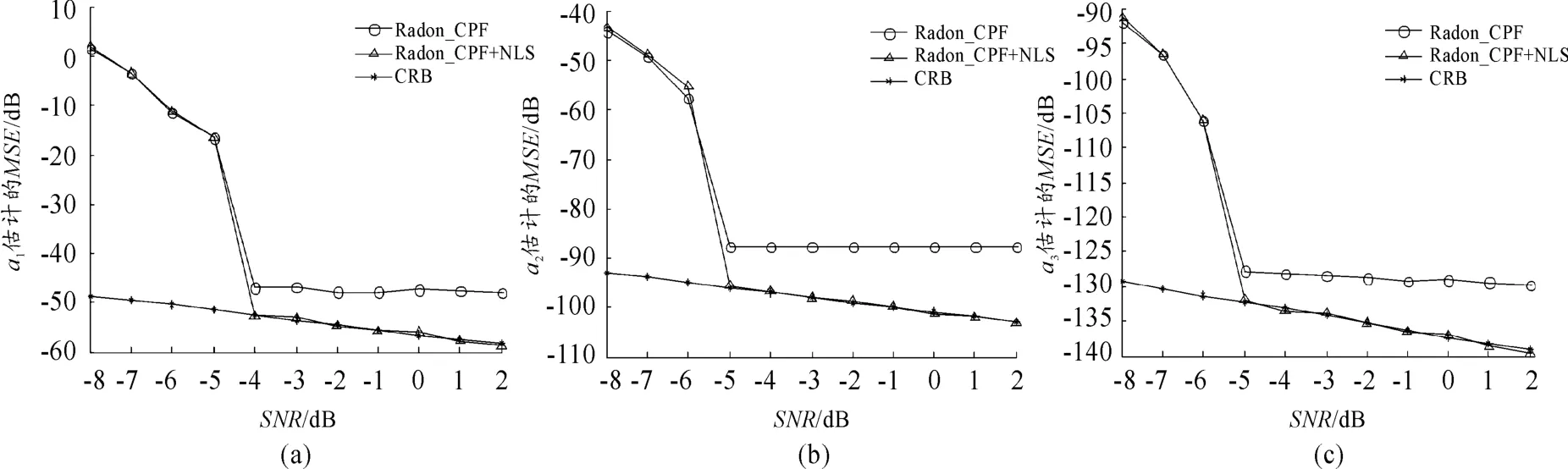
图1 单分量信号参数估计结果

参数设置不变，对信号加入高斯白噪声至SNR=－2 dB，改变数据长度，研究数据长度对参数估计性能的影响，实验结果如图2所示。从实验结果可以看出:相同信噪比情况下，数据长度越长，参数估计的精度越高，但同时运算量迅速增大，运算量为O(N2)。因此，实际应用时应权衡参数估计精度与运算速度的要求，选择合适的数据长度进行参数估计。

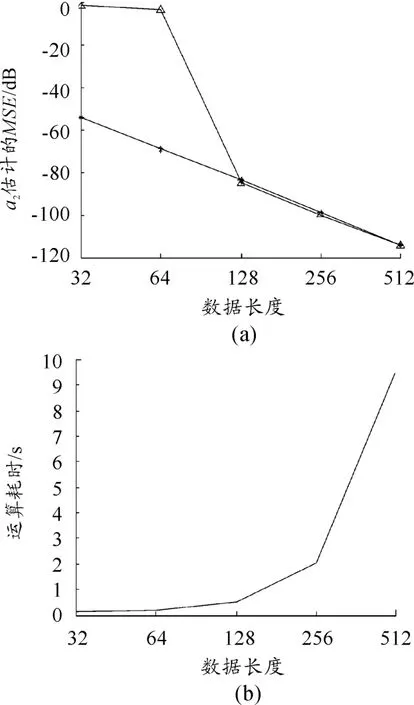
图2 数据长度对估计精度和运算时间的影响

3.2 多分量信号能量对估计性能的影响

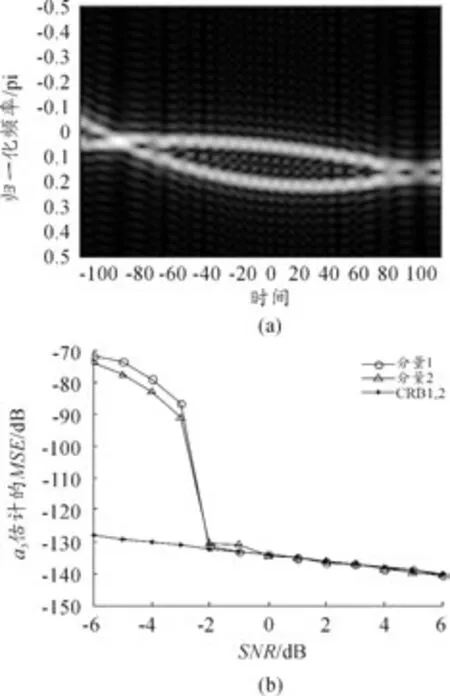
图3 两等幅三阶多项式相位信号的参数估计性能分析

改变两分量信号幅度A1=1，A2=2，其他实验参数不变，考察信号能量对参数估计性能的影响，实验结果见图4。由结果可以看出:两信号分量工作信噪比起始门限相差6 dB;当达到算法工作的起始信噪比门限后，同一信噪比条件下两信号分量的估计方差也相差6 dB。理论分析结果表明:在均值为0、方差为σ2的高斯白噪声条件下，两分量信号参数估计方差差距的理论值为dB，实验结果与理论值相同。实验结果表明:多分量情况下，本文算法更适合估计能量较大的信号，若信号能量相差过大，小能量信号估计性能较差。

3.3 多分量信号参数临近对估计性能的影响

设置信号参数 A1=A2，a12=a22，a13=a23，a11和a21间的差距由0个傅里叶分辨单元逐渐增大至19个傅里叶分辨单元，每种情况下进行100次蒙塔卡洛实验，加入高斯白噪声至SNR=0 dB，参数估计误差曲线如图5所示。可以发现:在信号2次项系数和3次项系数相同的情况下，信号1次项分量差距小于7个傅里叶分辨单元时，信号参数估计性能较差;当两信号1次项分量差距在7个傅里叶分辨单元以上时，参数估计方差达到了CRB。实验结果说明:当两信号频谱过于靠近时，算法估计性能下降，估计误差增大;只有信号频谱分开一定程度时，算法估计才能得到较为精确的估计结果。

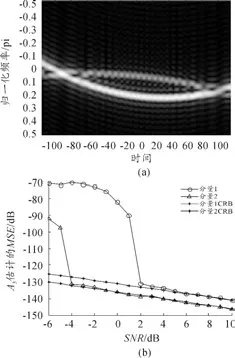
图4 两不等幅三阶多项式相位信号的参数估计性能分析

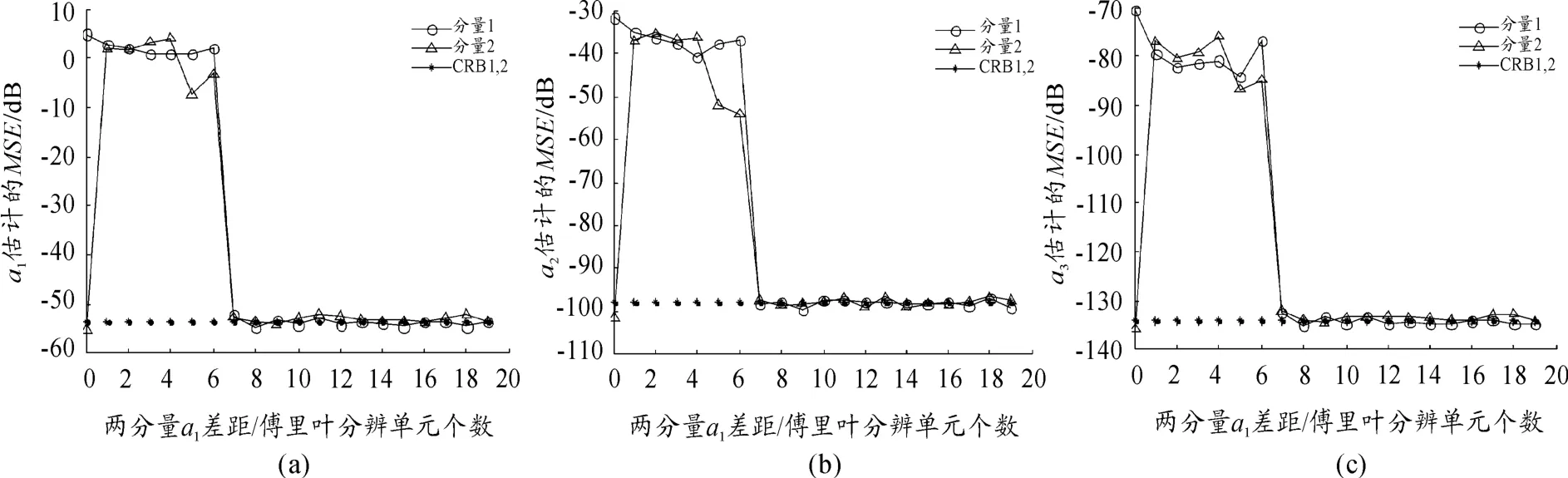
图5 a1分量临近对参数估计性能的影响

4 结束语

三阶多项式相位信号应用广泛，但参数估计较为复杂，估计方法优劣各异。本文针对三阶多项式相位信号参数估计算法Radon_CPF+NLS展开研究，分别讨论了数据长度、多分量时信号能量、多分量相位参数临近等情况对信号相位参数估计性能的影响，通过实验仿真指出了该方法在信号处理应用中的适用范围，为算法的工程应用提供了理论基础，对算法的实际应用具有参考价值。

［1］MCKILLIAN R G，CLARKSON I V，QUINN B G，et al.The Asymptotic Properties of Polynomial Phase Estimation by Least Squares Phase Unwrapping［C］//2011 IEEE International Conference on，Acoustics，Speech and Signal Processing(ICASSP).Italy:［s.n.］，2011:3592－3595.

［2］LEVANON N，MOZESON E.Radar Signals［M］.USA:Wiley，2004.

［3］THOMAS J A，MOSS C F，VATER，et al.Echolocation in bat and dolphins［J］.The Journal of the Acoustical Society of America，2005，118:2755，2005.

［4］ZHENG J，SU T，LIU Q H，et al.Fast parameter estimation algorithm for cubic phase signal based on quantifying effects of Doppler frequency shift［J］.Progress In Electromagnetics Research，2013，142:57－74.

［5］ABOTZOGLOU T.Fast maximum likelihood joint estimation of frequency and frequency rate［J］.IEEE Trans Aerosp Electron Syst，1986，52:385－393.

［6］PELEG S，PORAT B.Linear FM signal parameter estimation from discrete-time observations［J］.Aerospace and Electronic Systems，IEEE Transactions on，1991，27(4):607－616.

［7］O’SHEA P.A new technique for instantaneous frequency rate estimation［J］.Signal Processing Letters，2002，9(8):251－252.

［8］O’SHEA P.A fast algorithm for estimating the parameters of a quadratic FM signal［J］.Signal Processing，IEEE Transactions on，2004，52(2):385－393.

［9］WANG Y，JIANG Y C.ISAR imaging of a ship target using product high order matched-phase transform［J］.IEEE Geosci.Remote Sens.Lett.，2009，6(4):658－661.

［10］WANG Y.Inverse synthetic aperture radar imaging of manoeuvring target based on range instantaneous Doppler and range instantaneous Chirp-rate algorithms［J］.IET Radar，Sonar and Navigation，2012，6(9):921－928.

［11］O’SHEA P.A new class of multilinear functions for polynomial phase signal analysis［J］.IEEE Trans，Signal Process，2001，57:2096－2109.

［12］TANG P，YUAN B，LIN Q，et al.An Efficient algorithm for estimating the parameters of multicomponent cubic phase signals［J］.ICCSEE－13，2013.

［13］WANG P，YANG J，XIONG J，et al.Multicomponent Quadratic FM Signals Analysis Using Radon-CPF Transform［C］//Radar，2006.CIE’06.International Conference on.［S.l.］:IEEE，2006:1－4.

［14］贺思三，赵会宁，刘铮，等.三阶多项式相位信号参数估计［J］.信号处理，2010，26(9):1366－1370.

［15］PHAM D S，ZOUBIR A M.Analysis of multicomponent polynomial phase signals［J］.Signal Processing，IEEE Transactions on，2007，55(1):56－65.