基于云理论的复杂系统MTTR验证方法研究

韩朝帅 曹军海 王玉泉 陈守华

装甲兵工程学院，北京100072

平均修复时间(Mean time to repair ，MTTR)［1］是指在规定的条件、维修级别和环境下，产品修复一次需要的平均时间，是最能体现产品维修性水平的一种维修性参数。随着新装备的综合集成化水平日益提高，装备系统中机械部件、电子设备和光学元件多元混联并行的模式使装备的复杂程度越来越高，系统MTTR 的不确定性随之大大提高。

常用的MTTR 验证方法是采用传统的统计学方法对试验生成的限量样本进行处理分析，近来有专家提出依据相似学原理对MTTR 进行分组验证［2］、采用Bayes 分析法解决小子样问题等［3］，这些方法适用于解决简单系统问题，不能精确反映复杂系统MTTR 的不确定性。云的出现很好的解决了这个问题。

1 云理论概念

“云”这个概念是由李德毅院士［4］于1995年首次系统的提出，用于解决复杂系统中的不确定性问题，为实现定性和定量指标间的转换打下了坚实基础。随着云理论的不断创新发展，云模型已经被广泛应用到各个领域的预测、综合评价、数据挖掘、算法改进、知识表示和模式识别等重要研究项目中，且随系统复杂程度的不断提高，云理论的推广和应用将是各学科研究发展不可逆转的趋势。

云模型是用数字域来表示定性概念与其数值度量之间的不确定性关系的转换模型。设X 为一个定量数值论域，x 为定性概念U 的一个随机定量值，x ∈X，则x 对U 的确定度μi(x)称为x 对U 的隶属度，μi(x)∈［0，1］。隶属度μ(x)在论域X 上的分布称为定性概念U 的云，x 称为云中的一个云滴。

期望Ex，熵En 和超熵He 是云的3个数字特征，分别代表定性概念在论域中的中心极限值、模糊程度和模糊程度的随机性，在云形中反映为云形的最高点，云形的“跨度”和云形的“厚度”。这3个数字特征将定性概念的模糊性和随机性巧妙结合起来，实现了定性概念和定量度量的相互映射。图1为正态云模型及其数字特征。

图1 正态云模型及其数字特征

云模型一般分为正态云、半正态云、梯形云和半梯形云，其生产算法称为云发生器。云变换的一般数学表达式［5］为:

其中，ai是幅度系数;n 为云变换后定性概念的个数;EX1= EX2时，云模型为正态云或半正态云;EX1＜EX2时，云模型为梯形云或半梯形云。

按功能将云发生器分为正向云发生器和逆向云发生器。图2 和3 分别是正向云发生器和逆向云发生器的原理图。由图可知，正向云发生器为输入3个特征值和云滴数n，输出任意云滴x 在论域X 中的坐标和其隶属度μi(x);逆向云发生器是正向云发生器的反向过程，输入某一分布的云滴坐标和隶属度，输出云的3个特征值。其中，x 条件云发生器和y 条件云发生器是2 种最基础的单条件规则云发生器。x 条件云发生器是将x = x0代入3个特征值已知的云发生器中，得到该云滴的隶属度μ(x0);y条件云发生器是将y = y0代入云发生器中得到该隶属度对应的云滴值。

图2 一维正向云发生器

图3 一维逆向云发生器

2 复杂系统MTTR 分解模型

根据复杂系统结构高度模块化的特点，将系统分解到总成级，各总成之间相互独立，寿命分布一般服从指数分布，如图4 所示。

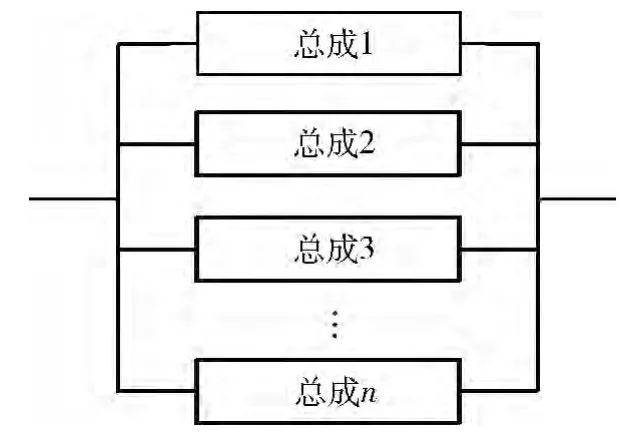
图4 复杂系统一般分解模型

根据图4 系统结构，对系统进行故障树分析(FTA)，其FTA 约定为:

1)不考虑外力强制破坏造成的故障;

2)系统各组成单元发生故障相互独立;

3)系统和其组成单元只考虑发生或不发生故障2 种状态;

4)寿命分布均服从指数分布。

假设系统各组成单元的故障分别为{1，2，3，…，j，…，n}(n个单元)，则系统所有故障组合集合为:U = {(1)，(2)，(3)，…，(n)，…(i，j)，…，(i，j，k)，(1，2，3，…，n)}

则系统MTTR 的计算公式［6］为

其中，w 为系统所有故障组合集合;W = {(1)，(2)，(3)，…，(m)，…，(i，j)，…，(i，j，k)，…，(1，2，3，…，m)}中的一个元素;Nw表示针对故障组合w的虚拟维修工作;E(T| Nw)指进行Nw所需的维修时间;P(Nw)指Nw的发生概率。

而

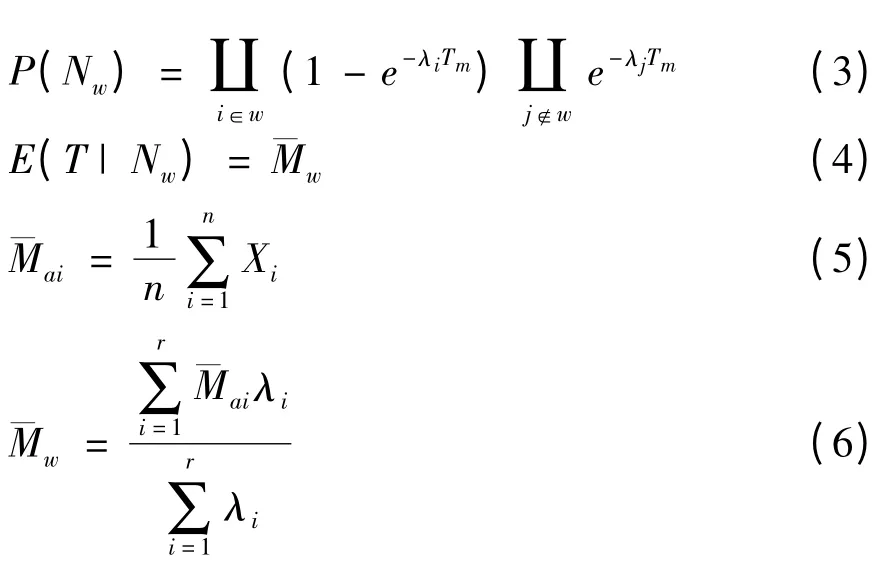
其中，r 为故障组合w 中的故障总成数;Tm为系统工作时间;λi，λj分别为单元i 和j 的故障率;为总成i 的维修时间;X 为试验采集维修时间数据样本X = {X1，X2，…，Xn}，维修时间一般服从对数正态分布。

所以，

一般λiTm很小，近似认为eλiTm≈1 + λiTm，则

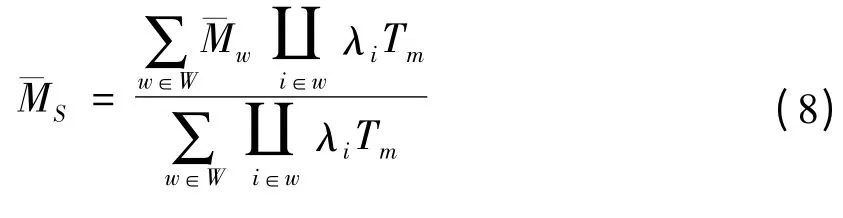
其中，Tm为系统预计工作时间;λi，λj分别为单元i和j 的故障率;为故障组合w 的维修时间，由各故障总成的维修时间加权得到。

3 复杂系统MTTR 云模型

3.1 MTTR 云化流程

3.1.1 MTTR 定性概念论域

相对于旧装备，新装备采用的技术手段革新率一般不能超过25%［7］。从不同型号的装备中选取同一(子)系统的MTTR 数据，将其作为历史数据，通过云变换算法(1)进行处理，得到能代表该(子)系统MTTR 水平的定性概念Ai(Ex1，Ex2，Eni，Hei)，构建出MTTR 定性概念论域X。

3.1.2 MTTR 云模型

同一型号装备系统中的(子)系统MTTR 云模型一般为正态模型［8］。通过试验得到新装备中(子)系统i 的MTTR 样本，将其作为一个云滴，利用逆向正态云发生器得到(子)系统i 的正态云Ui(Exi，Eni，Hei)。

3.1.3 计算隶属度

将第3.1.2 中得到的各(子)系统MTTR 云模型的期望值作为云滴，输入x 条件云发生器求出对各概念的隶属度，通过隶属度最大值法［9］得到各(子)系统的对应概念，进而得到各(子)系统的MTTR 评估结果。图5 为MTTR 云化过程示意图。

3.2 总成级MTTR 云模型

根据复杂系统MTTR 分解模型及MTTR 云化流程可知，总成级MTTR 云模型为:

X 为试验采集维修时间数据样本，X = {X1，X2，…，Xn}，维修时间一般服从对数正态分布。

3.3 系统级MTTR 云模型

根据复杂系统MTTR 分解模型及MTTR 云化流程可知，系统级MTTR 云模型为:

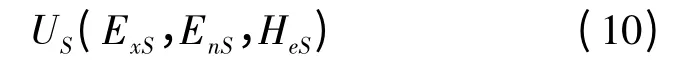
图5 MTTR 云化过程示意图

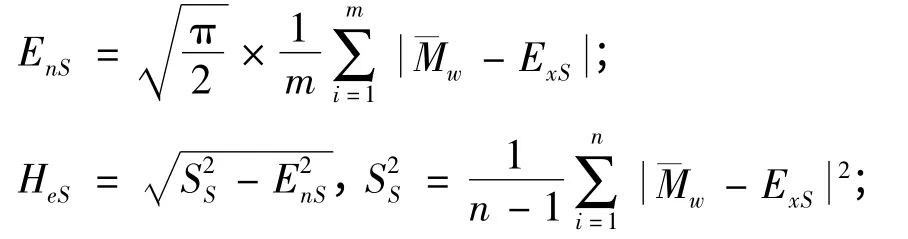
Tm为系统预计工作时间;λi，λj分别为单元i 和j 的故障率;m 为故障组合w 的数量;为故障组合w的维修时间，

综合系统与各总成的最大隶属度及MTTR 期望值，填写MTTR 验证登记表，进而提出设计修改建议。表1 为复杂系统MTTR 验证登记表。

表1 复杂系统MTTR 验证登记表

4 示例分析

M 型车辆传动装置一般工作时间T =2h，其主要由主离合器、前传动、变速箱、制动器和侧减速器组成。对该传动装置各总成进行演示验证试验，表2 为试验得到的各总成维修时间样本。

4.1 总成级MTTR 云模型

利用MTTR 云模型对各总成级进行MTTR 验证，以变速箱为例。首先，选取5 种其它型号的车辆，随机抽取500 组变速箱MTTR 数据进行云变换算法处理，得到4个变速箱MTTR 的定性概念:“优”A31(6.8，0.4121，0.01423)，“良”A32(7.5，0.4520，0.01542)，“中”A33(8.4，0.4520，0.01421)，“差”A34(9.3，0.4121，0.01762)。云形如图6 所示，A31，A32，A33和A34均为正态云模型，这4个概念对变速箱MTTR 进行了定性描述。

其次，由式(9)得到变速箱MTTR 云模型:U3(7.98，0.5032，0.0245)。最后，将期望值7. 98输入x 条件云发生器，求得该变速箱在各个论域的隶属度为(0.45，0.84，0.89，0.32)，故其最大隶属度为A33= 0.89 。图7 为该变速箱MTTR 云图。

表2 传动系统各总成维修时间样本

图6 变速箱MTTR 定性概念模型

图7 变速箱MTTR 云图

同理，求得其它4个总成的MTTR 云模型，如表3 所示。

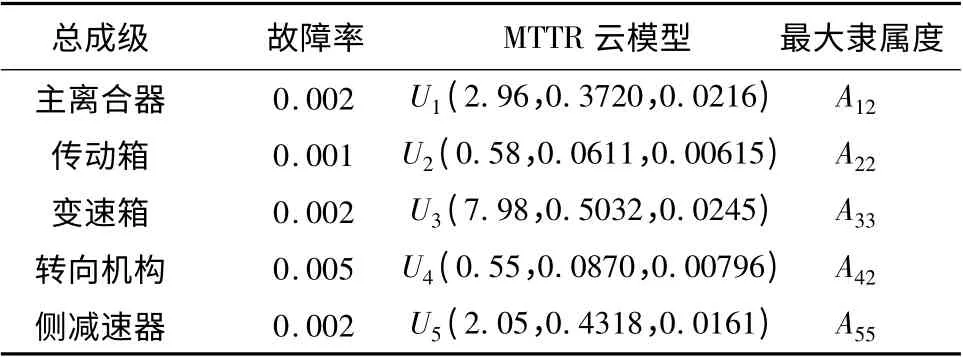
表3 M 型车辆传动系统总成级云模型登记表

4.2 系统级MTTR 云模型

按3.1.1 得出M 型车辆传动系统MTTR 的定性概 念 为: “ 优 ”A1(2.0，0.4212，0.01552)，“良”A2(2.5，0.4321，0.01642)， “中”A3(3.0，0.4622，0.01421)，“差”A4(3.5，0.4341，0.01672)。云形如图8 所示。

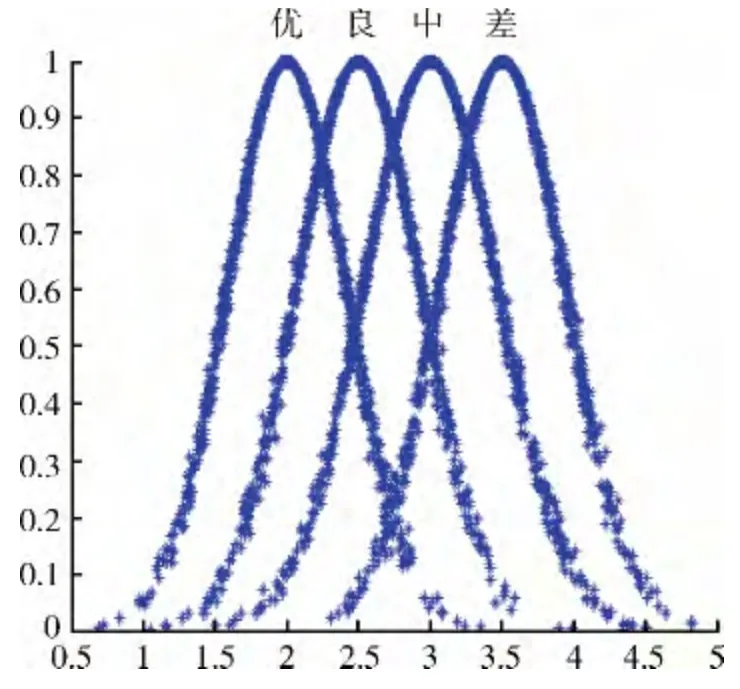
图8 传动系统MTTR 定性概念模型

将表2 中各总成MTTR 云模型的期望值代入式(10)，得到系统MTTR 云模型:U3(2.44，0.4431，0.0145)将期望值7.98 输入x 条件云发生器，求得该变速箱在各个论域的隶属度为(0.55，0.88，0.39，0.22)，故其最大隶属度为A2= 0.88 。图9 为该传动系统MTTR 云图。

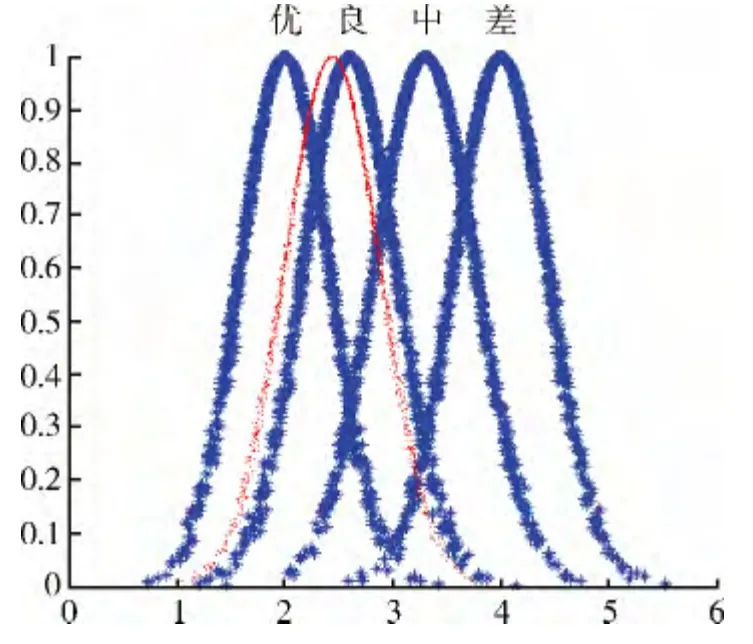
图9 传动系统MTTR 云图

结合表3 得到传动系统MTTR 验证表，如表4所示。

4.3 对比分析

由表4 可知，该传动系统MTTR 试验值为2.44h，总体性能为“良”，总成级部件中主离合器、传动箱和转向机构维修性能均为“良”，变速箱维修性能为“中”，侧减速器维修性能为“差”。通过查询资料，该传动系统的MTTR 合同值为2.6h，故验证结果为:该传动系统MTTR 基本满足要求，但变速箱维修性能较低，侧减速器维修性能很差，可适当考虑对侧减速器结构设计进行改进。

表4 传动系统MTTR 验证登记表

采用统计学方法对表2 中数据进行分析，得出结果是该传动系统的MTTR 为2.44h。将之与云模型验证结果进行对比得出:通过云模型得到的MTTR 验证结果不仅能精确反映系统和各总成的MTTR 真实水平，更能准确详细地向设计者或研制者提供有据的维修性更改意见。

5 结语

针对复杂系统MTTR 的不确定性特点，本文提出基于云理论的复杂系统MTTR 验证方法。该方法可以得到精准度较高的MTTR 验证结果，以期为维修性工程理论和实践研究提供一定的参考价值。

［1］甘茂治，等. 维修性设计与验证［M］. 国防工业出版社，1995. (Gan Maozhi，et al. Maintainability Design and Validation［M］. National Defense Industry Press，1995.)

［2］高伏，郝建平，王松山. 相似学原理在MTTR 分组验证中的应用［J］. 计算机工程，2011，37(5):247-248.(Gao Fu，Hao Jianping，Wang Songshan. Application of Similarity Theory in Grouping Verification of MTTR［J］.Computer Engineering，2011，37 (5):247-248.

［3］李建伟，陈先有，赵小全，王栋. 基于Bayes 理论的小子样维修性验证方法研究［J］. 直升机技术，2012，(1):24-26. (Li Jianwei，Chen Xianyou，Zhao Xiaoquan，Wang Dong. Research on small sample maintainability method based on bayes theory［J］. Helicopter Technology，2012，(1):24-26.)

［4］李德毅，孟海军，史雪梅. 隶属云和隶属云发生器［J］. 计算 机研 究 与 发 展，1995，32(6):16-18. (Li Deyi，Meng Haijun，Shi Xuemei. Membership cloud and cloud generator［J］. Journal of Computer R＆D，1995，32 (6):16-18.)

［5］蒋建兵，梁家荣，江伟，顾志鹏.梯形云模型在概念划分及提升中的应用［J］.计算机工程与设计，2008，29(5):1235-1239. (Jiang Jianbing，Liang Jiarong，Jiang Wei，Gu Zhipeng. Application of trapezoidalcloud model in conception division and conception exaltation［J］.Computer Engineering and Design，2008，29(5):1235-1239.)

［6］于永利，朱小冬，郝建平，张柳.系统维修性建模理论与方法［M］.国防工业出版社，2007.(Yu Yongli，Zhu Xiaodong，Hao Jianping，Zhang Liu. System Maintainability Modeling Theory and Method［M］. National Defense Industry Press，2007.)

［7］单志伟，等. 装备综合保障工程［M］. 国防工业出版社，2007. (Shan Zhiwei，et al. Equipment Integrated Support Engineering ［M］. National Defense Industry Press，2007.)

［8］叶琼，李绍稳，张友华，等.云模型及应用综述［J］.计算机工程与设计，2011，32(12):4198-4201. (Ye Qiong，Li Shaowen，Zhang Youhua，et al. Cloud model and application review［J］. Computer Engineering and Design，2011，32(12):4198-4201.)

［9］蒋建兵，梁家荣，江伟，顾志鹏.基于云理论的学习评价模型研究［J］. 计算机与现代化，2008，(3):17-19. (Jiang Jianbing，Liang Jiarong，Jiang Wei，Gu Zhipeng. Research on Learning Evaluation Model Based on Cloud Theory［J］. Computer and Modernization，2008，(3):17-19.)