基于滑模观测器的充液航天器姿态控制*
2015-12-05史星宇齐瑞云
史星宇 齐瑞云
南京航空航天大学自动化学院,南京210016
目前常用的航天器燃料要求体积小,重量轻,但需要释放很多热量,目的是减轻航天器的质量,延长在轨时间。由于液体燃料释放的能量多,又能产生很大的推力,而且液体燃料比较容易控制,燃烧时间较长,因此,目前的航天器大都采用液体燃料。在人类航天事业不断发展的同时,航天器携带的液体燃料和液态冷却剂也逐渐增加。根据相关文献,液体燃料总质量可达到运载火箭总质量的90%以上、卫星或探测器总质量的50%以上[1]。液体燃料虽然在动力提供上有很多的优点,但不可避免的晃动问题也受到了广泛关注。一旦液体燃料的晃动对航天器产生的干扰力、干扰力矩及冲击压力,超过了控制系统可调节或结构所能承受的上限,将造成控制系统不稳定或结构的破坏[2]。如1969年“Apollo-11”月球探测器首次于月球表面着陆的最后几秒中,残余液体燃料的晃动引起了预期外的探测器抖动,从而影响了落点精确[3];1998年,美国国家航空航天局发射的NEAR 探测器在驶向“爱神433”小行星途中航天器姿态与液体燃料晃动之间的耦合导致一个推进系统失效,导致任务延迟了13个月[4]。
目前,国内外针对晃动问题的主动控制策略主要有:文献[5 -6]使用极点配置自校正控制策略实现了姿态角的镇定及跟踪;文献[7]利用文献[13]中分层滑模的控制方法设计了姿态控制器,提供了欠驱动的控制方法;文献[8 -11]基于Lyapunov 稳定性原理设计了非线性反馈控制器;文献[12]针对充液航天器应用神经网络动态逆控制进行姿态控制;文献[17 -18]考虑液体晃动参数的不确定性,提出了一种参数自适应的非线性反馈控制方法。这些文献大多采用单摆摆角等效液体晃动角的方法,并且假设液体晃动角和角速度可测。但实际上,小幅晃动的液体晃动角和角速度很难测量得到,因此有必要考虑相应的解决方法观测液体晃动角的状态。
本文针对液体晃动角不可测量的情况设计了状态观测器。目的是通过观测器得到液体晃动估计角,并使其在一定的误差范围内逼近真实值。研究时将使用已有的控制器简化非线性充液航天器数学模型,并在此基础上设计滑模观测器,得出晃动估计角,最后将其带入原控制器中,验证估计角对航天器姿态的稳定效果。仿真实例验证了该滑模观测器适用于充液航天器系统。
1 航天器数学模型
本文研究的是一类在零重力条件下、有恒定推力且有固定轴向加速度的充液航天器系统,其液体燃料晃动效果由单摆摆动近似表示,液体燃料晃动角等效为单摆摆角。充液航天器模型如图1 所示。
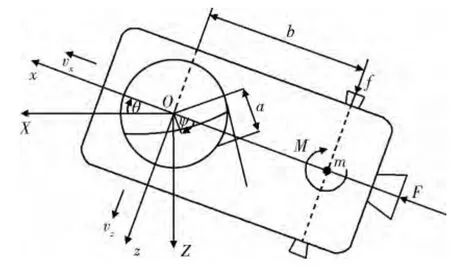
图1 充液航天器示意图
x 轴和z 轴为惯性坐标系。充液航天器存在恒定推力F,沿机体轴有速度vx;受控制输入f 和M影响,有垂直于机体轴的横向速度vz,其中f 为横向推力、M 为作用于质心的转动力矩;充液航天器整体质量为m,贮箱内液体燃料固定质量为mf;充液航天器相对贮箱中心转动惯量为I,If为其相对贮箱中心的转动惯量;航天器质心到贮箱中心距离为b,a 为单摆摆长;航天器姿态角由θ 表示,液体晃动角等效为单摆摆角φ。充液航天器动力学方程由文献[8]推导得出:
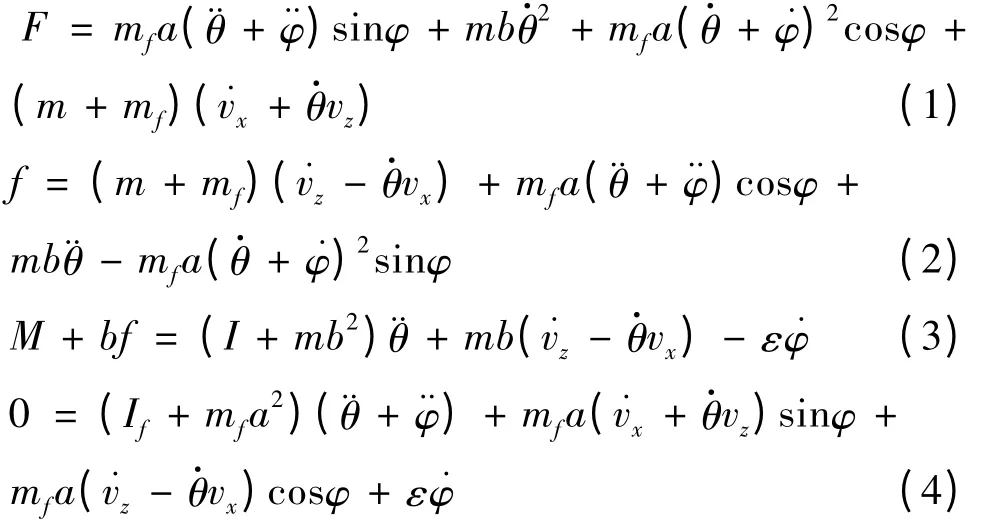
式(4)中,ε 为能量耗散系数。由于全阶的系统非常复杂,所以在研究的时候通常假定充液航天器的俯仰运动、液体晃动对航天器的轴向加速度的影响可以忽略。由文献[8]的研究得出,式(1)可以近似为:
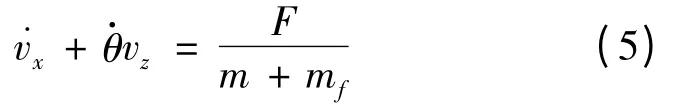
为了简化系统方程,通过以下步骤转换控制输入,令:
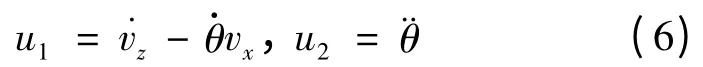
对式(2)~(4)进行变换得:
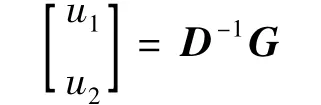
其中:

系统控制输入由f 和M 转化成为(u1,u2),式(2)~(4)可简化为:
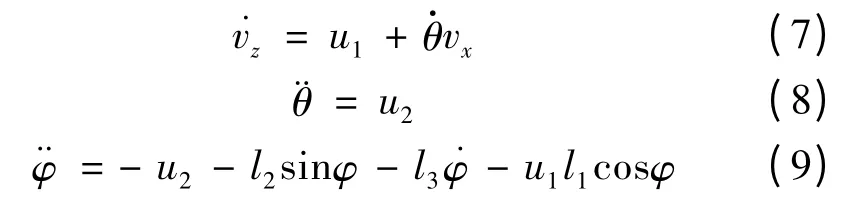
其中:
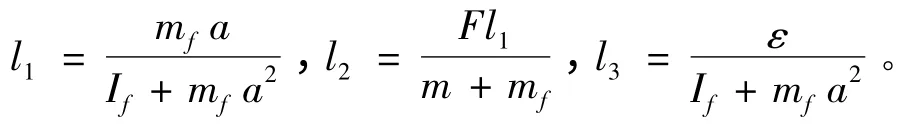
由此,可在简化以后的系统上设计控制器以及滑模观测器。
2 非线性控制器设计
由于本次研究的重点是液体晃动角的状态观测问题,所以采用已有的控制器。该控制器采用基于Lyapunov 函数的设计方法,根据Lyapunov 函数稳定性原理得出。由文献[9]可得到以下的Lyapunov函数:

对其求导后得到:
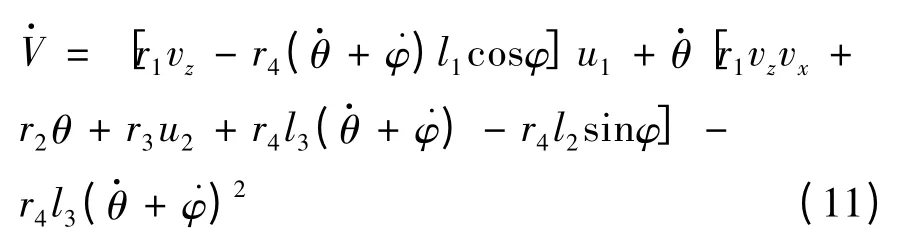
令:

则:

式中,k1,k2为正常量,一定小于0,满足稳定性原理。经过仿真验证,该控制器可以有效抑制液体晃动,并且可以很好地稳定航天器姿态,如图2 ~4,其中的参数选取如下:m = 600kg,mf= 100kg,If=90kgm2,a = 0.32m,b = 0.25m,F = 500N,ε =0.0019,r1= 10-7,r2= 10,r3= 100,r4= 0.01,k1=500,k2= 100。

图2 控制器u1,u2
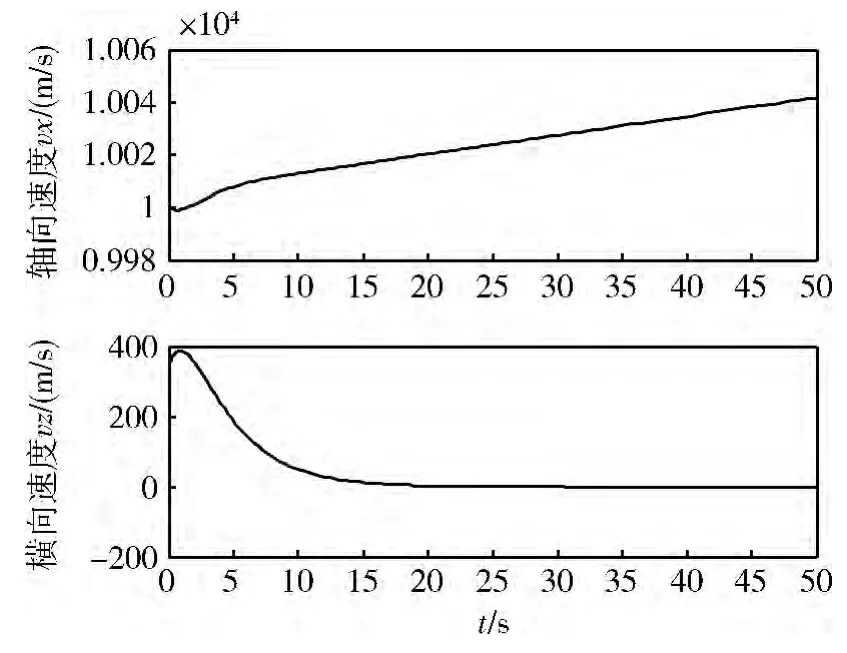
图3 施加控制器后的vx ,vz

图4 施加控制器后的θ,φ
3 针对充液航天器系统设计滑模观测器
3.1 滑模观测器结构
滑模观测器的设计采用文献[14]中的方法,该方法可以适用于部分状态不可测量的非线性系统。在本文中,状态vz,vx,θ 可测量,液体晃动角φ不可测量。在本节中,设计的这种滑模观测器通过测量vz,vx,θ 的状态,可以有效估计出液体晃动角φ。
首先,令:x1= θ,x2=,x3= φ,x4=。估计值分别为:
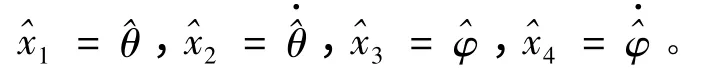
状态误差为:

滑模观测器结构为:
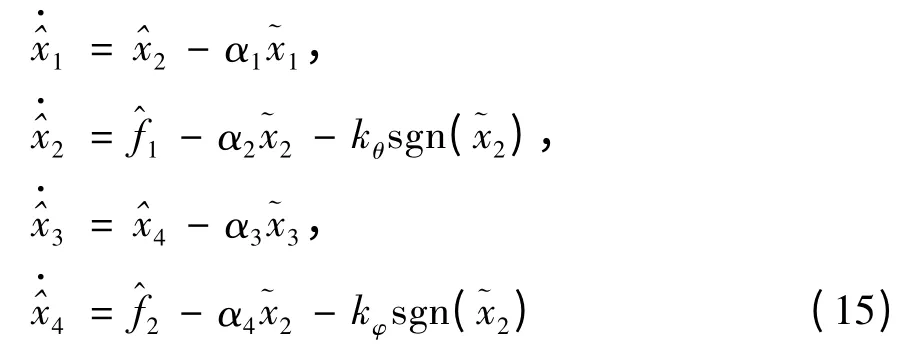
其中:
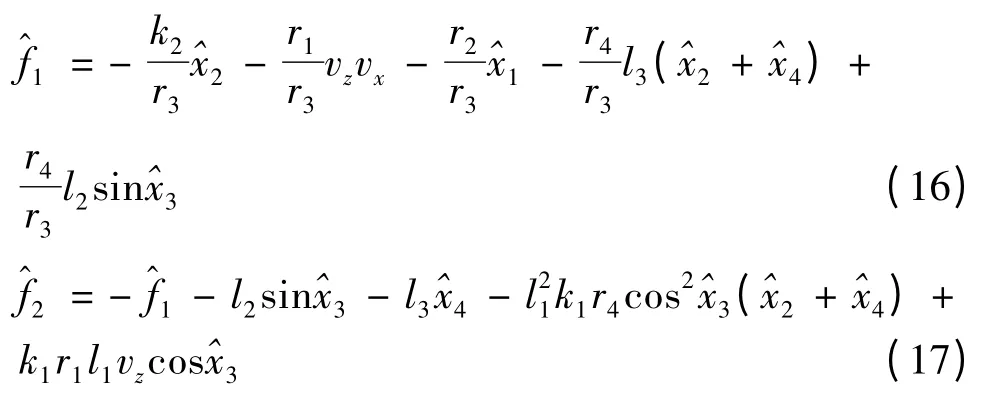
α1,α2,α3,α4,kθ,kφ都为正实数。sgn 为符号函数,其作用为指出参数的正负号,即:
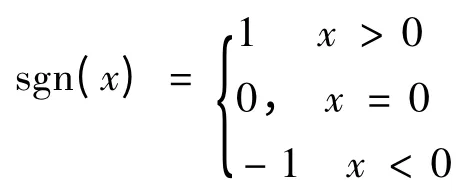
由观测器结构可得出误差方程为:
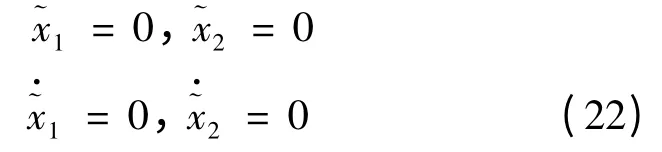
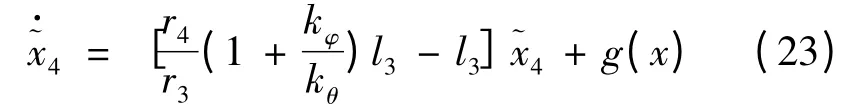
其中:

3.2 有界性说明
为了证明式(23)能使晃动角误差收敛在一定的范围内,必须说明g(x)的有界性。首先将g(x)第3 项中括号内的变换为以下形式:
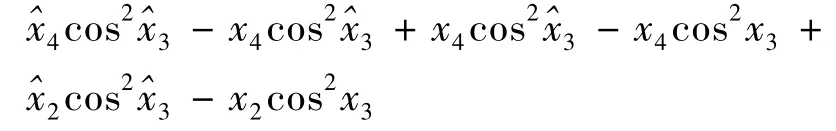
前2 项合并后可写为:
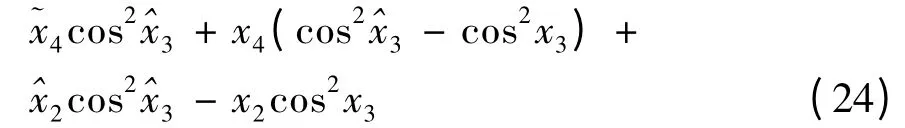
将式(24)代入g(x),可得:
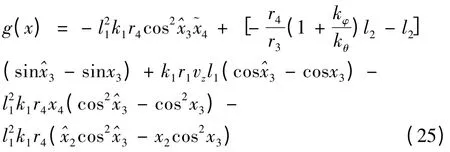
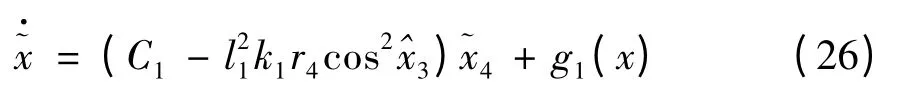
其中:
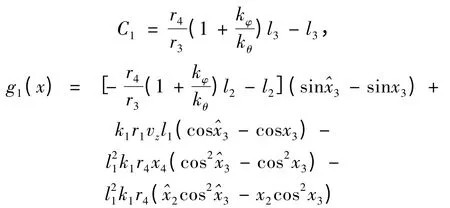
3.3 误差范围分析
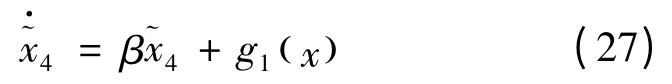
其次,由前面分析可知g1(x)有界,则可令d 为一正常数,结合式(20),不可测部分误差如下:
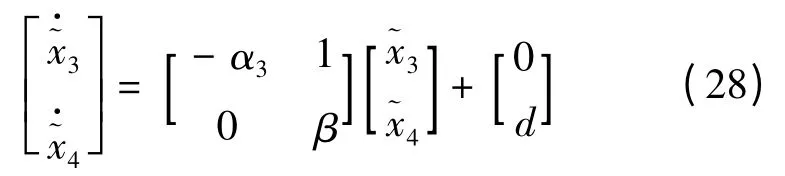
误差范围分析采用系统状态运动规律,对初始时刻t0= 0 情形具有表达式:
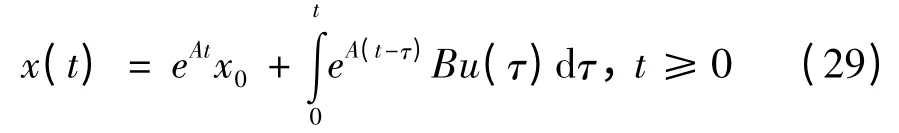
采用预解矩阵法,通过给定的2 × 2 矩阵A,定出预解矩阵(sI -A)-1,对其取拉普拉斯反变换,得出eAt的算式为:
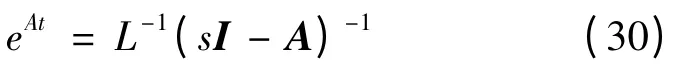
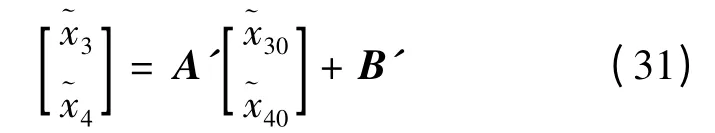
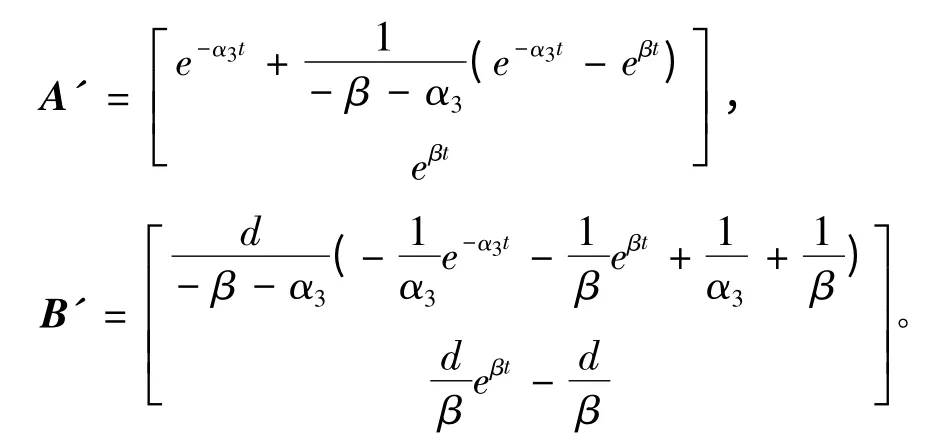
其中:可见,当t 趋向于无穷时:
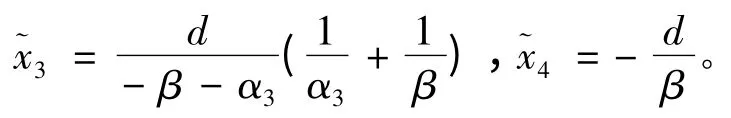
可知,观测误差有界,在仿真中,由于g1(x)的范围d 数值较小,所以误差近似于0。
3.4 仿真
仿真中,相关参数为:m = 600kg,mf= 100kg,If= 90kg/m2,a = 0.32m,b = 0.25m,F = 500N,ε =0.0019,r1= 10-7,r2= 10,r3= 100,r4= 0.01,k1=500,k2= 100,α1= 1,α2= 2,α3= 0.4,α4= 1,kφ= 0.1,kθ= 0.1。
系统初始值为:vz0=350m/s,φ0=30°,vx0=10000m/s,
对滑模观测器进行仿真验证,图5 为晃动误差角的仿真图;图6 为晃动角和晃动估计角的仿真图;图7 为晃动角速率误差的仿真图;图8 为替换了晃动估计角后的简化系统控制器u1,u2;图9 为将晃动估计角代入简化系统后得到的vx,vz;图10 为姿态估计角仿真图。

图5 晃动误差角
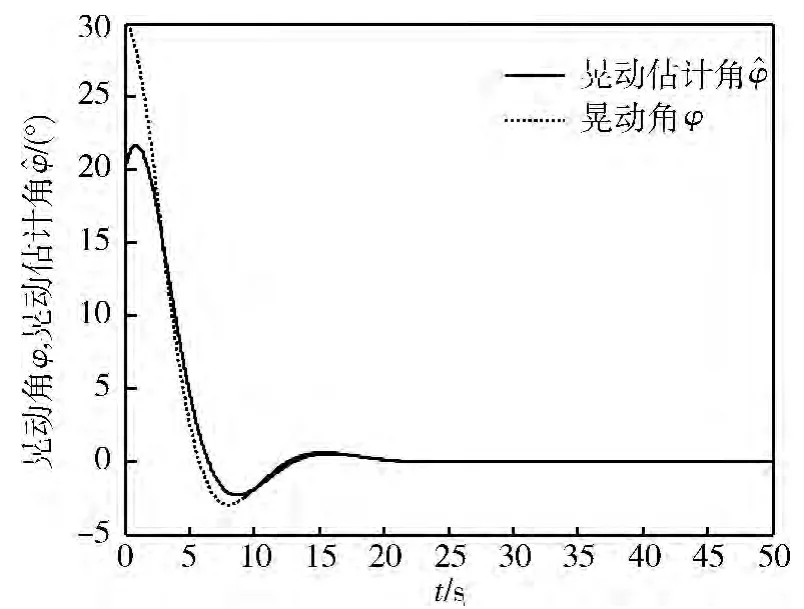
图6 晃动角φ,晃动估计角

图7 晃动估计角速率
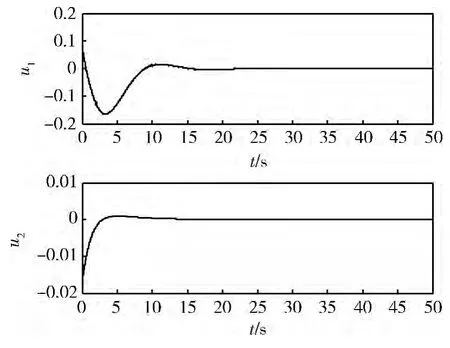
图8 将 代入简化系统得出的u1,u2

图9 将 代入简化系统得出的vx,vz
由仿真图可见,这种滑模观测器的设计方法可以应用于充液航天器系统。图5 ~7 表明,晃动角估计值能快速跟踪实际值,且误差较小;图8 ~10 表明,使用晃动估计角替换原晃动角的系统可以有效地稳定航天器的姿态,在很短的时间内使横向速度vz、姿态角θ 趋近于0。
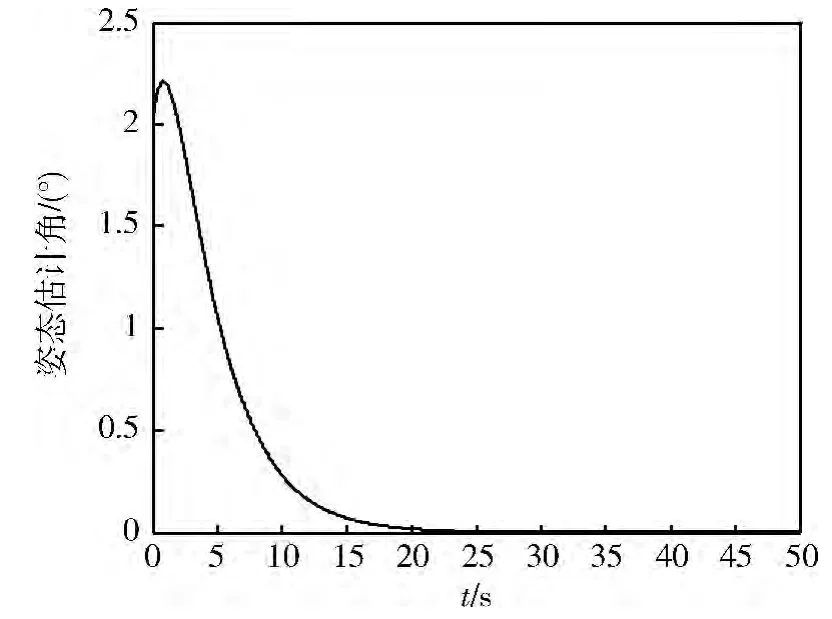
图10 姿态估计角
4 总结
本文针对液体晃动等效单摆角实际中不可测量的特点,设计了滑模观测器,利用可测状态间接求得了晃动估计角。该方法可以将估计误差收敛于一个有界的范围内,求得的估计角在已有的控制器内也可以稳定航天器姿态,同样可以达到控制要求。最后的仿真实例说明了该观测器可以在一定误差范围内估计液体晃动角。
[1]张芳謇. 火箭燃料[J]. 石油炼制与化工,1958(2):48-49.
[2]尹立中,王本利,邹经湘. 航天器液体晃动与液固耦合动力学研究概述[J].哈尔滨工业大学学报,1999,31(2):118-122.
[3]Qi N,Dong K,Wang X,Li Y,Spacecraft propellant sloshing suppression using input shaping technique[C]//Computer Modeling and Simulation. Macau:International Conference on ICCMS,2009:162-166.
[4]Gerrits J. Dynamics of Liquid-Filled Spacecraft:Numerical Simulation of Coupled Solid-Liquid Dynamics[D].University of Groningen,the Netherlands,2001.
[5]Shageer H,Tao G. Modeling and Adaptive Control of Spacecraft with Fuel Slosh:Overview and Case Studies[C]. AIAA Guidance,Navigation,and Control,Hiton-Head,South Carolina,August 20-23,2007.
[6]梁琼,岳宝增,于丹. 充液航天器目标跟踪自适应控制[J]. 空间控制技术与应用,2011,37(1):40-44.
[7]杜辉,张洪华. 一类带液体晃动航天器的姿态控制[J].空间控制技术与应用,2010,36(2):25-30.
[8]Cho S,McClamroch N. H,Reyhanoglu M. Feedback Control of a Space vehicle with Unactuated Fuel Slosh Dynamics[C]. AlAA Guidance,Navigation,and control Conference and Exhibit,Denver,CO,August 14-17,2000.
[9]Reyhanoglu M. Maneuvering control problems for a spacecraft with unactuated fuel slosh dynamics [C].IEEE Proceedings of Conference on Control Applications,2003:695-699.
[10]Reyhanoglu M,Hervas J R. Nonlinear control of space vehicles with multi-mass fuel slosh dynamics[C]. IEEE 5th International Conference on Recent Advances in Space Technologies,Istanbul,Turkiye,2011:247-252.
[11]Reyhanoglu M,Hervas J R. Nonlinear control of a spacecraft with multiple fuel slosh modes[C]. IEEE 50th Conference on Decision and Control and European Control Conference,Orlando,FL,USA,2011:6192-6197.
[12]祝乐梅,岳宝增.充液航天器姿态的自适应非线性动态逆控制[J]. 动力学与控制学报,2011,9(4):321-325.
[13]王伟,易建强,赵冬斌,刘殿通.Pendubot 的一种分层滑模控制方法[J]. 控制理论与应用,2005(3):417-422.
[14]Slotine J J E,Hedrick J K,Misawa E A. On sliding observers for nonlinear systems[C]. American Control Conference,Seattle,WA,June 1986.
[15]Slotine J J E,Sastry S S. Tracking control of nonlinear systems using sliding surfaces,with application to robot manipulators[J]. Int. J. Control,1983,38(2):465-492.
[16]Haojian Xu,Maj D.Mirmirani,and Petros A.Ioannou.Adaptive sliding mode control design for a hypersonic flight vehicle[J]. Journal of Guidance Control And Dynamics,2004,27(5):835-836.
[17]顾黄兴,齐瑞云.带液体晃动航天器的非线性自适应反馈控制[J]. 航天控制,2013,31(4):72-77. (Gu Huangxing,Qi Ruiyun. Nonlinear adaptive feedback controller for spacecraft with fuel slosh[J]. Aerospace Control,2013,31(4):72-77.)
[18]顾黄兴,齐瑞云.一类充液航天器的非线性自适应反馈控制[C].中国控制会议,2013.
