基于观测器的高超声速飞行器模糊自适应控制*

王永超 张胜修 曹立佳 扈晓翔

第二炮兵工程大学，西安710025

高超声速飞行器是指飞行速度大于5 倍音速的有翼或无翼飞行器，具有速度快，反应时间短和突防能力强等诸多优点［1］。与传统飞行器相比，高超声速飞行器采用的机身一体化设计，气动特性快速变化，使得快时变，强不确定性和强耦合等特征表现的更为突出。复杂的动力学特性，未知的飞行环境和严格的控制要求使得控制系统必须具有很强的鲁棒性和适应性，这些都给控制系统的设计提出了前所未有的挑战［2－3］。

近年来，国内外学者积极投身于高超声速飞行器控制器设计的浪潮之中，并且取得了许多十分有意义的成果。文献［4］将滑模控制与动态逆控制相结合，有效地解决模型不确定性问题。文献［6］针对弹性体的高超声速飞行器，基于所提出的鲁棒滑模面和误差跟踪模型，设计了一种自适应滑模控制器。文献［7］针对高超声速飞行器执行器的饱和控制问题，提出了一种模型参考自适应切换控制方法。文献［8］充分利用神经网络具有很强的学习能力和自适应能力的特点，设计了自适应反演控制系统。文献［9］提出了一种基于T-S 模糊系统的容错控制方法。

以上方法在解决高超声速飞行器的建模与控制的部分问题上，取得了较好的效果，但是未综合考虑非线性条件下高超声速飞行器参数的不确定性和外部干扰等问题。

在具有外界干扰和参数不确定的情况下，为了提高控制精度，选用具有物理意义明确、易于工程实现的干扰观测器技术，可逼近不确定系统中的干扰［10］。自适应模糊方法可以以任意精度逼近任意光滑非线性系统［11］，非常适用于非线性多变量复杂系统的控制问题，并且具有很强的鲁棒性。分层模糊系统［12］能够减少在线辨识参数的数量，有效解决“维数灾难”问题。但是目前所研究的NDO 要求干扰变化很慢，甚至要求为0，采用这种观测器用于估计高超声速飞行器的外界干扰显然是不合适的。自适应模糊控制方法本身具有一定的鲁棒性能，但是在外界干扰变化很快的情况下，效果明显变差。

本文将利用模糊系统在线逼近高超声速飞行器的非线性模型，利用NDO 在线估计外界干扰，对逼近误差进行补偿，为有效克服传统干扰观测器的限制条件，设计鲁棒补偿控制项，提高系统在干扰快速变化条件下的鲁棒性。所得结果通过Lyapunov 理论进行验证。

1 高超声速飞行器模型

1.1 纵向模型

本文将采用通用的高超声速飞行器纵向通道模型，具体模型如下:

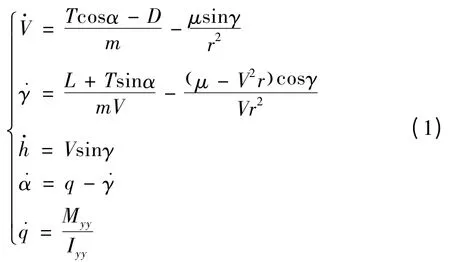
式中，V，γ，h，α，q 分别表示飞行过程当中的速度、航迹倾角、高度、攻角和俯仰角;T，D 和L 分别表示所受到的推力、阻力和升力;Myy，Iyy和m 表示俯仰转动力矩、转动惯量和质量。

L，D，T，Myy的计算表达式，气动参数在平衡点附近的包含不确定参数的拟合计算式以及发动机动力学模型详见文献［4］。

1.2 精确反馈线性化

取状态向量X = ［Vγ α β h］T，控制输入向量为U =［βcδe］T，输出向量为y =［V h］T，基于精确反馈线性化理论可将高超声速飞行器的纵向模型进行反馈线性化，得到的结果如下:

系统存在外部干扰的情况下，式(2)可变为:

式中，D =［d1d2］T为系统所受到的未知外部干扰，假设外部干扰有界。具体推导过程见文献［4］。

本文研究的是巡航状态下存在强干扰条件下高超声速飞行器鲁棒控制问题。

2 非线性干扰观测器

由于系统中存在不确定性参数和较大干扰，为了减小外界干扰对控制系统的影响，提高控制精度，引入非线性干扰观测器(NDO)估计系统干扰。

设计NDO 如下:

为了简化设计，文中选择L = diag{L1，L2}，且满足L1，L2＞0 。则令其估计误差为:

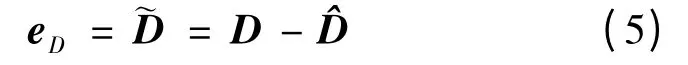
假设1:对于不确定性系统(3)存在的干扰，存在未知正常数χ 和ϑ，使得‖D‖2≤χ 和‖‖2≤ϑ在时间域 [ 0∞ )上成立，则NDO 估计误差eD将渐进收敛到一个有限半径的闭球内［10］，且半径满足:

3 自适应模糊H∞控制器设计

定义系统跟踪误差向量e =［Vd－V，hd－h］T，以速度V 通道为例，选取常数s0＞0，令sk= hks0(k =1，2)，1 = h1＜h2，作Hurwitz 多项式:

则速度V 和高度h 滤波跟踪误差为:

由文献［4］可得:

从式(9)显然可以看出，当γ ≠90°时，det(G)≠0 。则依据［5］得到系统的模糊控制器:

同时根据NDO 的输出，对系统干扰进行补偿，得到修正后的控制器:

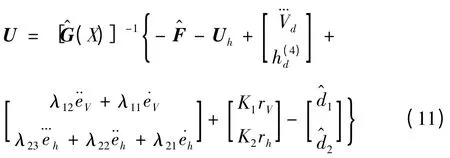
为了得到如式(11)所示的模糊控制器，需要构造分层模糊系统。

3.1 分层模糊系统构造

文献［5］给出了一个具有n个输入变量的分层模糊系统的结构。根据以下步骤构造第i(i = 1，2，…，n －1)层模糊系统:

Step1:对第i 层模糊系统中的变量yi－1，xi+1分别定义集合(l = 1，2，…，Li，Li为第i 层模糊系统规则库中的IF-THEN 模糊规则)。

Step2:根据以下Li条IF-THEN 模糊规则对第i层模糊系统进行构造。

IF yi－1是且xi是，THEN yi是El。

Step3:采用乘积推理机，单值模糊器和中心平均解模糊器，得到第i 层模糊系统的输出:

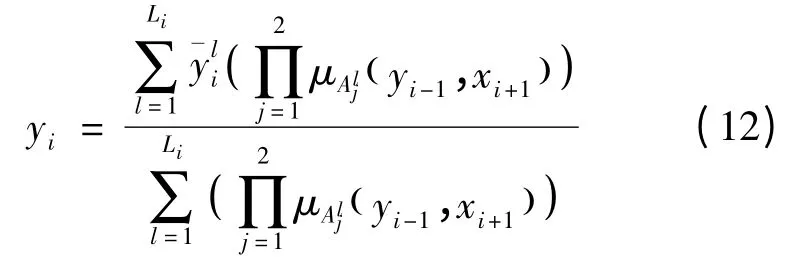
若θi表示自由参数集合，则上式可变换为:

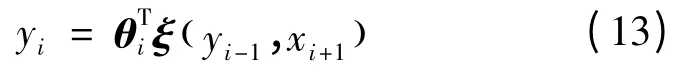
式中，ξ ( yi－1，xi+1)为一个Li维的向量，第m个向量元素为:

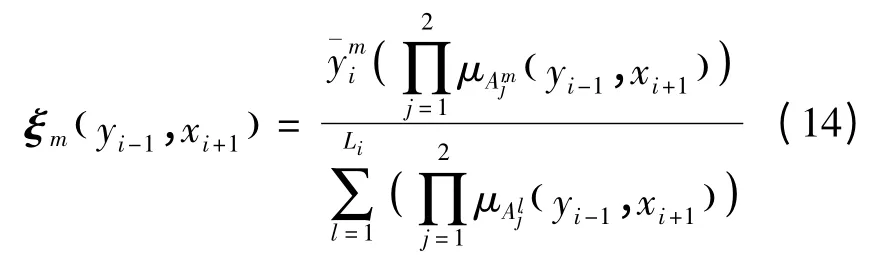
采用上述步骤，分别建立相应的模糊系统对函数fV，fh，g11，g12，g21，g22进行逼近。

模糊系统建立之后，专家知识与经验知识等其他与系统有关的知识通过初始状态自由参数确立的过程被嵌入到控制系统中。

3.2 引入鲁棒补偿项

建立的分层模糊系统存在一定的逼近误差，同时非线性干扰观测器虽然收敛有界，但是在干扰变化很大的情况下，对干扰的估计效果很差，这些都对控制系统造成影响。为此对控制器(11)进行改进，引入鲁棒补偿控制项。

若建立的系统满足如下假设:

假设2:在紧集S ⊂Rn，G(x)非奇异，且‖G(x)‖2= σ［GT(x)G(x)］≥b1＞0 。其中，σ(·)表示矩阵的最小奇异值。

假设3:系统有相对阶r =［r1，…，rm］T，并且零动态具有指数吸引性质。

假设4:系统中涉及的变量有界。

则设计如下所示模糊自适应鲁棒控制器:

控制系统工作过程中，θfV，i等参数要进行在线调整，因此需要确定参数的自适应律。同时为了克服传统NDO 的限制条件，也需要确定鲁棒补偿项的具体表达形式。

3.3 自适应律和鲁棒补偿项设计

对系统(3)而言，由式(9)可得在巡航飞行条件下，G(x)非奇异，并且飞行速度和高度分别经过3次和4 次微分之后，节流阀调定的指令信号βc和舵偏角δe出现在方程式中，则系统的相对阶为3 +4 =7，与系统阶数相同，故满足假设2 和3。

将上述控制器带入到系统(以速度通道为例)中，得:

定义参数向量的最优估计为:

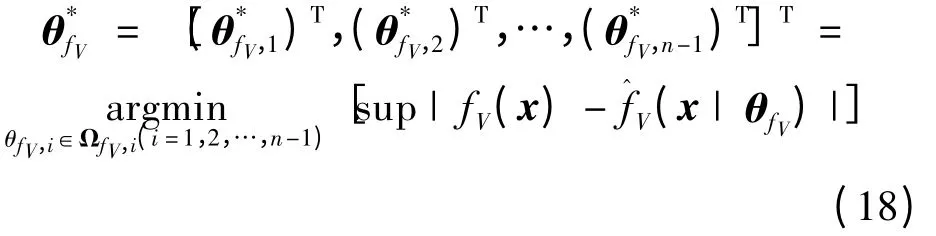
式中，ΩfV，i= {θfV，i‖θfV，i‖≤MfV，i};M*为设定的上界。类似的也可定义最优估计。

定义最小逼近误差:

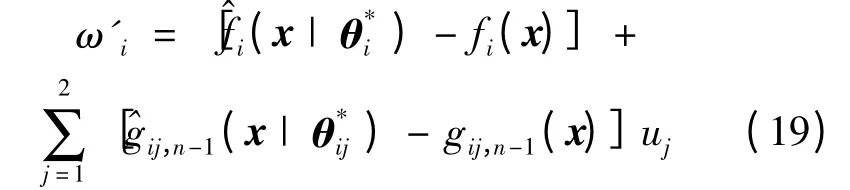
将式(19)带入到式(17)中，合并得:

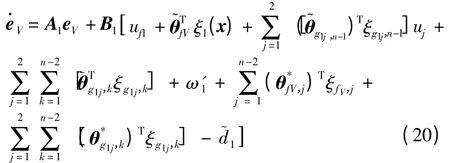
假设自由参数有界，设定组合干扰为:

选取Lyapunov 函数:

式中，αi，γ1j，k，βi，γ2j，k＞0 为设计的自适应参数。

对VV求导，并将式(20)带入，整理合并得:

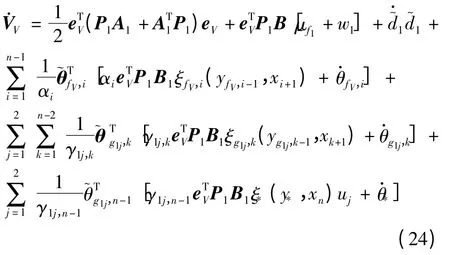
选取自由参数的自适应律为:

当i = 1，2，…，n －1 时，

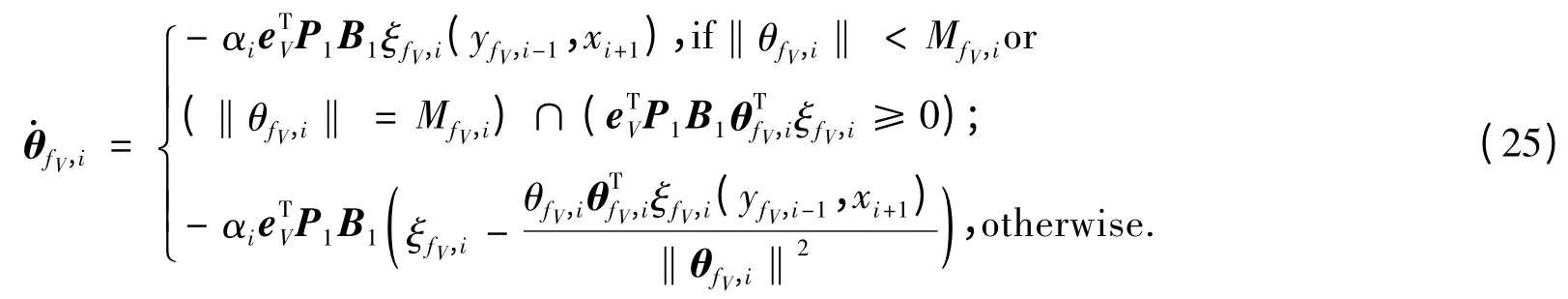
当k = 1，2，…，n －2 时，

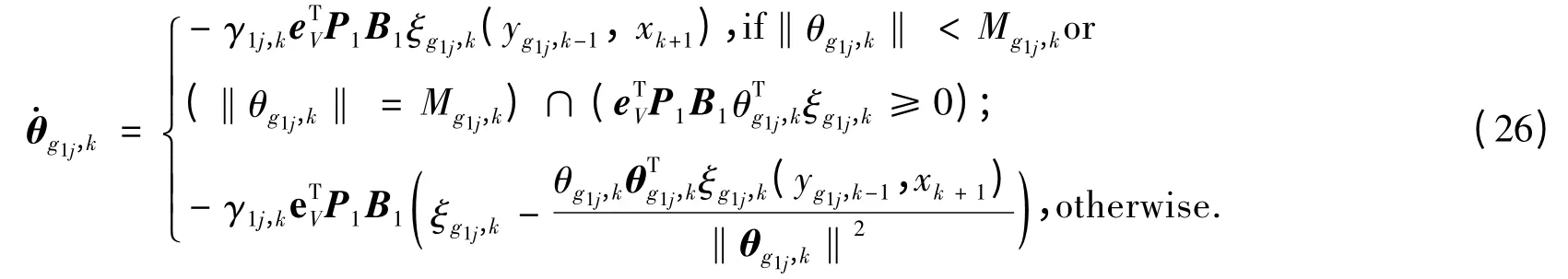
当k = n －1 时，

根据文献［5］，式(25)、(26)和(27)可以保证自由参数集的模有界，并且可以得到:

根据上述不等式，则式(24)可简化为:

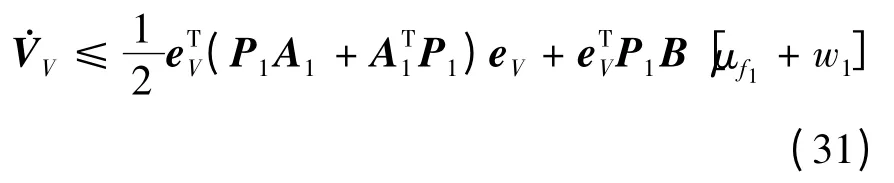
选取鲁棒补偿项为:

式中，μ1＞0 为鲁棒控制项加权因子。

令P1为如下Riccati 方程之解:

式中，ρ 为干扰抑制水平常数;Q1为正定矩阵。

将式(33)带入到式(31)，整理得到:

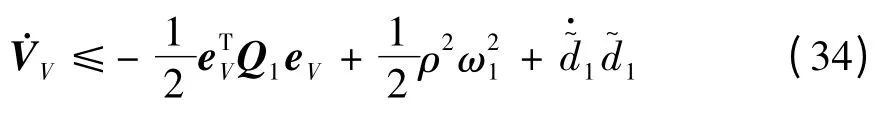
由式(4)和(5)可得:

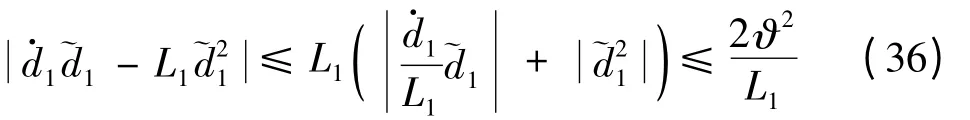
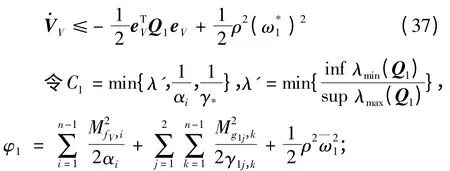
λmin(Q1)，λmax(Q1)为Q1最小和最大特征值;=sup‖‖为组合干扰的上界。对上式整理可得:

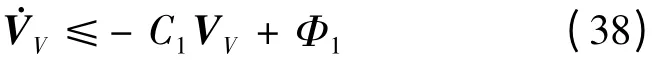
同理在高度通道上也可得到:

联立式(38)和(39)，可得:

式中，C = min{C1，C2}，Φ = 2·max{Φ1，Φ2}。

由式(38)～(40)和假设3，推得:eV，eh，X ∈L∞。

通过以上推导论证，证明设计的控制器能够使系统保持稳定。

4 仿真分析

本文针对吸气式高超声速飞行器在速度V =15060ft/s，高度h =110000ft 的飞行条件下，结合MATLAB 对控制系统进行仿真研究。飞行器的初始平衡状态数据参见文献［4］。

控制指令为:速度阶跃信号为100ft/s，高度阶跃信号为2000ft。分别给出了基于NDO 的分层模糊系统自适应控制方法和基于本文方法设计的控制系统的2 组仿真结果，验证鲁棒补偿项能否克服传统NDO 受到干扰变化率条件的限制。

选定俯仰轴上受到的干扰力矩为谐波干扰，数值大小3.5 ×106sin(2t)。

2 种控制方案选定的控制器参数均为:

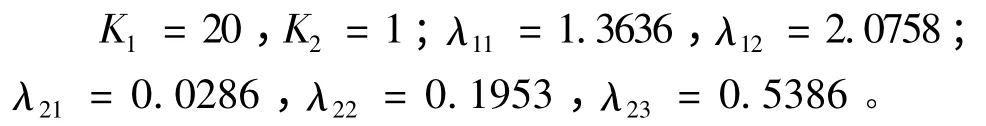
选取求解Riccati 方程中的正定矩阵为:

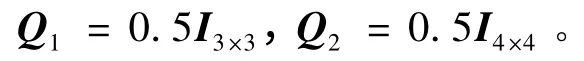
传统的鲁棒控制干扰抑制能力主要取决于干扰抑制水平常数。如果设计不当，或干扰抑制能力很差，或控制品质受到影响。本文中采用NDO 对干扰进行一定补偿，故设计干扰抑制水平常数条件相对宽松。设计鲁棒补偿项的参数为:

为防止控制输入量过大，可能导致系统不稳定，本文采用如下滤波器对指令信号进行平滑。

式中，hc和Vc为指令信号;hd和Vd为输出指令;ωn1=0.3，ωn2= 0.3，ωn3= 0.28，ωn4= 0.2，ζc= 0.95。

图1 和2 分别表示2 种方案的仿真曲线。从图1 中可以看出方案1 不能实现对高度指令的跟踪，在干扰变化率较高的条件下这种控制方法鲁棒性能很差。从图2 中可以看出方案2 能够稳定地跟踪高度和速度指令，通过对节流阀开度和舵偏角的不断调整，来抑制强干扰对控制系统的影响。仿真结果表明，即使在干扰变化率较大的情况下，系统依然能够保持很强的鲁棒性能。

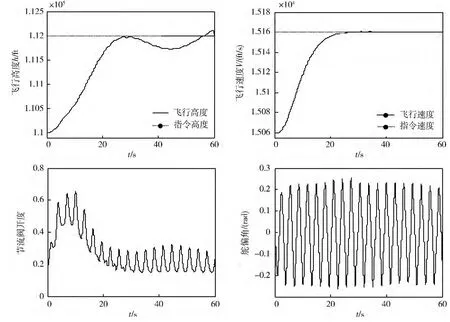
图1 基于NDO 分层模糊系统自适应控制方案

图2 基于NDO 分层模糊系统自适应H∞控制方案

5 结论

本文针对通用高超声速飞行器纵向模型，设计出了基于分层模糊系统的间接自适应控制器，减少了在线辨识参数的个数;采用NDO 对系统的复合干扰进行实时观测补偿;同时引入了鲁棒补偿控制项，克服了观测器的自身限制。根据Lyapunov 理论对系统的性能进行了分析。最后通过阶跃测试，并与基于NDO 的分层模糊系统自适应控制方案的仿真曲线进行对比，验证了设计的方法具有很强的鲁棒性能。

［1］Yu W B，Chen W C. Guidance scheme for glide range maximization of a hypersonic vehicle，AIAA-2011-6714［R］. Reston:AIAA，2011.

［2］崔尔杰. 近空间飞行器研究发展现状及关键技术问题［J］.力学进展，2009，39(6):658-673.(CUI Erjie.Research statutes，development trends and key technical problems of near space flying vehicles［J］. Advances in Mechanics，2009，39(6):658-673.)

［3］Morelli E A，Derry S D，Smith. Aerodynamic parameter estimation for the X-43A from flight data，AIAA-2005-5921［R］. Reston:AIAA，2005.

［4］Xu H J，Mirmirani M D，Ioannou P A.Adaptive sliding mode control design for a hypersonic vehicle［J］.Journal of Guidance Control and Dynamics，2004，27(5)，829-838.

［5］孙多青，霍伟.基于分层模糊系统的间接自适应控制［J］.北京航空航天大学学报，2003，29(4):303-307.(Sun Duoqing，Huo Wei. Indirect adaptive control based on hierarchical fuzzy systems［J］. Journal of Beijing University of Aeronautics and Astronautics，2003，29(4):303-307.)

［6］Hu X X，Wu L G，Hu C H，Gao H J. Adaptive sliding mode tracking control for a flexible air-breathing hypersonic vehicle［J］. Journal of the Franklin Institute，2012，349(2):559-577.

［7］Dong C，Hou Y，Zhang Y，et al. Model reference adaptive switching control of a linearized hypersonic flight vehicle model with actuator saturation［J］. Proceedings of the Institution of Mechanical Engineers，Part I:Journal of Systems and Control Engineering，2010，224(3):289-303.

［8］Xu B，Pan Y P，Wang D W，et al. Discrete-time hypersonic flight control based on extreme learning machine［J］. Neurocomputing，2014，128(3):232-241.

［9］Shen Q，Jiang B，Cocquempot V. Fault-tolerant control for T – S fuzzy systems with application to near-space hypersonic vehicle with actuator faults［J］. IEEE Transactions on Fuzzy Systems，2012，20(4):652-665.

［10］蒲明，吴庆宪，姜长生，等.新型快速Terminal 滑模及其在近空间飞行器上的应用［J］. 航空学报，2011，32(7):1283-1291. (Pu Ming，Wu Qingxian，Jiang Changsheng，et al. New fast terminal sliding mode and its application to near space vehicles［J］. Acta Aeronautica et Astronautica Sinica，2011，32 (7):1283-1291.)

［11］Wang L X. Fuzzy Systems are universal approximators［C］. Proc. IEEE International Conf. on Fuzzy Systems，San Diego，1992:1163-1170.

［12］Joo M G，Lee J S. A class of hierarchical fuzzy systems with constraints on the fuzzy rules［J］. IEEE Transaction on Fuzzy Systems，2005，13(2):194-203.