反导预警雷达部署方案的评价与优选

刘 健 管维乐 姚澎涛

空军工程大学防空反导学院，西安710051

早期预警雷达是指用于早期监视、发现弹道导弹的大型远程雷达。跟踪雷达主要用于弹道中、末段的目标跟踪，又称目标指示雷达。跟踪雷达也具备一定的预警能力。本文研究的反导预警雷达指的就是上述二类雷达。

关于雷达部署，国内外文献已做过不少的研究［1－5］，但基本都是面向防空、面向技术角度，针对反导需求的雷达部署研究资料较少，主要有文献［6 －7］对反导目标指示雷达的相关部署要求进行了分析，但对部署方案的评价问题没有探讨。

反导预警雷达部署要考虑的因素较多，部分因素存在冲突，例如雷达配置点离TBM 发射点较近，可得到较大的发现目标概率，但对敌方的监视面积变小。因此，选择适当的评价指标，对雷达部署方案进行评价优选，是反导预警雷达部署过程中的一个重要问题。

早期预警雷达、跟踪雷达都属于反导预警体系的重要组成部分，二者相互配合一起承担反导预警的探测跟踪任务。因此，反导预警雷达部署方案评价应从体系角度对二者进行综合评估。

1 反导预警雷达部署方案的评价指标

1.1 指标选择分析

关于雷达作战效能的评价指标有很多，但大多取决于雷达本身的性能，与部署无关。本文探讨的是雷达部署方案的评价与优选，所以只考虑与部署相关的效能指标。在给定敌情想定的前提下，反导预警雷达部署方案首先应满足基本的部署要求［6－7］，在此前提下再考虑方案的优劣。

早期预警雷达发现目标概率与雷达部署位置有关，离目标距离越近发现概率越大，越远发现概率越小，因此其发现目标概率可以作为雷达部署优劣的评价指标。

由于地球曲率的影响，雷达离目标距离越远发现目标越晚，为反导系统提供的预警时间也就越短，因此早期预警雷达提供的预警时间与雷达部署位置有关。该指标等价于发现目标时刻，因此发现目标时刻不再选入。

地形地物对早期预警雷达的遮蔽角将影响到雷达对目标的发现距离、发现时刻。虽然雷达部署时会考虑这一因素，但由于条件限制地形遮蔽有时无法避免，因此遮蔽角应作为部署评价的考虑因素。跟踪雷达探测时目标已飞得较高，因此基本不考虑遮蔽问题。

早期预警雷达、跟踪雷达都具备落点预报能力。早期预警雷达落点预报精度差，但预报时刻早;跟踪雷达落点预报精度好，但预报时刻晚。鉴于反导作战的迅捷性，这里选择早期预警雷达的落点预报精度作为评价指标，并且跟踪雷达落点预报精度与后面选取的跟踪雷达目标指示精度具有相关性，因此跟踪雷达落点预报精度不再选入。

早期预警雷达落点预报时刻与发现目标时刻(同提供的预警时间)具有较强的相关性，提供的预警时间作为评价指标已经选入，因此落点预报时刻不再选择。

早期预警雷达对跟踪雷达的目标指示精度，虽然与部署位置有关，但该指标在早期预警雷达的落点预报精度中已基本体现，故不再选入。

跟踪雷达截获目标的时刻、全程跟踪目标的时长均与其部署位置相关，应作为评价指标选入。

跟踪雷达提供目标指示的精度与部署位置相关，雷达与目标距离越近，目标指示精度越高，因此跟踪雷达提供目标指示的精度可作为评价指标。由于提供目标指示是一段过程，目标的位置是动态的，目标指示精度也在发生变化，为此可选择一个交接班的关键点作为目标指示精度的度量。

跟踪雷达与制导雷达的交接班成功率、交接班时间与跟踪雷达的目标指示精度相关，由于跟踪雷达的目标指示精度已选入，因此二者的交接班成功率、交接班时间不再选入。

反导预警雷达对空气动力目标也具备探测能力，因此应考虑雷达部署方案对防空需求的兼顾性。

1.2 评价指标选定

鉴于上面分析，选择反导雷达部署评价指标如下:1)早期预警雷达发现目标概率;2)早期预警雷达提供的预警时间;3)早期预警雷达落点预报精度;4)考虑遮蔽角时早期预警雷达对目标的最大发现距离;5)跟踪雷达截获目标的时刻;6)跟踪雷达全程跟踪目标的时长;7)跟踪雷达的目标指示精度;8)早期预警雷达对TBM 可能发射区域的监视比例;9)部署方案对防空需求的兼顾性等。

部分评价指标具有一定相关性，权重计算时应适当考虑。上述评价指标也不一定全部选择，可根据实际需要确定。

2 相关评价指标的计算

2.1 早期预警雷达发现目标概率的计算方法

雷达发现目标的概率p 可表示为

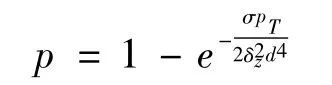
其中，p 为雷达发现目标概率，σ 为目标有效反射截面积，δz为噪声振幅的均方根值，pT为发射机功率，d 为目标距离。

由于目标距离是变化的，不便于评价，因此可选择一个关键点进行计算。对于早期预警雷达，发现目标越早越好，因此计算时目标距离可取为TBM 发射点L 到早期预警雷达配置点E 的距离。在地心大地直角坐标系下，设发射点L 的位置矢量为rL，早期预警雷达的位置矢量为rE，则雷达与目标的距离为‖rL－rE‖。在此距离下，早期预警雷达发现目标概率为

2.2 早期预警雷达提供的预警时间的确定方法

由于目标落地时已谈不上预警，因此真正起到预警作用的时间应该是使反导系统能来得及发现并拦截目标。所以，早期预警雷达提供的预警时间

其中，ΔTTBM为TBM 从发射到落地经历的总时间，Δt0为TBM 从发射到被早期预警雷达发现所经历的时间，Δt1为制导雷达对目标指示的响应时间，Δt2为火力单位系统反应时间，Δt3为从拦截弹发射到与TBM 遭遇所经历的时间，Δt4为TBM 从杀伤区高远界到落地点时间，Δtyc为反导体系的信息处理与通信所产生的时间延迟。

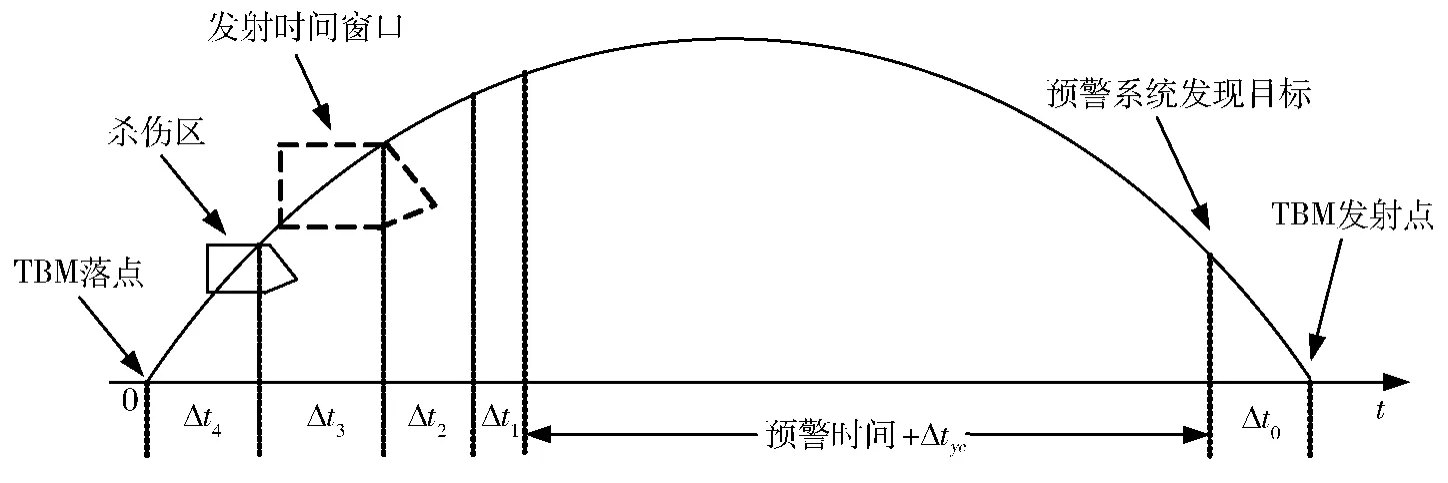
图1 预警时间计算示意图

ΔTTBM可由弹道方程求得，Δt1，Δt2为兵器指标，Δt3，Δt4由拦截弹、TBM 弹道方程求得，Δtyc由反导体系的结构性能决定。Δt0与早期预警雷达类型、性能、部署位置、部署区域海拔高度以及TBM 发射点、TBM 雷达散射截面等因素相关。

从概率角度来看，若早期预警雷达发现目标概率达到某个阈值pc，可认为雷达发现了目标。设TBM 发射时刻为0，因此Δt0的确定方法如下:

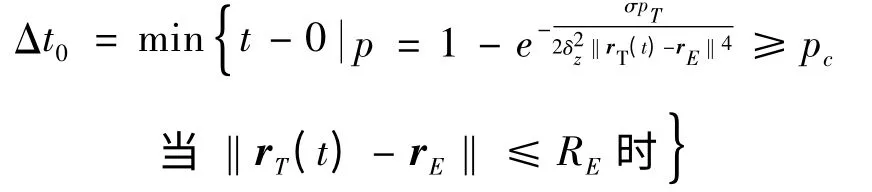
其中，rT(t)为在地心大地直角坐标系下t 时刻目标的位置矢量，RE为早期预警雷达对该目标的最大探测距离，其与早期预警雷达性能、部署区域海拔高度以及TBM 雷达散射截面等因素有关。

2.3 早期预警雷达落点预报精度的确定方法

目标距离小于早期预警雷达对其最大跟踪距离是进行落点预报的前提，即

其中，Rt为雷达对目标的最大跟踪距离，其与雷达性能参数和目标特性有关。

TBM 弹道的确定应在导弹关机后，一般应取点n 次后才能进行落点预报。对于同一条弹道来说关机时刻tgj是确定的，因此进行落点预报的最早时刻为

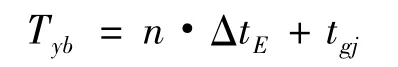
其中，ΔtE为早期预警雷达的数据周期。

可以认为，雷达的测量误差与目标距离呈正比。由于目标距离‖rT(t)－rE‖随时间t 变化，为了评价方便，对于同一条弹道来说，可选择落点预报的最早时刻Tyb为评价点，因此

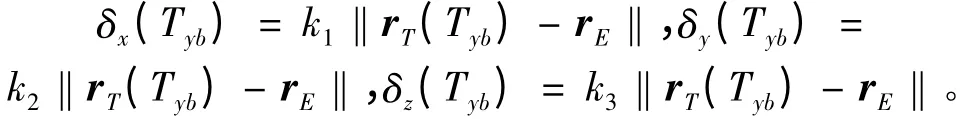
其中k1，k2和k3为相应系数，因而雷达在Tyb时刻的定位精度为

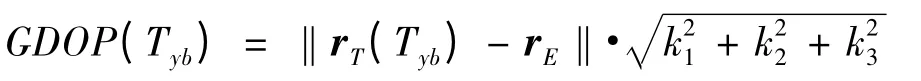
落点预报精度与定位精度直接相关，同时还与信息处理能力等因素相关，因此可认为雷达在Tyb时刻的落点预报精度为

其中，k4为相关系数，其与雷达信息处理能力等因素相关。

2.4 考虑遮蔽角时早期预警雷达对目标的最大发现距离的计算方法

考虑遮蔽角时早期预警雷达对目标的最大发现距离可按下面方法计算:

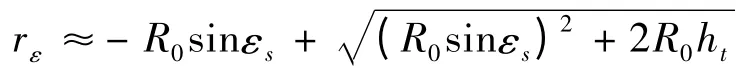
其中，R0为地球半径，εs为雷达阵地遮蔽角，ht为目标高度。

2.5 跟踪雷达截获目标时刻的确定方法

跟踪雷达截获目标时刻与雷达探测能力、部署位置、目标特性都有关系。设早期预警雷达在跟踪雷达的最大探测距离前即指示目标，因此跟踪雷达最早截获目标时刻=目标到达跟踪雷达最大探测距离时刻+跟踪雷达对目标指示的响应时间，即

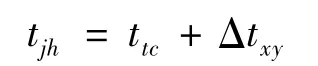
其中，tjh为跟踪雷达截获目标时刻，ttc为目标到达跟踪雷达最大探测距离时刻，Δtxy为跟踪雷达对目标指示的响应时间。ttc计算方法如下:

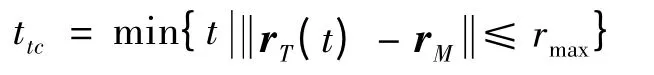
其中，rM为在地心大地直角坐标系下跟踪雷达的位置矢量，rmax为跟踪雷达对目标的最大探测距离，可由雷达方程求得。

2.6 跟踪雷达全程跟踪目标时长的计算方法

跟踪雷达对目标不再具备跟踪条件主要取决于下面因素:1)目标越过雷达最大高低角;2)目标越过雷达最大方位角;3)目标落地。

2.6.1 目标越过雷达最大高低角的判断

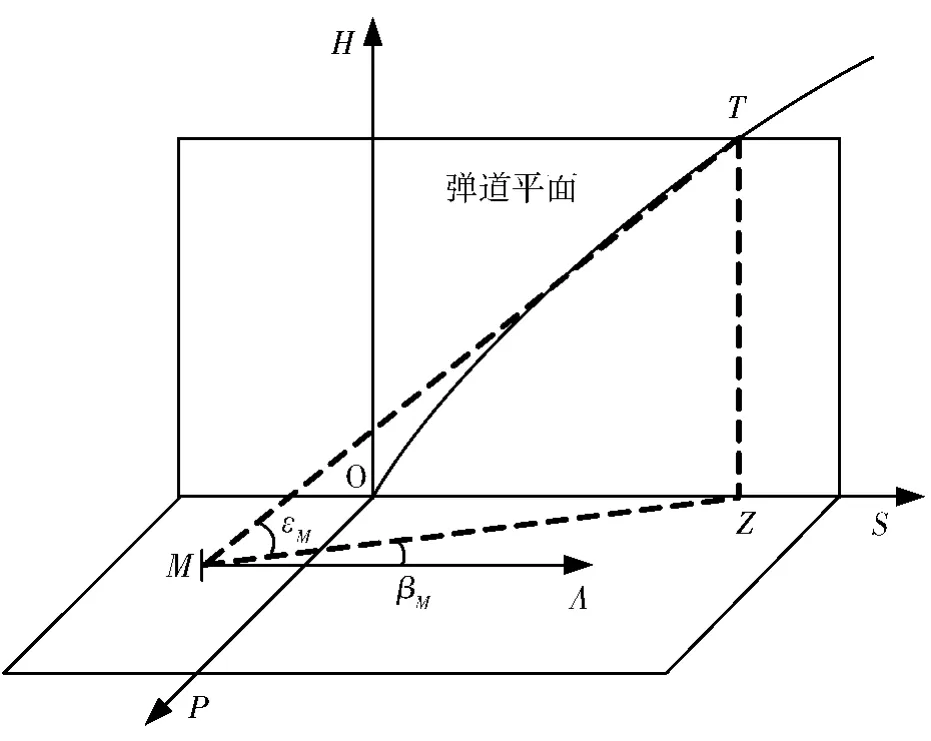
图2 高低角计算示意图

图中，M 为跟踪雷达配置点，T 为目标当前位置，Z 为目标在地面投影点，显然因此，目标越过雷达最大高低角的条件为

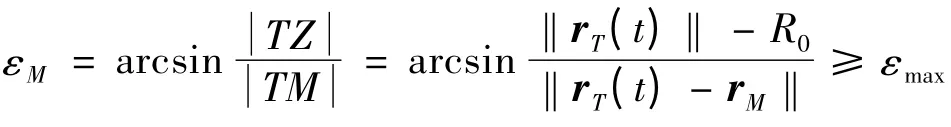
其中εmax为跟踪雷达的最大高低角。

2.6.2 目标越过雷达最大方位角的判断

在地心大地直角坐标系下，目标在地面的投影点Z 的位置矢量O0Z 为

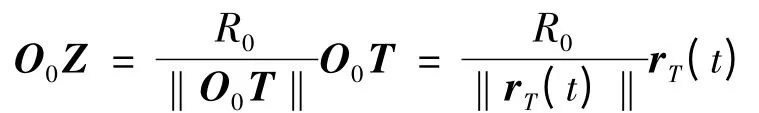
O0M 即 为 rM， 因 而 MZ = O0Z － O0M =

图3 方位角计算示意图

设MA 为雷达法线方向在地面的投影方向，对于确定的雷达部署方案来说MA 是已知的，由内积定义，可得目标相对雷达的方位角βM，因此，目标越过雷达最大方位角的条件为

其中，βmax为跟踪雷达最大方位角。

2.6.3 目标落地的判断

rT(t)为在地心大地直角坐标系下目标位置矢量，R0为地球半径，目标落地时应满足

2.6.4 跟踪雷达全程跟踪目标时长的计算

由前面分析可知，当3个条件有1个成立时，跟踪雷达不再对目标具备跟踪条件。因此，跟踪雷达结束跟踪目标时刻tjs为

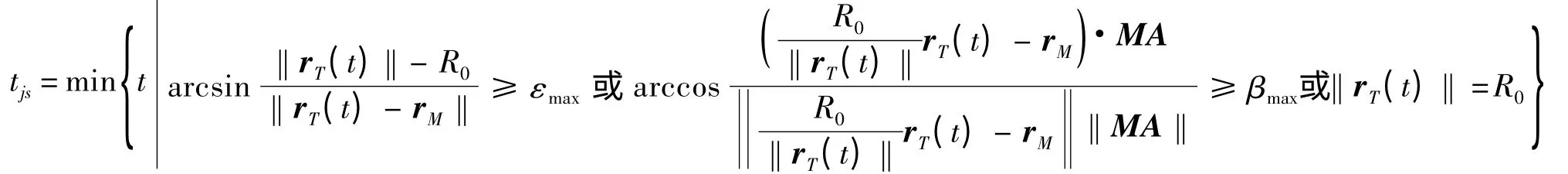
由2.5 节可得跟踪雷达截获目标时刻tjh，因而雷达全程跟踪目标时长ΔTall为

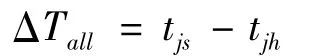
2.7 跟踪雷达的目标指示精度的确定方法

设雷达的波束宽度为θ，目标到雷达的距离为‖rT(t)－rM‖，可以认为目标指示精度与目标到雷达距离成正比，即

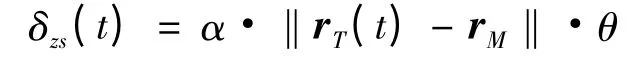
其中，δzs(t)为目标指示精度，α 为系数，其与雷达信息处理能力有关。

由于δzs(t)因目标的瞬时位置不同而不同，用于精度度量不够方便，为此须指定一个确定的点用于指示精度的计算。

由反导部署理论［8－10］可知，当要地确定和弹道确定，拦截系统和制导雷达的部署位置基本可以确定，类似2.5 中方法可得制导雷达在最大探测距离与目标弹道的交点，该交点是一个重要的目标指示点，因而跟踪雷达在该交点的指示精度具有代表性。设该交点在地心大地直角坐标系下的位置矢量为rZD，这样目标指示精度δzs可表示为

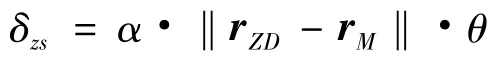
2.8 其它评价指标的计算方法

早期预警雷达对TBM 可能发射区域的监视比例涉及到监视区域的实际形状，这里不做具体讨论。

对航空目标的探测，涉及到目标的来袭方向、高度、密度、目标类型和RCS 等空袭样式的判断，不属于本文内容，因此部署方案对防空需求的兼顾性可采用人工评价法进行评估，这里不做深入探讨。

3 反导预警雷达部署方案的综合评价与优选

对于部署方案的选优，有些指标要求越大越好，有些指标要求越小越好。要求越大越好的指标有:早期预警雷达发现目标概率;早期预警雷达提供的预警时间;考虑遮蔽角时早期预警雷达对目标的最大发现距离;跟踪雷达全程跟踪目标的时长;部署方案对防空需求的兼顾性等。要求越小越好的指标有:早期预警雷达落点预报精度;跟踪雷达截获目标的时刻;跟踪雷达的目标指示精度等。

设待选的方案为n个，影响各方案综合评价值的分目标为m个。用xij表示方案j 的第i个分目标值，则n个方案的m个分目标值构成矩阵(xij)m×n。为了对部署方案进行综合评估，应将不同评价指标消除量纲，使之具有可比性，为此选择下面相对隶属度公式对xij进行归一化:

1)如果xij值越大，对应综合评价值越高，则

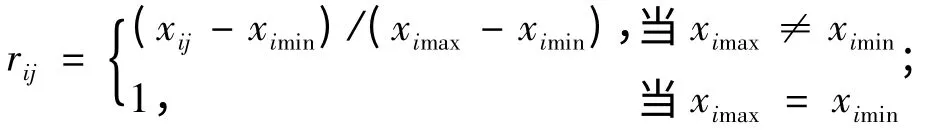
2)如果xij值越小，对应综合评价值越高，则

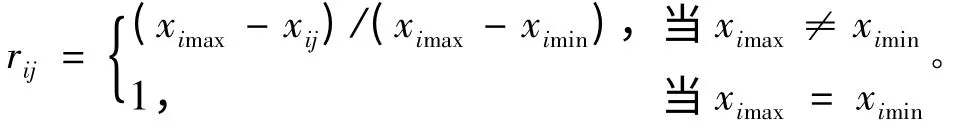
采用层次分析法计算不同类型指标的权重wi，线性加权综合，得方案j 的评价值

将Ej按由大到小的顺序排序，得到方案的优劣次序。

根据实际情况，早期预警雷达、跟踪雷达的部署方案也可分别进行评价。

上述部署方案评价方法主要针对单一弹道进行计算。对于多条弹道，可对不同弹道和方位分别进行计算，再加权综合，从而得到方案的总体评价。

4 算例

设TBM 射程为1000km，RCS =0.2m2，其飞行弹道设为最小能量弹道，总飞行时间约为562s 。设早期预警雷达、跟踪雷达主要参数如表1。

表1 早期预警雷达、跟踪雷达主要参数

以TBM 落点为原点O，建立右手直角坐标系OXYZ，X 轴指向TBM 来袭方向，Z 轴为垂直水平面向上，拟定部署方案如表2。

表2 3个部署方案

限于篇幅，2 种雷达其它参数、反导拦截系统参数、TBM 及拦截弹的弹道方程等相关数据没有列出。

选择4 项评价指标，利用层次分析法计算各项评价指标权重，如表3。采用相关模型仿真运行，按本文方法计算各项评价指标值，如表3。

表3 计算所得各方案的相关评价指标值

按本文方法计算得方案1、方案2 和方案3 的综合评价值为0.60，0.40 和0.53。因此，方案1 为最优方案。该结果与人工评价相符。

5 结语

对反导预警雷达部署的评价与优选问题进行了讨论，分析提出了反导预警雷达部署方案的评价指标，建立了不同评价指标的计算方法，给出了反导预警雷达部署方案的综合评价与优选方法，为反导预警雷达部署的评价优选提供了途径。

［1］Rustam Stolkin，Lucas Vickers，Jeffrey V Nickerson.Using Environmental Models to Optimize Sensor Placement［J］. Sensors Journal，2007，(3):319-320.

［2］Michele Garetto，Marco Gribaudo and Carla-Fabiana Chiasserini.Sensor Deployment and Relocation:A Unified Scheme ［J］. Journal of Computer Science and Technology，2008，(3):400-412.

［3］B La Scala. Multisensor Deployment Using PCRLBs，Incorporating Sensor Deployment and Motion Uncertainties［J］.Transactions on Aerospace and Electronic Systems，2006，(4):1474-1485.

［4］王万磊，李侠，周启明，王中杰. 雷达网反隐身优化部署决策模型及算法研究［J］. 现代雷达，2006，(11):8-11.(WANG Wanlei，LI Xia，ZHOU Qiming，WANG Zhongjie. Model and Algorithm of Optimal Anti-stealth Deployment of Radar Network ［J］. Modern Radar，2006，(11):8-11.)

［5］张娟，白玉，窦丽华，蔡涛.基于离散化模型的雷达优化配置与部署方法［J］.火力与指挥控制，2007，(1):22-25.(ZHANG Juan，BAI Yu，DOU Lihua，CAI Tao.A Optimized Disposition and Deployment Method of Radar Based on Discrete Model［J］. Fire Control ＆ Command Control，2007，(1):22-25.)

［6］刘健，罗亮，谢鑫. 基于方位限制的反导目标指示雷达配置要求探讨［J］. 火力与指挥控制，2013，(4):57-59. (LIU Jian，LUO Liang，XIE Xin. Study on Requests for Anti-missile Indicating Radar Disposition Based on Azimuth Restriction［J］. Fire Control ＆ Command Control，2013，(4):57-59.)

［7］白华珍，张德平，王颖龙. 地空导弹武器系统抗击TBM 时的有效部署区［J］.现代防御技术，2003，(6):24-27.(BAI Huazhen，ZHANG Deping，WANG Yinglong. Effective Deployment Area of the Surface to Air Missile Weapon System Intercepting Tactical Ballistic Missile［J］. Modern Defense Technology，2003，(6):24-27.)

［8］刘健，王颖龙，聂成. 反战术弹道导弹(TBM)战斗部署有关问题探讨［J］. 系统工程与电子技术，2001，(3):66-68. (Liu Jian，Wang Yinglong，Nie Cheng.Some Problems about Anti-TBM Disposition ［J］. Systems Engineering and Electronics，2001，(3):66-68.)

［9］刘健，罗亮.高层反导部署方法研究［J］.火力与指挥控制，2012，(9):85-88. (LIU Jian，LUO Liang. Study on Disposition Method for High-altitude Anti-missile System［J］.Fire Control ＆ Command Control，2012，(9):85-88.)

［10］刘健，管维乐，姚澎涛.特殊情形下反导杀伤区变化分析方法［J］. 航天控 制，2014，32(1):89-93. (LIU Jian，GUAN Weile，YAO Pengtao. A Method to Analyze the Change of Anti-missile Killing Zone in Special Situation［J］. Aerospace Control，2014，32(1):89-93.)