求解常微分方程边值问题的差分方法

2015-12-05郭晓晔蹇玲玲

长春大学学报 2015年8期

郭晓晔，蹇玲玲

(青岛理工大学琴岛学院基础部，山东青岛266106)

0 引言

常微分方程边值问题在空间科学与工程技术中有着重要的应用，如工程学、天文学、力学、经济学等领域中的大量数学模型，常用常微分方程边值问题来描述。除了少数特殊类型外，常微分方程边值问题的精确解很难用解析形式来表示，这样寻求用近似方法求得其数值解显得尤为重要。随着科学技术的进步，其近似解在理论和方法上都有很大的发展，并且在各个领域上的应用也越来越广泛。在微分方程的数值解法中，差分法不仅是最重要的方法之一，而且也是最有效的方法之一，具有普遍的适用性。

利用差分法求解微分方程的边值问题时，边界条件的处理方式影响着差分解的性质和精度。随意的边界处理方式可能导致差分解的发散，而巧妙的边界近似不仅保证了差分解的收敛，还使差分解具有较高的精度。本文简要阐述了差分方法的基本思想，讨论了求解常微分方程的边值问题的差分方法，并探讨了边界条件的处理方式，并将这两种处理方式的结果进行了比较。

1 常微分方程的边值问题

二阶常微分方程

常见的三种边界条件:

其中 α，β，α0，α1，β0，β1为常数，(1)与(2)构成第一边值问题，(1)与(3)构成第二边值问题，(1)与(4)构成第三边值问题。

2 差分格式的建立

差分法的基本思想是用有限个离散点构成的网格代替连续的定解区域，这有限个离散点称为网格的节点;用网格上定义的离散函数近似代替定解区域上的连续变量函数，离散函数和定解条件构成差分方程，解该方程即可得到边值问题的解在各节点上的近似值，即问题的数值解。

以第二边值问题为例，介绍二阶线性微分方程边值问题的差分方法。

其中α，β为常数，p(x)，q(x)，r(x)为连续函数。由解的存在唯一性定理知，问题(5)有唯一解［1］。

记 pk=p(xk)，qk=q(xk)，rk=r(xk)将(7)，(8)代入(5)得

上述方程的截断误差为ο(h2)

3 关于边界条件的处理

3.1 一般方法

对于边界条件y'(a)=α，y'(b)=β的处理，一般处理方式采用以下简单差商公式

其截断误差为ο(h)，比微分方程的误差ο(h2)低一阶。

由 y'(a)=α，y'(b)=β则，它们跟差分方程(5)(6)构成含有n+1个未知元y0，…，yn的n+1个线性方程组。

3.2 改进方法

由于微分方程离散化的截断误差为ο(h2)，可以利用数值微分公式对边界条件给出相同阶的误差。

将边界条件离散化，得差分方程

其截断误差为ο(h2)，与微分方程离散化的截断误差相同，因此该方法有较高的精度。将(5)(9)(10)联立，得出方程的数值解。

4 算例

为了验证所提出的方法的有效性，用该方法作了数值实验，将计算结果与解析解进行了比较。

例用差分方法解微分方程的边值问题

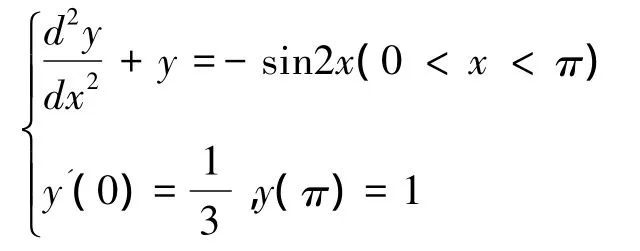
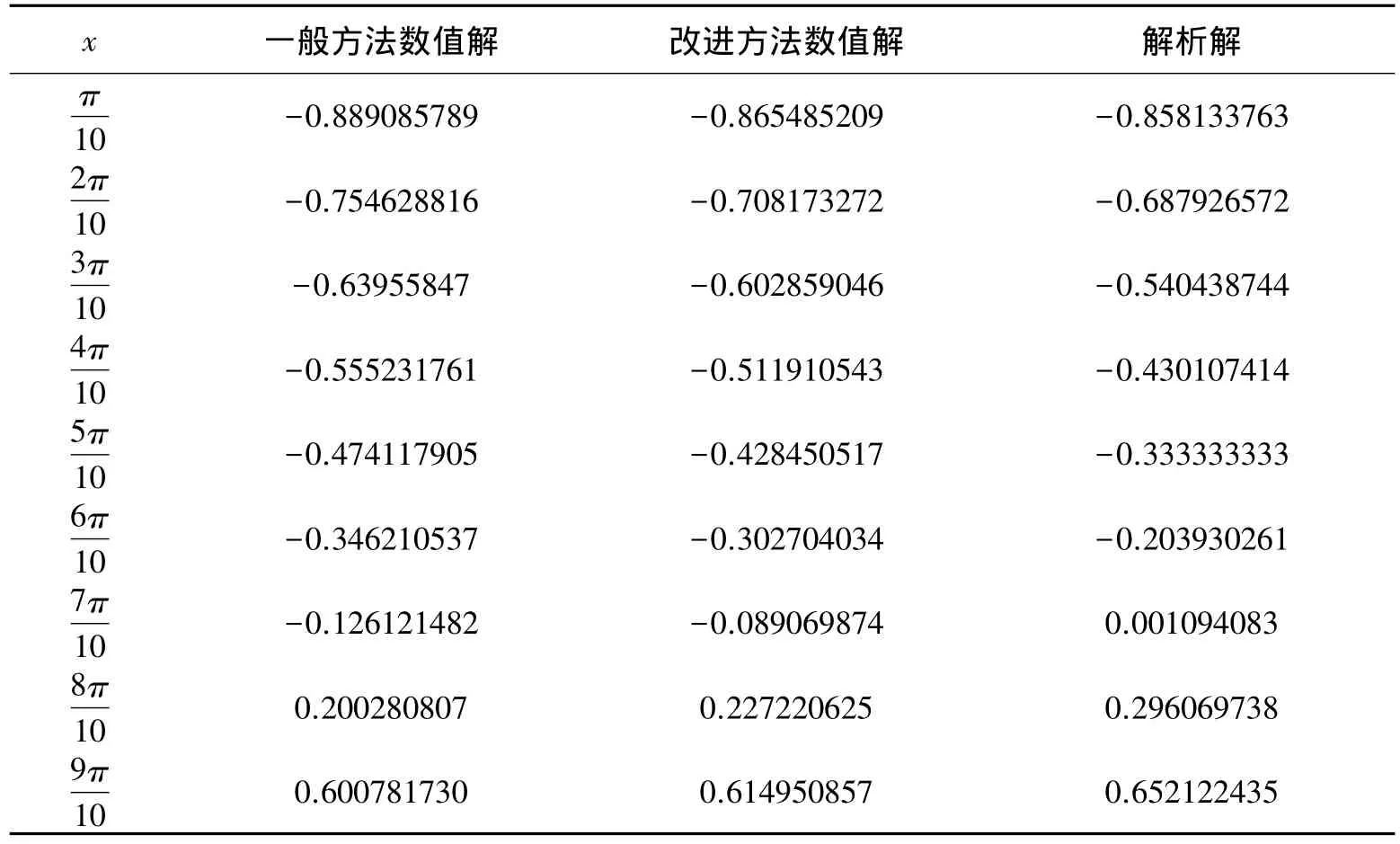
x 一般方法数值解改进方法数值解解析解π 10－0.889085789－0.865485209－0.858133763 2π 1 0－0.754628816－0.708173272－0.687926572 3π 1 0－0.63955847－0.602859046－0.540438744 4π 1 0－0.555231761－0.511910543－0.430107414 5π 1 0－0.474117905－0.428450517－0.333333333 6π 1 0－0.346210537－0.302704034－0.203930261 7π 1 0－0.126121482－0.089069874 0.001094083 8π 1 0 0.200280807 0.227220625 0.296069738 9π 1 0 0.600781730 0.614950857 0.652122435