改进的动物迁徙算法求解全局优化问题

刘金承，费佳慧

(1.长春金融高等专科学校，长春130028;2.东北师范大学计算机科学与信息技术学院，长春130117)

自20世纪80年代开始，一些看似不起眼的群居低智能的生物所表现出来的生活能力相当惊人，如:鸟群、鱼群、蜜蜂等。虽然他们的结构都很简单，但是他们之间具有相互合作的能力，是相当复杂的。这些群居低智能生物通过合作所表现出较高的“智能”，即群集智能。这种现象得到了许多学者的广泛关注，通过对这些群居低智能的生物进行模拟，提出了许多算法，如BP神经网络(Back Propagation Neural Network，BPNN)、人工免疫系统(Artificial Immune Systems，AIS)、模拟退火算法(Simulated Annealing Algorithm，SAA)、粒子群优化算法(Particle Swarm Optimization，PSO)、蚁群算法(Ant Colony Optimization，ACO)、禁忌搜索(Tabu Search，TS)、差分进化算法(Differential Evolution，DE)等如雨后春笋般不断出现。进入21世纪至今:来自于大自然的神奇灵感使得启发式算法迅速发展，各种算法百家争鸣。在世纪之初的十年间，出现了大量的改进算法，改进的思想和方法各式各样。为了提高全局优化问题的求解性能，本文提出了一种改进的动物迁徙算法来求解全局优化问题，增加寻优能力和收敛速率。我们知道带惯性权重的标准粒子群优化算法全局搜索能力很强，并且通过惯性权重W值的变化，还可以控制收敛速率的快慢。动物迁徙算法本身就具有很强寻优能力，为了进一步提高动物迁徙算法的性能，将动物迁徙算法和带权重的粒子群优化算法相结合，提出了一种改进的动物迁徙算法。

1 动物迁徙算法

1.1 灵感的来源

动物迁徙算法［1］是一种新的全局优化算法。算法的主要思想来自于无处不在的动物迁徙行为，基本上可以在所有主要的动物群体中发现。像哺乳类，鱼群，昆虫类，爬行动物类，鸟群，甲克类等。

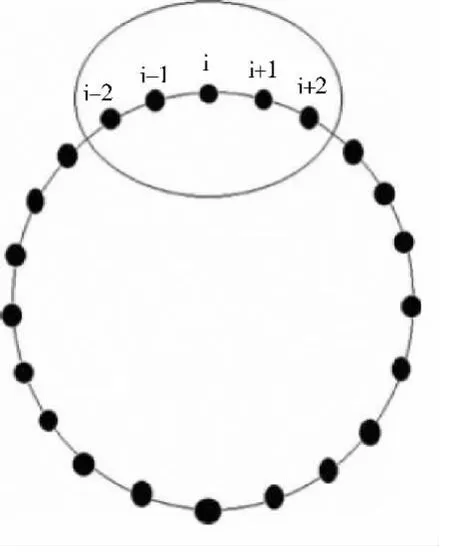
图1 环型拓扑结构

1.2 两个流程中的主要原则

在第一个流程中，动物迁徙算法模仿了动物种群从当前位置迁徙到新的位置。在这个过程中，每一个动物个体都将遵循着三个主要的规则:1)和它的邻居避免冲撞;2)和它的邻居在相同的方向上进行移动;3)和它的邻居保持紧密。对于第一个规则来说，需要每一个种群中的个体位置都是不同的。对于后面两个规则，需要动物个体通过当前位置的邻居来移动到一个新的位置上。为了定义每个个体邻居的概念，我们使用一个环型拓扑结构，如图1所示。

为了简单起见，我们设置了邻居的长度为5对于每个维度的动物个体。在动物迁徙算法中邻居拓扑是静态的，而且是定义了在一整套指数的向量。如果标志动物是i，那么邻居的组成是由i－2，i－1，i，i+1，i+2我们可以在图1中看到。如果标志动物是1，那么邻居的组成是由NP－1，NP，1，2和3。如果标志动物是2，邻居组成是由 NP，1，2，3 和 4。如果标志动物是 NP，那么动物邻居的组成是由 NP－2，NP－1，NP，1，2。如果标志动物是NP－1，那么邻居的组成是由NP－3，NP－2，NP－1和1。如果邻居的拓扑被构造，我们将随机选择一个邻居然后根据它的邻居更新个体的位置。我们通过下面的公式发现:Xi，G+1=Xi，G+δ(Xneighborhod，G－Xi，G)，Xneighborhod，G为邻居的当前位置，δ是由高斯分布的随机数生成器产生的，Xi，G+1是第i个个体的新位置。

在第二个流程中，算法模仿了动物种群在移动中是如何行动的。在种群更新过程中，一些动物可能要离开种群，而另一些动物要加入到新的种群中。动物迁徙算法假定种群总数是固定不变的。种群中的动物将要被新的个体所代替的概率为Pa。概率Pa是根据适应度fitness的好坏来决定的。对于最好的适应度fitness，被代替的概率Pa是1/NP。对于最坏的适应度fitness，被代替的概率Pa是1。每当算法产生一个新的解，算法会与 Xi，G进行评估和比较。如果 Xi，G+1的适应度 fitness比 Xi，G的适应度 fitness小，那么 Xi，G+1作为一个新的基本解;相反的，如果 Xi，G+1的适应度 fitness比 Xi，G+1的适应度 fitness大，那么 Xi，G+1将继续作为一个基本解。

1.3 动物迁徙算法的伪代码:begin

设定后代计数器的G=0;随机初始化种群Xi，人口数NP，通过适应度函数评价Xi中的每一个个体。

1.4 基于对立基学习的动物迁徙算法

曹毅和李向涛等人在2013年提出了基于对立基学习的动物迁徙算法［2］。当同时地考虑候选解在当前搜索空间和它的对立空间，通过在两个搜索空间中选择更好的个体，算法能够提供更多的机会来找到全局最优解，并且提高了算法的收敛速度。动物迁移算法自提出后在不断改进中。

2 粒子群优化算法

2.1 粒子群优化算法概述

粒子群优化算法［3］(PSO)是一种模仿我们所观察到的动物或昆虫的社会性行为(如鱼群、鸟群)的基于群体的随机优化算法。它首先是由詹姆士·肯尼迪和罗素·阿伯哈特于1995年提出。自那时起，PSO作为一种可以解决许多不同优化问题的鲁棒高效的算法，获得了越来越多的研究者所关注。在PSO中，群体中的单个粒子表示了一个潜在的解，此粒子在问题的求解空间中移动用来找到最优或者说是足够好的解。粒子将其目前所在的位置广播给它所相邻粒子。粒子的位置根据其变化的速率(速度)和与其现在所在的位置的差异(分别是其邻居找到的最佳的位置与其目前所找到的最佳的位置)而调整。由于算法是迭代的，种群越来越集中于具有高质量解的区域。

2.2 标准粒子群优化算法

Shi等在原始粒子群优化算法基础上，引入到惯性权重，提出带有惯性权重的粒子群优化算法［］，它的速度更新公式如下:

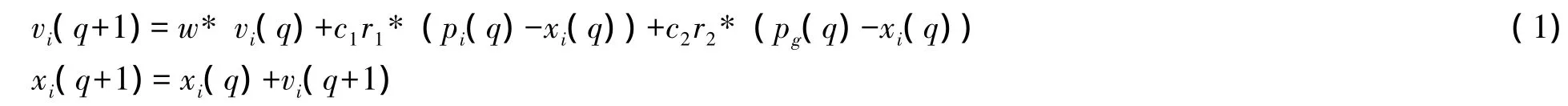
目前来说，采用较多的动态惯性权重值是Shi所提出的线性递减值(Linearly Decreasing Weight，LDW)的策略，表达式如下:

其中Tmax表示最大进化代数;Wmin表示最小惯性权重;Wmax表示最大惯性权重;t表示当前迭代次数。在大多数的应用中Wmax=0.9，Wmin=0.4。标准粒子群优化算法具有全局搜索能力强，收敛速率快等优点。

3 改进的动物迁徙算法

3.1 改进目标:寻优能力和收敛速率

动物迁徙算法全局搜索部分的公式如下:

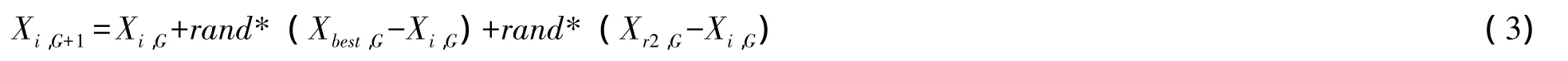
我们可以通过对公式(1)和公式(3)的对比发现，粒子群优化算法具有W*vi(q)这个重要部分，它体现了算法有较强全局搜索能力。在粒子群优化算法中，当W的值比较大时，粒子群优化算法全局搜索能力强，可以有较大的搜索的空间，可以更好地找到最优解所在的区域;当W的值比较小时，粒子群优化算法具有了较强的局部搜索能力，收敛速率高，寻优能力强，优化结果明显、精确。通过公式(1)和公式(3)，用粒子群算法替代动物迁徙算法的全局搜索部分，从而提高了动物迁徙算法的寻优能力和收敛速率。

对于怎么设置惯性权重W才能将混合动物迁徙算法的寻优能力和收敛速率发挥出来，进行了以下三次尝试。

首先将粒子群优化算法的惯性权重W设置为0.4，通过算法在23个benchmark基准测试函数上进行仿真实验的结果得出，当W=0.4时，混合动物迁徙算法具有了较快的收敛速率。但是其稳定性很差，当对适应度函数进行多次仿真实验后发现，W=0.4时的混合动物迁徙算法很不稳定，容易陷入到局部极值点。

其次考虑将粒子群优化算法的惯性权重W设置为0.9，通过算法在23个benchmark基准测试函数上进行仿真实验的结果得出，当W=0.9时，混合动物迁徙算法具有了稳定的解，但是其寻优效果很差，收敛速率缓慢。

最终，选择了线性递减的惯性权重W作为混合动物迁徙算法的W值。

通过观察公式(4)发现，当W的值比较大时，算法的全局搜索能力强，可以有较大的搜索空间，更好的找到最优解所在区域;当W的值比较小时，算法具有了较强的局部搜索能力，收敛速率高，寻优能力强，优化结果明显、精确。所以本文决定使用线性递减的惯性权重W来调节，使得混合动物迁徙算法在算法初期，具有较高的全局搜索能力，可以搜索到最优解所在的区域;算法后期又具有较高的局部搜索能力，较快的收敛速率，可以更精确的找到最优解。其中的相关参数分别有:r1，r2为［0，1］的随机数;W，c1、c2是控制速度更新公式三部分内容的权值，W称为惯性权重，c1、c2为加速因子。

3.2 改进的动物迁徙算法的流程图

改进的动行迁徒算法流程图如图2所示。

图2 改进的动物迁徙算法流程图

3.3 伪代码:begin

设定后代计数器G=0;随机初始化种群Xi，人口数NP;通过适应度函数评价Xi中的每一个个体。

3.4 函数仿真测试

为了进一步验证算法的有效性选择的23个标准测试函数在Matlab中进行实验。在这些函数中，函数f01－f13是多维问题。函数f01－f05是单峰函数，f05是在D＞3的情况下是多维函数。f06是阶梯函数有一个最小值和不连续。函数f07是一个嘈杂的二次函数当随机在［0，1］中是一个均匀分布随机数在［0，1］中。接下来的7个函数是多峰测试函数。对于这些函数来说，根据问题的规模局部最小值增大。对于许多优化问题来说，他们显然属于一类最困难的问题。函数f14－f23是低维问题，只有几个局部的最小值。对于单峰函数来说，研究者关注更多的是在收敛率方面而不是优化的最终结果;对于多峰函数来说，最终结果要比不同算法的收敛率更重要，因为他们反映了一个算法对于避免坏的最优条件的能力和去定位一个好的全局最优解。到目前为止，这些基准测试函数被广泛应用于许多研究者的不同算法中。

4 实验结果及分析

在实验分析中，将改进的动物迁徙算法(PSAMO)与传统的算法比如差分进化算法(DE)、粒子群优化算法(PSO)、生物地理学优化算法(RCBBO)、萤火虫算法(FA)［4］、动物迁徙算法(AMO)、人工蜂群算法(ABC)、布谷鸟搜索算法(CS)［5］、引力搜索算法(GSA)的数值优化问题的平均值进行比较。

4.1 单峰函数

为了体现本文所提出的改进动物迁徙算法的有效性，将改进的动物迁徙算法与差分进化算法(DE)、粒子群优化算法(PSO)、生物地理学优化算法(RCBBO)、萤火虫算法(FA)、动物迁徙算法(AMO)、人工蜂群算法(ABC)、布谷鸟搜索算法(CS)、引力搜索算法(GSA)进行比较，在解的平均值表中，f01－f05是单峰函数。对于单峰函数来说，搜索算法的收敛速率比最终结果更为重要，因为这些函数是专门为了优化单峰函数的，从算法的排名我们可以看出，虽然混合算法在单一某个测试函数中表现并不是最好的，但是在f01－f07的平均排名下，混动动物迁徙算法的排名是最好的。

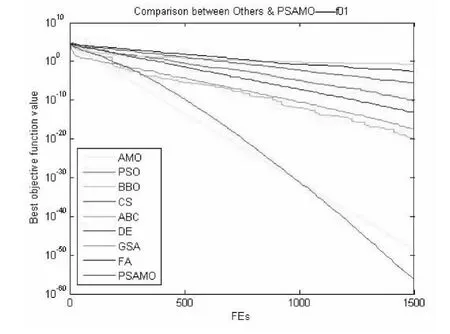
图3 对于f01函数PSAMO和其他算法性能的比较

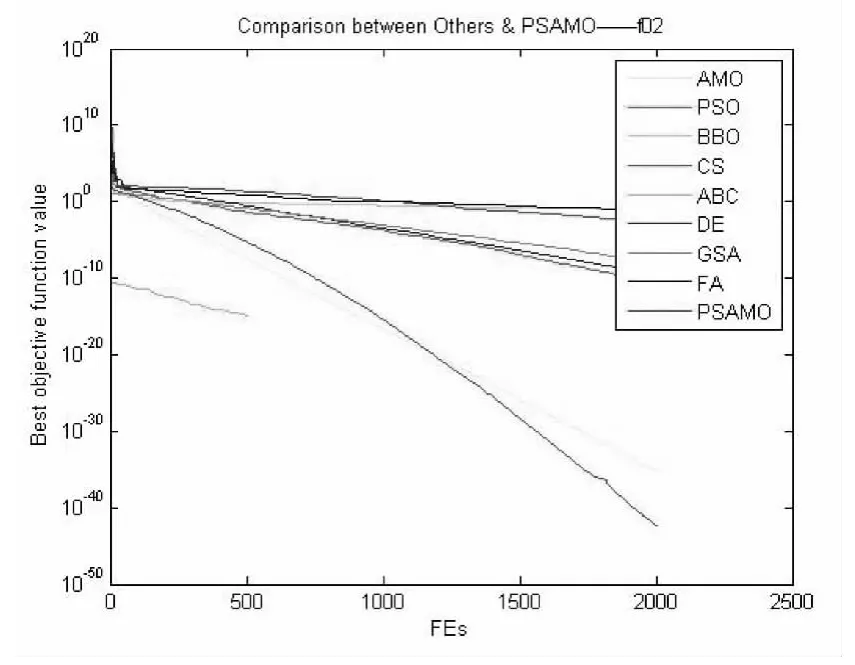
图4 对于f02函数PSAMO和其他算法性能的比较

通过从图3和图4观察混合算法的收敛速率，我们发现，在算法运行的初期，算法具有较强的全局搜索能力，可以找到最优解所在区域;在算法运行的后期，算法具有较强的局部搜索能力，可以更精确的找到最优解，从而总结出改进的动物迁徙算法具有较快的收敛速率。

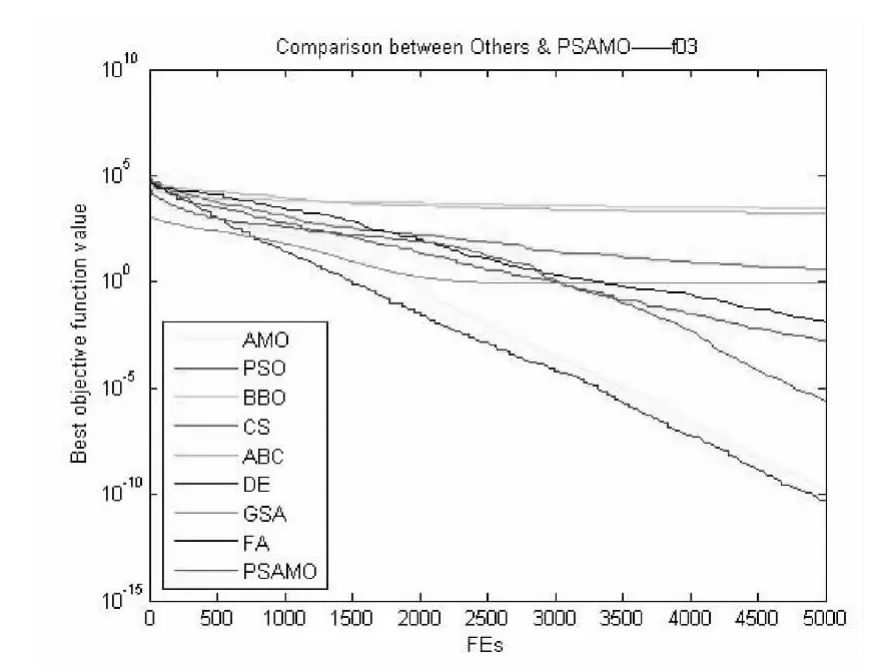
图5 对于f03函数PSAMO和其他算法性能的比较

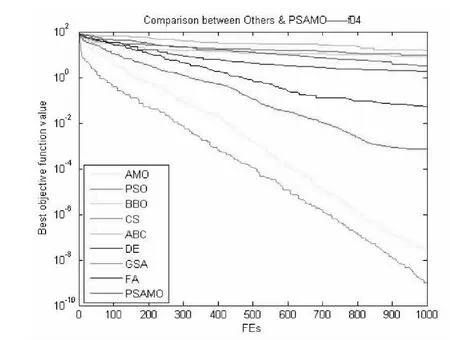
图6 对于f04函数PSAMO和其他算法性能的比较

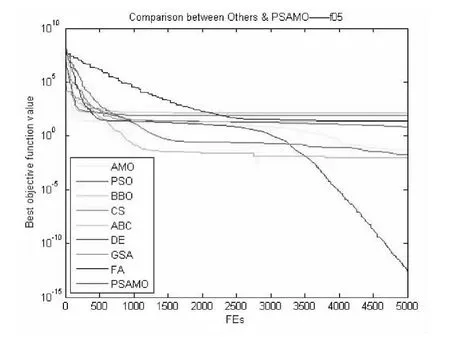
图7 对于f05函数PSAMO和其他算法性能的比较

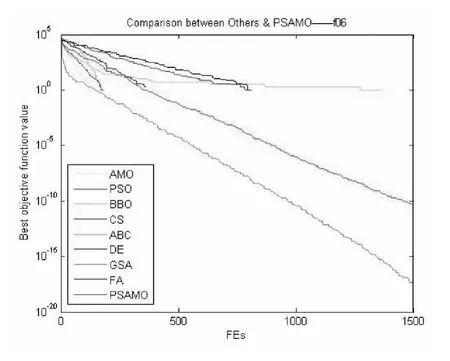
图8 对于f06函数PSAMO和其他算法性能的比较

通过对图8可以看出，PSAMO有较强的寻优能力，在算法初期便直接收敛到了全局最优解。

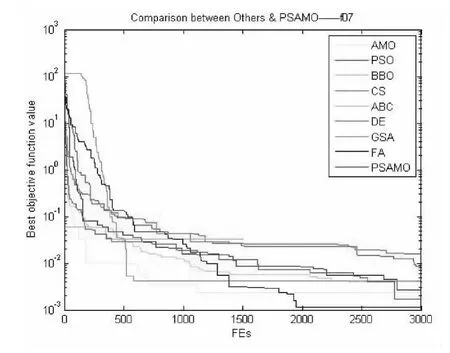
图9 对于f07函数PSAMO和其他算法性能的比较

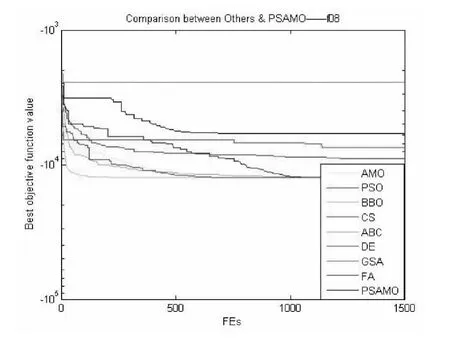
图10 对于f08函数PSAMO和其他算法性能的比较

4.2 多峰高维函数

对于函数f08到f13，最终解是非常重要的，因为函数能反应出来算法跳出局部极小和获得全局最优的能力。我们测试了f08－f13，局部极小的数量以指数方式增长像函数增长的维度。通过表中可以看出最终解的平均值的排名，动物迁徙算法在最终解的排名上表现的十分优秀，我们也能发现在f8－f13的7个函数的平均排名里也是最好的。

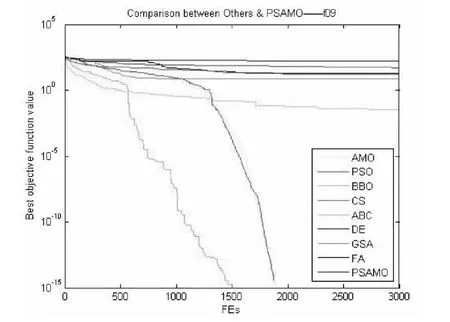
图11 对于f09函数PSAMO和其他算法性能的比较

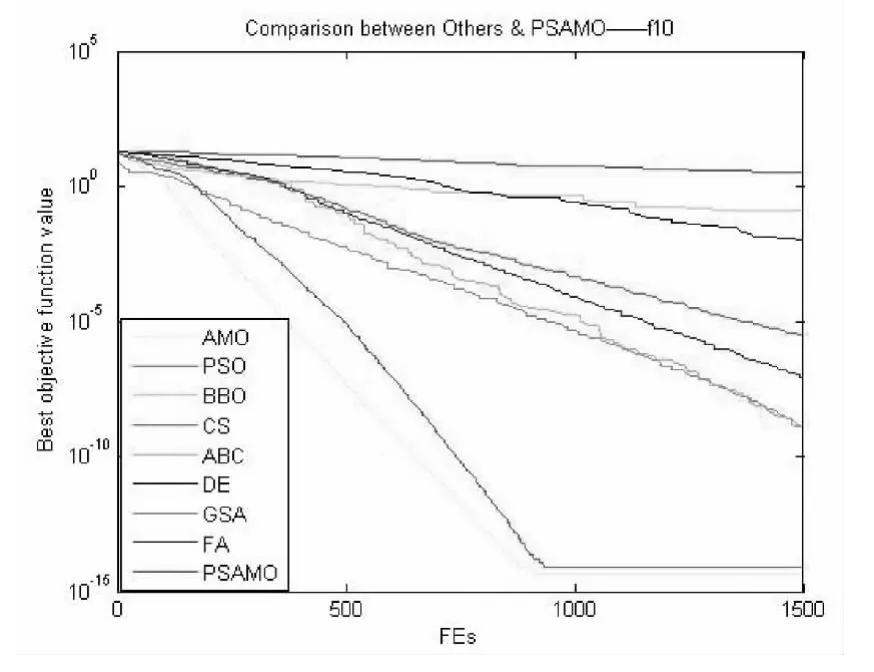
图12 对于f10函数PSAMO和其他算法性能的比较

通过对图10，图11，图12的研究可以看出，在多峰高维函数优化中，取得最优解的值是非常重要的。其中PSAMO在求解高峰多维函数时，表现良好。

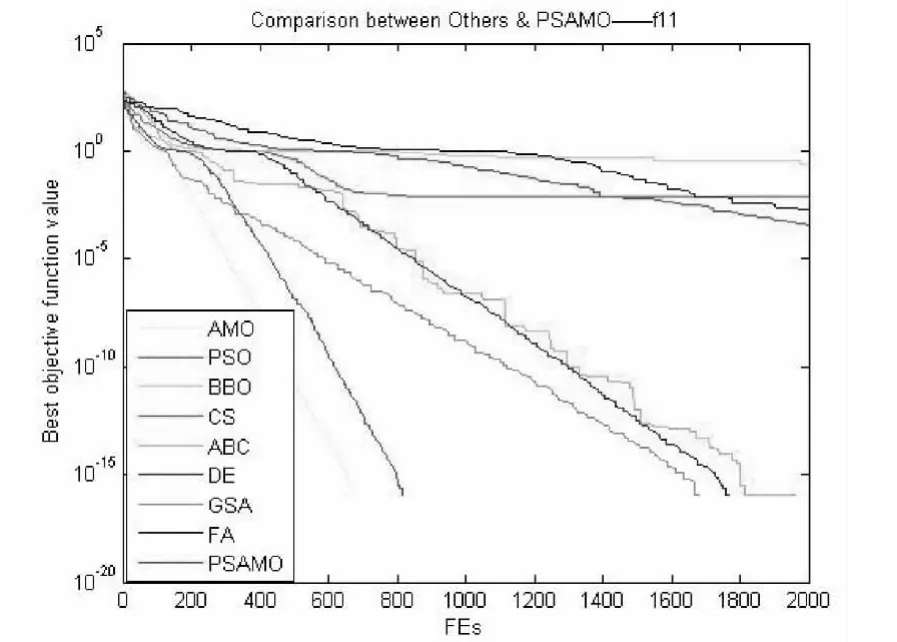
图13 对于f11函数PSAMO和其他算法性能的比较

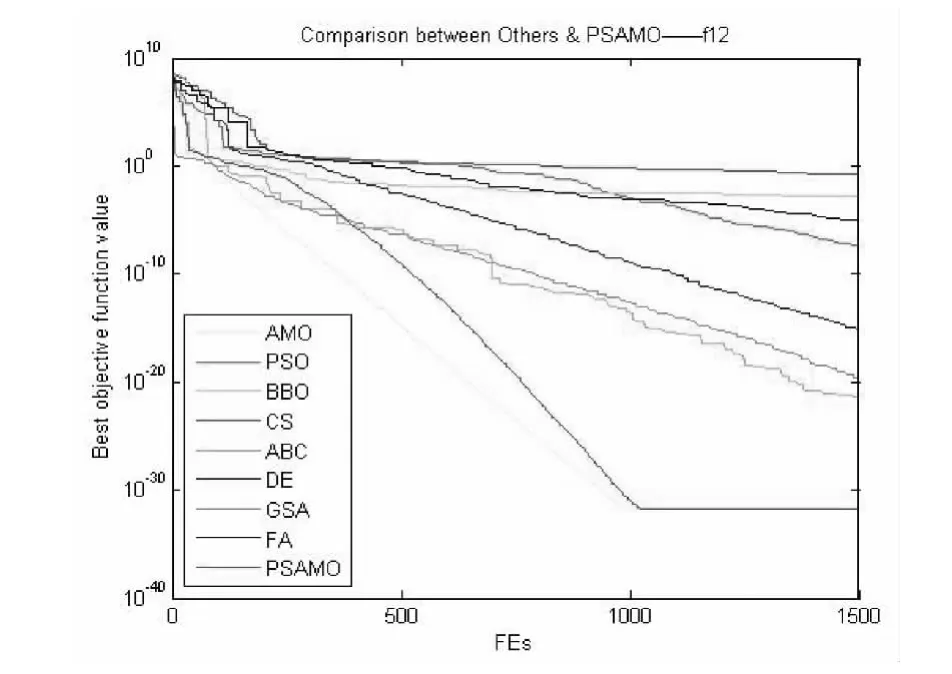
图14 对于f12函数PSAMO和其他算法性能的比较

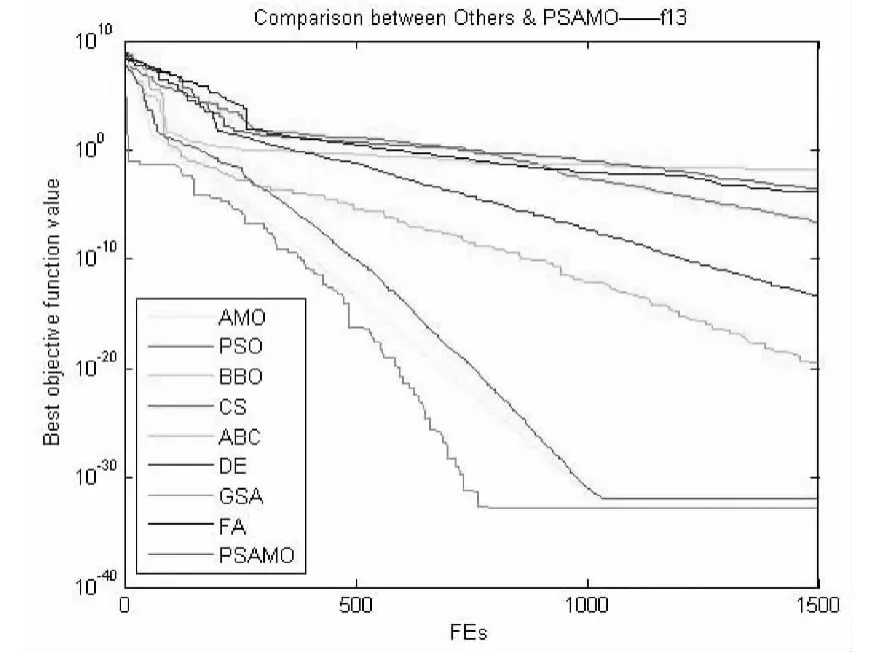
图15 对于f13函数PSAMO和其他算法性能的比较

通过观察图13，图14，图15可以发现，在求解多峰高维函数时，传统算法所得到的最优解不如混合动物迁徙算法所得到的最优解好。

4.3 多峰低维函数

对于函数f14－f23，f14－f23是比f08－f13更简单的多峰低维函数。对于f14－f23这10个函数来说，混合算法都表现十分良好，不仅单个函数排名是最好的，而且平均排名也是最好的。

5 结语

本文提出了一种改进的动物迁徙算法，将动物迁徙算法中全局搜索部分改为使用标准粒子群优化算法，用以提高动物迁徙算法的全局搜索能力还有其收敛速率。实验结果表明，改进后的动物迁徙算法在求解23个benchmark基准测试函数时，性能有了明显提高，体现了算法的有效性。

这一改进的动物迁徙算法目前只应用于求解连续的全局优化问题上，目前也有不少学者正在进行离散空间求解的研究。如何将混合动物迁徙算法应用在全新的领域，如多目标优化问题、约束优化问题、动态优化问题等，需要进一步的分析研究。

［1］Li X，Zhang J，Yin M.Animal migration optimization:an optimization algorithm inspired by animal migration behavior［J］.Neural Computing and Applications，2014，24(7):1867－1877.

［2］Cao Y，Li X，Wang J.Opposition－based Animal Migration Optimization［J］.Mathematical Problem.

［3］J.Kennedy，and R.C.Eberhart .Particle swarm optimization［C］//.In Proceedings of the 1995 IEEE International Conference on Neural Networks，volume 4 pages 1942－1948 IEEE Press ，Piscataway ，NJ ，1995 in Engineering 2013，2013(1):1－7.

［4］Yang XS.Nature－inspired Metaheuristic Algorithms［M］.Frome:Luniver Press，2008.

［5］Yang XS，Deb S.Cuckoo search via Levy flights［C］.Nature＆ Biologically inspired computing.World Congress on IEEE，2009:210－214.