Will oscillating wave surge converters survive tsunamis？

L.O’Brien，P.Christodoulides，E.Renzi，T.Stefnkis，F.Dis，∗

aSchool of Mathematical Sciences，Monash University，Victoria 3800，Australia

bFaculty of Engineering and Technology，Cyprus University of Technology，Limassol，Cyprus

cSchool of Mathematical Sciences，University College Dublin，Belfield Dublin 4，Ireland

dDepartment of Mathematical Sciences，Loughborough University，Loughborough，Leics LE11 3TU，UK

eCentre de Mathématiques et de Leurs Applications（CMLA），Ecole Normale Supérieure de Cachan，94235 Cachan，France

Will oscillating wave surge converters survive tsunamis？

L.O’Briena，P.Christodoulidesb，E.Renzic，d，T.Stefanakisc，e，F.Diasc，e，∗

aSchool of Mathematical Sciences，Monash University，Victoria 3800，Australia

bFaculty of Engineering and Technology，Cyprus University of Technology，Limassol，Cyprus

cSchool of Mathematical Sciences，University College Dublin，Belfield Dublin 4，Ireland

dDepartment of Mathematical Sciences，Loughborough University，Loughborough，Leics LE11 3TU，UK

eCentre de Mathématiques et de Leurs Applications（CMLA），Ecole Normale Supérieure de Cachan，94235 Cachan，France

A R T I C L E I N F O

Article history:

8 May 2015

Accepted 14 May 2015

Available online 9 June 2015

Tsunami

Wave energy converter

Wave loading

Oscillating wave surge converter

Wave-structure interaction

With an increasing emphasis on renewable energy resources，wave power technology is becoming one of the realistic solutions.However，the 2011 tsunami in Japan was a harsh reminder of the ferocity of the ocean.Itisknownthattsunamisarenearlyundetectableintheopenoceanbutasthewaveapproachesthe shore its energy is compressed，creating large destructive waves.The question posed here is whether an oscillating wave surge converter（OWSC）could withstand the force of an incoming tsunami.Several tools are used to provide an answer:an analytical 3D model developed within the framework of linear theory，a numerical model based on the non-linear shallow water equations and empirical formulas.Numerical resultsshowthatrun-upanddraw-downcanbeamplifiedundersomecircumstances，leadingtoanOWSC lying on dry ground！

©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY license（http://creativecommons.org/licenses/by/4.0/）.

1.Introduction

The estimation of the effects of tsunami-induced loading on near-shoreline structures located within inundation zones has recently gained significant interest from researchers，engineers，and government agencies［1，2］.Wave energy devices and tidal current turbines are slowly becoming a reality.Various prototypes are now being tested in harsh sea conditions，due for example to violent storms.The effectiveness of a mooring system to hold a turbine under extreme weather conditions has been examined for example by Chen and Lam［3］.Tiron et al.［4］provided a review on the challenges that wave energy devices face，in particular those associated with extreme wave events.What about tsunamis？

Therewasnowaveenergyconverter（WEC）installedatthetime oftheMarch11，2011Japantsunamibut thereissomeinformation available about offshore wind turbines.Simply structured windpower plants proved more resistant to natural disasters than nuclear plants.For example the wind plant 50 m off the coast of Kamisu，Ibaraki Prefecture，survived the massive tsunami and continues to run at full capacity supplying electricity to Tokyo Electric Power Co.，which was greatly compromised when the waves crippled the Fukushima No.1 nuclear plant.The wind plant has seven power generators.Each generator is attached to three propeller blades sitting atop a mast that，when turning，transform wind into electricity.Each mast，sunk into the seabed at a depth of 25 m，stands roughly 70 m above the water.The tsunami reached 5 m.Each transformer is located on a jetty dozens of meters away from the masts.The machine stayed dry amid the tsunami because the jetty，connected to a coastal road，is 9.6 m above sea level and the walls and ceiling kept water from splashing onto the machine.

Even if offshore wind turbines seem to have survived the 2011 Japan tsunami，it is legitimate to ask whether WECs will resist tsunamis.In the future some WECs could be installed in areas prone to tsunamis（off the coasts of Oregon or Washington for example where a devastating Cascadia earthquake could generate a threatening tsunami）.For the North Sea，the threat is not as obvious，even though O’Brien et al.［5］have indicated some possibilities for tsunamis.A large underwater landslide，called the Peach slide，took place on the Barra Fan，about 250 km off the North West coast of Ireland.It has a minimum age of 14680 years BP，was formed through a combination of blocky and muddy debris flows and affects an area of 700 km2.A landslide of such proportion could very well have generated a large scale tsunami.The Storegga slide is one of the world’s largest known submarine landslides and occurred off the west coast of Norway generating a hugetsunami.Recent studies estimate that the slide removed between 2500 km3and 3500 km3of sediment from the slide scar approximately 8200 years BP.It is thought that inundation was as high as 30 m and reached Norway，Shetland，Scotland，and the Faroes.For deep sea WECs，such as Pelamis［6］（Fig.1），or for current turbines usually installed at the sea bottom under at least 30 m of water，tsunamis are not anticipated to be a threat since they are located far from the shore（the present Pelamis prototype operating at EMEC［7］，Orkney，is located 1.6 km from the shore and the present OpenHydro［8］project in Brittany，France，is located 2 km from the shore）.Ontheotherhand，fornearshoreWECs，suchastheoscillating wave surge converter（OWSC）Oyster［9］（Fig.2），it is important to take a closer look at the effect of tsunamis（the present Oyster prototype operating at EMEC，Orkney，is located 500 m from the shore）.Unfortunately there is very few tsunami wave data away from the shoreline.One exception is the Mercator yacht，anchored 1.6 km away from the shore in Thailand during the 2004 Indian Ocean tsunami.The water depth was about 12-13 m and the yacht experienced four major waves，one‘‘depression’’wave（2.8 m）and three‘‘elevation’’waves（3.8，1.7，and 4.2）［10］.The problem of tsunami-induced loading is quite different from the problem of wave forces acting on flap-type storm surge barriers［11-13］because the periods involved are different.From the point of view of globalwaveloading，tsunamisarelessofathreatthanstormsurges orextremestormwavesasshownbelow.However，therearesome other issues，e.g.，extreme rundown，wave impact after the OWSC has been left on dry ground，wave breaking on the OWSC.

Fig.1.Photo of the Pelamis wave power device［6］.The device is typically 1600 m from the shoreline.

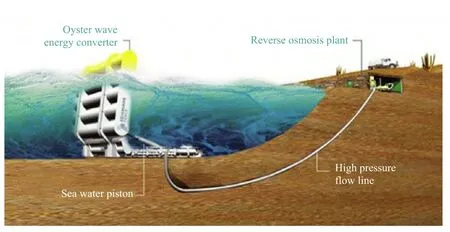
Fig.2.Drawing of the Oyster wave power device［9］.The water depth is between 10 m and 13 m where the device is installed.The device is typically 500 m from the shoreline.

St-Germain et al.［14］simulated the impact on structures of tsunami-like bores rapidly advancing on dry and wet beds.They used a 3D numerical model based on the smoothed particle hydrodynamics（SPH）method.The time-histories of the pressures and net force acting on a square column and a vertical wall due to the impact of these bores were compared qualitatively.To better understand the development of the hydrodynamic forces，a detailed analysis of the velocity field and of the water surface elevation was also incorporated.This study was part of a comprehensive interdisciplinary research program whose purpose was to help develop design guidelines for tsunami-prone structures.

Until recently there has been very little emphasis on drawdowns.For obvious reasons，residents care more about run-ups！With the development of OWSCs，the focus is different.It is in the vicinity of the extreme draw-down location that the maximum momentum flux occurs［15］.

For the methods，we use an analytical 3D model developed within the framework of linear theory by Renzi and Dias［16］，numerical solutions based on the non-linear shallow water equations［17］and empirical formulas［18，19］.

In Section 2，we briefly investigate the transformation of tsunamiwavesastheyapproachtheshore.InSection3，wepresent results based on an analytical model and we show that they do not allow us to conclude on the loading exerted by tsunamis.In Section 4，we discuss numerical results.In Section 5，we discuss the relevance of empirical formulas.

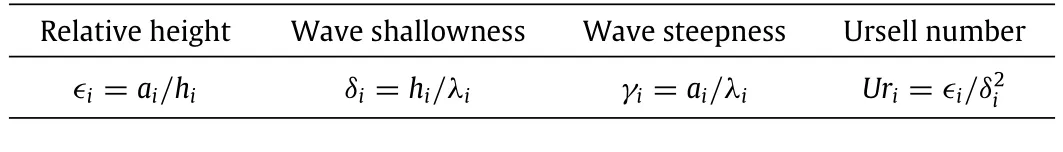
Table 1Dimensionless numbers.

2.Tsunami wave transformation

The wave transformation during the final stage of the propagation of a tsunami has been described in several papers.A particularly clear example is the paper of Madsen and Fuhrman［19］.Kajiura［20］considerstheamplificationoftsunamiswhichadvance towards shore over a gentle slope using Green’s law for tsunamis

whereaiandλiaretheamplitudeandwavelengthofatsunamiata depthhi，attwodifferentpositionsi=1，2.Moreinterestinginthe framework of the present study is the amplification of velocity and consequently of the momentum flux per unit breadthSince uiscales asin linear shallow water theory

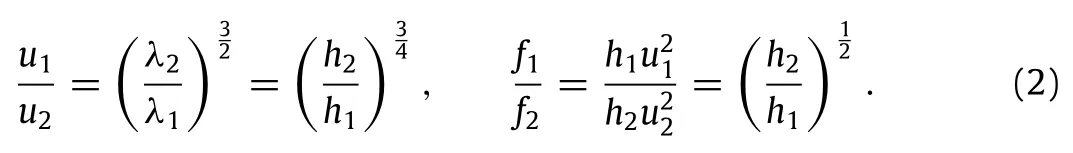
If the water depth is reduced by half between two points，the wave height increases by 19%while the momentum flux increases by 41%.As stated by Carrier et al.［15］，f can be interpreted as the drag force per unit breadth for a surface-piercing stationary object placed vertically over the flow depth.

In order to assess the importance of linear，non-linear and dispersive effects，four dimensionless parameters are defined in Table 1.

Eq.（1）implies that these dimensionless numbers are transformed as follows:

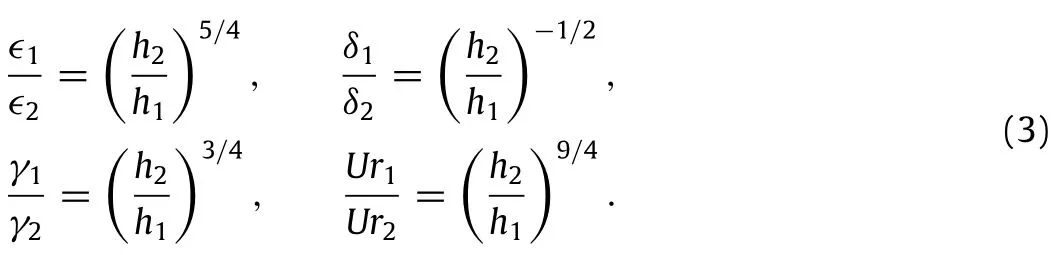
For a large tsunami wave with a1= 1 m，h1= 3 km，λ1=100 km，the transformation of the dimensionless parameters arising from Table 1 is shown in Table 2 for two depths:30 m and 10 m.

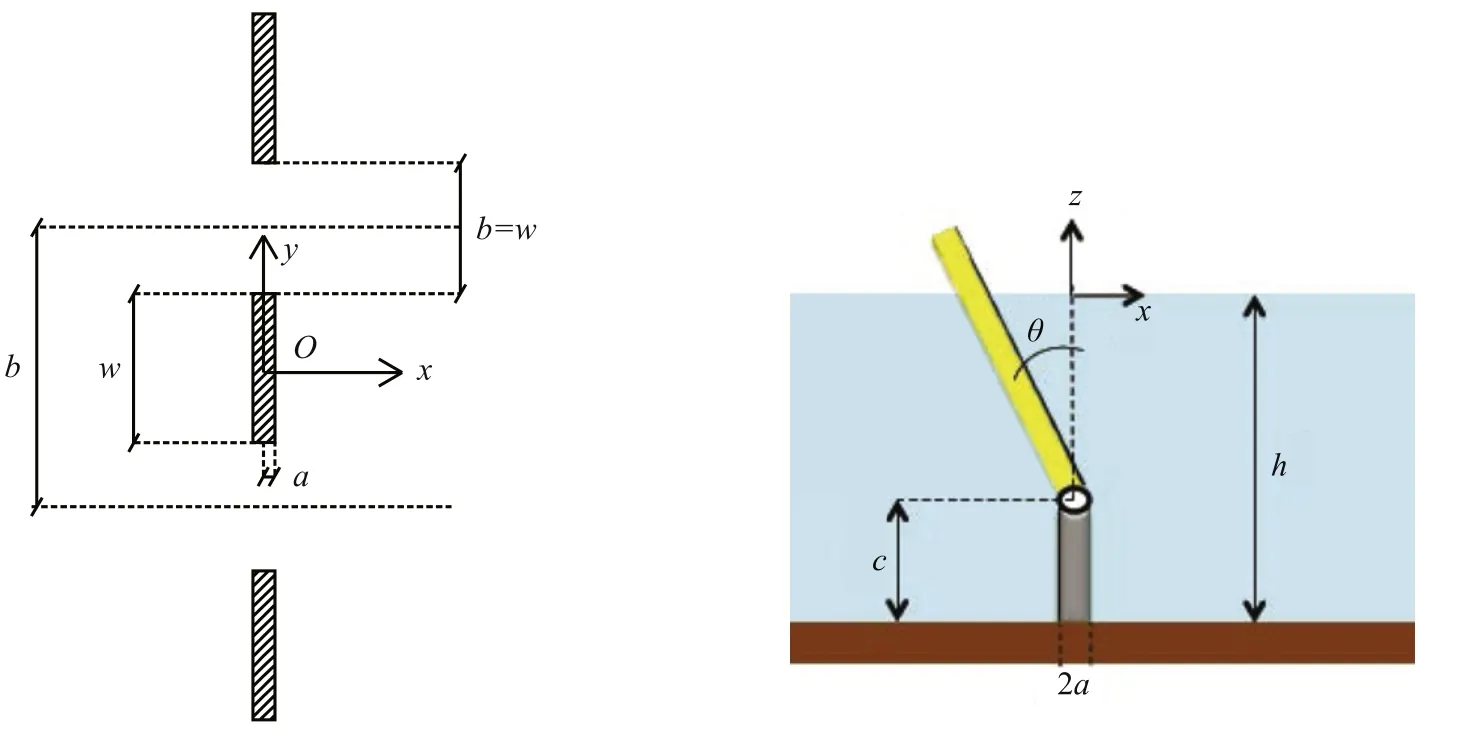
Fig.3.Geometry of the array of OWSCs:plan view（left）and side view（right）.

Table 2Transformation of dimensionless numbers for a tsunami at three positions according to Eq.（3）.

The values of relative heightϵindicate that linear theory can be used to describe the behavior of the wave up to a certain depth and the values of wave shallownessδsuggest that slight dispersive effects should be included for waves traveling over very large distances.As the wave approaches the shore，finite amplitude（nonlinear）effects come into play when the relative heightϵ≈10-1.According to Eq.（3）this occurs at a depth slightly larger than h=30 m.Assuming a seabed slope of 0.02 this occurs at a distance of approximately 1.5 km from the shore，which is about 1/7 ofthewavelengthofatsunamiwithaperiodof10min.Thedimensionless parameters corresponding to h=30 m are shown in column 2 of Table 2.The wave steepness isγ≈0.0003 and the Ursell number is Ur≈ 104≫ 1，indicating that dispersion is relatively minor compared with the non-linearity except for the front part of the wave.From these considerations，it is reasonable to conclude that at this distance from the shore there is a shift in importance from linear to non-linear effects.Therefore，linear shallow-water equations used offshore should be matched to the inner solution ofthenon-linearshallow-waterequationsatadistancefromshore of about 1/7 of a wavelength of the tsunami.At a depth of 10 m，the situation is even worse.The dimensionless parameters corresponding to h=10 m are shown in column 3 of Table 2.

Inthenextsection，lineartheoryisusedasafirstapproximation to predict the force exerted on an OWSC.It will be shown in Section 4 that as anticipated the linear results underestimate the force and that it is necessary to use non-linear theory.

3.Linear theory

We consider here the following idealized problem:a flap-type structure mounted on a flat sea bottom pierces the surface of the ocean.The structure is assumed to be fixed.The loading on the flap due to a tsunami wave is estimated.The most restrictive assumption is that the bottom is flat.

The analytical 3D model developed by Renzi and Dias［16］is used to compute the load on the flap.This is the same model that is implemented to determine the hydrodynamic loading on an array of OWSCs in random seas［21-23］.Until now，this model had only been used to compute forces under normal operational conditions for OWSCs，that is waves with periods between 5 s and 20 s.Even thoughthereisnoassumptiononthewaveperiodinthederivation of the model，special care must be taken when evaluating the solution for long waves.

Let us consider an infinite array of equally spaced thin plates in the open ocean used for the purpose of wave energy conversion.The analysis of the scattering problem，in which the flaps are held fixed in incoming waves，is used here to calculate the velocity potential and so，the pressure exerted on the system.This is important in order to investigate whether an array of nearshore OWSCs would survive the impact from a tsunami.Periodicity of the problem allows the geometry to be reduced to that of a single plate within two waveguides at a mutual distance b，as shown in Fig.3.

With reference to Fig.3，the plate is represented by a rectangular box of widthwand thickness 2a，fixed along a straight foundation at a distance c from the bottom of the ocean of depth h.The plate is in the middle of a channel of total width b.A plane reference system of coordinates x=（x，y，z）is also set，with x on the center line of the channel，y along the axis of the plate，and z positive upwards.Monochromatic waves of frequencyωare incoming from the left with wave crests parallel to the plate.

The theoretical basis of the mathematical model is provided by Renzi and Dias［16］and summarized here.Within the framework ofalinearpotential-flowtheory，thevelocitypotentialΦ（x，y，z，t）must satisfy the Laplace equation

in the fluid domain.On the free-surface，the kinematic-dynamic boundary condition

is applied，with g being the acceleration due to gravity.Absence of normal flux at the bottom and through the lateral walls of the channel requires

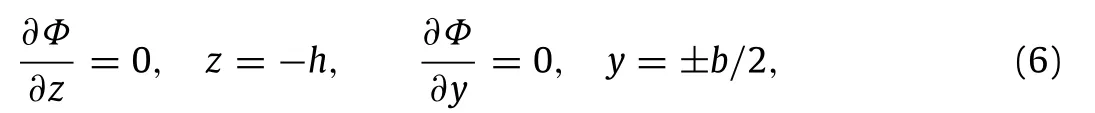
respectively.

A no-flux boundary condition must be applied on the lateral surfaces of the fixed plate，yielding

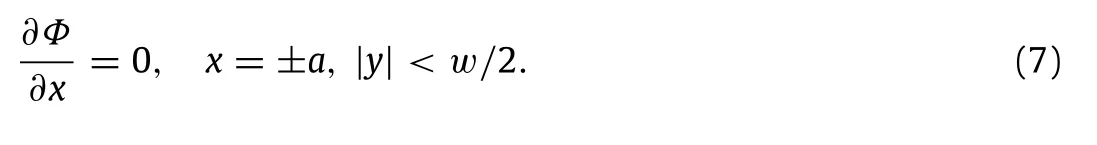
Since the total thickness of the plate 2a≪ b，the thin-plate approximation can be used［24］by which the boundary condition on the plate（7）is restated at x= ±0.Finally，the reflected and transmitted wave field respectively on the weather side and the lee side of the plate must be both outgoing at large distances from the origin.

The system of governing equations（4）-（7）can be solved via the introduction of a complex spatial potential such that

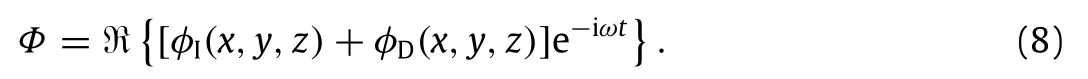
The velocity potential physically represents oscillating waves of period T=2π/ω，whose spatial variation is described by the sum of two different components，φIandφD.The first term，φI，represents the incident wave field and is given by

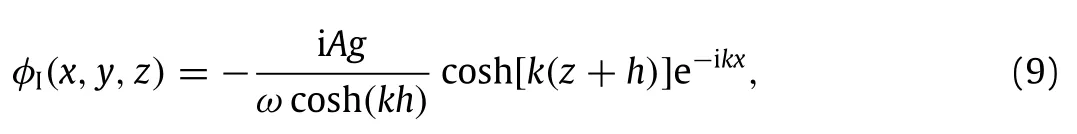
where A and k are respectively the wave amplitude and wavenumber，the latter depending on the wave frequency according to the dispersion relationω2=gktanh（kh）.

The full solution（for details see Refs.［16，25］）of（4）-（7）is based on a careful application of the Green integral theorem in the fluid domain.Herein we report the corresponding semianalytical solution and its physical meaning.Eq.（9）describes a monochromatic wave field.Incident monocromatic waves can describe the fundamental behavior of the flap.Referring to Eq.（8），φDis the diffraction potential that describes the modification of the wave field induced by the physical presence of the flap held fixed in water.The mathematical expression ofφD，not reported here for the sake of brevity，can be found in Ref.［25］.

The force of a tsunami on an array of nearshore OWSCs at a depth of 10.9 m is analyzed.If the tsunami has an amplitude of 1 m offshore at a depth of 3 km，then according to Green’s law for tsunamis（1）the amplitude of the wave will be approximately 4 m when it hits the devices.As said above，in order to analyze the tsunami effect on the system，we approximate the OWSCs as an array of fixed plates with a spatial period b=91.6 m and width w=18 m and determine the pressure exerted on one plate from a tsunamiwithamplitude4mandperiod10min.Inthelinearmodel p=-ρ（gz+Φt），the force exerted on the plate is determined by the pressure difference across the plate.We focus here on the dynamic pressure-ρΦt.The pressure jump across the plate is shown in Fig.4.It is plotted against y which runs along the axis of the plate and calculated at six equally spaced depths from the still waterleveltotheseafloor.Thegreatestoverallpressuredifference is felt at the center of the plate（y=0）and is zero at the edges of the plate（y=±9 m）but is invariant with depth.The maximum value isΔP≈3×103N/m2=0.03 bar.

In order to compare these results to a standard sea state，the pressure jump exerted by a typical swell with amplitude 3 m and period 5 s impacting on the plate is shown in Fig.5.This clearly shows how the pressure changes with depth:the maximum effect is felt at the free surface and the pressure decreases towards the sea floor.Also the magnitude is much greater than that from the tsunami，with a maximumΔP≈ 3×105N/m2=3 bar.From these results we can conclude that the tsunami load exerted on the plate does not vary with depth since it is such a long wave relative to the depth.Moreover，the magnitude of load exerted by the tsunami is approximately 100 times less than that of a normal swell.We can therefore assume that an array of nearshore OWSCs would easily withstand the force from a tsunami according to linear theory.However，as previously noted，non-linear effects will start to become important at approximately 1.5 km from the shore so non-linear effects on the plate will be investigated in the next section.

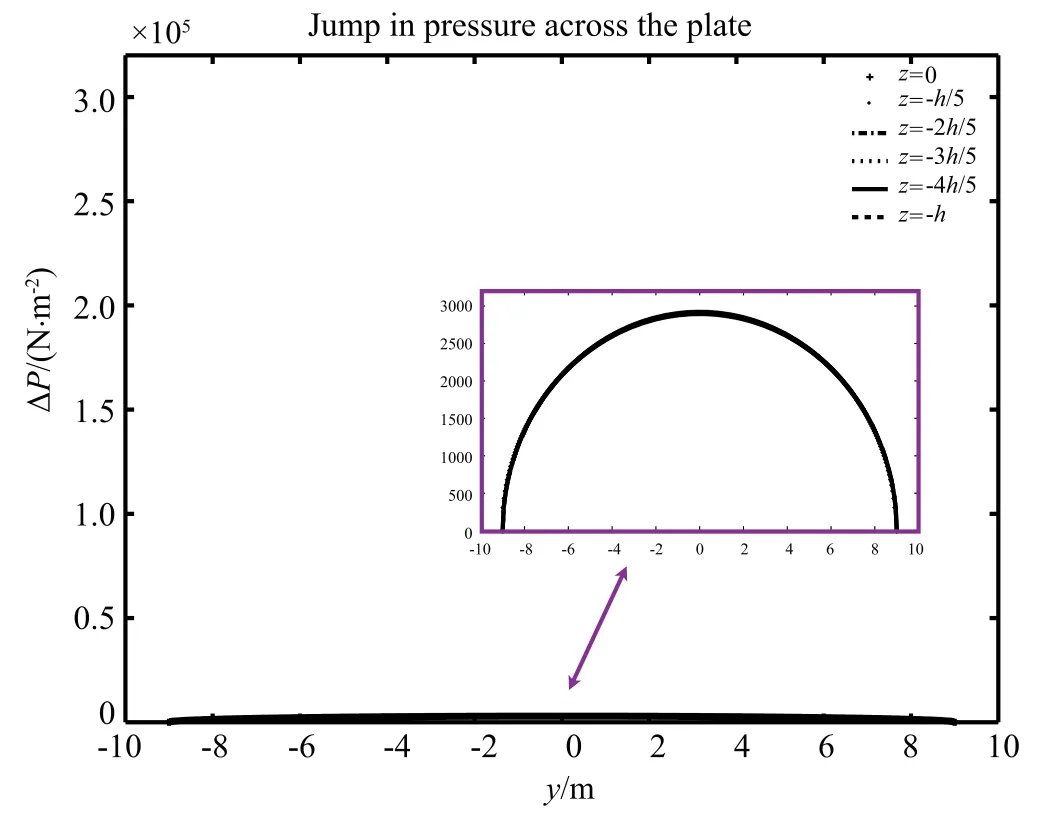
Fig.4.The jump in pressure for a typical tsunami across an 18 m plate，in a depth of h=10.9 m at six depths from the free surface to the ocean floor.

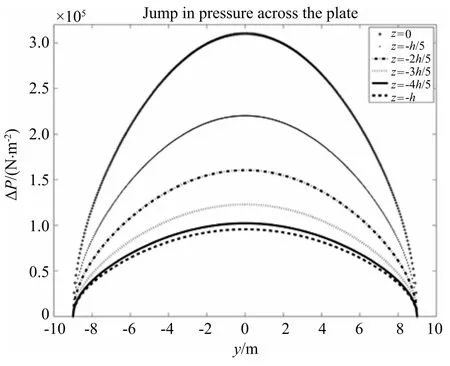
Fig.5.Variousjumpsinpressureacrossan18mplateforatypicalswell.（Thesame scales have been used in Figs.4 and 5.）

4.Beyond linear theory

The（1D）fully non-linear shallow water equations read

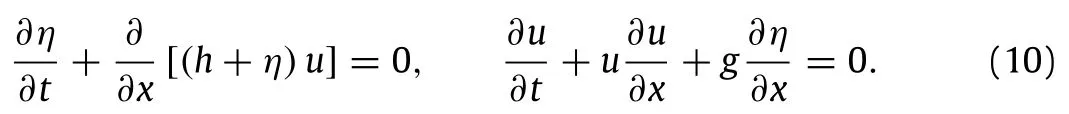
Consider a topography consisting of a sloping beach with unperturbed water depth varying linearly with the horizontal coordinate，h（x）= -αx.Carrier et al.［15］carefully evaluated tsunami run-up and draw-down motions on such a uniformly sloping beach.They considered several types of initial conditions.Kânoğlu［26］proposed an elegant alternative，which avoids the difficulty with the Carrier-Greenspan transformation，namely the derivation of an equivalent initial condition over the transform space for a given initial wave profile in the physical space.

Simply by looking at Ref.［15］，one can make some interesting comments:

One sees that a flap mounted in water depths of the order of 10 m will not become dry but it could be close（with a rundown of 8 m）.

It was shown in the previous section on linear theory that the forces due to the linear term∂Φ/∂t can be neglected.On the otherhand，the velocities can become quite large and the linearized approach can fail.A simple analysis provided by Madsen and Fuhrman［19］shows that maximum flow velocities of the order of 9 m/s canbereached.Consequentlythekineticenergycan be quite large.Since the pressure in the fully non-linear model includes a term proportional to u2，the forces can be quite large.Of course the bottom slope is an important parameter.A steep slope will provide smaller maximum flow velocities.

Carrier et al.［15］state that one of the drawbacks of their method is that it is only applicable for the problems in one spatial dimension with a uniformly sloping beach.Therefore we also used a two dimensionalnon-linearshallowwatersolver，VOLNA［27］，to perform additional simulations.If after the first wave recedes the device is left on dry land，a second wave may act as a shock on the plate and do more damage than it would to a partially submerged device.This effect is demonstrated in Fig.6.

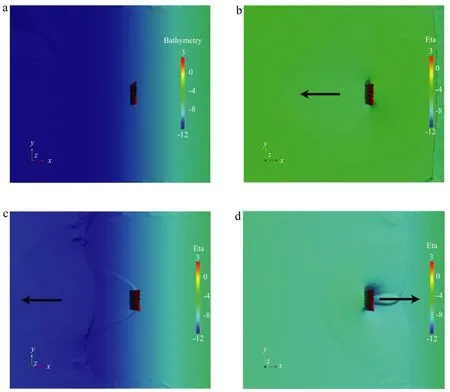
Fig.6.VOLNA simulation from multiple tsunami waves hitting a 13 m high plate in an initial depth of 10 m on a sea bed with slope 0.03（plane view）.（a）Bathymetry of a fixed plate on a sloping sea bed with the shore to the right of the plate.（b）The free surfaceηafter a tsunami has inundated the shore and it begins to recede.（c）45 s later，the plate is left on dry land.（d）Another 45 s later，a subsequent wave impacts the plate.

5.Empirical formulas

Authorities tend to classify the different forces acting on a structure due to a tsunami in the following way［28-32］:

•Hydrostatic Forces:Occur when standing or slowly moving water encounters a structure.They are caused by an imbalance of pressure due to a differential water depth on opposite sides of structure and act perpendicular to the surface.

•BuoyancyForces:Concernstructureswithlittleresistancetolift such as light wood frame buildings，basements，or swimming pools.These act vertically through the center of mass of the displaced volume.

•Hydrodynamic Forces:Caused by water flowing at a moderate to high velocity around a structure.These are a combination of thelateralforcescausedbythepressureforcesfromthemoving mass of water and the friction forces generated as the water flows around the structure.They include frontal impact，drag along the sides，and suction on the downstream side.These forces depend on flow velocity，fluid density，and structural geometry.

•Surge Force:Another variety of hydrodynamic force caused by the leading edge of a surge of a tsunami impinging on a structure.

•Impact Force:Results from debris or any object transported by

floodwaters，striking against a structure.

Assuming that the load is mainly hydrodynamic，even within thisidealizedframeworkitisnotclearwhatthemainforceisgoing to be.The loading for a solid wall facing the shoreline suggested by Yeh et al.［28］（ignoring impact forces and breaking wave forces）is given by the surge force

or the hydrodynamic force

whereρis the water density，g is the acceleration due to gravity，wis the width of the wall，A is the area of the wall，h is the surge height，Cd≈ 1.5 is the drag coefficient，andis the design flood velocity.

A comparison of the above empirical formulas for a plate of width 18 m and a surge of height 10 m gives Fs=8.1×107N and Fd=5.4×107N.Both values are of the same order of magnitude and two order of magnitude larger than the force obtained with linear theory.

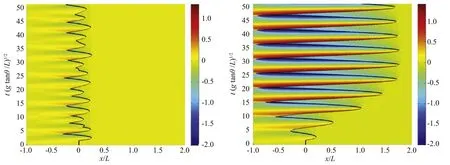
Fig.7.Non-resonant（left）and resonant（right）non-dimensional velocities from a monochromatic wave on a sloping beach with slope tanθ=0.13 and initial shoreline at x=0［35］.L is the distance from the shoreline to the point where the bottom becomes horizontal.

6.Conclusions

The hydrodynamic load of a tsunami on an array of nearshore OWSCs was investigated.The main conclusion is that non-linear theory must be used.Different forces suggested by standard tsunami design codes were reviewed displaying the variety of formulas and their reliance on estimated coefficients and a conservative velocity estimate.Applying the linear model of Renzi and Dias［16］to an array of fixed plates，a first approximation for the hydrodynamic loading on an OWSC was calculated through determining the jump in the-ρΦtterm.Results showed that the loadingforatypicaltsunamiisinvariantwithdepthandmaximum loading is felt at the center of the plate.By comparison with the loading from a typical swell，it was shown that the maximum net force of a tsunami on a nearshore OWSC is approximately one hundredth of the magnitude of the loading due to a regular sea state.This paradox arises because the linearized theory neglects high-orderhydrodynamicforces，whicharedominantinatsunami.However，further research needs to be done on the effects of multiple waves.Stefanakis et al.［33，34］demonstrated resonant phenomena between the incident wavelength and the beach slope withintheframeworkofthenon-linearshallowwaterequationsin onedimensionformultipletsunamiwaves.Acomparisonbetween the velocities of resonant and non-resonant states from Stefanakis et al.［35］is shown in Fig.7.Furthermore，if after the first wave recedes the device is left on dry land，a second wave may act as a shock on the plate and do more damage than it would to a partially submergeddevice.Webelievethatdangerousconfigurationscould be found with more detailed investigations.

Acknowledgments

The authors would like to acknowledge the support provided bytheScienceFoundationIreland（SFI）undertheprojectHigh-end computational modeling for wave energy systems，by the Framework Program for Research，Technological Development，and Innovation of the Cyprus Research Promotion Foundation under the Project AΣTI/0308（BE）/05，by the Irish Research Council for Science Engineering and Technology（IRCSET），by Aquamarine Power and by the European Union’s Seventh Framework Programme for research，technologicaldevelopmentanddemonstrationunderthe grant agreement ASTARTE No.603839.

References

［1］D.Palermo，I.Nistor，Y.Nouri，A.Cornett，Tsunami loading of nearshore structures:a primer，Can.J.Civil Eng.36（2009）1804-1815.http://dx.doi.org/10.1139/L09-104.

［2］Y.Nouri，I.Nistor，D.Palermo，A.Cornett，Experimental investigation of the tsunami impact on free standing structures，Coast.Eng.J.52（1）（2010）43-70.http://dx.doi.org/10.1142/S0578563410002117.

［3］L.Chen，W.-H.Lam，A review of survivability and remedial actions of tidal current turbines，Renew.Sustain.Energy Rev.43（2015）891-900.http://dx.doi.org/10.1016/j.rser.2014.11.071.

［4］R.Tiron，F.Mallon，F.Dias，E.G.Reynaud，The challenging life of wave energy devices at sea:A few points to consider，Renew.Sustain.Energy Rev.43（2015）1263-1272.http://dx.doi.org/10.1016/j.rser.2014.11.105.

［5］L.O’Brien，J.M.Dudley，F.Dias，Extreme wave events in Ireland:14 680 BP-2012，Nat.Hazards Earth Syst.Sci.13（3）（2013）625-648.http://dx.doi.org/10.5194/nhess-13-625-2013.URLhttp://www.nat-hazardsearth-syst-sci.net/13/625/2013/.

［6］Pelamis.www.pelamiswave.com，2015.

［7］EMEC.www.emec.org.uk，2015.

［8］OpenHydro.www.openhydro.com，2015.

［9］Aquamarine.www.aquamarinepower.com，2015.

［10］T.Rossetto，W.Allsop，I.Charvet，D.Robinson，Physical modelling of tsunami using a new pneumatic water wave generator，Coast.Eng.58（2011）517-527.http://dx.doi.org/10.1016/j.coastaleng.2011.01.012.

［11］P.Sammarco，H.H.Tran，C.C.Mei，Subharmonic resonance of Venice gates in waves.Part 1.Evolution equation and uniform incident waves，J.Fluid Mech.349（1997）295-325.http://dx.doi.org/10.1017/S0022112097006848.URL http://journals.cambridge.org/article_S0022112097006848.

［12］P.Sammarco，H.H.Tran，O.Gottlieb，C.C.Mei，SubharmonicresonanceofVenice gates in waves.Part 2.Sinusoidally modulated incident waves，J.Fluid Mech.349（1997）327-359.http://dx.doi.org/10.1017/S0022112097006836.URL http://journals.cambridge.org/article_S0022112097006836.

［13］T.Tomita，K.Shimosako，T.Takano，Wave forces acting on flap-type storm surge barrier and waves transmitted on it，in:Proc.13th Int.Offshore and Polar Engineering Conf.，Honolulu，Hawaii，USA，2003，pp.639-646.

［14］P.St-Germain，I.Nistor，R.Townsend，Numerical modeling of the impact with structures of tsunami bores propagating on dry and wet beds using the SPH method，Int.J.Protective Structures 3（2）（2012）221-255.http://dx.doi.org/10.1260/2041-4196.3.2.221.

［15］G.F.Carrier，T.T.Wu，H.Yeh，Tsunamirun-upanddraw-downonaplanebeach，J.Fluid Mech.475（2003）79-99.http://dx.doi.org/10.1017/S0022112002002653.

［16］E.Renzi，F.Dias，Resonant behaviour of the oscillating wave surge converter in a channel，J.Fluid Mech.701（2012）482-510.http://dx.doi.org/10.1017/jfm.2012.194.URL http://journals.cambridge.org/article_S0022112012001942.

［17］F.Dias，D.Dutykh，L.O’Brien，E.Renzi，T.Stefanakis，On the modelling of tsunami generation and tsunami inundation，in:Procedia IUTAM，vol.10，pp.338-355（2014）.http://dx.doi.org/10.1016/j.piutam.2014.01.029.

［18］L.O’Brien，P.Christodoulides，E.Renzi，D.Dutykh，F.Dias，The force of a Tsunami on a Wave Energy Converter，in:Proceedings of the Twenty-second International Offshore and Polar Engineering Conference，Rhodes，Greece，vol.1，June 17th-23rd（2012）.

［19］P.A.Madsen，D.R.Fuhrman，Run-up of tsunamis and long waves in terms of surf-similarity，Coast.Eng.55（2008）209-223.http://dx.doi.org/10.1016/j.coastaleng.2007.09.007.

［20］K.Kajiura，Local Behaviour of Tsunamis，in:D.Provis，R.Radok（Eds.），In Waves on Water of Variable Depth，in:Lecture Notes in Physics，vol.64，Springer-Verlag，Berlin，1977，pp.72-79.

［21］E.Renzi，L.O’Brien，F.Dias，Hydrodynamic loading on an array of oscillating wave surge converters in random seas.In:Proceedings of the Twenty-second International Offshore and Polar Engineering Conference，Rhodes，Greece，vol.1，pp.663-668，June 17th-23rd（2012）.

［22］D.Sarkar，E.Renzi，F.Dias，Wave power extraction by an oscillating wave surge converter in random seas，in:Proceedings of the 32nd International Conference on Ocean，Offshore and Arctic Engineering，Nantes，France，2013.

［23］D.Sarkar，E.Renzi，F.Dias，Wave farm modelling of oscillating wave surge converters，Proc.R.Soc.A 470（2014）20140118.http://dx.doi.org/10.1098/rspa.2014.0118.

［24］C.M.Linton，P.McIver，Mathematical Techniques for Wave/Structure Interactions，Chapman&Hall/CRC，2001.

［25］E.Renzi，F.Dias，Hydrodynamics of the oscillating wave surge converter in the open ocean，Eur.J.Mech.B Fluids 41（2013）1-10.http://dx.doi.org/10.1016/j.euromechflu.2013.01.007.

［26］U.Kânoğlu，Nonlinear evolution and runup-rundown of long waves over a sloping beach，J.Fluid Mech.513（2004）363-372.http://dx.doi.org/10.1017/S002211200400970X.ISSN 1469-7645.

［27］D.Dutykh，R.Poncet，F.Dias，The VOLNA code for the numerical modeling of tsunamiwaves:Generation，propagationandinundation，Eur.J.Mech.BFluids 30（6）（2011）598-615.http://dx.doi.org/10.1016/j.euromechflu.2011.05.005.

［28］H.Yeh，I.Robertson，J.Preuss，Development of Design Guidlines for Structures thatServeasTsunamiVerticalEvacuationSites，TechnicalReport，Washington Division of Geology and Earth Resources，November 2005.

［29］Federal Emergency Management Agency，FEMA Coastal Construction Manual，2000.

［30］ASCE Minimum Design Loads for Buildings and Other Structures，vol.ASCE 7-98，American Society of Civil Engineers，1998.

［31］City and County of Honolulu Building Code，Department of Planning and Permitting of Honolulu Hawaii，July 2000.

［32］Dames and Moore，Design and Construction Standards for Residential Construction in Tsunami-prone Areas in Hawaii.Dames&Moore，1980.

［33］T.Stefanakis，F.Dias，D.Dutykh，Local run-up amplification by resonant wave interactions，Phys.Rev.Lett.107（2011）.http://dx.doi.org/10.1103/PhysRevLett.107.124502.

［34］T.S.Stefanakis，S.Xu，D.Dutykh，F.Dias，Run-up amplification of transient long waves，Quart.Appl.Math.73（2015）177-199.http://dx.doi.org/10.1090/S0033-569X-2015-01377-0.

［35］T.S.Stefanakis，F.Dias，D.Dutykh，Resonant long-wave run-up on a plane beach，in:Proceedings of the Twenty-second International Offshore and Polar Engineering Conference，Rhodes，Greece，vol.3，June 17th-23rd（2012）.

11 January 2015

in revised form

∗at:School of Mathematical Sciences，University College Dublin，Belfield Dublin 4，Ireland.

E-mail address:laura.obrien@monash.edu（L.O’Brien）.

http://dx.doi.org/10.1016/j.taml.2015.05.008

2095-0349/©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY license（http://creativecommons.org/licenses/by/4.0/）.

*This article belongs to the Fluid Mechanics