Local buckling analysis of biological nanocomposites based on a beam-spring model

Zhiling Bai，Baohua Ji

Biomechanics and Biomaterials Laboratory，Department of Applied Mechanics，School of Aerospace Engineering，Beijing Institute of Technology，Beijing 100081，China

Local buckling analysis of biological nanocomposites based on a beam-spring model

Zhiling Bai，Baohua Ji∗

Biomechanics and Biomaterials Laboratory，Department of Applied Mechanics，School of Aerospace Engineering，Beijing Institute of Technology，Beijing 100081，China

A R T I C L E I N F O

Article history:

Accepted 12 May 2015

Available online 29 May 2015

Biological materials

Nanostructure

Staggered arrangement

Buckling behaviors

Aspect ratio

Composite materials

Biologicalmaterialssuchasbone，tooth，andnacreareload-bearingnanocompositescomposedofmineral and protein.Since the mineral crystals often have slender geometry，the nanocomposites are susceptible to buckle under the compressive load.In this paper，we analyze the local buckling behaviors of the nanocompositestructureofthebiologicalmaterialsusingabeam-springmodelbywhichwecanconsider plenty of mineral crystals and their interaction in our analysis compared with existing studies.We show that there is a transition of the buckling behaviors from a local buckling mode to a global one when we continuously increase the aspect ratio of mineral，leading to an increase of the buckling strength which levels off to the strength of the composites reinforced with continuous crystals.We find that the contact condition at the mineral tips has a striking effect on the local buckling mode at small aspect ratio，but the effect diminishes when the aspect ratio is large.Our analyses also show that the staggered arrangement of mineral plays a central role in the stability of the biological nanocomposites.

©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http://creativecommons.org/licenses/by-nc-nd/4.0/）.

Materials scientists have arrived at a consensus that biological nanocomposites，suchasbone，tooth，nacrehavesuperiormechanical properties due to the exquisite design of their microstructure fromnanotomacroscale［1-6］.Itwasshownthatthereisaconvergent nanocomposite structure consisting of mineral crystals and protein where the minerals often have large aspect ratio and staggered arrangement in the protein matrix［1，7-11］.A multitude of studies showed that this nanocomposite structure plays a central role in the mechanical properties from stiffness to strength and fracture toughness［12-17］，which provided valuable insights into the mechanical principles of the design of biological nanocomposites.

However，the mechanical behaviors of biological materials under compressive load have not yet been understood.Because the mineral crystals have high aspect ratio，and protein is up to three orders of magnitude softer than mineral，the nanocomposite structures are susceptible to buckle under compression.Therefore，it is interesting to ask the question how the biological materials deal with the possible buckling problem.Ji et al.［18］studied the buckling behaviors of a single mineral in the nanocomposites with the assumption that its neighboring minerals remain unbuckled，i.e.，the interaction between minerals are not considered， which leads to a higher buckling mode.Su et al.［19］studied the buckling behaviors of two neighboring minerals in a periodic unit by considering the coordination among the adjacent mineral crystals.The symmetric and anti-symmetric buckling modes were identified by using the perturbation method，and corresponding buckling strength for each mode was derived.They showed that the anti-symmetric mode often happens at small aspect ratio，but the symmetric mode at high aspect ratio，and their buckling strength both asymptotically approached to that of the continuous fiber reinforced composites predicted by the Rosen model［20，21］.

Those previous studies generally limited their analysis within a periodic unit，and the interaction among minerals beyond the unit is not considered.However，the buckling behaviors of composite structure at larger scale with many minerals should be much different.In this paper，we develop a simple beam-spring model，with which the buckling behaviors of a system with plenty of minerals can be analyzed，where the mineral is modeled by Euler beam while the matrix by distributed elastic spring.We focus on the effect of aspect ratio of minerals and the contact condition at the mineral tips on the buckling behaviors of the biocomposites.

It is arduous to analyze the buckling behaviors of the composite structure with many mineral crystals even using numerical method.An obstacle of such analysis is that massive elements must be used to discretize the mineral and protein system in order to get accurate buckling modes and strength using conventional2D or 3D elements，which，however，brings unfordable computing workload.In order to address this difficulty，here we introduce the beam-spring model，in which the mineral is modeled by Euler beam while the matrix is simplified by distributed elastic springs between minerals.Fig.1（a）depicts the model of the nanocomposite structure based on the beam-spring model.The mineral is arranged in a staggered manner，while the springs are arranged in a X-type pattern，as shown in Fig.1（b）and 1（c）.In addition，we consider two kinds of contact conditions between mineral tips along the longitudinal direction of mineral—one is no contact between the tips under the compressive load（Fig.1（b）），while the other is point contact between the tips（Fig.1（c））modeled by a pinned joint.There are up to 3640 minerals in the whole system.A homemade FORTRAN program is used to create nodes and elements and a MATLAB program to build the connection of springs with minerals and assemble the whole system，and then create the input file for ABAQUS program.In order to apply uniform compressive load，arigidplateisplacedateachloadingboundaryattheleftandright，while the top and bottom ones are maintained as straight lines by using the‘‘coupled degrees of freedom’’method（Fig.1（a））.

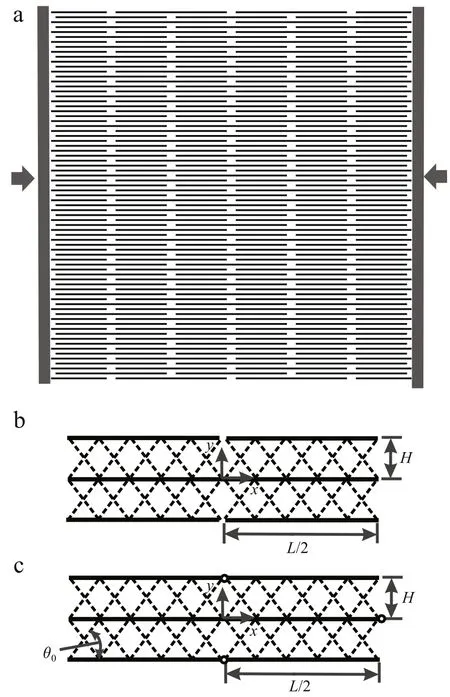
Fig.1.The beam-spring model of the nanocomposite structure of biological materials.（a）Finite element method（FEM）model of the nanocomposite in which themineralsarestaggeredintheproteinmatrix.Rigidbodyplatesareusedtoapply compressive loads at the left and right boundaries；（b）Free-staggered model of the periodic unit，where there is no contact at the mineral tips；（c）Pinned-staggered model of the periodic unit，where there is point contact at the mineral tips modeled by pinned joints.

The effective Young’s modulus EPand shear modulus GPof protein as function of spring constant K can be derived as（see the Supporting Materials（Appendix A）for detailed derivations），

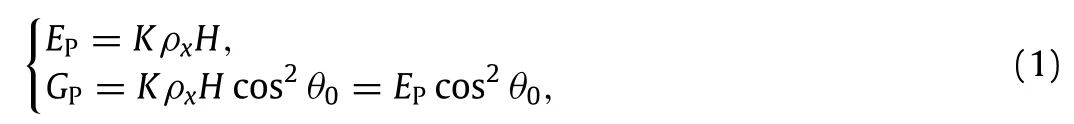
whereρxis the number density of springs along the beam length.Considering Poisson’s ratio of protein is almost equal to 0.5，we getθ0=54.7o（the angle between right slanting spring and the positive direction of x axis），and H=hPis the thickness of protein layer.

The effective Young’s modulus of the nanocomposite structure is then derived using the tension-shear chain model as［8，10］

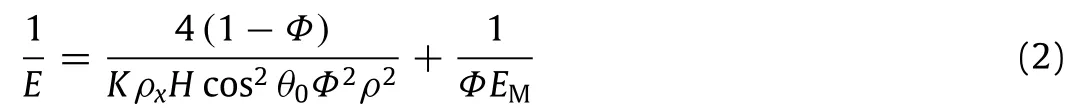
We first analyzed the buckling behaviors of the nanocomposite structure for the non-contact condition at the mineral tips（freestaggered model）at different aspect ratios of mineral.We found that the buckling mode was largely dependent on the aspect ratio，as shown in Fig.2.When the aspect ratio was small（i.e.，ρ=5），themineralcrystalswerepronetohaverigidbodyrotationwithout bending，whiletheproteinhadbothshearandtensile/compressive deformation.Note that the nanocomposite exhibited a typical local buckling mode with a periodic pattern along both horizontal and vertical direction；when the aspect ratio was increased to ρ =10，the mineral crystals then had both rigid body rotation and bending deformation，and protein undertook both shear and tensile deformation；if the aspect ratio was further increased to ρ =30，mineral crystal had more bending but less rigid body rotation，and protein undertook more shear deformation with slight lateral stretching at the end of minerals；finally，minerals undertook pure bending and protein had pure shearing when the aspect ratio was increased to as high asρ =50，at which the buckling mode approached to that of Rosen’s model，a global shear buckling mode［20］.

In the Rosen buckling mode，the continuous fibers undertake pure bending deformation，while soft matrix has pure shear deformation.The buckling strength of this buckling mode is given by Rosen’s model as［19］

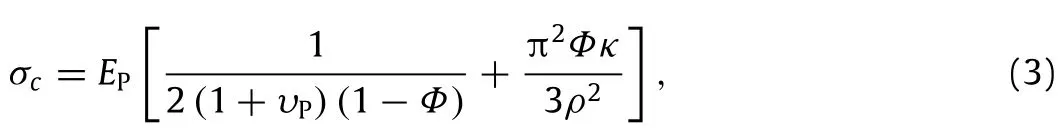
whereυPis Poisson’s ratio of protein，and.The critica l buckling strength predicted by the beam-spring model based FEM simulations is close to that of Eq.（3），which again validates the beam-spring model.

We then analyzed the buckling behaviors of the nanocomposites with point contact condition（pinned-staggered model）at different aspect ratios，as illustrated in Fig.3.We see that at the small aspectratio（ρ=5），thebucklingdeformationseverelylocalizedat theloadingboundariesanddegradedtowardsthecenterofthematerials，which is different from the behaviors of the free-staggered model.The mineral crystals near the loading boundary were prone to have rigid body rotation without bending，while the minerals away from the boundary hardly deformed；when the aspect ratio was increased toρ=10，the material started to exhibit a feature of global buckling，and the mineral crystals undertook both rigid body rotation and bending deformation，while protein had both shear and tensile deformation；when the aspect ratio was further increased toρ=30 and up，the buckling mode exhibited a pure shearing mode，approaching to that of Rosen’s model.

Our results showed that the aspect ratio of minerals plays a paramount role in the buckling behaviors of nanocomposite structure where the mineral are laid in a staggered manner inprotein matrix.Fig.4 depicts the normalized buckling strength of the nanocomposites as function of the aspect ratio for both freestaggered model and pinned-staggered model.We see that the bucklingstrengthcanbesignificantlyimprovedthroughincreasing the aspect ratio of minerals which finally levels off to that of Rosen’s model.The mechanism is that if the aspect ratio was small，the interaction between neighboring minerals was weak because small overlap among them，therefore the minerals were prone to independently rotate or deform，which causes the localization of buckling deformation in materials.But when the aspect ratio was increased，the buckling deformation exhibited a transition to a global manner through the coordination among neighboring minerals because the interaction among them was noticeably enhanced.Therefore，these results also imply that the staggered arrangement of mineral is crucial，which renders the buckling strength insensitive to the flaw at high aspect ratio despite of the flaw-like gap between the mineral tips，and thus approaches to that of the ideally continuous fiber reinforced composite，in consistency with previous studies［19，22］.For instance，Xie et al.［22］analyzed the buckling behaviors of stiff lamellae embedded in a compliant matrix under uniaxial compression，and they predicted sinusoidal buckling mode，which is similar to the global buckling configuration at large aspect ratio in this study.

Our results also showed that the contact conditions can influence the buckling behaviors，particularly at small aspect ratio of mineral.According to the comparison shown in Fig.4，when the aspect ratio was small，the strength of the free-staggered model was much lower than that of the pinned-staggered model，but the difference between the two models diminished when the aspect ratio became larger，at which both models asymptotically approached to that of Rosen’s model.Comparing Fig.2 with Fig.3，we see that the pattern of buckling modes of these two models are significantly different at small aspect ratio.Because the constraint at the pinned joints of minerals is stronger than that of the free ends，the strength of the pinned-staggered model is much larger than that of the free-staggered model at the small aspect ratio.In addition，the local buckling of the free-staggered model exhibited a periodic pattern at small aspect ratio，in stark contrast to that of the pinned-staggered model which was mostly localized at the loading boundary.When the aspect ratio was increased，the constraint from the lateral neighboring minerals rose up and became dominant as the overlap among the minerals increases，while the effect of constraint at the mineral tips became less important，therefore the difference between the two model became negligible at very large aspect ratio.

We showed that the wave length or the size of the periodic pattern of the buckling mode is larger than the periodic unit of nanocomposite structure，which are different from the buckling mode proposed by Su et al.［19］.In addition，the buckling mode in this study is neither pure symmetric mode nor anti-symmetric mode，as proposed by Su et al.This result demonstrates that a large system with many minerals is indispensable for fully understandingthebucklingbehaviorsofnanocompositesbywhich new buckling mode can be found.

Fig.2.Critical buckling modes of free-staggered model of the nanocomposites at different aspect ratios of minerals.

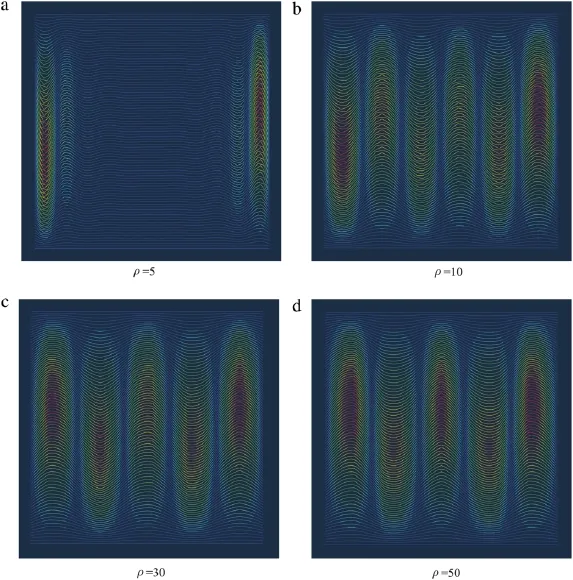
Fig.3.Critical buckling modes of pinned-staggered model of nanocomposites at different aspect ratios of minerals.

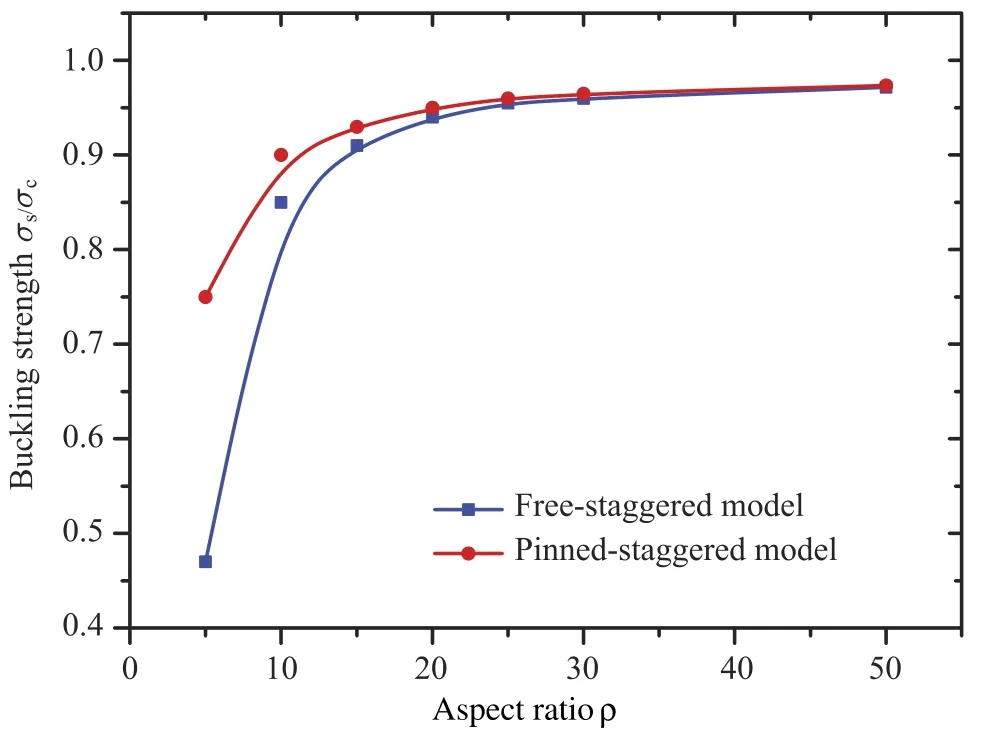
Fig.4.Normalizedbucklingstrengthofnanocompositestructureasfunctionofthe aspect ratio of mineral for two kinds of contact conditions at mineral tips.

Our predictions are consistent with prior experimental studies.For example，Menig et al.［3］carried out the quasi-static and dynamic compression on the abalone shells，and they found the micro-buckling in the layered structure of the shells.Because the aspect ratio of mineral in shells is around 10，which is comparably small，the buckling behaviors of the shells show a mixed feature of the buckling modes that we predicted in this study，i.e.，the local buckling mode（ρ＜10）and the global buckling mode（ρ＞10）.

In summary，our analysis showed that there is a buckling mode transition from local buckling to global one when the aspect ratio increases，which can significantly enhance the buckling strength.This result suggests that the aspect ratio takes a central role in the buckling properties of the nanocomposite structure，and the staggered arrangement is critically important in the load transfer anddeformationcoordinationamongtheminerals.Inaddition，the contact condition at the mineral tips also influences the buckling behaviors，especially at small aspect ratio.We demonstrated that the wave length or the size of buckling pattern is larger than that of the periodic unit of the nanocomposites，therefore these buckling modes are the lower ones than those found in previous studies.This work may shed more light on the buckling behaviors of biological nanocomposites and provides guidelines for biomimicking design of man made advanced materials.

Acknowledgment

This research was supported by the National Natural Science Foundation of China（11025208，11372042，and 11221202）.

Appendix.Supplementary data

Supplementary material related to this article can be found online at http://dx.doi.org/10.1016/j.taml.2015.05.006.

References

［1］H.D.Espinosa，J.E.Rim，F.Barthelat，M.J.Buehler，Merger of structure and material in nacre and bone—Perspectives on de novo biomimetic materials，Prog.Mater.Sci.54（2009）1059-1100.http://dx.doi.org/10.1016/j.pmatsci.2009.05.001.

［2］A.P.Jackson，J.F.V.Vincent，R.M.Turner，The mechanical design of nacre，Proc.R.Soc.London B 234（1988）415-440.

［3］R.Menig，M.H.Meyers，M.A.Meyers，K.S.Vecchio，Quasi-static and dynamic mechanical response of Haliotis rufescens（abalone）shells，Acta Materialia 48（2000）2383-2398.

［4］S.Kamat，X.Su，R.Ballarini，A.H.Heuer，Structural basis for the fracture toughness of the shell of the conch Strombus gigas，Nature 405（2000）1036-1040.http://dx.doi.org/10.1038/35016535.

［5］S.Weiner，A.Veis，E.Beniash，T.Arad，J.W.Dillon，B.Sabsay，F.Siddiqui，Peritubular dentin formation:Crystal organization and the macromolecular constituents in human teeth，J.Struct.Biol.126（1999）27-41.

［6］B.Ji，H.Gao，Mechanical principles of biological nanocomposites，Annu.Rev.Mater.Res.40（2010）77-100.http://dx.doi.org/10.1146/annurev-matsci-070909-104424.

［7］I.Jäger，P.Fratzl，Mineralized collagen fibrils:A mechanical model with a staggered arrangement of mineral particles，Biophys.J.79（2000）1737-1746.http://dx.doi.org/10.1016/S0006-3495（00）76426-5.

［8］H.Gao，B.Ji，I.L.Jager，E.Arzt，P.Fratzl，Materials become insensitive to flaws at nanoscale:Lessons from nature，Proc.Natl.Acad.Sci.USA 100（2003）5597-5600.http://dx.doi.org/10.1073/pnas.0631609100.

［9］H.Gao，B.Ji，M.J.Buehler，H.Yao，Flawtolerantbulkandsurfacenanostructures of biological systems，Mech.Chem.Biosyst.1（2004）37-52.

［10］B.Ji，H.Gao，Mechanical properties of nanostructure of biological materials，J.Mech.Phys.Solids 52（2004）1963-1990.http://dx.doi.org/10.1016/j.jmps.2004.03.006.

［11］B.Ji，H.Gao，A study of fracture mechanisms in biological nano-composites via the virtual internal bond model，Mater.Sci.Eng.A 366（2004）96-103.http://dx.doi.org/10.1016/j.msea.2003.08.121.

［12］F.Barthelat，R.Rabiei，Toughness amplification in natural composites，J.Mech.Phys.Solids 59（2011）829-840.http://dx.doi.org/10.1016/j.jmps.2011.01.001.

［13］Y.Shao，H.-P.Zhao，X.-Q.Feng，H.Gao，Discontinuous crack-bridging model for fracture toughness analysis of nacre，J.Mech.Phys.Solids 60（2012）1400-1419.http://dx.doi.org/10.1016/j.jmps.2012.04.011.

［14］F.Song，A.K.Soh，Y.L.Bai，Structural and mechanical properties of the organic matrix layers of nacre，Biomaterials 24（2003）3623-3631.http://dx.doi.org/10.1016/S0142-9612（03）00215-1.

［15］B.Bar-On，H.D.Wagner，Mechanicalmodelforstaggeredbio-structure，J.Mech.Phys.Solids 59（2011）1685-1701.http://dx.doi.org/10.1016/j.jmps.2011.06.005.

［16］G.Liu，B.Ji，K.-C.Hwang，B.C.Khoo，Analytical solutions of the displacement and stress fields of the nanocomposite structure of biological materials，Compos.Sci.Technol.71（2011）1190-1195.http://dx.doi.org/10.1016/j.compscitech.2011.03.011.

［17］B.Ji，H.Gao，Elastic properties of nanocomposite structure of bone，Compos.Sci.Technol.66（2006）1212-1218.http://dx.doi.org/10.1016/j.compscitech.2005.10.017.

［18］B.Ji，H.Gao，K.J.Hsia，How do slender mineral crystals resist buckling in biological materials？Phil.Mag.Lett.84（2004）631-641.http://dx.doi.org/10.1080/09500830512331329141.

［19］Y.Su，B.Ji，K.-C.Hwang，Y.Huang，Micro-buckling in the nanocomposite structure of biological materials，J.Mech.Phys.Solids 60（2012）1771-1790.http://dx.doi.org/10.1016/j.jmps.2012.05.003.

［20］B.W.Rosen，Mechanisms of Composite Strengthening，in:Fiber Composite Materials，American Society of Metals，1964.

［21］R.Parnes，A.Chiskis，Buckling of nano-fibre reinforced composites:a reexamination of elastic buckling，J.Mech.Phys.Solids 50（2002）855-879.

［22］W.-H.Xie，X.Huang，Y.-P.Cao，B.Li，X.-Q.Feng，Buckling and postbuckling of stiff lamellae in a compliant matrix，Compos.Sci.Technol.99（2014）89-95.http://dx.doi.org/10.1016/j.compscitech.2014.05.015.

13 January 2015

∗.Tel.:+86 10 68918309.E-mail address:bhji@bit.edu.cn（B.Ji）.

http://dx.doi.org/10.1016/j.taml.2015.05.006

2095-0349/©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http://creativecommons.org/licenses/by-nc-nd/4.0/）.

*This article belongs to the Solid Mechanics.