2D hierarchical lattices’imperfection sensitivity to missing bars defect

Bo Wng，Yunfeng Shi，∗，Rui Li，Youwei Chen，Yihu Mo

aState Key Laboratory of Structural Analysis for Industrial Equipment，Department of Engineering Mechanics，Dalian University of Technology，Dalian 116024，China

bBeijing Institute of Astronautical Systems Engineering，Beijing 100076，China

2D hierarchical lattices’imperfection sensitivity to missing bars defect

Bo Wanga，Yunfeng Shia，∗，Rui Lia，Youwei Chenb，Yihua Mob

aState Key Laboratory of Structural Analysis for Industrial Equipment，Department of Engineering Mechanics，Dalian University of Technology，Dalian 116024，China

bBeijing Institute of Astronautical Systems Engineering，Beijing 100076，China

A R T I C L E I N F O

Article history:

Accepted 5 November 2014

Available online 3 June 2015

Hierarchical structures

Lattices

Imperfection sensitivity

Elastic properties

Missing bars

Commercially available lattices contain various kinds of morphological imperfections which result in great degradation in lattices’mechanical properties，therefore，to obtain imperfection insensitive lattice structureisobviouslyapracticalresearchsubject.Hierarchicalstructurematerialswerefoundtobeaclass ofpromisinganti-defectmaterials.Thispaperbuildshierarchicallatticebyaddingsoftadhesiontolattice’s cell edges and numerical results show that its imperfection sensitivity to missing bars is minor compared with the classic lattice.Soft adhesion with appropriate properties reinforce cell edge’s bending stiffness and thus reduce the bending deformation in lattice caused by missing bars defect，which is confirmed by statisticalanalysisofnormalizednodedisplacementsofimperfectlatticesunderhydrostaticcompression and shear loads.

©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http://creativecommons.org/licenses/by-nc-nd/4.0/）.

Due to the high specific strength and specific moduli lattice materials have had a wide range of application in recent years［1-3］.However，commerciallyavailablelatticesalwayscontaindefects which result in degradation in lattices’mechanical properties［2-5］.Defects come in many different forms，among which the missing bars defect has the greatest influence on lattice’s behavior［4，5］.Anumberofresearcheshavebeencarriedoutonmechanicalpropertiesoflatticeswithmissingbarsdefect［4-6］.Hexagonal honeycomb is extremely sensitive to the presence of missing bars which causes a substantial knock down in the bulk modulus due to the induced bending stiffness of cell edge.It is found that with only 2%of missing cell edges a honeycomb’s bulk modulus will be reducedtoonehundredthofthatofaperfectone.Kagomelatticeis also sensitive to missing bars defect but the effect is not as strong as honeycomb while triangular lattice is not sensitive at all.The study［7］on the Kagome and triangular lattices single missing bar shows that the reduction in strength of Kagome lattice is greater than that of triangular lattice.Similar phenomenon is observed in 3D open cell foams that both Young’s modulus and bulk modulus are reduced by the presence of broken cell edges［8］.Other mechanical properties［6，9，10］such as platform stress and energy absorption of lattices have also been investigated and the results reveal that all properties are degraded at different levels due to missing bars defect.

Obviously there is a pressing need to find a method to strengthen lattices’resistance to missing bars defect since lattices show great sensitivity to this imperfection.Latest researches［11-14］suggest that hierarchical structures have excellent mechanical properties.Study on the mechanical properties of mature honeycomb［15］shows that mature honeycomb is stronger and stiffer than newborn honeycomb as the silk cocoons which cover the surfaces of cell edges grow thicker.Similarly，by attaching low-density foam material to the shell surface of a cylindrical shell shows an improvement in its yield strength［16-19］.There wereresearchersbuildinglatticematerialwithsandwichstructure cell edges and it turned out that both lattice’s mechanical properties and imperfection sensitivity were upgraded［20］.In general，hierarchical materials have the potential to be a class of promising anti-defects materials.

Inspired by the researches on hierarchical structures，this paper builds hierarchical lattice materials by adding soft adhesion to cell edges on the basis of hexagonal，Kagome and triangular lattices.Finite element models of imperfect lattices are established and emphasis is placed on numerically investigating the influence of adhesion on lattices’imperfection sensitivity and deformation modes.

Fig.1 shows three types of hierarchical lattices and the section ofcelledgewithadhesion.Threesectionparametersaredefinedasfollows in order to simplify the following contents:

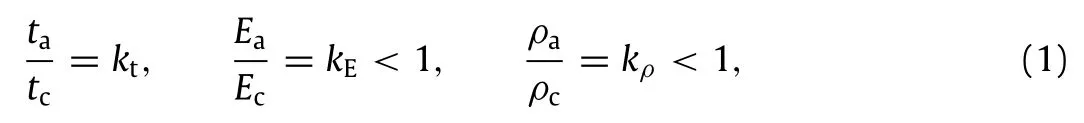
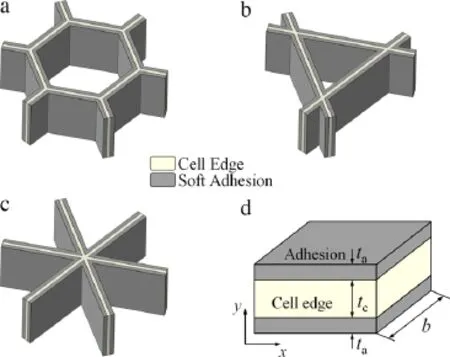
Fig.1.Hierarchical lattices and cell edge with adhesion.（a）Hierarchical hexagonal lattice.（b）HierarchicalKagomelattice.（c）Hierarchicaltriangularlattice.（d）Section of hierarchical lattice’s cell edge.

whereta，Eaandρaarerespectivelythethickness，Young’smodulus and density of adhesion layer，tc，Ecandρcare respectively the thickness，Young’s modulus and density of cell edge，as shown in Fig.1（d）.Meanwhile，the relative densityρof hierarchical lattices is defined as

whereρcandρaare the density of cell edge and adhesion layer，respectively，Vcand Vaare the corresponding volume.V is the overall volume of lattice.

Since the adhesion is much softer than lattice’s parent material，the equivalent stiffness of hierarchical lattice’s cell edge can be calculated on the basis of the Euler-Bernoulli beam theory.Hence the equivalent compressive stiffness（AE）∗and equivalent bending stiffness（EI）∗of cell edges with adhesion can be expressed as

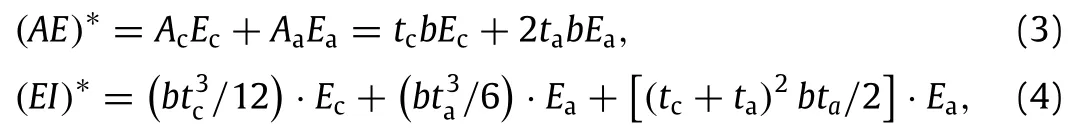
where Aaand Acare the section areas of adhesion layer and cell edge，while b is the out-plane thickness of lattice.

The ABAQUS/Standard version［21］was used here to establish the finite element models of imperfect hierarchical lattices，whereaB22Timoshenkobeamelement，whichcanbesubjectedto stretch，bendandshear，wasusedtorepresenteachcelledge［4，22］.Meshes of the imperfect hierarchical lattice were generated from perfect parent meshes using a MATLAB routine［23］，which randomlyremovedaproportionf oftheelements.Notethat f cantake valuesoftherangefrom0to0.1.Foragivenlevelofimperfectionf，the in-plane moduli were obtained by calculating the average bulk and shear moduli of twenty stochastic models with the same adhesion.The size of the lattice model was 48×48 unit cells which is large enough for the accuracy according to the study by Symons andFleck［5］.Thedisplacementsoflattices’boundarynodessatisfy the periodic boundary condition expressed as follows［4，5，22］

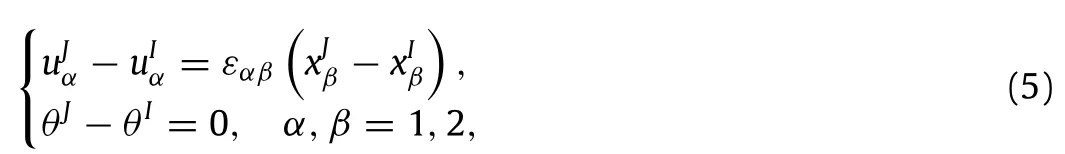
whereεαβis the representative volume element’s average micro strain，andare the coordinate values of the boundary nodes J and I before deformation,andare the linear displacements of J and I after deformation，andθJandθIare the angular displacements of J and I after deformation.

Since the adhesion layer is softer than the cell edge，the values of parameters kt，kEand kρshall be carefully decided.According to the former study［24］，six kinds of adhesion layers with different values of ktand kEwere performed to investigate the influence of adhesion’s mechanical and section properties on lattice’s in-plane moduli.Specifically，kttook values of 1 and 2 and kEtook values of 0.1，0.01 and 0.001 while the value of kρremained unchanged at 0.1.Noticethatforeachtypeoflatticestheirmasseswereconstants regardless of the values of ktand kEas the relative densities kρwere unchanged，which gave the precondition for the comparison between the hierarchical lattice and their corresponding classic lattice.

The value of t/l of perfect classic lattice was taken as 0.02［5］which indicated that the relative densities of hexagonal lattice，Kagome lattice and triangular lattice are respectively 0.023，0.035 and 0.069，where t and l were the thickness and length of perfect lattice’s cell edge，respectively.Numerical results of three types of hierarchical lattices with different adhesions under hydrostatic compression and shear loads are given as shown in Fig.2，where f was lattices’defect degree，K and G were the imperfect lattice’s bulk modulus and shear modulus respectively while K0and G0were the perfect lattice’s bulk modulus and shear modulus respectively.

According to Fig.2，hexagonal lattice’s bulk modulus and Kagome lattice’s bulk and shear moduli are sensitive to missing bars defect while hexagonal lattice’s shear modulus and triangular lattice’s bulk and shear moduli are insensitive.For those moduli which are imperfection sensitive，adding adhesion whose Young’s modulus are one tenth of that of cell edges makes significantly improvement on the moduli.However when adhesion’s Young’s modulusaredegradedtheimprovementturnedintoreduction.For those moduli which are imperfection insensitive，adding adhesion makes no differences whatever the adhesion’s properties are.

To analyze how adhesion influences hierarchical lattice’s imperfection sensitivity，the local deformation figures of lattices with a single edge missing are listed in Table 1.Note that all comparisons are based on the premise that lattices have the same relativedensity.Itcanbeseen that the missingbarsimperfection leads to lattice’s deformation mode switches from stretching dominated to bending dominated except for hexagonal lattice under shear load［5］.Hexagonal lattice under hydrostatic compression load is most affected，followed in order by Kagome lattice and triangular lattice under hydrostatic compression and shear loads.According toEq.（4），by addingadhesion ofpropertiesof0.1ρc-0.100Ec-2tcthe bending stiffness of hierarchical lattice’s cell edge is 4.88 times of that for the classic lattice’s cell edge，which indicates that the bending deformation caused by missing bars defect is weakened and thus the lattice becomes insensitive to the imperfection.In contrast，when the adhesion’s properties are 0.1ρc-0.001Ec-2tcthen the bending stiffness of hierarchical lattice’s cell edge becomes 0.41 times of that for the classic lattice’s cell edge，which indicates that the bending deformation is strengthened and the lattice becomes more sensitive to imperfection.In general，hierarchical lattice’s imperfection sensitivity is reduced if the adhesion upgrades the bending stiffness of cell edge while adhesion degrading the bending stiffness does the opposite.

To measure the influence of missing bars defect on hierarchical and classic lattices，statistical analysis was conducted for the normalized node displacement of classic lattices and hierarchical latticeswithadhesionofpropertiesof0.1Ec-0.1ρc-2tc，asshownin Table 1.Define lattice’s normalized node displacement∆/l as:

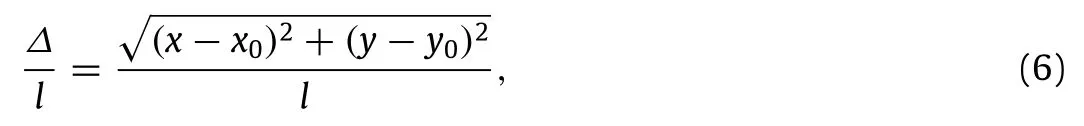
Fig.2.Imperfectsensitivitytomissingbarsdefectofhierarchicallatticesatgivenrelativedensity.（a）Hexagonallattice’sbulkmodulus.（b）Hexagonallattice’sshearmodulus.（c）Kagome lattice’s bulk modulus.（d）Kagome lattice’s shear modulus.（e）Triangular lattice’s bulk modulus.（f）Triangular lattice’s shear modulus.

Table 1

where（x，y）are the node coordinates of imperfect hierarchical or classic lattice with a certain bulk or shear strain while（x0，y0）are the node coordinates of corresponding perfect lattice with the samebulkorshearstrain；listhecelllength.Thestatisticalintervalis taken as 0.01 and then the probability of occurrence of nodes at each interval is calculated.It is obvious that lattice shows less imperfection sensitivity with a smaller mean and standard deviation of normalized node displacement.The results are shown in Fig.3.Note that the bulk or shear strains of all lattices are taken as 0.0208 and the results of Kagome and triangular lattices under shear load can be replaced by the results under hydrostatic compression load since these two lattices have the same deformation modes under both loads［5］，hence the former will not be shown.

According to Fig.3，for classic hexagonal and Kagome lattice under hydrostatic compression load，their normalized node displacement is uniformly distributed in every interval within a large range from 0 to 0.25，which reveals that nodes in imperfect classic lattice are seriously displaced from their ideal places as they were in perfect classic lattice，thus the missing bars defect has greatly affected classic lattice’s deformation mode.In contrast，the normalized node displacement of hierarchical hexagonal lattice under shear load and hierarchical triangular lattice under hydrostatic compression load are mostly concentrated in a small range of 0-0.1，which reveals most nodes in hierarchical lattice are closely around their ideal places and the missing bars defect has little influence on hierarchical lattice.The above conclusion can also be drawn from the fact that the mean and standard deviation of hierarchical lattice’s normalized node displacement are much smaller than that of classic lattice.

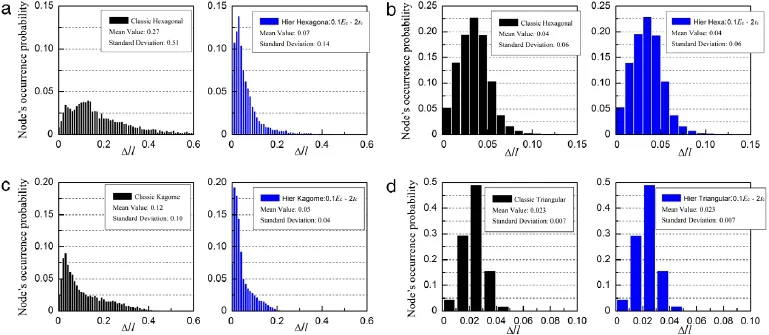
Fig.3.Probability of occurrence of normalized node displacement.（a）Hexagonal lattice with bulk strain of 0.0208 and f of 0.0001.（b）Hexagonal lattice with shear strain of 0.0208 and f of 0.05.（c）Kagome lattice with bulk strain of 0.0208 and f of 0.005.（d）Triangular lattice with bulk strain of 0.0208 and f of 0.05.

Since adhesion strengthens hierarchical lattice’s resistance to missing bars defect by increasing its cell edge’s bending stiffness and then weakens the bending deformation caused by defect，it is important to explore the dependence of lattice’s deformationmodeondefectdegree.Therebytherelativemoduliof hierarchical lattice are plotted against imperfect level f，as shown in Fig.4，where Khand Ghrepresent the bulk and shear moduli of hierarchical lattice while Kcand Gcrepresent the bulk and shear moduli of classic lattice.Note again that the results of Kagome and triangular lattices’shear moduli are neglected since they can be replaced by the results of bulk moduli.

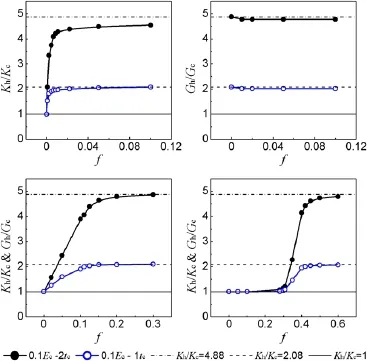
Fig.4.Hierarchical lattice’s relative moduli against imperfect degree f.（a）Hexagonal lattice’s relative bulk modulus.（b）Hexagonal lattice’s relative shear modulus.（c）Kagomelattice’srelativebulkandshearmoduli.（d）Triangularlattice’s relative bulk and shear moduli.

By adding adhesion of properties of 0.1Ec-0.1ρc-2tcand 0.1Ec-0.1ρc-tc，the bending stiffness of hierarchical lattice’s cell edge is respectively 4.88 and 2.08 times of that of classic lattice’s cell edge，while the compressive stiffness remains unchanged accordingtoEqs.（3）and（4）.Theoretically，ifthedefectdegreeislarge enough that lattices are completely bending dominated，and then

the values of Kh/Kccould reach 4.88 and 2.08 for lattices under hydrostatic compression load with adhesion of properties of 0.1Ec-0.1ρc-2tcand 0.1Ec-0.1ρc-tc，which is confirmed by Fig.4.In addition，the values of Kh/Kcof perfect lattices are 1 as both hierarchical and classic lattices under hydrostatic compression load are stretching dominated and their cell edges have the same compressive stiffness.As for hexagonal lattice under shear load with adhesion of properties of 0.1Ec-0.1ρc-2tcand 0.1Ec-0.1ρc-tc，thevaluesofGh/Gcremain4.88and2.08becauseitisbendinggovernedforbothperfectandimperfectlattices，whichmeansthatthe shear modulus of imperfect hierarchical lattice is greatly upgraded compared with that of perfect classic lattice.

From Fig.4 it can be seen that the bulk moduli of hexagonal and Kagome lattices are extremely sensitive to missing bars defect and their deformation modes start to switch from stretchingdominated to bending dominated as soon as the missing bars defect appears and so does the shear modulus of Kagome lattice.The bulk and shear moduli of triangular lattice are not affected by small degree of missing bars defect and their deformation modes start to switch from stretching dominated to bending dominated only after the value of f reaches 0.3.

Since commercially available lattices always contain defects which result in the degrading in lattice’s mechanical properties，to obtainimperfectioninsensitivelatticesstructureisimportant.This paper tries to build hierarchical lattices by adding soft adhesion layer to cell edges to degrade lattices’imperfection sensitivity.Three types of lattices（hexagonal，Kagome，and triangular lattices）were studied.The results indicate that by adding adhesion of properties of 0.1Ec-0.1ρc-2tcthe hierarchical lattices show a low level of imperfection sensitivity to missing bars defect.The degradation on the imperfection sensitivity of hexagonal lattice’s bulkmodulusisthegreatest，followedbyKagomelattice’sbulkand shear moduli.The degradations on the imperfection sensitivities of triangular lattice’s bulk and shear moduli can only be observed when the defect degree is incredibly large.In addition，though hexagonal lattice’s shear modulus is insensitive to missing bars defect，it is significantly improved by adding adhesion to the cell edges.The mechanism of adhesion strengthens lattices’resistance to missing bars defect is upgrading cell edge’s bending stiffness as the missing bars defect leads lattices’deformation modes switching from stretching dominated to bending dominated.

Acknowledgments

The research issupported by the 973 Program （No.2014CB049000，2011CB610304），NationalNaturalScienceFoundation of China（11372062，91216201），LNET Program（LJQ2013005），China Postdoctoral Science Foundation（2014M551070），111 Project（B14013）.

References

［1］L.J.Gibson，M.F.Ashby，Cellular Solids:Structure and Properties，Cambridge university press，1997.

［2］T.J.Lu，D.P.He，C.Q.Chen，C.Y.Zhao，D.N.Fang，X.L.Wang，The multifunctionality of ultra-light porous metals and their applications，Adv.Mech.4（2006）517-535.http://dx.doi.org/10.3321/j.issn:1000-0992.2006.04.004.

［3］B.Wang，B.Wang，G.Cheng，Multifunctional design of sandwich panels with Kagome-like cores，Fuhe Cailiao Xuebao，Acta Mater.Compos.Sin.3（2007）109-115.http://dx.doi.org/10.3321/j.issn:1000-3851.2007.03.020.

［4］C.Chen，T.Lu，N.Fleck，Effect of imperfections on the yielding of twodimensional foams，J.Mech.Phys.Solids 11（1999）2235-2272.

［5］D.D.Symons，N.A.Fleck，The imperfection sensitivity of isotropic twodimensional elastic lattices，J.Appl.Mech.5（2008）051001.http://dx.doi.org/10.1115/1.2913044.

［6］X.C.Zhang，Y.Liu，B.Wang，Z.-M.Zhang，Effects of defects on the inplane dynamic crushing of metal honeycombs，Int.J.Mech.Sci.10（2010）1290-1298.

［7］X.Cui，Y.Zhang，H.Zhao，T.J.Lu，D.Fang，Stress concentration in twodimensional lattices with imperfections，Acta Mech.1-4（2011）105-122.

［8］Y.Gan，C.Chen，Y.Shen，Three-dimensional modeling of the mechanical property of linearly elastic open cell foams，Int.J.Solids Struct.26（2005）6628-6642.

［9］X.C.Zhang，Y.Liu，Z.M.Zhang，Effects of concentrated defects on the in-plane dynamic properties of honeycombs，Eng.Mech.5（2011）239-244.

［10］A.Ajdari，H.Nayeb-Hashemi，A.Vaziri，Dynamic crushing and energy absorptionofregular，irregularandfunctionallygradedcellularstructures，Int.J.Solids Struct.3（2011）506-516.

［11］L.Zhao，Q.Zheng，H.Fan，F.Jin，Hierarchical composite honeycombs，Mater.Des.（2012）124-129.

［12］A.Vigliotti，D.Pasini，Mechanical properties of hierarchical lattices，Mech.Mater.（2013）32-43.

［13］J.W.Dunlop，P.Fratzl，Multilevel architectures in natural materials，Scr.Mater.1（2014）8-12.

［14］M.E.Kassner，S.Nemat-Nasser，Z.Suo，G.Bao，J.C.Barbour，L.C.Brinson，H.Espinosa，H.Gao，S.Granick，P.Gumbsch，New directions in mechanics，Mech.Mater.2（2005）231-259.

［15］K.Zhang，H.Duan，B.L.Karihaloo，J.Wang，Hierarchical，multilayered cell walls reinforced by recycled silk cocoons enhance the structural integrity of honeybee combs，Proc.Natl.Acad.Sci.21（2010）9502-9506.

［16］G.Karam，L.Gibson，Elastic buckling of cylindrical shells with elastic cores—I.Analysis，Int.J.Solids Struct.8（1995）1259-1283.

［17］G.Karam，L.Gibson，Elastic buckling of cylindrical shells with elastic cores—II.Experiments，Int.J.Solids Struct.8（1995）1285-1306.

［18］H.Obrecht，P.Fuchs，U.Reinicke，B.Rosenthal，M.Walkowiak，Influenceofwall constructions on the load-carrying capability of light-weight structures，Int.J.Solids Struct.6（2008）1513-1535.

［19］H.Obrecht，B.Rosenthal，P.Fuchs，S.Lange，C.Marusczyk，Buckling，postbuckling and imperfection-sensitivity:Old questions and some new answers，Comput.Mech.6（2006）498-506.

［20］H.Fan，F.Jin，D.Fang，Mechanical properties of hierarchical cellular materials.Part I:Analysis，Compos.Sci.Technol.15（2008）3380-3387.

［21］Hibbitt，Karlsson，Sorensen，ABAQUS/Standard User’s Manual，Hibbitt，Karlsson&Sorensen，2001.

［22］C.Chen，T.Lu，N.Fleck，Effect of inclusions and holes on the stiffness and strength of honeycombs，Int.J.Mech.Sci.2（2001）487-504.

［23］Guide M U s.，The Mathworks.，Inc.，Natick，MA，1998.

［24］Bo Wang，Youwei Chen，Yunfeng Shi，Imperfection sensitivity of in-plane modulus for hierarchical honeycombs，AMCS 31（2014）495-504.

3 July 2014

∗.

E-mail address:ET8001@126.com（Y.Shi）.

http://dx.doi.org/10.1016/j.taml.2015.05.004

2095-0349/©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http://creativecommons.org/licenses/by-nc-nd/4.0/）.

*This article belongs to Solid Mechanics.