Structural optimum design of bistable cylindrical shell for broadband energy harvesting application

Yong Wang，Liming Peng，Zhilong Huang

Department of Engineering Mechanics，Zhejiang University，Hangzhou 310027，China

Structural optimum design of bistable cylindrical shell for broadband energy harvesting application

Yong Wang，Liming Peng，Zhilong Huang∗

Department of Engineering Mechanics，Zhejiang University，Hangzhou 310027，China

A R T I C L E I N F O

Article history:

Accepted 12 May 2015

Available online 29 May 2015

Structural optimum design

Bistable cylindrical shell

Broadband energy harvesting

Harvestable power

Universal design curve

The shallow cylindrical structure is suitable to develop broadband vibration energy harvesters due to the property of the inherent mechanical bistability.In this letter，the optimum design of the bistable cylindrical shell for broadband energy harvesting application is investigated from the structural point of view.The output power is evaluated by the concept of the harvestable power，which balances the frequency of snap through and the referred output energy associated with each snap through.The nondimensionalharvestablepowerisanalyticallyexpressedasthefunctionofthenon-dimensionalcurvature parameterandoneconstructedparameter.Theuniversaldependenceoftheoptimalcurvatureparameter and the associated optimal harvestable power on the constructed parameter is derived，which can be well approximated by the linear relation in double logarithmic coordinate.

©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http://creativecommons.org/licenses/by-nc-nd/4.0/）.

According to the aufbau principle of bistable potential shape，the bistable harvesters can be classified as three categories，i.e.，the magnetic attraction，magnetic repulsion and mechanical bistability［8］.The bistable harvesters with magnetic components require the obtrusive arrangement of magnets and inevitably generate unwanted electromagnetic field，which dramatically limits the miniaturizationanddegradestheperformance.Thetypicalbistable harvesters with mechanical bistability are achieved through buckled mechanism，such as the clamped or hinged beam buckled by an axial force beyond the critical buckling force［10-12］and the inverted clamped beam buckled by the gravity of an elaborately selected tip mass［13］.Recently，a novel bistable harvester utilizing composite laminates with an asymmetric lay-up has been suggested［14-16］.The inherent mechanical bistability means asymmetric composite laminates occupy smaller space and induces that this type bistable harvester is potentially more suitable for miniaturization than the bistable harvesters with magnet-induced bistability.Furthermore，the structures with inherent mechanical bistability can be easily fabricated through strain mismatch，which is a mature technique in the micro electronics industry［17］.

The broadband response of the bistable harvester comes down to the solution of a set of essentially electromechanical coupling equations.The broadband response and parameter optimization have been investigated through some established techniques，such as Monte Carlo simulation，moment method，Galerkin procedure，finite element method and equivalent linearization technique［6，8，18-21］.All above mentioned are numerical or semi-analytical techniques，and so far not any analytical technique has been established unless confining the large ratio between the period of the mechanical subsystem and the time constant of the harvesting circuit［7］.Besides，most works contribute to the optimum designof the mathematical system，not the practical physical system.As an exclusive work toward the optimum design of the bistable harvester with inherent mechanical bistability，the authors discover the optimal configuration based on the statics of the device，not the practical broadband response［16］.

The isotropic cylindrical structure，as a common structure with inherent mechanical bistability，is more easily fabricated through microelectronic process than the asymmetric composite laminates.Similar to the bistable harvester with asymmetric compositelaminates，theisotropiccylindricalshellintegratedwithagroup of piezoelectric patches constitutes a simple and reliable bistable harvester，as shown in Fig.1.The host structure vibrates under the stimulation of the external excitation，and the piezoelectric patches deform and generate electric output through piezoelectric mechanism.This letter concentrates on the optimum design of the cylindrical shell-type bistable harvester，and tries to analytically establish the universal design curves.Due to the randomness of broadband excitation and the complexity of the electromechanical coupling，it is almost impossible to analytically optimize the actual output power.Based on the above consideration，we neglect the influence of the piezoelectric components and the harvesting circuitonstructuralresponsesandestablishtheoptimumdesignonly from the structural point of view.

Fig.1.Shallow cylindrical structure integrated with piezoelectric patches.

Consider a shallow cylindrical shell of thickness h，curvature radius R，and span b with two opposite edges hinged support.The uniformly distributed pressureξ（t）acting radially inwards is broadband excitation and approximately described by Gaussian white noise with the intensity 2D.With the assumption that the shell is sufficiently flat，the transverse deflection is represented by the fundamental mode，i.e.，w（y，t）=hq（t）sin（πy/b），in which q（t）denotes the non-dimensional amplitude of the transverse deflection［22］.The in-plane displacementv（y，t）can be expressed through the amplitude q（t）by integrating the inplane equilibrium equation and applying the boundary conditions v（0，t）=v（b，t）=0，i.e.，v=hq［-πhqsin（2πy/b）/（8b）+ b（1-cos（πy/b））/（πR）-2y/（πR）］，and then the strain energy per unit length is calcul ated by，in which，E andυ denote the plane-strain modulus，Young’s modulus and Poisson’s ratio，respectively.k=b2/（Rh）isanon-dimensionalcurvatureparameter which can measure the value of curvature radius.The kinetic energy per unit length is T=bmh2/4 and the dissipation function is Df=bh2/2，in which，m denotes the mass per unit mid-surface area andεrepresents the coefficient of viscous damping.The generalized force associated with the time-dependent randomexcitationisexpressedas，Q=2bhξ（t）/π.Then，thenonlinear stochastic differential equation which describes the random responses of the shallow cylindrical structure is derived through the Lagrange procedure［23，24］

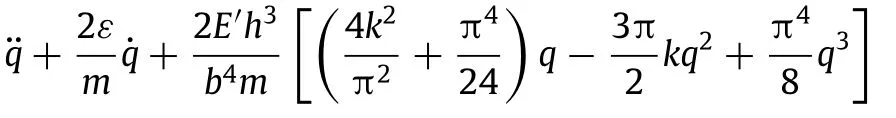
The equilibrium configuration of the shallow cylindrical structure free from external excitation should be first investigated.Removingtheacceleration，velocityandtheexternalexcitationterms from Eq.（1）yields the following algebraic equation，

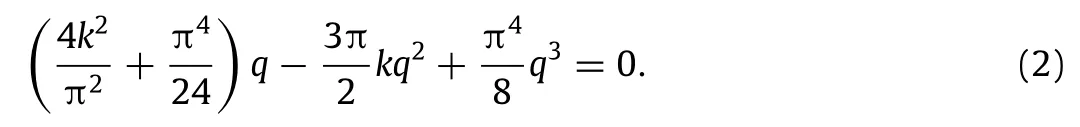
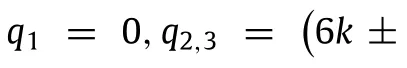
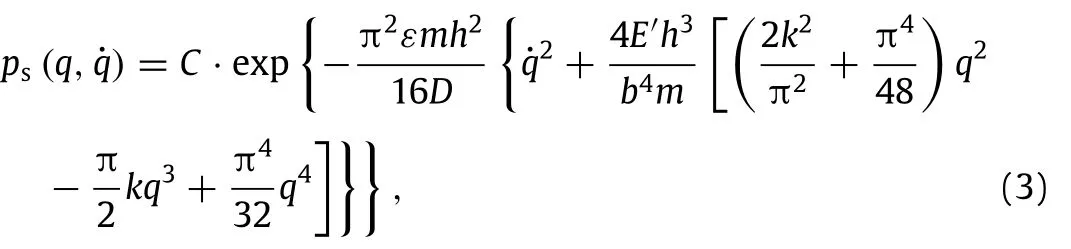
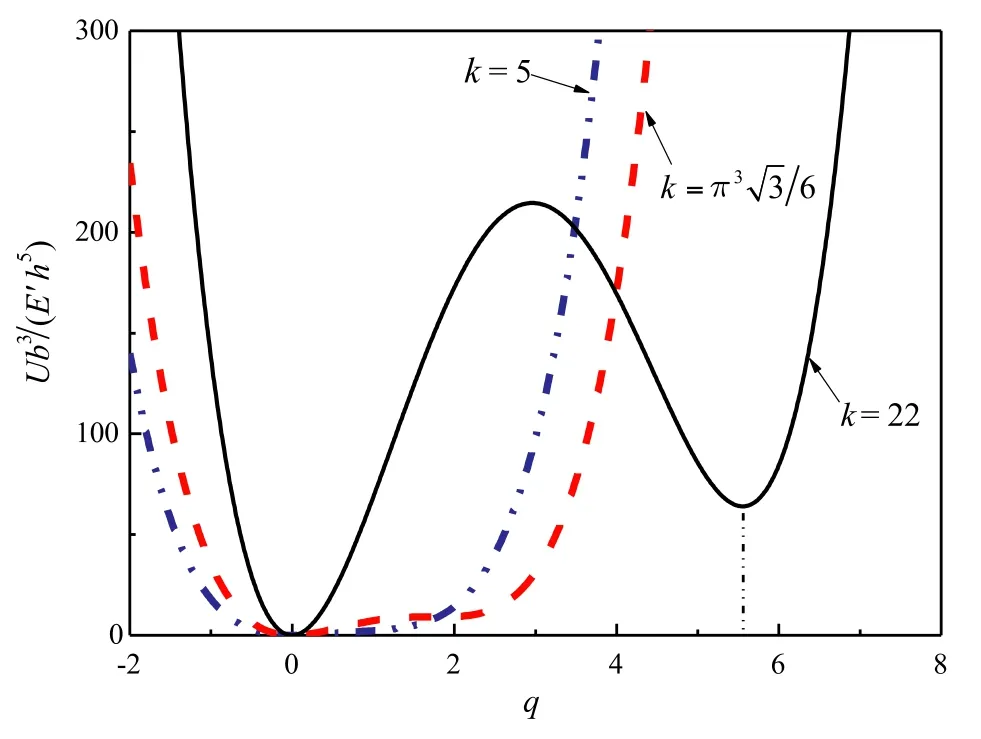
Fig.2.Asymmetrical potential shapes for representative values of curvature parameter k.

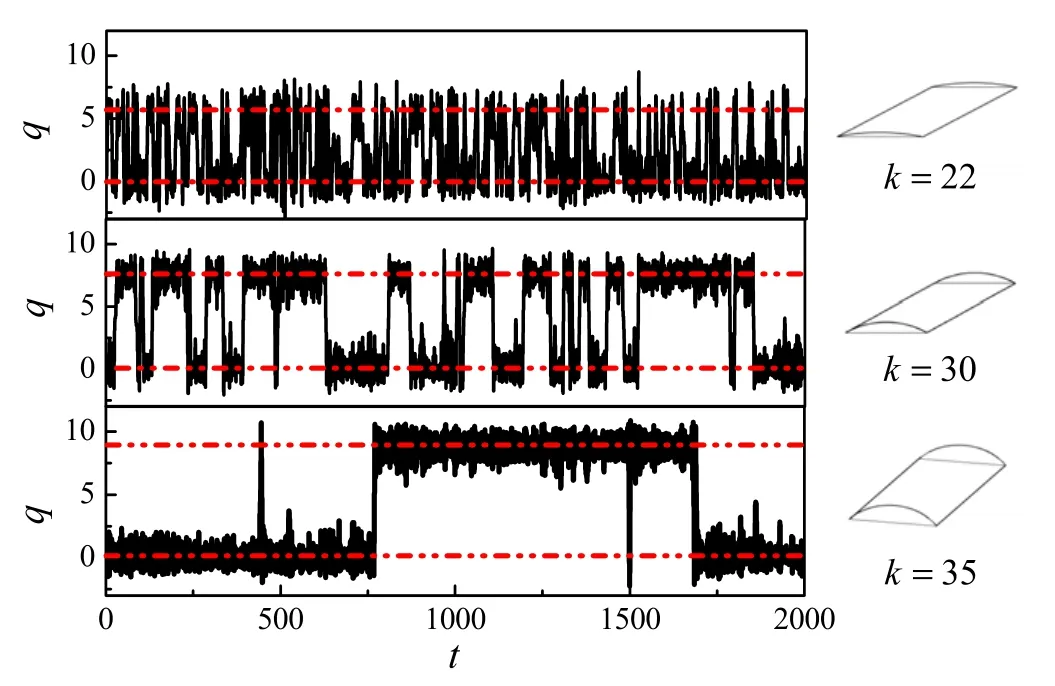
Fig.3.Response samples of the shallow cylindrical structure excited by the Gaussian white noise.System parameters are set asε/m=0.15，D=0.05，，and k=22，30，35.Dashed lines represent the stable equilibrium positions.

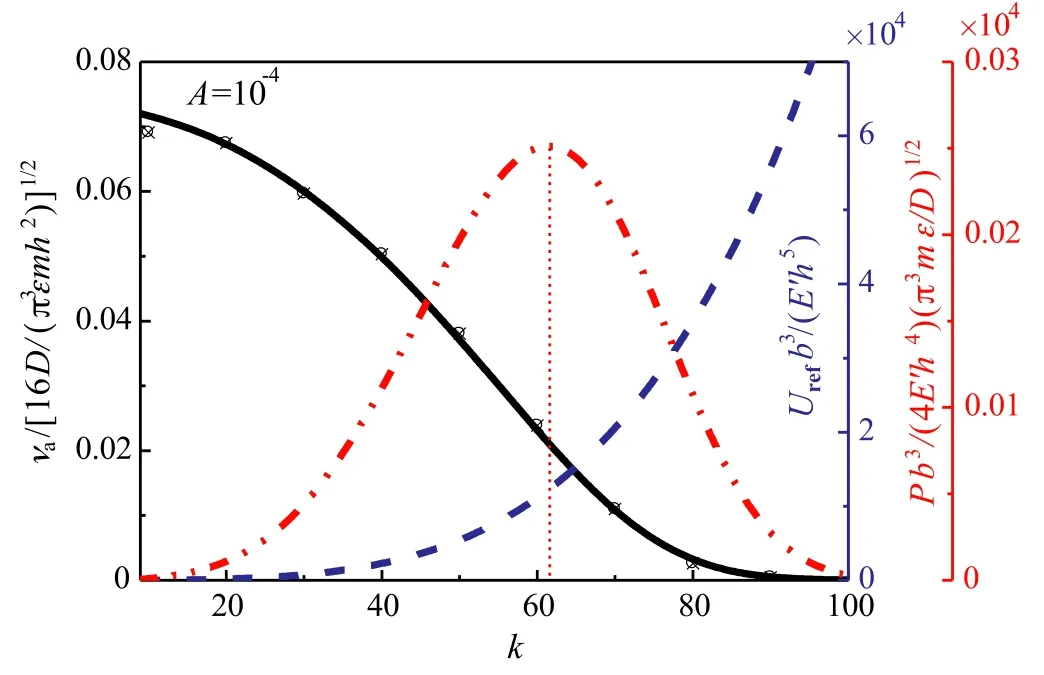
Fig.4.Dependence of the stationary ratio of expectation crossingνa，referred deformation energy Urefand harvestable power P on the curvature parameter k.Disperse markers denote the results from Monte Carlo simulation.

The output energy associated with each snap through can be evaluated by a referred deformation energy.The referred deformation energy is defined by the strain energy as the shallow cylindrical shell located in the plane specified by two straight edges，i.e.，

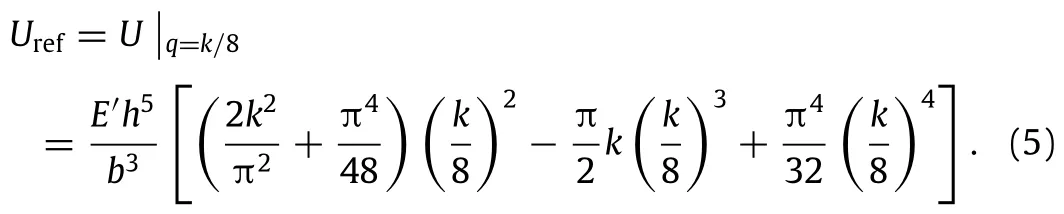
The referred deformation energy increases with the curvature parameter k，as shown in Fig.4.To balance the stationary ratio of expectation crossing and the referred deformation energy，the concept of the harvestable power is introduced as

The curvature parameter k is then optimized by maximizing the harvestable power.By substituting Eqs.（4）and（5）into Eq.（6），the harvestable power is explicitly expressed as

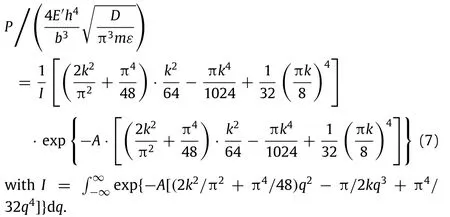
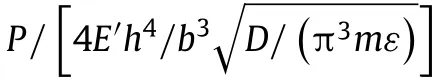
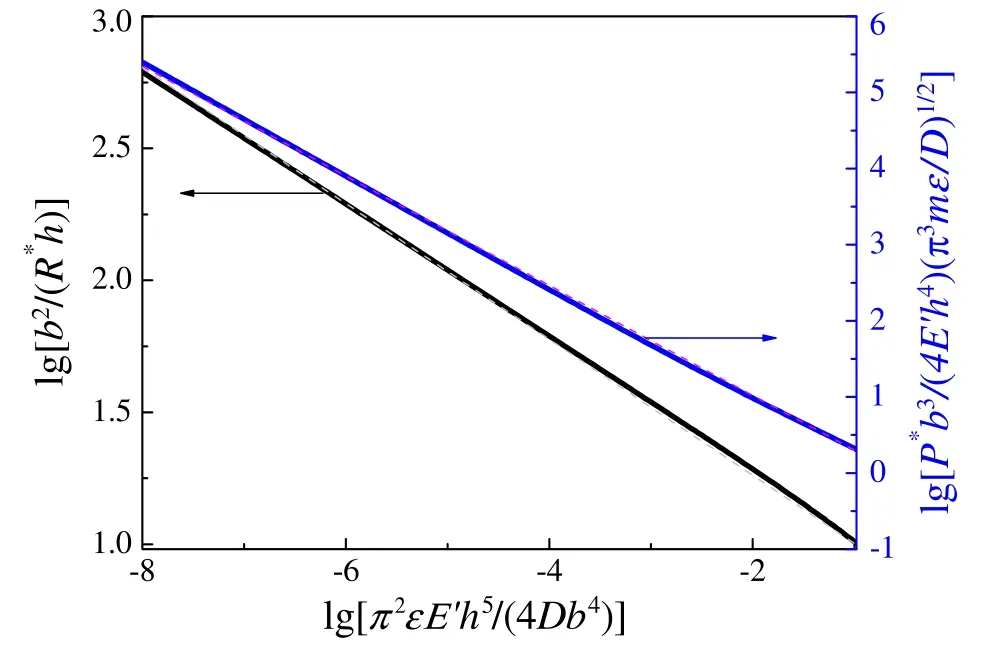
Fig.5.Dependence of the optimal curvature parameter b2/（R∗h）and the associated optimal harvestable poweron the constructed parameterεπ2E′h5/.Dashed lines denote the results of linear fitting.

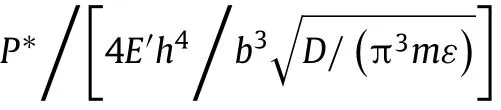
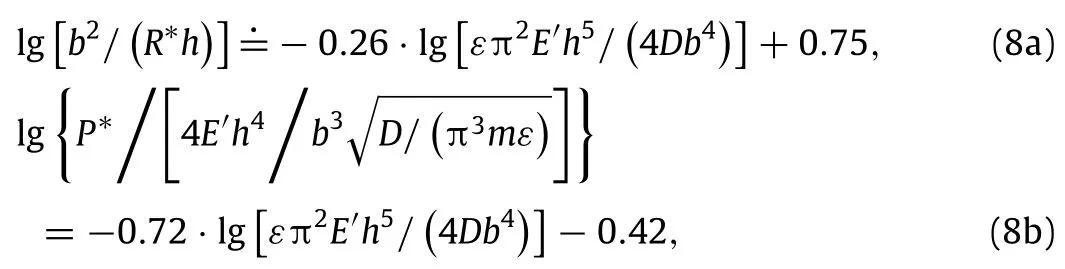
in which the values of slope and intercept are universal constants although they are derived by linear fitting.Once the geometric parameters h and b，material properties E′andε，and noise intensity 2D are assigned，the optimal curvature radius R∗can be directly derived through Eq.（8a）.The optimal harvestable power P∗associated with the optimal curvature radius R∗，which is determined by Eq.（8b），can be used to evaluate the upper bound of the mean output power by piezoelectric patches attached.

In summary，this letter investigated the optimum design of the cylindrical shell-type bistable harvester with the goal of maximizing the performance.By introducing the concept of harvestable power to balance the frequency of snap through and the referred output energy associated with each snap through，the universal dependence of the optimal curvature parameter and the associated optimal harvestable power on one constructed parameter is analytically established.The universal relations can be directly used to design the curvature radius of the cylindrical shell under arbitrarily given geometric，material and excitation parameters.It is worth pointing out that the optimum design was established based on the structural point of view and neglecting the influence of piezoelectric patches and the harvesting circuit.Asaresult，theoptimaldesignparameterprovidedbytheuniversal relations is only a sub-optimal result.

Acknowledgments

This work was supported by the National Natural Science Foundation of China（11472240，11302064，and 11321202）and the Fundamental Research Funds for the Central Universities（2014QNA4034）.

References

［1］S.Roundy，P.K.Wright，A piezoelectric vibration based generator for wireless electronics，Smart Mater.Struct.13（2004）1131-1142.

［2］S.P.Beeby，M.J.Tudor，N.M.White，Energy harvesting vibration sources for microsystems applications，Meas.Sci.Technol.17（2006）R175-R195.

［3］Y.Wang，T.Ma，H.Y.Yu，et al.，Random analysis on controlled buckling structure for energy harvesting，Appl.Phys.Lett.102（2013）041915.

［4］L.Tang，Y.Yang，C.K.Soh，Toward broadband vibration-based energy harvesting，J.Intell.Mater.Syst.Struct.21（2010）1867-1897.

［5］D.Zhu，M.J.Tudor，S.P.Beeby，Strategiesforincreasingtheoperatingfrequency range of vibration energy harvesters:a review，Meas.Sci.Technol.21（2010）022001.

［6］F.Cottone，H.Vocca，L.Gammaitoni，Nonlinear energy harvesting，Phys.Rev.Lett.102（2009）080601.

［7］M.F.Daqaq，R.Masana，A.Erturk，etal.，Ontheroleofnonlinearitiesinvibratory energyharvesting:acriticalreviewand discussion，Appl.Mech.Rev.66（2014）040801.

［8］S.P.Pellegrini，N.Tolou，M.Schenk，et al.，Bistable vibration energy harvesters: a review，J.Intell.Mater.Syst.Struct.24（2013）1303-1312；R.L.Harne，K.W.Wang，A review of the recent research on vibration energy harvesting via bistable systems，Smart Mater.Struct.22（2013）023001.

［9］B.P.Mann，D.AW.Barton，B.AM.Owens，Uncertainty in performance for linear and nonlinear energy harvesting strategies，J.Intell.Mater.Syst.Struct.23（2012）1451-1460.

［10］R.Masana，M.F.Daqaq，Electromechanical modeling and nonlinear analysis of axially loaded energy harvesters，ASME J.Vib.Acoust.33（2011）011007.

［11］R.Masana，M.F.Daqaq，Energy harvesting in the superharmonic frequency region of a twin-well oscillator，J.Appl.Phys.111（2012）044501.

［12］R.Masana，M.F.Daqaq，Response of duffing-type harvesters to band-limited noise，J.Sound Vib.332（2013）6755-6767.

［13］M.I.Friswell，S.F.Ali，O.Bilgen，et al.，Non-linear piezoelectric vibration energy harvesting from a vertical cantilever beam with tip mass，J.Intell.Mater.Syst.Struct.23（2012）1505-1521.

［14］A.F.Arrieta，P.Hagedorn，A.Erturk，et al.，A piezoelectric bistable plate for nonlinear broadband energy harvesting，Appl.Phys.Lett.97（2010）104102.

［15］A.F.Arrieta，T.Dlepero，A.E.Bergamini，et al.，Broadband vibration energy harvesting based on cantilevered piezoelectric bi-stable composites，Appl.Phys.Lett.102（2013）173904.

［16］D.N.Betts，H.A.Kim，C.R.Bowen，etal.，Optimalconfigurationofbistablepiezocomposites for energy harvesting，Appl.Phys.Lett.100（2012）114104.

［17］L.B.Freund，S.Suresh，Thin Film Materials:Stress，Defect Formation，and Surface Evolution，Cambridge University Press，Cambridge，2003.

［18］M.F.Daqaq，On intentional introduction of stiffness nonlinearities for energy harvesting under white Gaussian excitations，Nonlinear Dynam.69（2012）1063-1079.

［19］W.Martens，U.von Wagner，G.Litak，Stationary response of nonlinear magneto-piezoelectric energy harvester systems under stochastic excitation，Eur.Phys.J.Spec.Top.222（2013）1665-1673.

［20］P.Kumar，S.Narayanan，S.Adhikari，et al.，Fokker-Plank equation analysis of randomly excited nonlinear energy harvester，J.Sound Vib.333（2014）2040-2053.

［21］Q.He，Nonlinear Energy Harvesting Under White Noise，（Master thesis），Clemson University，Clemson，2013.

［22］H.N.Pi，S.T.Ariaratnam，W.C.Lennox，First-passage time for the snap-through of a shell-type structure，J.Sound Vib.14（1971）375-384.

［23］V.V.Bolotin，RandomVibrationofElasticSystems，MartinusNijhoffPublishers，Hague，1984.

［24］L.D.Landau，E.M.Lifshitz，Mechanics，Pergamon Press，Oxford，1969.

［25］E.Halvorsen，Fundamental issues in nonlinear wideband-vibration energy harvesting，Phys.Rev.E 87（2013）042129.

［26］Y.K.Lin，Probabilistic Theory of Structural Dynamics，McGraw-Hill Book Company，New York，1967.

［27］Y.K.Lin，G.Q.Cai，Probabilistic Structural Dynamics:Advanced Theory and Application，McGraw Hill，New York，1995.

6 September 2014

∗.

E-mail address:zlhuang@zju.edu.cn（Z.Huang）.

http://dx.doi.org/10.1016/j.taml.2015.05.003

2095-0349/©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http://creativecommons.org/licenses/by-nc-nd/4.0/）.

Vibration energy harvesting technique has extensive attention due to its important significance in different fields of technologysuchaswirelesssensors，datatransmittersandmedical implants［1-3］.Conventional linear harvesters utilize the principle of linear resonance and thus operate well only when the external excitation frequency matches to the fundamental frequency of the device.The time-varying，multi-frequency and random characteristics of the ambient vibration，however，render the typical linear harvesters unsuitable for most practical applications［4，5］.To address this issue，energy harvesting technique exploiting stiffness nonlinearity has been proposed for broadband transduction［6，7］.Compared to the nonlinear monostable harvesters，the bistable harvesters exhibit broader effective frequency bandwidth andlargeroutputpowerrelyingonthefantasticdynamicphenomena［7，8］.It is even more important that the bistable harvesters exhibit the highest robustness to the changing excitation environment and the uncertainty of design parameters compared to the linear and nonlinear monostable harvesters［8，9］.The advantages mentioned above verify the applicability of the bistable harvesters on the broadband energy harvesting.

*This article belongs to the Dynamics and Control