一种改进掩膜信号法及其在车桥振动响应信号中的应用

凌立鹏，毛 毳，李长跃

（1.天津城建大学 土木工程学院，天津 300384； 2.天津大学 建筑工程学院，天津 300384）

一种改进掩膜信号法及其在车桥振动响应信号中的应用

凌立鹏1，毛 毳1，李长跃2

（1.天津城建大学 土木工程学院，天津 300384； 2.天津大学 建筑工程学院，天津 300384）

针对经验模态分解法中存在的模态混叠问题，在掩膜信号法研究的基础上，通过编制掩膜信号幅值与频率确定程序，提出了一种改进掩膜信号法，并通过两个仿真实例进行了验证。其在车桥振动响应信号中的应用结果表明：在没有噪声处理的情况下，该方法可以大致得到信号中非平稳的基频响应信号组份，并且该组份具有定位间断事件的能力，这为车桥振动响应信号的处理提供了一个新的研究途径。

振动与波；经验模态分解；模态混叠；掩膜信号；车桥振动

在传统的信号处理中，信号需满足平稳、线性的假设。而实际信号大多是频率随时间、幅值的变化而变化的信号，即非平稳、非线性信号。目前对该类信号的处理和时频分析成为一种发展趋势[1,2]。对此，美籍华人Huang提出一种根据特征时间尺度对该类信号进行自适应分解的方法，并得到了具有物理意义的瞬时频率，形成了一种对该类信号进行有效处理和时频分析的方法[3]。这种自适应分解的信号处理方法称为经验模态分解法，简称EMD法。该方法诞生的同时，也伴随产生了一些问题，如模态混叠问题、端点效应问题和包络线拟合问题等[4]。

其中，模态混叠问题是指通过EMD法得到的固有模态函数（Intrinsic Mode Function,IMF）由于包含有不同模态组份而引起的信号分解问题。它最早是Huang在对含有间断频率组份的信号应用EMD法分解时发现的，从而确定间断信号是引起模态混叠问题发生的原因之一[3]。随后，Rilling[5]、Wu[6]、Yang[7]和胡爱军[8]等人相继对模态混叠问题进行了研究，发现噪声、密集模态组份和端点效应问题引起的包络曲线“过冲”也是模态混叠问题发生的重要原因。

借此，诸多专家和学者相继提出了解决模态混叠问题的方法[9-13]。其中，掩膜信号法以其具有的计算效率高、间断信号分解能力强和后处理相对简单等特点而备受关注。为此，在掩膜信号法研究的基础上，通过编制掩膜信号幅值与频率确定程序，提出并实现了一种改进掩膜信号法，并在车桥振动响应信号中得到了应用。

1 改进掩膜信号法

1.1 掩膜信号法的原理与分析

Deering等人[12]对在不同频率比和不同幅值比组合下两信号的经验模态分解结果研究的基础上，提出了一种掩膜信号法。其基本原理就是通过在原信号中加入合适掩膜信号来近似改变原信号的极值点分布，进而改善经验模态分解结果，消除模态混叠现象，达到解决模态混叠问题的目的。但在合适掩膜信号的频率与幅值选择上存在困难，对此，国外的Senroy[14]、Laila[15]和国内的赵玲[16]、杨贤昭[17]等人对该方法相继进行了一些研究与改进。本文从掩膜信号的频率与幅值选择过程是典型的双参数确定问题角度出发，通过定义相关变量与参考信号，利用自主编制的掩膜信号幅值与频率确定程序，实现了一种掩膜信号幅值与频率的确定方法，进而实现了一种改进掩膜信号法。

1.2 掩膜信号幅值与频率确定程序

EMD法的目的在于得到一个不包含模态混叠问题影响的单一模态组份信号，在已知信号中存在某单一模态组份的前提下，就可以通过将该模态组份作为参考信号，将加入掩膜信号后的原信号经过EMD法得到的分解结果逐一与其进行匹配，匹配程度越高，说明加入掩膜信号后的原信号经过EMD法得到的分解结果受模态混叠问题的影响越小，即加入的掩膜信号幅值与频率为最合适的选择组合，从而得到了合适掩膜信号，这就是掩膜信号幅值与频率确定程序的原理。

其中，两信号匹配程度XOR(X1,X2)是应用统计学中的相关系数算法与图像匹配算法相结合而提出的，具体是通过下式计算得到的。

式中X1(n)代表分解结果，为加入掩膜信号后的原信号经过EMD法分解得到的；X2(n)代表参考信号，为原信号中不包含模态混叠问题影响的模态组份信号，通过上式不难发现，两信号匹配程度计算值越近1，说明两信号的频率与波形相似程度越高。

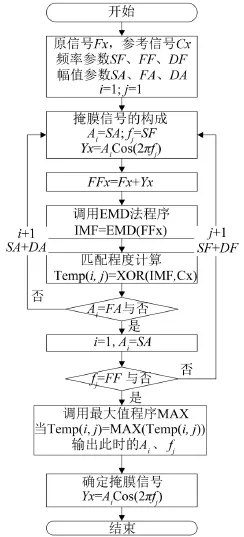
图1 掩膜信号幅值与频率确定程序

但原信号中不包含模态混叠问题影响的单一模态组份信号是很难获知的。对此，根据带通滤波法具有的简单、高效的频带控制能力，对原信号经过经验模态分解得到分解结果进行幅频谱分析，并应用带通滤波得到信号中大致不受模态混叠问题影响的单一模态组份信号，并将此模态组份信号作为两信号匹配程度的计算依据，以此作为掩膜信号幅值与频率的确定过程，并通过MATLAB语言编制了该过程的实现程序，程序流程具体如下图2所示。

图中，频率参数SF代表掩膜信号起始试算频率值；FF代表掩膜信号终止试算频率值；DF代表试算频率值精度；幅值参数AF代表掩膜信号起始试算幅值；AF代表掩膜信号终止试算幅值，AF代表试算幅值精度；Yx代表构成的掩膜信号；Ai代表掩膜信号第i个试算幅值；fi代表掩膜信号第i个试算频率值；Temp(i,j)代表掩膜信号第i个试算幅值与第j个试算频率值组合时，分解结果IMF与参考信号Cx的匹配程度计算值；EMD法的计算程序[2]和最大值的计算程序MAX考虑到目前比较通用，就不再详述。

1.3 改进掩膜信号法的实现过程

考虑端点效应问题引起包络曲线的“过冲”也会引起模态混叠问题的发生，提出一种中心对称延拓改进措施，具体就是在原信号两端的零值点处放置“镜面”，然后进行以端点为中心的中心对称延拓。结合上节通过带（低）通滤波法得到的参考信号和掩膜信号幅值与频率确定程序，从而实现了改进掩膜信号法，具体过程如下：

（1）对原信号应用中心对称延拓改进措施；

（2）对延拓后信号经过经验模态分解得到的分解结果进行幅频谱分析，大致确定其中不受模态混叠问题影响的单一模态组份信号的频带范围，从而通过带通滤波法将其作为参考信号；

（3）通过应用掩膜信号幅值与频率确定程序，得到合适掩膜信号的频率与幅值组合，确定掩膜信号；

（4）将确定的掩膜信号加入延拓后信号再次应用EMD法，得到分解结果；

（5）去除分解结果中所加的掩膜信号，得到最终的分解结果。

2 仿真实验验证

2.1 仿真实验一

为说明改进掩膜信号法及其信号处理效果，假设采样频率为400 Hz，采样时长为0～0.5 s，仿真信号为y(t)=sin(200πt)+sin(120πt)[15]，应用中心对称延拓改进措施，得到延拓后信号，具体如下图3所示。

图2 信号y(t)及延拓后信号示意图

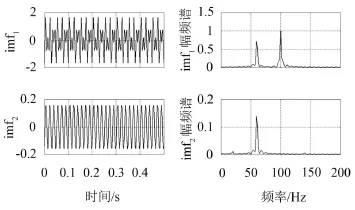
图3 EMD法分解结果及对应的幅频谱

对延拓后信号通过EMD法得到分解结果imf1和imf2及其对应的幅频谱，如图3中所示。

通过分解结果的观察，不难发现：分解结果imf2为大致不受模态混叠问题影响的单一模态组份信号，不难确定其频带段，通过带通滤波法从原信号获得该频带段信号为参考信号，如图4所示。

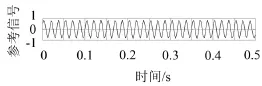
图4 参考信号

应用掩膜信号幅值与频率确定程序，通过试算发现，掩膜信号幅值固定时，掩膜信号频率值在0～Fs/2和Fs/2～Fs是等价的，因此，一般终止试算频率值FF采用Fs/2即可。最终在计算精度为0.1时，得到掩膜信号频率值约取140.0 Hz，幅值约取3.1倍原信号最大幅值时，分解结果与参考信号的匹配程度可达到最大值0.99，从而将140.0 Hz和3.1倍原信号最大幅值确定为掩膜信号频率值与幅值组合。

将确定的掩膜信号加入延拓后的信号，再次应用EMD法得到分解结果，并去除分解结果中包含的掩膜信号，得到最终的分解结果，下图5所示。

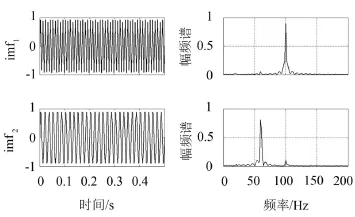
图5 改进掩膜信号法的分解结果及对应的幅频谱

从图中不难看出，分解结果与文献[15]得到的分解结果基本相同，并且达到了解决模态混叠问题的目的。

(谢安)与王羲之及高阳许询，桑门支遁游处，出则渔弋山水，入则言咏属文，无处世意。……又于土山营墅，楼馆林竹甚盛，每携外子侄往来游集。[9](《谢安传》，P2072)

2.2 仿真实验二

为验证该方法对含有间断频率组份信号的分解能力，对某含有间断拍波的信号z(t（)图6）应用该方法进行了分析。

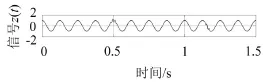
图6 含有间断拍波的信号z(t)

为方便说明改进掩膜信号法对分解结果的提高，应用不加改进的EMD法对该信号进行了分解，考虑到该信号属于非平稳信号，同时做出了分解结果对应的Hilbert时频谱图，如图7所示。

图7 EMD法的分解结果及对应的Hilbert时频谱

从图8中，不难发现，分解结果存在严重的模态混叠问题。为此，应用提出的改进掩膜信号法，计算发现：当掩膜信号频率值取50.0 HZ，幅值取1.6倍信号最大幅值时，分解结果与参考信号的匹配最好。从而做出了得到的最终分解结果，如图8所示。

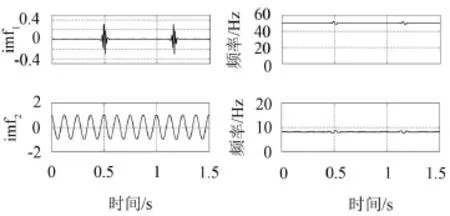
图8 改进掩膜信号法的分解结果及对应的Hilbert时频谱

通过图8与图9的观察，不难发现改进掩膜信号法对分解结果的改善效果是巨大的，不仅解决了分解结果中存在的模态混叠问题，而且提高了分解结果的时频分析能力，使时频分析结果更能反应出原信号中不同模态组份的时频变化情况。

3 在车桥振动响应信号中的应用

车桥振动响应信号是指当车辆荷载移动通过桥梁时，桥梁产生的动力响应信号。如果车辆质量相比于桥梁结构质量不可忽略，车辆质量位置的移动将导致车桥系统的质量矩阵发生变化，引起车桥系统的动力响应频率发生时变。此时，动力响应信号将是一种典型非平稳（时变）信号[18]。目前对该类信号进行时频分析的研究很少，为此，本文应用改进掩膜信号法做出了以下研究。

图9 车桥模型

已知该简支梁桥模型的基频在13.6 Hz附近，通过进行跑车试验，得到了该简支梁桥模型跨中位置的加速度响应信号及其对应的幅频谱图，如图10所示。

图10 车桥振动响应信号及其幅频谱图

不难发现图中基频附近的频带较宽，主要原因可能是由于基频的非平稳变化（时变）导致，但是具体变化情况不得而知。为此，应用改进掩膜信号法对该信号进行分析，通过对原信号进行合理延拓并应用EMD法，不难得到如图11所示的分解结果及其对应的幅频谱图。

通过观察，不难发现，imf2的主要频带信号组份频带位于信号基频附近且较宽，大致满足基频模态组份非稳定性的表现，为大致不受模态混叠问题影响的单一模态组份信号。因此，将带通滤波上限取14 Hz，下限取11 Hz对延拓后的原信信号进行滤波，最终得到参考信号，如图12所示。

通过掩膜信号幅值与频率确定程序，最终发现当合适掩膜信号频率为33.0 Hz，幅值为0.4倍信号最大幅值时，参考信号与分解结果的相关系数可以达到最大值0.920。从而确定了掩膜信号，并将其加入延拓后的原信号后再应用EMD法进行分解，从而得到最终的分解结果，见图13。

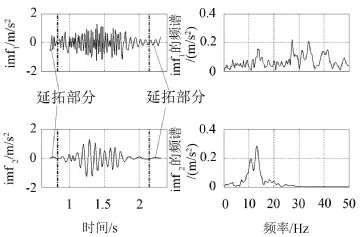
图11 原信号延拓后的EMD法分解结果

图12 参考信号

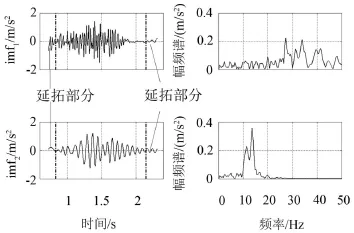
图13 改进掩膜信号法的分解结果

通过对比图11与图12，不难发现：

（1）改进掩膜信号法得到的imf1在基频频带附近对应的幅频谱值有所降低，imf2在基频频带附近对应的幅频谱值有所提高；

（2）改进掩膜信号法得到的imf2尾部出现明显的余振波形；

（3）改进掩膜信号法得到的imf2对应的幅频谱图的频带较窄。

说明改进掩膜信号法具有一定的模态混叠问题解决能力，分解结果得到的imf2更接近基频模态组份信号特点[18]且受噪声影响更小。

为更进一步分析实验结果，对imf2应用时频分析，得到如图14所示的Hilbert时频谱图。

图14 imf2对应的Hilbert时频图

通过观察，不难发现：①—⑤的瞬时频率大致经历了先逐渐下降后逐渐上升，最后趋于基频13.6 Hz附近的过程，这与移动车质量对车桥系统瞬时频率的影响大致相同[18]，进而解释了基频附近频带过宽原因是由于时变的基频变化导致的。

根据车过桥振动响应相关理论[19]和多组试验数据，进一步分析了图中突变点，发现：图中①与Hilbert变换中端点效应问题有关；图中②与试验车后轴上桥经过模型接缝的时刻相吻合；图中③与试验车前轴离桥时经过模型接缝的时刻相吻合；图中④与试验车后轴离桥时经过模型接缝的时刻相吻合；图中⑤与Hilbert变换中端点效应问题有关。

考虑到改进掩膜信号法本身具有的定位间断高频信号的能力，说明试验车前后轴经过模型接缝产生了间断高频信号。反过来，可以通过对该类信号时频突变时刻的分析，得到表征车辆与桥梁作用异常等间断事件发生的时刻和位置信息。

4 结语

针对EMD法中存在的模态混叠问题，提出并验证了一种改进的掩膜信号法，并应用该方法对车桥振动响应信号进行了分析，得出以下结论：

（1）提出的中心对称延拓措施在处理EMD法的端点效应问题上表现良好；

（2）改进掩膜信号法不仅可以解决EMD法的模态混叠问题，而且克服了传统掩膜信号法在掩膜信号频率和幅值选择方面的困难；

（3）该方法在处理含有噪声的车桥振动响应信号时，不需要对噪声进行预处理，便可大致分离出信号中非稳定的基频模态组份信号。

（4）分离出的基频模态组份信号的时频突变位置可以表征车过桥过程中间断异常事件发生的时间甚至位置信息，从而为车桥振动响应信号的处理提供了一种新的研究途径。

[1]Feldman M.Hilbert transform applications in mechanical vibration[M].The Atrimum,Southern Gate,Chichester, West Sussex,Po198SQ,United Kingdom:John Wiley& Sons,2011:1-285.

[2]范兴超，纪国宜.基于希尔伯特变换结构模态参数识别[J].噪声与振动控制，2014，34(3)：52-56.

[3]Huang N E,Shen Z,Long S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[C].Proceedings of the RoyalSociety ofLondon.Series A:Mathematical, Physical and Engineering Sciences,1998,454(1971):903-995.

[4]Huang N E,Shen Z,Long S R.A new view of nonlinear water waves:The Hilbert Spectrum 1[J].Annual Review of Fluid Mechanics,1999,31(1):417-457.

[5]Rilling G,Flandrin P,Goncalves P.On empirical mode decomposition and its algorithms[C].Proceedings of IEEE-EURASIP workshop on nonlinear signal and image processing NSIP-03(2003),France:INRIA.2003,3:8-11.

[6]Wu Z,Huang N E.A study of the characteristic of white noise using the empirical mode decomposition method[C]. Proceeding of the Royal Society of London.Series A: Mathematical,Physical and Engineering Sciences,2004, 460(2046):1597-1611.

[7]Yang Z,Yang L,Qing C,et al.A method to eliminate riding waves appearing in the empiricalAM/FM demodulation[J].Digital Signal Processing,2008,18(4): 488-504.

[8]胡爱军，孙敬敬，向玲.经验模态分解中的模态混叠问题[J].振动、测试与诊断，2011,31(4):429-434.

[9]Wu Z,Huang N E.Ensemble empiricalmode decomposition:a noise-assisted data analysis method[J]. Advances inAdaptive DataAnalysis,2009,1(01):1-41.

[10]Gao Y,Ge G,Sheng Z,et al.Analysis and solution to the mode mixing phenomenon in EMD[C].Image and Signal Processing(CISP08).Sanya,China:IEEE,2008,5:223-227.

[11]Li H,Yang L,Huang D.The study of the intermittency test filtering character of Hilbert-Huang transform[J]. Mathematics and Computers in Simulation,2005,70(1):22-32.

[12]Deering R,Kaiser J F.The use of a masking signal to improve empiricalmode decomposition[C].Acoustics, Speech,and SignalProcessing (ICASSP05).IEEE International Conference on:IEEE,2005,4:485-488.

[13]Tang B,Dong S,Song T.Method for eliminating mode mixing of empirical mode decomposition based on the revised blind source separation[J].Signal Processing, 2012,92(1):248-258.

[14]Senroy N,Suryanarayanan S.Two techniques to enhance empirical mode decomposition for power quality applications[C].Power Engineering Society General Meeting.Tampa,FL:IEEE.2007:1-6.

[15]Laila D S,Messina A R,Pal B C.A refined Hilbert-Huang transform with applications to interarea oscillation monitoring[J].PowerSystems,IEEE Transactions, 2009,24(2):610-620.

[16]赵玲，刘小峰，秦树人，等.消除经验模态分解中混叠现象的改进掩膜信号法[J].振动与冲击，2010，29(9):13-17.

[17]杨贤昭.基于经验模态分解的故障诊断方法研究[D].武汉：武汉科技大学信息科学与工程学院，2012.

[18]李伟钊.基于动力测试的公路混凝土梁式桥工作性能评定方法研究[D].哈尔滨：哈尔滨工业大学交通科学与工程学院，2012.

[19]吴延平，吴冬雁，谢旭，等.车辆通过钢箱梁桥伸缩缝的振动响应及减振[J].噪声与振动控制，2013，33(2)：95-100.

图10 软件仿真结果

参考文献：

[1]徐龙祥，朱均，虞烈.可倾瓦轴承支承的转子系统稳定性研究[J].应用力学学报，1987(4)：57-58.

[2]孙永明，吴士年，李海鹏.离心压缩机可倾瓦轴承油膜失稳解析[J].风机技术，2012(6)：73-75.

[3]刘兴星，孟再强，李明.可倾瓦轴承的油膜力模型及其特性分析[J].噪声与振动控制，2013，33（4）：59-63.

[4]孙加丰，荆建平，贾林.滑动轴承动态油膜压力的实时测量方法研究[J].噪声与振动控制，2013，33（4）：227-231.

[5]王丽萍.可倾瓦轴承动力学建模及动力特性研究[D].上海：复旦大学，2007.

[6]Issan A M,Maurice L A.Numerical study of some nonlinear dynamics of a rotor supported on a three-pad tilting pad journal bearing[J].Journal of Vibration and Acoustics,2005,127:262-272.

[7]王文，张直明.油叶型轴承非线性油膜力数据库[J].上海工业大学学报，1993（4）：299-305.

[8]张直明，谢友柏.滑动轴承的流体动力润滑理论[M].北京：高等教育出版社，1986：99-102.

[9]蔡林.流体动压滑动轴承静特性研究[D].哈尔滨：哈尔滨工程大学，2012.

An Improved Masking Signal Method and ItsApplication in Vehicle-bridge Vibration Response SignalAnalysis

LING Li-peng1,MAO Cui1,LI Chang-yue2
(1.Collage of Civil Engineering,Tianjin Chengjian University,Tianjin 300384,China; 2.School ofArchitectural Engineering,Tianjin University,Tianjin 300384,China)

For the mode mixing issue of the empirical mode decomposition(EMD)method,an improved masking signal method was proposed by programming the amplitude and frequency determination of the masking signal.This method was validated by two simulation experiments.Application of this method to the analysis of vehicle-bridge vibration response signal shows that the unsteady fundamental frequency response signal component can be obtained approximately without noise processing by using this method,and the component has the ability of positioning intermittent events.This method may provide a new research approach for signal processing of the vehicle-bridge vibration response.

vibration and wave;EMD;mode mixing;masking signal;vehicle-bridge vibration

TN911.7；U466

A

10.3969/j.issn.1006-1335.2015.03.033

1006-1355(2015)03-0153-06

2014－12－18

凌立鹏（1988－），男，河北廊坊人，硕士生，主要研究方向：桥梁振动响应信号处理与损伤识别。

毛毳，女，硕士生导师。E-mail:mctj2008@163.com