单一闭合中心裂隙对岩石单轴压缩破坏特征的影响

陈秀云

(黄淮学院 建筑工程学院，河南驻马店 463000)

1 研究背景

裂隙岩石的力学行为和破坏特征一直是岩石断裂力学中的研究热点之一。目前主要通过室内模型试验和数值模拟等方法研究裂隙岩石的强度特征和裂隙扩展规律。数值模拟方法相对于模型试验更易实现，在裂隙岩石破坏特征的研究中应用比较广泛。付金伟等［1］利用FLAC软件模拟和研究双裂隙岩石试件在单轴、双轴加载作用下的破坏过程;李瑶等［2］对含2条共面非贯通裂隙岩石的单轴压缩特性进行了数值模拟研究;杨圣奇等［3］采用颗粒流软件模拟了含单条中心直裂隙和断续双裂隙岩石的巴西试验;黄彦华等［4］采用颗粒流软件模拟了非共面双裂隙红砂岩宏细观力学行为;张社荣等［5］采用颗粒流软件模拟了含2条预制裂纹的岩石在双轴压缩试验下的裂纹扩展及破坏模式。但是，上述研究都将裂隙考虑为张开裂隙，而未考虑裂隙闭合对岩石破坏特征的影响。

本文采用颗粒流软件，考虑裂隙闭合，研究闭合裂隙的倾角、长度和摩擦系数对裂隙岩石破坏特征的影响。

2 数值模型

本文采用颗粒流模型模拟裂隙岩石的单轴压缩试验，以生成颗粒集合模拟岩石试样，闭合裂隙采用光滑节理模型表示，非闭合裂隙采用删除颗粒的方式表示。裂隙为摩擦裂隙，不考虑裂隙的黏结强度，只在光滑节理模型中添加摩擦力。数值试样高H=100 mm，宽W=50 mm，如图1(a)所示。通过对试样上下墙施加固定的方向相反、大小相同的速度，实现试样的单轴压缩加载。加载过程中，程序会自动记录模拟过程中试样所受荷载以及裂隙扩展过程。数值模拟中选择峰后强度为峰值强度70%时，数值试验停止。图1(b)为中心闭合裂隙的几何参数。

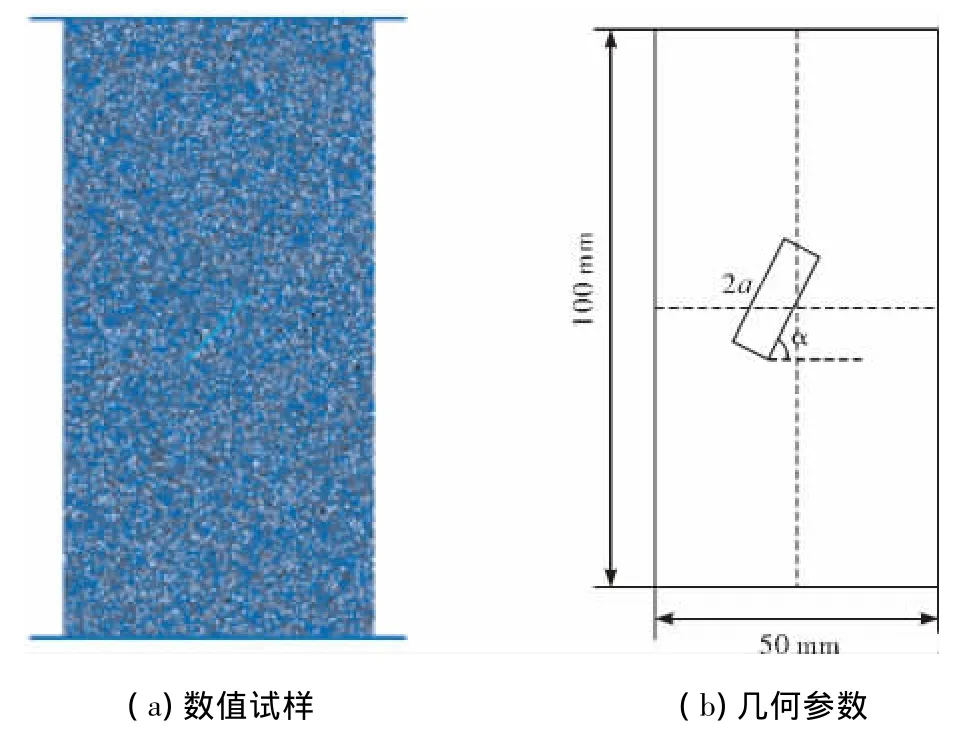
图1 含单一闭合中心裂隙岩石的数值试样和几何参数Fig.1 Numerical sample and geometric parameters of cracked rock containing single closed fissure

数值试样的细观参数选择如表1所示。

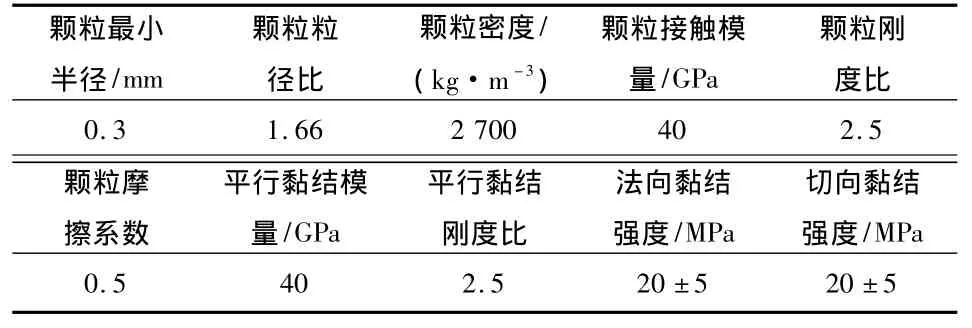
表1 PFC模拟采用的细观参数Table 1 Mesoscopic parameters of PFC simulation

本文模拟时采用以下4种方案:

(1)裂隙倾角α=45°，裂隙摩擦系数f=0，裂隙长度 2a=20 mm，裂隙宽度 b=4，3，2，1，0(闭合)。

(2)裂隙倾角 α=45°，裂隙摩擦系数 f=0.5，裂隙长度2a=5，10，15，20，25 mm，裂隙为闭合裂隙。

(3)裂隙倾角α=45°，裂隙长度2a=10 mm，裂隙摩擦系数 f=0，0.25，0.50，0.75，1，裂隙为闭合裂隙。

(4)裂隙倾角 α=0°，22.5°，45°，67.5°，90°，裂隙摩擦系数f=0.5，裂隙长度2a=10 mm，裂隙为闭合裂隙。

3 数值模拟结果分析

3.1 裂隙宽度对破坏特征的影响

首先实施方案(1)，研究裂隙宽度对裂隙岩石破坏特征的影响。图2是压缩条件下裂纹扩展方式，可以看出裂隙扩展一般产生3种类型的裂纹［6］:翼型裂纹(张拉裂纹)、共面次生裂纹(剪切裂纹)和次生斜裂纹(剪切裂纹)。本文中将这3种裂纹分别编号为①，②，③。

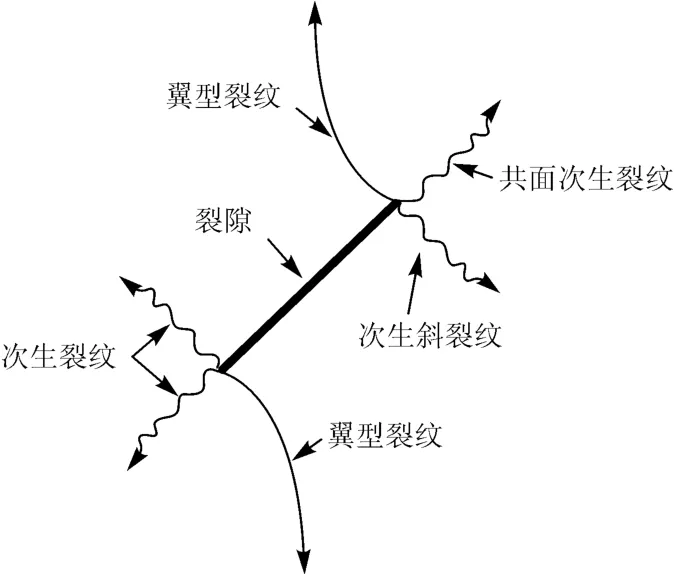
图2 压缩条件下裂纹扩展方式［6］Fig.2 Propagation of a crack subjected to compression［6］

图3给出了不同裂隙宽度下岩石的破坏模式。从图3中可以看出，完整岩石、含非闭合裂隙岩石和含闭合裂隙岩石的破坏模式存在明显区别:

(1)完整岩石中细观裂纹以拉裂纹为主，可认为是张拉破坏模式;裂隙岩石出现了3种类型的裂纹，其中翼型裂纹最先出现，都为细观拉裂纹，表现为张拉破坏扩展模式(Ⅰ型断裂扩展)。次生裂纹扩展之初出现了许多细观剪切裂纹，表现为剪切破坏模式(Ⅱ型断裂扩展)，但随着扩展的进行，出现了大量细观次生张拉裂纹，同时次生裂纹扩展到一定程度会发生偏转，转换为张拉破坏扩展(Ⅰ型断裂扩展)，并最终形成贯通破坏面(Ⅱ-Ⅰ型断裂扩展)。

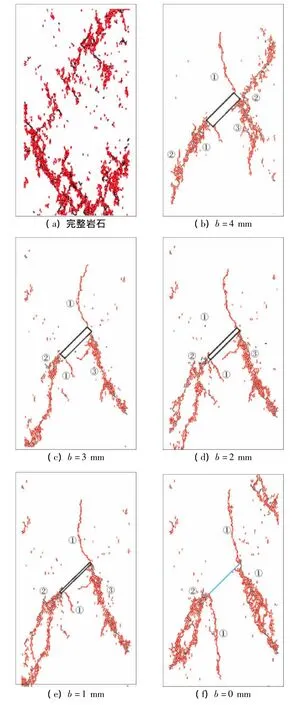
图3 不同裂隙宽度下岩石破坏模式(红色表示拉破坏、黑色表示剪破坏，下同)Fig.3 Failure modes of cracked rock with different fissure width(red indicates tensile failure，black indicates shear failure，similarly hereinafter)

(2)当裂隙宽度较大时b=4 mm，共面次生裂纹的扩展形成了裂隙岩石的贯通破坏面;当裂隙宽度b=3，2，1 mm时，裂隙的扩展模式基本相同，共面次生裂纹和次生斜裂纹的扩展形成了裂隙岩石的贯通破坏面。

(3)当裂隙宽度b=0，即裂隙闭合时，翼型裂纹的扩展长度和起裂角度明显不同于非闭合裂隙，但仍是共面次生裂纹和次生斜裂纹的扩展形成了裂隙岩石的贯通破坏面。

图4给出了不同裂隙宽度下岩石的峰值强度。

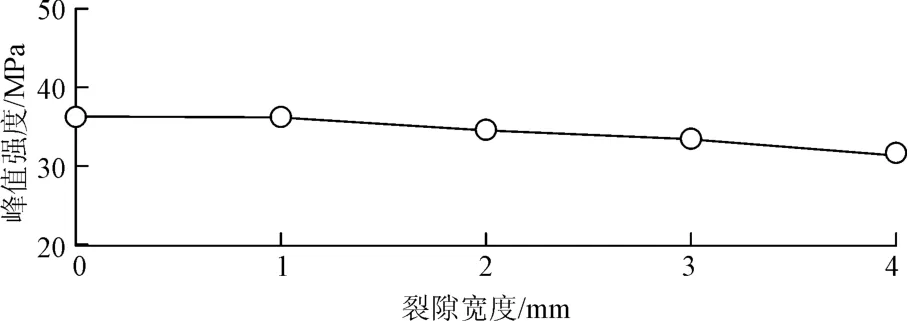
图4 不同裂隙宽度下岩石峰值强度Fig.4 Peak strength of cracked rock with different fissure widths

方案(1)中裂隙宽度b=0，1，2，3，4 mm 时，对应的峰值强度分别为36.34，36.02，34.42，33.22，31.29 MPa，而完整岩石的峰值强度为52.21 MPa。显然，随着裂隙宽度的增大，裂隙岩石的峰值强度逐渐减小。由此可知，裂隙闭合与否对裂隙岩石的强度和破坏特征都存在影响，当非闭合裂隙的宽度越小时，其强度和破坏模式越接近于闭合裂隙岩石。

3.2 裂隙长度对破坏特征的影响

实施方案(2)，研究裂隙长度对裂隙岩石破坏特征的影响。图5给出了不同裂隙长度下岩石的破坏模式。

从图5中可以看出，不同裂隙长度下，岩石的破坏模式存在明显区别:

(1)随着裂隙长度的减小，微裂纹产生的数量越多，裂隙岩石破坏模式越来越接近于完整岩石的破坏模式，特别是裂隙长度2a=5 mm，裂隙岩石与完整岩石破坏模式几乎相同，仅在裂隙尖端产生了少量翼型裂纹。

(2)2a=10，15 mm时，共面次生裂纹或次生斜裂纹的扩展形成了裂隙岩石的贯通破坏面(Ⅱ-Ⅰ型断裂扩展);2a=20 mm时，翼型裂纹的扩展形成了裂隙岩石的贯通破坏面(Ⅰ型断裂扩展);2a=25 mm时，共面次生裂纹的扩展形成了裂隙岩石的贯通破坏面(Ⅱ-Ⅰ型断裂扩展)。

图6给出了不同裂隙长度下岩石的峰值强度。

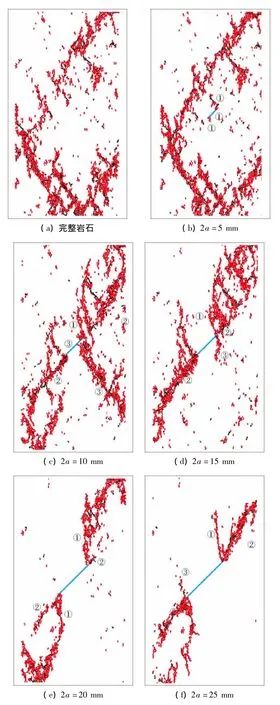
图5 不同裂隙长度下岩石破坏模式Fig.5 Failure modes of cracked rock with different fissure lengths

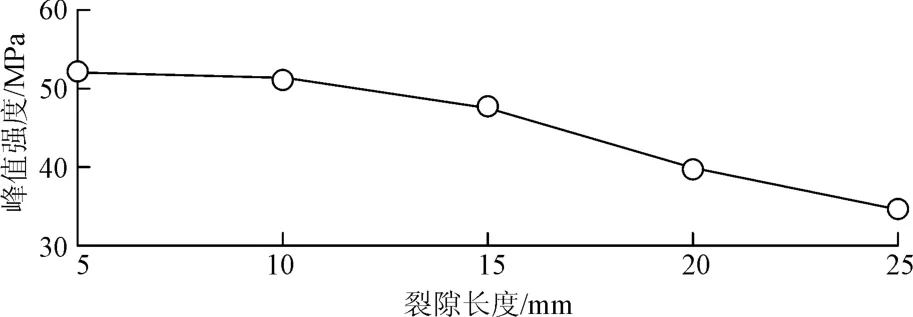
图6 不同裂隙长度下岩石峰值强度Fig.6 Peak strength of cracked rock with different fissure lengths

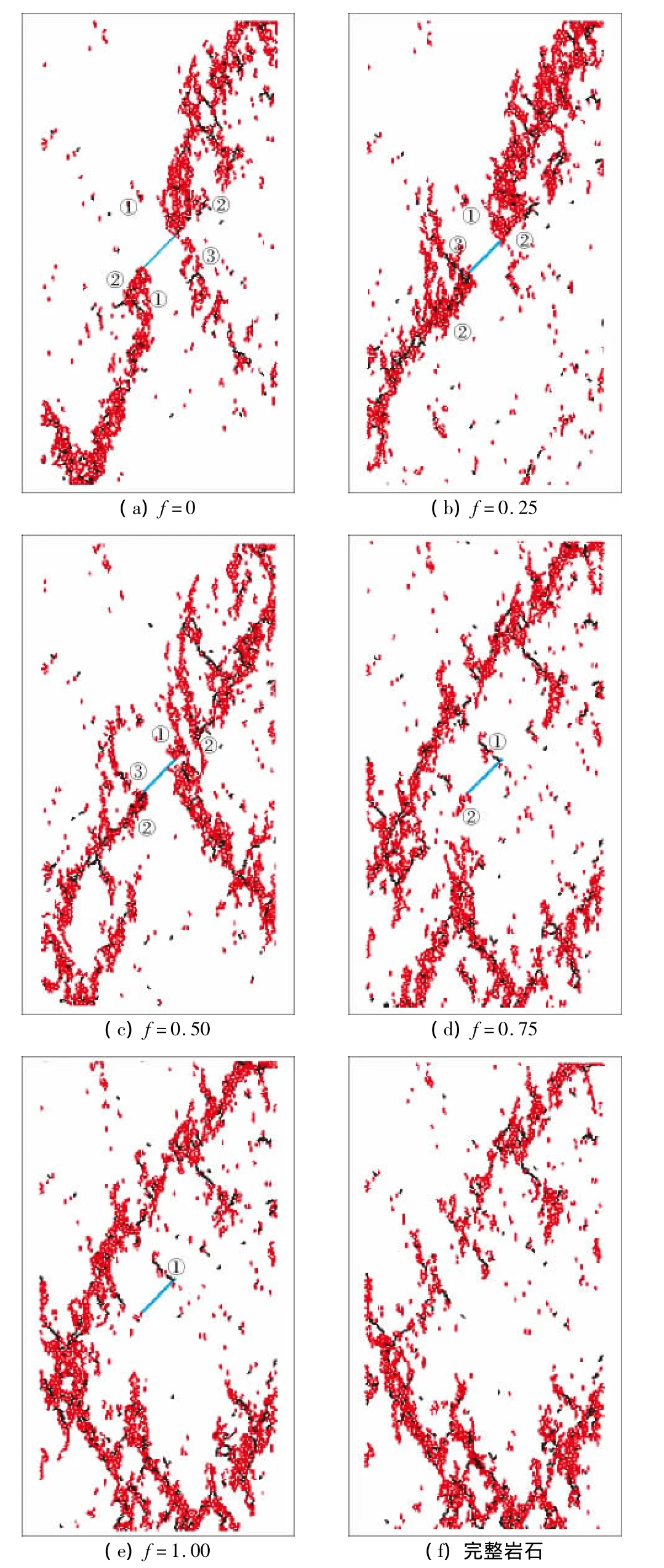
图7 不同裂隙摩擦系数下岩石破坏模式Fig.7 Failure modes of cracked rock with different fissure frictional coefficients

方案 2 中裂隙长度 2a=5，10，15，20，25 mm时，对应的峰值强度分别为52.12，51.26，47.70，39.92，34.65 MPa，而完整岩石的峰值强度为52.21 MPa。显然，随着裂隙长度的减小，裂隙岩石的峰值强度逐渐增大，直至接近完整岩石峰值强度。由此可知，裂隙只有在一定尺度范围内才对岩石的破坏特征存在明显影响。

3.3 裂隙摩擦系数对破坏特征的影响

实施方案(3)，研究裂隙摩擦系数对裂隙岩石破坏特征的影响。图7给出了不同裂隙摩擦系数下岩石的破坏模式。

从图7中可以看出，裂隙摩擦系数对裂隙岩石破坏特征存在明显影响:

(1)随着裂隙摩擦系数的增大，裂隙岩石破坏模式越来越接近于完整岩石破坏模式，当f=1时裂隙岩石破坏模式与完整岩石破坏模式几乎相同。

(2)当f=0，翼型裂纹的扩展形成了裂隙岩石的贯通破坏面(Ⅰ型断裂扩展);当f=0.25，共面次生裂纹的扩展形成了裂隙岩石的贯通破坏面(Ⅱ-Ⅰ型断裂扩展);当f=0.5，共面次生裂纹和次生斜裂纹的扩展形成了裂隙岩石的贯通破坏面(Ⅱ-Ⅰ型断裂扩展);当f=0.75，1时，预制裂隙未扩展形成贯通破坏面。

图8给出了不同裂隙摩擦系数下岩石的峰值强度。

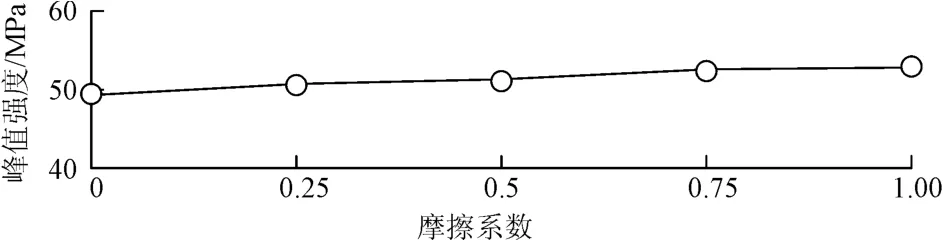
图8 不同裂隙摩擦系数下岩石峰值强度Fig.8 Peak strength of cracked rock with different fissure frictional coefficients

方案(3)中裂隙摩擦系数 f=0，0.25，0.50，0.75，1 时，对应的峰值强度分别为49.20，50.62，51.26，52.37，52.83 MPa，而完整岩石的峰值强度为52.21 MPa。显然，随着裂隙摩擦系数的增大，裂隙岩石的峰值强度逐渐增大。但是，摩擦系数对峰值强度的影响程度远不及裂隙尺度。

3.4 裂隙倾角对破坏特征的影响

实施方案(4)，研究裂隙倾角对裂隙岩石破坏特征的影响。图9给出了不同裂隙摩倾角下岩石的破坏模式。

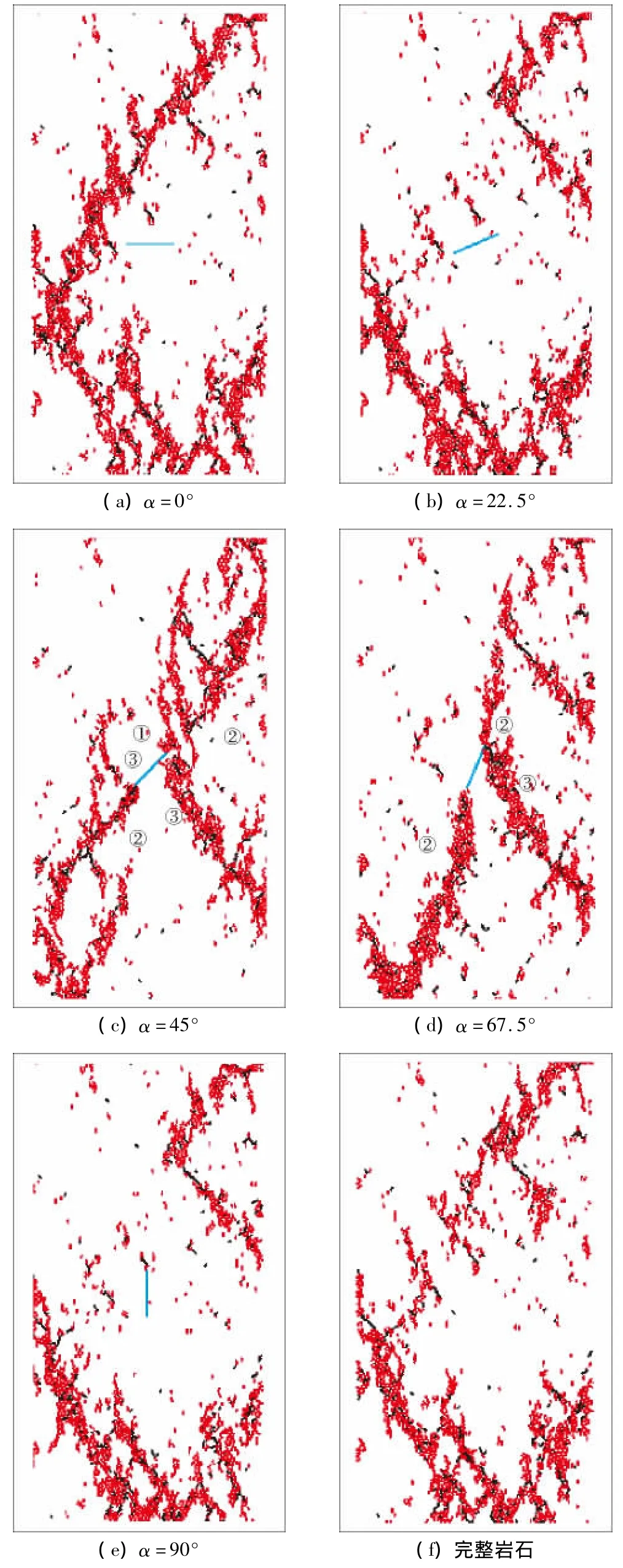
图9 不同裂隙倾角下岩石破坏模式Fig.9 Failure modes of cracked rock with different fissure dip angles

从图9中可以看出，裂隙倾角对裂隙岩石破坏特征存在明显影响:

(1)裂隙倾角 α=0°，22.5°，90°时，裂隙岩石破坏模式与完整岩石破坏模式相同。

(2)裂隙倾角α=45°时，共面次生裂纹和次生斜裂纹的扩展形成了裂隙岩石的贯通破坏面(Ⅱ-Ⅰ型断裂扩展);裂隙倾角α=67.5°时，翼型裂纹的扩展形成了裂隙岩石的贯通破坏面(Ⅰ型断裂扩展);裂隙倾角α=90°时，裂隙尖端几乎没有产生翼型裂纹。

图10给出了不同裂隙摩擦系数下岩石的峰值强度。

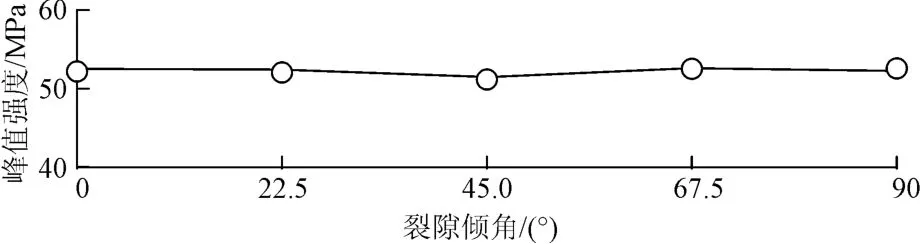
图10 不同裂隙倾角下岩石峰值强度Fig.10 Peak strength of cracked rock with different fissure dip angels

方案(4)中裂隙倾角 α=0°，22.5°，45°，67.5°，90°时，对应的峰值强度分别为52.12，52.03，51.26，52.27，52.09 MPa，而完整岩石的峰值强度为52.21 MPa。可以看出，裂隙倾角似乎对峰值强度的影响并不大，以裂隙倾角α=45°时，裂隙岩石的峰值强度最低。

4 理论分析

上述数值模拟结果显示，对于含单一闭合裂隙的岩石而言，其单轴压缩破坏特征受到裂隙长度、摩擦系数和倾角的影响。当裂隙长度越短、摩擦系数越大、倾角越接近于0°或者90°时，裂隙岩石的破坏模式和峰值强度越接近于完整岩石。下面以断裂力学理论对此进行解释。

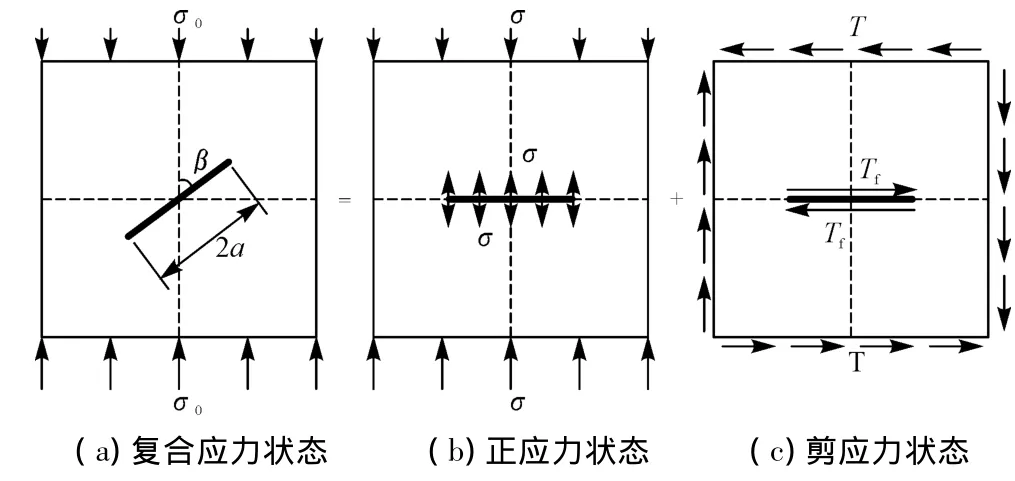
图11 闭合裂纹压剪复合应力状态应力叠加示意图Fig.11 Stress superposition of closed fissure in compression-shear condition

单轴压缩下，岩石裂隙一般处于压剪复合应力状态。根据线弹性断裂力学中的叠加原理，图11(a)所示的闭合裂隙可由图11(b)和图11(c)所示的2种加载情况叠加而成，并且满足［7］:

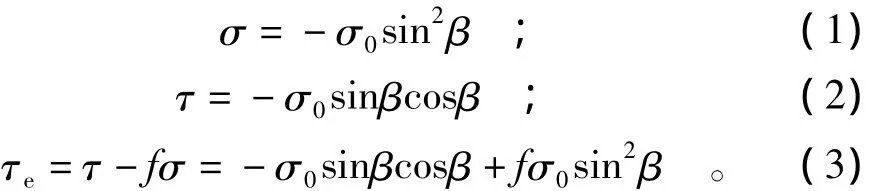
式中:采用弹性力学符号制，τe为裂纹有效剪应力;f为裂纹表面摩擦系数，当裂纹未闭合时，不考虑摩擦阻力，取f=0。

对于压剪复合应力状态，其裂隙尖端应力场与拉剪复合应力状态具有明显区别。拉剪加载下的拉应力使裂隙面具有分离趋势，而压剪加载下的压应力使裂隙面具有闭合趋势，裂隙闭合后，将会在裂隙接触面产生摩擦阻力，进一步提高了抗剪断能力［8］。考虑裂纹处于闭合状态的扩展规律，利用平面应力状态理论，将图11(b)直角坐标下的应力分量转换成极坐标下的表达式:

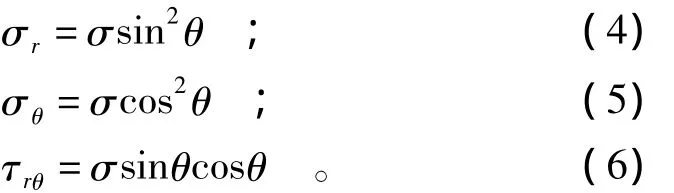
根据应力叠加原理，可以得到压剪加载下岩石裂纹尖端应力计算公式［8］为:

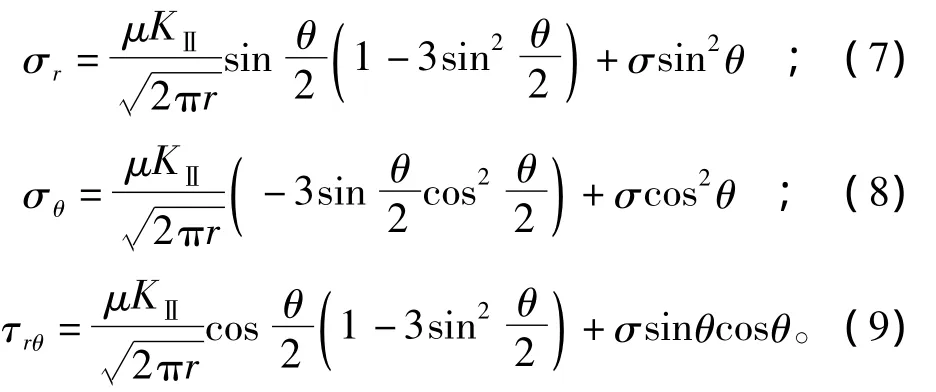
式中:KⅡ=τe为形状修正系数。

式(7)至式(9)中等式右边第2项不影响应力场的奇异性，在越靠近裂尖时，该项在应力场中所占的比例越小，因此可以忽略［8］。由此可以认为压剪条件下的闭合裂隙为特殊的纯Ⅱ型裂纹［9］。

按照最大周向应力理论，主控结构面必然沿着具有最大周向拉应力σθmax的截面扩展，假设该截面与主控结构面之间的夹角为θ0，有

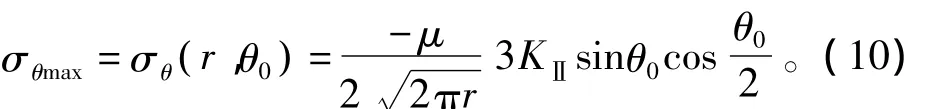
引入相当应力强度因子Ke，其表达式为

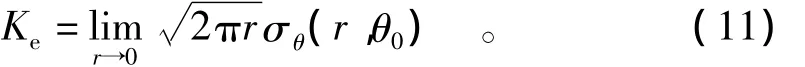
将式(11)代入式(10)可得

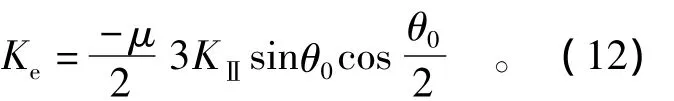
裂隙的扩展条件为

式中KIC为岩石Ⅰ型断裂韧度。

根据KⅡ=τe可知，裂隙长度越小，则|KⅡ|越小;|τe|=σ0sinβcosβ－fσ0sin2β 可知，裂隙摩擦系数越大，裂隙倾角越接近于0°或者90°时(β越接近于90°或者0°)，|τe|越小，则|KⅡ|越小。显然，|KⅡ|越小，则闭合裂隙越难产生断裂扩展，裂隙岩石破坏特征越接近于完整岩石状态。比如，当f=1，β=45°时，KⅡ=0，裂隙岩石类似完整岩石状态，即图7(e)的情况。由此，解释了裂隙长度、摩擦系数和倾角对裂隙岩石破坏特征的影响。

5 结论

(1)压剪条件下的闭合裂隙等效于纯Ⅱ型裂纹，裂隙长度越小，裂隙摩擦系数越大，裂隙倾角越接近于0°或者90°时，|KⅡ|越小，闭合裂隙越难产生断裂扩展，裂隙岩石破坏特征越接近于完整岩石状态。颗粒流数值模拟结果验证了上述观点。

(2)压缩条件下裂隙扩展一般产生3种形式的裂纹:翼型裂纹、共面次生裂纹和次生斜裂纹。翼型裂纹一般最先出现，表现为张拉破坏(Ⅰ型断裂扩展)，次生裂纹扩展之初表现为剪切破坏(Ⅱ型断裂扩展)，但随着扩展的进行，出现张拉破坏(Ⅰ型断裂扩展)。

(3)裂隙岩石的破坏一般是翼型裂纹或次生裂纹的断裂扩展最终形成岩石的贯通破坏面，其中翼型裂纹为Ⅰ型断裂扩展形成贯通破坏面，次生裂纹为Ⅱ-Ⅰ型断裂扩展形成贯通破坏面。

［1］付金伟，朱维申，王向刚，等.节理岩体裂隙扩展过程一种新改进的弹脆性模拟方法及应用［J］.岩石力学与工程学报，2012，31(10):2088－2095.(FU Jin-wei，ZHU Wei-shen，WANG Xiang-gang，et al.An Improved Elastic-brittle Simulation Method of Crack Propagation Process in Jointed Rock Mass and Its Application［J］.Chinese Journal of Rock Mechanics and Engineering，2012，31(10):2088－2095.(in Chinese))

［2］李 瑶，姚 池.含两条共面非贯通裂隙岩石的单轴压缩特性数值研究［J］.水电能源科学，2014，32(9):127－130，106.(LI Yao，YAO Chi.Numerical Simulation of Rocks Containing Two Coplanar Non-persistent Fissures under Uniaxial Compression［J］.Water Re-sources and Power，2014，32(9):127－130，106.(in Chinese))

［3］杨圣奇，黄彦华，刘相如.断续双裂隙岩石抗拉强度与裂纹扩展颗粒流分析［J］.中国矿业大学学报，2014，43(2):220－ 266.(YANG Sheng-qi，HUANG Yanhua，LIU Xiang-ru.Particle Flow Analysis on Tensile Strength and Crack Coalescence Behavior of Brittle Rock Containing Two Pre-existing Fissures［J］.Journal of China University of Mining＆ Technology，2014，43(2):220－266.(in Chinese))

［4］黄彦华，杨圣奇.非共面双裂隙红砂岩宏细观力学行为颗粒流模拟［J］.岩石力学与工程学报，2014，33(8):1644－1653.(HUANG Yan-hua，YANG Shengqi.Particle Flow Simulation of Macro and Meso-mechanical Behavior of Red Sandstone Containing Two Pre-existing Non-coplanar Fissures［J］.Chinese Journal of Rock Mechanics and Engineering，2014，33(8):1644－1653.(in Chinese))

［5］张社荣，孙 博，王 超，等.双轴压缩试验下岩石裂纹扩展的离散元分析［J］.岩石力学与工程学报，2013，32(增2):3083－ 3091.(ZHANG She-rong，SUN Bo，WANG Chao，et al.Discrete Element Analysis of Crack Propagation in Rocks under Biaxial Compression［J］.Chinese Journal of Rock Mechanics and Engineering，2013，32(Sup.2):3083－3091.(in Chinese))

［6］PARK C H，BOBET A.Crack Coalescence in Specimens with Open and Closed Flaws:A Comparison［J］.International Journal of Rock Mechanics ＆ Mining Sciences，2009，46(5):819－829.

［7］李祥龙.层状节理岩体高边坡地震动力破坏机理研究［D］.武汉:中国地质大学，2013.(LI Xiang-long.Research of the Seismic-induced Failure Mechanism of Layered Rock High Slope［D］.Wuhan:China University of Geosciences，2013.(in Chinese))

［8］陈 枫.岩石压剪断裂的理论与实验研究［D］.长沙:中南大学，2002.(CHEN Feng.Theoretical and Experimental Investigation on Rock Fracture due to Shear-Compression Loading［D］.Changsha:Central South University，2002.(in Chinese))

［9］杨 慧，曹 平，江学良，等.闭合裂纹断裂的有效剪应力准则［J］.岩土力学，2008，29(增刊):470－474.(YANG Hui，CAOPing，JIANGXue-liang，et al.Effective Shear Stress Criterion for Closed-crack Fracture［J］.Rock and Soil Mechanics，2008，29(Sup.):470－474.(in Chinese))